DOCSLIB.ORG

An Introduction to Computational Finance Without Agonizing Pain

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
An Introduction to Computational Finance Without Agonizing Pain An Introduction to Computational Finance Without Agonizing Pain c Peter Forsyth 2021 P.A. Forsyth∗ January 18, 2021 Contents 1 The First Option Trade 4 2 The Black-Scholes Equation 4 2.1 Background . 4 2.2 Definitions . 5 2.3 A Simple Example: The Two State Tree . 5 2.4 A hedging strategy . 6 2.5 Brownian Motion . 6 2.6 Geometric Brownian motion with drift . 12 2.6.1 Ito's Lemma . 14 2.6.2 Some uses of Ito's Lemma . 15 2.6.3 Some more uses of Ito's Lemma . 15 2.6.4 Integration by Parts . 17 2.7 The Black-Scholes Analysis . 17 2.8 Hedging in Continuous Time . 18 2.9 The option price . 19 2.10 American early exercise . 19 3 The Risk Neutral World 20 4 Monte Carlo Methods 22 4.1 Monte Carlo Error Estimators . 24 4.2 Random Numbers and Monte Carlo . 24 4.3 The Box-Muller Algorithm . 26 4.3.1 An improved Box Muller . 27 4.4 Speeding up Monte Carlo . 29 4.5 Estimating the mean and variance . 30 4.6 Low Discrepancy Sequences . 31 ∗Cheriton School of Computer Science, University of Waterloo, Waterloo, Ontario, Canada, N2L 3G1, [email protected], www.scicom.uwaterloo.ca/ paforsyt, tel: (519) 888-4567x34415, fax: (519) 885-1208 1 4.7 Correlated Random Numbers . 32 4.8 Integration of Stochastic Differential Equations . 34 4.8.1 The Brownian Bridge . 34 4.8.2 Strong and Weak Convergence . 36 4.9 Matlab and Monte Carlo Simulation . 38 5 The Binomial Model: Overview 41 5.1 A Binomial Model Based on the Risk Neutral Walk . 41 5.2 A No-arbitrage Lattice . 43 5.3 A Drifting Lattice . 45 5.3.1 Numerical Comparison: No-arbitrage Lattice and Drifting Lattice . 47 5.4 Smoothing the Payoff . 48 5.4.1 Richardson extrapolation . 52 5.5 Matlab Implementation . 52 5.5.1 American Case . 54 5.5.2 Discrete Fixed Amount Dividends . 55 5.5.3 Discrete Dividend Example . 56 5.6 Dynamic Programming . 57 6 More on Ito's Lemma 58 7 Derivative Contracts on non-traded Assets and Real Options 61 7.1 Derivative Contracts . 62 7.2 A Forward Contract . 65 7.2.1 Convenience Yield . 66 7.2.2 Volatility of Forward Prices . 66 8 Discrete Hedging 67 8.1 Delta Hedging . 67 8.2 Gamma Hedging . 68 8.3 Vega Hedging . 71 8.4 A Stop-Loss Strategy . 72 8.4.1 Profit and Loss: probability density, VAR and CVAR . 73 8.4.2 Another way of computing CVAR . 74 8.5 Collateralized deals . 76 8.5.1 Hedger . 76 8.5.2 Buyer B . 77 9 Jump Diffusion 78 9.1 The Poisson Process . 80 9.2 The Jump Diffusion Pricing Equation . 82 9.3 An Alternate Derivation of the Pricing Equation for Jump Diffusion . 83 9.4 Simulating Jump Diffusion . 86 9.4.1 Compensated Drift . 87 9.4.2 Contingent Claims Pricing . 88 9.5 Matlab Code: Jump Diffusion . 88 9.6 Poisson Distribution . 90 10 Regime Switching 91 2 11 Mean Variance Portfolio Optimization 92 11.1 Special Cases . 94 11.2 The Portfolio Allocation Problem . 94 11.3 Adding a Risk-free asset . 97 11.4 Criticism . 99 11.5 Individual Securities . 99 12 Some Investing Facts 103 12.1 Stocks for the Long Run? . 103 12.1.1 GBM is Risky . 105 12.2 Volatility Pumping . 107 12.2.1 Constant Proportions Strategy . 108 12.2.2 Leveraged Two Times Bull/Bear ETFs . 110 12.3 More on Volatility Pumping . 111 12.3.1 Constant Proportion Portfolio Insurance . 112 12.3.2 Covered Call Writing . 113 12.3.3 Stop Loss, Start Gain . 114 12.4 Target Date: Ineffectiveness of glide path strategies . 116 12.4.1 Extension to jump diffusion case . 120 12.4.2 Dollar cost averaging . 122 12.5 Bootstrap Resampling . 122 12.5.1 Data and Investment Portfolio . 123 12.5.2 Investment scenario . 124 12.5.3 Deterministic Strategies . 124 12.5.4 Criteria for Success . 124 12.5.5 Bootstrap results . 125 12.6 Maximizing Sharpe ratios . 125 12.6.1 Numerical Examples . 128 12.6.2 Deficiencies of mean-variance (Sharpe ratio) criteria . 130 13 Further Reading 132 13.1 General Interest . ..
Load more

Recommended publications
  • Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus
    Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus Award winning Hedge Fund is seeking to build their team with top researchers to join their offices in Limassol, Cyprus. IKOS is an investment advisor that deploys quantitative hedge fund strategies to trade the global financial markets, with a long and successful track record. This is an exciting opportunity to join a fast growing company that is focused on the development of the best research and trading infrastructure. THE ROLE We are looking for top class mathematicians to work with us in modern quantitative finance. Our researchers participate in novel financial analysis and development efforts that require significant application of mathematical modelling techniques. The position involves working within the Global Research team; there is also significant interaction with the trading and fund management teams. The objective is the development of innovative products and computational methods in the equities, futures, currency and fixed income markets. In addition, the role involves statistical analysis of portfolio risk and returns, involvement in the portfolio management process and monitoring and analysing transactions on an ongoing basis. THE INDIVIDUAL The successful candidates will have a first class degree and practical science or engineering problem solving skills through a PhD in mathematics or mathematical sciences, together with excellent all round analytical and programming abilities. The following skills are also prerequisites for the job:
    [Show full text]
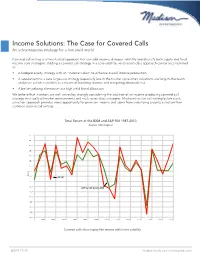
  • Income Solutions: the Case for Covered Calls an Advantageous Strategy for a Low-Yield World
    Income Solutions: The Case for Covered Calls An advantageous strategy for a low-yield world Covered call writing is a time-tested approach that can add income, dampen volatility and diversify both equity and fixed income core strategies. Adding a covered call strategy in a core-satellite, multi-asset-class approach can be accomplished as: • A hedged equity strategy with an “income kicker” to enhance overall income production • A supplement to a core large-cap strategy (especially late in the market cycle when valuations are long-in-the-tooth and price action is volatile) as a means of boosting income and mitigating downside risk • A better-yielding alternative to a high yield bond allocation We believe that investors are well-served by strongly considering the addition of an income-producing covered call strategy in virtually all market environments and multi-asset class strategies. Madison’s active call writing/active stock selection approach provides more opportunity for premium income and alpha from underlying security selection than common passive call writing. Total Return of the BXM and S&P 500 1987-2013 Rolling Returns Source: Morningstar Time Period: 1/1/1987 to 12/31/2013 Rolling Window: 1 Year 1 Year shift 40.0 35.0 30.0 25.0 20.0 15.0 10.0 5.0 Return 0.0 S&P 500 -5.0 -10.0 CBOE S&P 500 Buywrite BXM -15.0 -20.0 -25.0 -30.0 -35.0 -40.0 1989 1991 1993 1995 1997 1999 2001 2003 2005 2007 2009 2011 2013 S&P 500 TR USD Covered calls show equity-likeCBOE returns S&P 500 with Buyw ritelower BXM volatility Source: Morningstar Direct 888.971.7135 madisonfunds.com | madisonadv.com Covered Call Strategy(A) Benefits of Individual Stock Options vs.
    [Show full text]
  • Master of Science in Finance (MSF) 1
    Master of Science in Finance (MSF) 1 MASTER OF SCIENCE IN FINANCE (MSF) MSF 501 MSF 505 Mathematics with Financial Applications Futures, Options, and OTC Derivatives This course provides a systematic exposition of the primary This course provides the foundation for understanding the price mathematical methods used in financial economics. Mathematical and risk management of derivative securities. The course starts concepts and methods include logarithmic and exponential with simple derivatives, e.g., forwards and futures, and develops functions, algebra, mean-variance analysis, summations, matrix the concept of arbitrage-free pricing and hedging. Based upon algebra, differential and integral calculus, and optimization. The the work of Black, Scholes, and Merton, the course extends their course will include a variety of financial applications including pricing model through the use of lattices, Monte Carlo simulation compound interest, present and future value, term structure of methods, and more advanced strategies. Mathematical tools in interest rates, asset pricing, expected return, risk and measures stochastic processes are gradually introduced throughout the of risk aversion, capital asset pricing model (CAPM), portfolio course. Particular emphasis is given to the pricing of interest rate optimization, expected utility, and consumption capital asset pricing derivatives, e.g., FRAs, swaps, bond options, caps, collars, and (CCAPM). floors. Lecture: 3 Lab: 0 Credits: 3 Prerequisite(s): MSF 501 with min. grade of C and MSF 503 with min. grade of C and MSF 502 with min. grade of C MSF 502 Lecture: 3 Lab: 0 Credits: 3 Statistical Analysis in Financial Markets This course presents and applies statistical and econometric MSF 506 techniques useful for the analysis of financial markets.
    [Show full text]
  • Structured Products in Asia
    2015 ISSUE: NOVEMBER Structured Products in Asia hubbis.com 1st Leonteq has received more than 20 awards since its foundation in 2007 THE QUINTESSENCE OF OUR MISSION STATEMENT LET´S REDEFINE YOUR INVESTMENT EXPERIENCE Leonteq’s explicit goal is to make a difference through particular transparency in structured investment products and to be the preferred technology and service partner for investment solutions. We count on experienced industry experts with a focus on achieving client’s goals and a fi rst class IT infrastructure, setting new stand- ards in stability and fl exibility. OUR DIFFERENTIATION Modern platform • Integrated IT platform built from ground up with a focus on automation of key processes in the value chain • Platform functionality to address increased customer demand for transparency, service, liquidity, security and sustainability Vertical integration • Control of the entire value chain as a basis for proactive service tailored to specifi c needs of clients • Automation of key processes mitigating operational risks Competitive cost per issued product • Modern platform resulting in a competitive cost per issued product allowing for small ticket sizes LEGAL DISCLAIMER Leonteq Securities (Hong Kong) Limited (CE no.AVV960) (“Leonteq Hong Kong”) is responsible for the distribution of this publication in Hong Kong. It is licensed and regulated by the Hong Kong Securities and Futures Commission for Types 1 and 4 regulated activities. The services and products it provides are available only to “profes- sional investors” as defi ned in the Securities and Futures Ordinance (Cap. 571) of Hong Kong. This document is being communicated to you solely for the purposes of providing information regarding the products and services that the Leonteq group currently offers, subject to applicable laws and regulations.
    [Show full text]
  • From Arbitrage to Arbitrage-Free Implied Volatilities
    Journal of Computational Finance 20(3), 31–49 DOI: 10.21314/JCF.2016.316 Research Paper From arbitrage to arbitrage-free implied volatilities Lech A. Grzelak1,2 and Cornelis W. Oosterlee1,3 1Delft Institute of Applied Mathematics, Delft University of Technology, Mekelweg 4, 2628 CD, Delft, The Netherlands; email: [email protected] 2ING, Quantiative Analytics, Bijlmerplein 79, 1102 BH, Amsterdam, The Netherlands 3CWI: National Research Institute for Mathematics and Computer Science, Science Park 123, 1098 XG, Amsterdam, The Netherlands; email: [email protected] (Received October 14, 2015; revised March 6, 2016; accepted March 7, 2016) ABSTRACT We propose a method for determining an arbitrage-free density implied by the Hagan formula. (We use the wording “Hagan formula” as an abbreviation of the Hagan– Kumar–Le´sniewski–Woodward model.) Our method is based on the stochastic collo- cation method. The principle is to determine a few collocation points on the implied survival distribution function and project them onto the polynomial of an arbitrage- free variable for which we choose the Gaussian variable. In this way, we have equality in probability at the collocation points while the generated density is arbitrage free. Analytic European option prices are available, and the implied volatilities stay very close to those initially obtained by the Hagan formula. The proposed method is very fast and straightforward to implement, as it only involves one-dimensional Lagrange interpolation and the inversion of a linear system of equations. The method is generic and may be applied to other variants or other models that generate arbitrage. Keywords: arbitrage-free density; collocation method; orthogonal projection; arbitrage-free volatility; SCMC sampler; implied volatility parameterization.
    [Show full text]
  • Careers in Quantitative Finance by Steven E
    Careers in Quantitative Finance by Steven E. Shreve1 August 2018 1 What is Quantitative Finance? Quantitative finance as a discipline emerged in the 1980s. It is also called financial engineering, financial mathematics, mathematical finance, or, as we call it at Carnegie Mellon, computational finance. It uses the tools of mathematics, statistics, and computer science to solve problems in finance. Computational methods have become an indispensable part of the finance in- dustry. Originally, mathematical modeling played the dominant role in com- putational finance. Although this continues to be important, in recent years data science and machine learning have become more prominent. Persons working in the finance industry using mathematics, statistics and computer science have come to be known as quants. Initially relegated to peripheral roles in finance firms, quants have now taken center stage. No longer do traders make decisions based solely on instinct. Top traders rely on sophisticated mathematical models, together with analysis of the current economic and financial landscape, to guide their actions. Instead of sitting in front of monitors \following the market" and making split-second decisions, traders write algorithms that make these split- second decisions for them. Banks are eager to hire \quantitative traders" who know or are prepared to learn this craft. While trading may be the highest profile activity within financial firms, it is not the only critical function of these firms, nor is it the only place where quants can find intellectually stimulating and rewarding careers. I present below an overview of the finance industry, emphasizing areas in which quantitative skills play a role.
    [Show full text]
  • Financial Mathematics
    Financial Mathematics Alec Kercheval (Chair, Florida State University) Ronnie Sircar (Princeton University) Jim Sochacki (James Madison University) Tim Sullivan (Economics, Towson University) Introduction Financial Mathematics developed in the mid-1980s as research mathematicians became interested in problems, largely involving stochastic control, that had until then been studied primarily by economists. The subject grew slowly at first and then more rapidly from the mid- 1990s through to today as mathematicians with backgrounds first in probability and control, then partial differential equations and numerical analysis, got into it and discovered new issues and challenges. A society of mostly mathematicians and some economists, the Bachelier Finance Society, began in 1997 and holds biannual world congresses. The Society for Industrial and Applied Mathematics (SIAM) started an Activity Group in Financial Mathematics & Engineering in 2002; it now has about 800 members. The 4th SIAM conference in this area was held jointly with its annual meeting in Minneapolis in 2013, and attracted over 300 participants to the Financial Mathematics meeting. In 2009 the SIAM Journal on Financial Mathematics was launched and it has been very successful gauged by numbers of submissions. Student interest grew enormously over the same period, fueled partly by the growing financial services sector of modern economies. This growth created a demand first for quantitatively trained PhDs (typically physicists); it then fostered the creation of a large number of Master’s programs around the world, especially in Europe and in the U.S. At a number of institutions undergraduate programs have developed and become quite popular, either as majors or tracks within a mathematics major, or as joint degrees with Business or Economics.
    [Show full text]
  • Financial Engineering and Computational Finance with R Rmetrics Built 221.10065
    Rmetrics An Environment for Teaching Financial Engineering and Computational Finance with R Rmetrics Built 221.10065 Diethelm Würtz Institute for Theoretical Physics Swiss Federal Institute of Technology, ETH Zürich Rmetrics is a collection of several hundreds of functions designed and written for teaching "Financial Engineering" and "Computational Finance". Rmetrics was initiated in 1999 as an outcome of my lectures held on topics in econophysics at ETH Zürich. The family of the Rmetrics packages build on ttop of the statistical software environment R includes members dealing with the following subjects: fBasics - Markets and Basic Statistics, fCalendar - Date, Time and Calendar Management, fSeries - The Dynamical Process Behind Financial Markets, fMultivar - Multivariate Data Analysis, fExtremes - Beyond the Sample, Dealing with Extreme Values, fOptions – The Valuation of Options, and fPortfolio - Portfolio Selection and Optimization. Rmetrics has become the premier open source to download data sets from the Internet. The solution for financial market analysis and valu- major concern is given to financial return series ation of financial instruments. With hundreds of and their stylized facts. Distribution functions functions build on modern and powerful methods relevant in finance are added like the stable, the Rmetrics combines explorative data analysis and hyperbolic, or the normal inverse Gaussian statistical modeling with object oriented rapid distribution function to compute densities, pro- prototyping. Rmetrics is embedded in R, both babilities, quantiles and random deviates. Esti- building an environment which creates especially mators to fit the distributional parameters are for students and researchers in the third world a also available. Furthermore, hypothesis tests for first class system for applications in statistics and the investigation of distributional properties, of finance.
    [Show full text]
  • EQUITY DERIVATIVES Faqs
    NATIONAL INSTITUTE OF SECURITIES MARKETS SCHOOL FOR SECURITIES EDUCATION EQUITY DERIVATIVES Frequently Asked Questions (FAQs) Authors: NISM PGDM 2019-21 Batch Students: Abhilash Rathod Akash Sherry Akhilesh Krishnan Devansh Sharma Jyotsna Gupta Malaya Mohapatra Prahlad Arora Rajesh Gouda Rujuta Tamhankar Shreya Iyer Shubham Gurtu Vansh Agarwal Faculty Guide: Ritesh Nandwani, Program Director, PGDM, NISM Table of Contents Sr. Question Topic Page No No. Numbers 1 Introduction to Derivatives 1-16 2 2 Understanding Futures & Forwards 17-42 9 3 Understanding Options 43-66 20 4 Option Properties 66-90 29 5 Options Pricing & Valuation 91-95 39 6 Derivatives Applications 96-125 44 7 Options Trading Strategies 126-271 53 8 Risks involved in Derivatives trading 272-282 86 Trading, Margin requirements & 9 283-329 90 Position Limits in India 10 Clearing & Settlement in India 330-345 105 Annexures : Key Statistics & Trends - 113 1 | P a g e I. INTRODUCTION TO DERIVATIVES 1. What are Derivatives? Ans. A Derivative is a financial instrument whose value is derived from the value of an underlying asset. The underlying asset can be equity shares or index, precious metals, commodities, currencies, interest rates etc. A derivative instrument does not have any independent value. Its value is always dependent on the underlying assets. Derivatives can be used either to minimize risk (hedging) or assume risk with the expectation of some positive pay-off or reward (speculation). 2. What are some common types of Derivatives? Ans. The following are some common types of derivatives: a) Forwards b) Futures c) Options d) Swaps 3. What is Forward? A forward is a contractual agreement between two parties to buy/sell an underlying asset at a future date for a particular price that is pre‐decided on the date of contract.
    [Show full text]
  • Covered Calls Uncovered Roni Israelov and Lars N
    Financial Analysts Journal Volume 71 · Number 6 ©2015 CFA Institute Covered Calls Uncovered Roni Israelov and Lars N. Nielsen Typical covered call strategies collect the equity and volatility risk premiums but also embed exposure to a naive equity reversal strategy that is uncompensated. This article presents a novel risk and performance attribu- tion methodology that deconstructs the strategy into these three exposures. Historically, the equity exposure contributed most of the risk and return. The short volatility exposure realized a Sharpe ratio of nearly 1.0 but contributed only 10% of the risk. The equity reversal exposure contributed approximately 25% of the risk but provided little return in exchange. The authors propose a risk-managed covered call strategy that eliminates the uncompensated equity reversal exposure. This modified covered call strategy has a superior Sharpe ratio, reduced volatility, and reduced downside equity beta. quity index covered calls are the most easily by natural buyers can lead to a risk premium. accessible source of the volatility risk pre- Litterman (2011) suggested that long-term inves- Emium for most investors.1 The volatility risk tors, such as pensions and endowments, should be premium, which is absent from most investors’ port- natural providers of financial insurance and sellers folios, has had more than double the risk-adjusted of options. returns (Sharpe ratio) of the equity risk premium, Yet, many investors remain skeptical of covered which is the dominant source of return for most call strategies. Although deceptively simple—long investors. By providing the equity and volatility equity and short a call option—covered calls are not risk premiums, equity index covered calls’ returns well understood.
    [Show full text]
  • S&P/TSX 60 Covered Call Indices Methodology
    S&P/TSX 60 Covered Call Indices Methodology April 2021 S&P Dow Jones Indices: Index Methodology Table of Contents Introduction 2 Index Objective 2 Index Series 2 Supporting Documents 2 Index Construction 3 Approaches 3 Pricing 3 Index Calculations 3 Currency of Calculation and Additional Index Return Series 5 Base Date and History Availability 5 Index Governance 6 Index Committee 6 Index Policy 7 Announcements 7 Holiday Schedule 7 Unexpected Exchange Closures 7 Recalculation Policy 7 Contact Information 7 Index Dissemination 8 Index Data 8 Web site 8 Appendix: Adjustment for Corporate Actions 9 Special Dividends 9 Disclaimer 11 S&P Dow Jones Indices: S&P/TSX 60 Covered Call Indices Methodology 1 Introduction Index Objective The S&P/TSX 60 Covered Call Indices measures the performance of a strategy that writes covered calls on the iShares S&P/TSX 60 Index ETF (TSX:XIU). Index Series The index series consists of the following indices: Rebalancing Target Option Moneyness Index Frequency Moneyness Multiplier (m) S&P/TSX 60 Covered Call 2% OTM Monthly 2% OTM 1.02 Monthly Index (CAD) TR S&P/TSX 60 Covered Call 2% OTM Quarterly 2% OTM 1.02 Quarterly Index (CAD) TR Supporting Documents This methodology is meant to be read in conjunction with supporting documents providing greater detail with respect to the policies, procedures and calculations described herein. References throughout the methodology direct the reader to the relevant supporting document for further information on a specific topic. The list of the main supplemental documents for
    [Show full text]
  • Covered Call Strategies: One Fact and Eight Myths Roni Israelov and Lars N
    Financial Analysts Journal Volume 70 · Number 6 ©2014 CFA Institute PERSPECTIVES Covered Call Strategies: One Fact and Eight Myths Roni Israelov and Lars N. Nielsen A covered call is a long position in a security and a short position in a call option on that security. Equity index covered calls are an attractive strategy to many investors because they have realized returns not much lower than those of the equity market but with much lower volatility. However, a number of myths about the strategy—from why it works to why an investor should or should not invest—have surfaced, and many of them are erroneously considered “common knowledge.” The authors review the underlying risk and returns of covered call strategies and dispel eight common myths about them. covered call is a combination of a long posi- For obvious reasons, strategies that may offer tion in a security and a short position in a call equity-like expected returns but with lower volatility A option on the same security. The combined and market exposure (beta) generate strong investor position caps the investor’s upside on the underlying interest. As a case in point, covered call strategies security at the option’s strike price in exchange for have been gaining popularity: Growth in assets under an option premium. Figure 1 shows the covered call management in covered call strategies has been over payoff diagram, including the option premium, at 25% per year over the past 10 years (through June expiration when the call option is written at a $100 2014), with over $45 billion currently invested.2 strike with a $25 option premium.
    [Show full text]