Fluvial Apophenia
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Task-Based Taxonomy of Cognitive Biases for Information Visualization
A Task-based Taxonomy of Cognitive Biases for Information Visualization Evanthia Dimara, Steven Franconeri, Catherine Plaisant, Anastasia Bezerianos, and Pierre Dragicevic Three kinds of limitations The Computer The Display 2 Three kinds of limitations The Computer The Display The Human 3 Three kinds of limitations: humans • Human vision ️ has limitations • Human reasoning 易 has limitations The Human 4 ️Perceptual bias Magnitude estimation 5 ️Perceptual bias Magnitude estimation Color perception 6 易 Cognitive bias Behaviors when humans consistently behave irrationally Pohl’s criteria distilled: • Are predictable and consistent • People are unaware they’re doing them • Are not misunderstandings 7 Ambiguity effect, Anchoring or focalism, Anthropocentric thinking, Anthropomorphism or personification, Attentional bias, Attribute substitution, Automation bias, Availability heuristic, Availability cascade, Backfire effect, Bandwagon effect, Base rate fallacy or Base rate neglect, Belief bias, Ben Franklin effect, Berkson's paradox, Bias blind spot, Choice-supportive bias, Clustering illusion, Compassion fade, Confirmation bias, Congruence bias, Conjunction fallacy, Conservatism (belief revision), Continued influence effect, Contrast effect, Courtesy bias, Curse of knowledge, Declinism, Decoy effect, Default effect, Denomination effect, Disposition effect, Distinction bias, Dread aversion, Dunning–Kruger effect, Duration neglect, Empathy gap, End-of-history illusion, Endowment effect, Exaggerated expectation, Experimenter's or expectation bias, -

The Being of Analogy Noah Roderick Noah Roderick the Being of Analogy
Noah Roderick The Being of Analogy Noah Roderick Noah Roderick The Being of Analogy The Being of Modern physics replaced the dualism of matter and form with a new distinction between matter and force. In this way form was marginalized, and with it the related notion of the object. Noah Roderick’s book is a refreshing effort to reverse the consequences of this now banal mainstream materialism. Ranging from physics through literature to linguistics, spanning philosophy from East to West, and weaving it all together in remarkably lucid prose, Roderick intro- duces a new concept of analogy that sheds unfamiliar light on such thinkers as Marx, Deleuze, Goodman, Sellars, and Foucault. More than a literary device, analogy teaches us something about being itself. OPEN HUMANITIES PRESS Cover design by Katherine Gillieson · Illustration by Tammy Lu The Being of Analogy New Metaphysics Series Editors: Graham Harman and Bruno Latour The world is due for a resurgence of original speculative metaphysics. The New Metaphys- ics series aims to provide a safe house for such thinking amidst the demoralizing caution and prudence of professional academic philosophy. We do not aim to bridge the analytic- continental divide, since we are equally impatient with nail-filing analytic critique and the continental reverence for dusty textual monuments. We favor instead the spirit of the intel- lectual gambler, and wish to discover and promote authors who meet this description. Like an emergent recording company, what we seek are traces of a new metaphysical ‘sound’ from any nation of the world. The editors are open to translations of neglected metaphysical classics, and will consider secondary works of especial force and daring. -

The Art of Thinking Clearly
For Sabine The Art of Thinking Clearly Rolf Dobelli www.sceptrebooks.co.uk First published in Great Britain in 2013 by Sceptre An imprint of Hodder & Stoughton An Hachette UK company 1 Copyright © Rolf Dobelli 2013 The right of Rolf Dobelli to be identified as the Author of the Work has been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means without the prior written permission of the publisher, nor be otherwise circulated in any form of binding or cover other than that in which it is published and without a similar condition being imposed on the subsequent purchaser. A CIP catalogue record for this title is available from the British Library. eBook ISBN 978 1 444 75955 6 Hardback ISBN 978 1 444 75954 9 Hodder & Stoughton Ltd 338 Euston Road London NW1 3BH www.sceptrebooks.co.uk CONTENTS Introduction 1 WHY YOU SHOULD VISIT CEMETERIES: Survivorship Bias 2 DOES HARVARD MAKE YOU SMARTER?: Swimmer’s Body Illusion 3 WHY YOU SEE SHAPES IN THE CLOUDS: Clustering Illusion 4 IF 50 MILLION PEOPLE SAY SOMETHING FOOLISH, IT IS STILL FOOLISH: Social Proof 5 WHY YOU SHOULD FORGET THE PAST: Sunk Cost Fallacy 6 DON’T ACCEPT FREE DRINKS: Reciprocity 7 BEWARE THE ‘SPECIAL CASE’: Confirmation Bias (Part 1) 8 MURDER YOUR DARLINGS: Confirmation Bias (Part 2) 9 DON’T BOW TO AUTHORITY: Authority Bias 10 LEAVE YOUR SUPERMODEL FRIENDS AT HOME: Contrast Effect 11 WHY WE PREFER A WRONG MAP TO NO -

Communication Science to the Public
David M. Berube North Carolina State University ▪ HOW WE COMMUNICATE. In The Age of American Unreason, Jacoby posited that it trickled down from the top, fueled by faux-populist politicians striving to make themselves sound approachable rather than smart. (Jacoby, 2008). EX: The average length of a sound bite by a presidential candidate in 1968 was 42.3 seconds. Two decades later, it was 9.8 seconds. Today, it’s just a touch over seven seconds and well on its way to being supplanted by 140/280- character Twitter bursts. ▪ DATA FRAMING. ▪ When asked if they truly believe what scientists tell them, NEW ANTI- only 36 percent of respondents said yes. Just 12 percent expressed strong confidence in the press to accurately INTELLECTUALISM: report scientific findings. ▪ ROLE OF THE PUBLIC. A study by two Princeton University researchers, Martin TRENDS Gilens and Benjamin Page, released Fall 2014, tracked 1,800 U.S. policy changes between 1981 and 2002, and compared the outcome with the expressed preferences of median- income Americans, the affluent, business interests and powerful lobbies. They concluded that average citizens “have little or no independent influence” on policy in the U.S., while the rich and their hired mouthpieces routinely get their way. “The majority does not rule,” they wrote. ▪ Anti-intellectualism and suspicion (trends). ▪ Trump world – outsiders/insiders. ▪ Erasing/re-writing history – damnatio memoriae. ▪ False news. ▪ Infoxication (CC) and infobesity. ▪ Aggregators and managed reality. ▪ Affirmation and confirmation bias. ▪ Negotiating reality. ▪ New tribalism is mostly ideational not political. ▪ Unspoken – guns, birth control, sexual harassment, race… “The amount of technical information is doubling every two years. -

Aesthetics After Finitude Anamnesis Anamnesis Means Remembrance Or Reminiscence, the Collection and Re- Collection of What Has Been Lost, Forgotten, Or Effaced
Aesthetics After Finitude Anamnesis Anamnesis means remembrance or reminiscence, the collection and re- collection of what has been lost, forgotten, or effaced. It is therefore a matter of the very old, of what has made us who we are. But anamnesis is also a work that transforms its subject, always producing something new. To recollect the old, to produce the new: that is the task of Anamnesis. a re.press series Aesthetics After Finitude Baylee Brits, Prudence Gibson and Amy Ireland, editors re.press Melbourne 2016 re.press PO Box 40, Prahran, 3181, Melbourne, Australia http://www.re-press.org © the individual contributors and re.press 2016 This work is ‘Open Access’, published under a creative commons license which means that you are free to copy, distribute, display, and perform the work as long as you clearly attribute the work to the authors, that you do not use this work for any commercial gain in any form whatso- ever and that you in no way alter, transform or build on the work outside of its use in normal aca- demic scholarship without express permission of the author (or their executors) and the publisher of this volume. For any reuse or distribution, you must make clear to others the license terms of this work. For more information see the details of the creative commons licence at this website: http://creativecommons.org/licenses/by-nc-nd/2.5/ National Library of Australia Cataloguing-in-Publication Data Title: Aesthetics after finitude / Baylee Brits, Prudence Gibson and Amy Ireland, editors. ISBN: 9780980819793 (paperback) Series: Anamnesis Subjects: Aesthetics. -
Infographic I.10
The Digital Health Revolution: Leaving No One Behind The global AI in healthcare market is growing fast, with an expected increase from $4.9 billion in 2020 to $45.2 billion by 2026. There are new solutions introduced every day that address all areas: from clinical care and diagnosis, to remote patient monitoring to EHR support, and beyond. But, AI is still relatively new to the industry, and it can be difficult to determine which solutions can actually make a difference in care delivery and business operations. 59 Jan 2021 % of Americans believe returning Jan-June 2019 to pre-coronavirus life poses a risk to health and well being. 11 41 % % ...expect it will take at least 6 The pandemic has greatly increased the 65 months before things get number of US adults reporting depression % back to normal (updated April and/or anxiety.5 2021).4 Up to of consumers now interested in telehealth going forward. $250B 76 57% of providers view telehealth more of current US healthcare spend % favorably than they did before COVID-19.7 could potentially be virtualized.6 The dramatic increase in of Medicare primary care visits the conducted through 90% $3.5T telehealth has shown longevity, with rates in annual U.S. health expenditures are for people with chronic and mental health conditions. since April 2020 0.1 43.5 leveling off % % Most of these can be prevented by simple around 30%.8 lifestyle changes and regular health screenings9 Feb. 2020 Apr. 2020 OCCAM’S RAZOR • CONJUNCTION FALLACY • DELMORE EFFECT • LAW OF TRIVIALITY • COGNITIVE FLUENCY • BELIEF BIAS • INFORMATION BIAS Digital health ecosystems are transforming• AMBIGUITY BIAS • STATUS medicineQUO BIAS • SOCIAL COMPARISONfrom BIASa rea• DECOYctive EFFECT • REACTANCEdiscipline, • REVERSE PSYCHOLOGY • SYSTEM JUSTIFICATION • BACKFIRE EFFECT • ENDOWMENT EFFECT • PROCESSING DIFFICULTY EFFECT • PSEUDOCERTAINTY EFFECT • DISPOSITION becoming precise, preventive,EFFECT • ZERO-RISK personalized, BIAS • UNIT BIAS • IKEA EFFECT and • LOSS AVERSION participatory. -

John Collins, President, Forensic Foundations Group
On Bias in Forensic Science National Commission on Forensic Science – May 12, 2014 56-year-old Vatsala Thakkar was a doctor in India but took a job as a convenience store cashier to help pay family expenses. She was stabbed to death outside her store trying to thwart a theft in November 2008. Bloody Footwear Impression Bloody Tire Impression What was the threat? 1. We failed to ask ourselves if this was a footwear impression. 2. The appearance of the impression combined with the investigator’s interpretation created prejudice. The accuracy of our analysis became threatened by our prejudice. Types of Cognitive Bias Available at: http://en.wikipedia.org/wiki/List_of_cognitive_biases | Accessed on April 14, 2014 Anchoring or focalism Hindsight bias Pseudocertainty effect Illusory superiority Levels-of-processing effect Attentional bias Hostile media effect Reactance Ingroup bias List-length effect Availability heuristic Hot-hand fallacy Reactive devaluation Just-world phenomenon Misinformation effect Availability cascade Hyperbolic discounting Recency illusion Moral luck Modality effect Backfire effect Identifiable victim effect Restraint bias Naive cynicism Mood-congruent memory bias Bandwagon effect Illusion of control Rhyme as reason effect Naïve realism Next-in-line effect Base rate fallacy or base rate neglect Illusion of validity Risk compensation / Peltzman effect Outgroup homogeneity bias Part-list cueing effect Belief bias Illusory correlation Selective perception Projection bias Peak-end rule Bias blind spot Impact bias Semmelweis -

Mitigating the Attraction Effect with Visualizations Evanthia Dimara, Gilles Bailly, Anastasia Bezerianos, Steven Franconeri
Mitigating the Attraction Effect with Visualizations Evanthia Dimara, Gilles Bailly, Anastasia Bezerianos, Steven Franconeri To cite this version: Evanthia Dimara, Gilles Bailly, Anastasia Bezerianos, Steven Franconeri. Mitigating the Attrac- tion Effect with Visualizations. IEEE Transactions on Visualization and Computer Graphics, Insti- tute of Electrical and Electronics Engineers, 2019, TVCG 2019 (InfoVis 2018), 25 (1), pp.850 - 860. 10.1109/TVCG.2018.2865233. hal-01845004v2 HAL Id: hal-01845004 https://hal.inria.fr/hal-01845004v2 Submitted on 22 Aug 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TVCG.2018.2865233, IEEE Transactions on Visualization and Computer Graphics Mitigating the Attraction Effect with Visualizations Evanthia Dimara, Gilles Bailly, Anastasia Bezerianos, and Steven Franconeri Abstract—Human decisions are prone to biases, and this is no less true for decisions made within data visualizations. Bias mitigation strategies often focus on the person, by educating people about their biases, typically with little success. We focus instead on the system, presenting the first evidence that altering the design of an interactive visualization tool can mitigate a strong bias – the attraction effect. -

How a Machine Learns and Fails 2019
Repositorium für die Medienwissenschaft Matteo Pasquinelli How a Machine Learns and Fails 2019 https://doi.org/10.25969/mediarep/13490 Veröffentlichungsversion / published version Zeitschriftenartikel / journal article Empfohlene Zitierung / Suggested Citation: Pasquinelli, Matteo: How a Machine Learns and Fails. In: spheres: Journal for Digital Cultures. Spectres of AI (2019), Nr. 5, S. 1–17. DOI: https://doi.org/10.25969/mediarep/13490. Erstmalig hier erschienen / Initial publication here: https://spheres-journal.org/wp-content/uploads/spheres-5_Pasquinelli.pdf Nutzungsbedingungen: Terms of use: Dieser Text wird unter einer Creative Commons - This document is made available under a creative commons - Namensnennung - Nicht kommerziell - Keine Bearbeitungen 4.0/ Attribution - Non Commercial - No Derivatives 4.0/ License. For Lizenz zur Verfügung gestellt. Nähere Auskünfte zu dieser Lizenz more information see: finden Sie hier: http://creativecommons.org/licenses/by-nc-nd/4.0/ http://creativecommons.org/licenses/by-nc-nd/4.0/ © the author(s) 2019 www.spheres-journal.org ISSN 2363-8621 #5 Spectres of AI sadfasdf MATTEO PASQUINELLI HOW A MACHINE LEARNS AND FAILS – A GRAMMAR OF ERROR FOR ARTIFICIAL INTELLIGENCE “Once the characteristic numbers are established for most concepts, mankind will then possess a new instrument which will enhance the capabilities of the mind to a far greater extent than optical instruments strengthen the eyes, and will supersede the microscope and telescope to the same extent that reason is superior to eyesight.”1 — Gottfried Wilhelm Leibniz. “The Enlightenment was […] not about consensus, it was not about systematic unity, and it was not about the deployment of instrumental reason: what was developed in the Enlightenment was a modern idea of truth defined by error, a modern idea of knowledge defined by failure, conflict, and risk, but also hope.”2 — David Bates. -
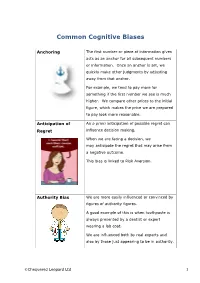
Common Cognitive Biases
Common Cognitive Biases Anchoring The first number or piece of information given acts as an anchor for all subsequent numbers or information. Once an anchor is set, we quickly make other judgments by adjusting away from that anchor. For example, we tend to pay more for something if the first number we see is much higher. We compare other prices to the initial figure, which makes the price we are prepared to pay look more reasonable. Anticipation of An a priori anticipation of possible regret can Regret influence decision making. When we are facing a decision, we may anticipate the regret that may arise from a negative outcome. This bias is linked to Risk Aversion. Authority Bias We are more easily influenced or convinced by figures of authority figures. A good example of this is when toothpaste is always presented by a dentist or expert wearing a lab coat. We are influenced both by real experts and also by those just appearing to be in authority. ãChequered Leopard Ltd 1 Choice Overload When we are given too many choices, we either prefer the default option or we avoid making any decision at all. As the number of options increases, our level of certainty about our choice decreases. Additionally, the anticipation that we will regret our choice increases.” When we are tired, we tend to conserve our energy by making choices based on a single factor like price, for example, rather than considering all the other determinants that go into making the best decision. Clustering Illusion We are naturally pattern-seeking because it helps speed up the process recognising people and things. -

1 Embrace Your Cognitive Bias
1 Embrace Your Cognitive Bias http://blog.beaufortes.com/2007/06/embrace-your-co.html Cognitive Biases are distortions in the way humans see things in comparison to the purely logical way that mathematics, economics, and yes even project management would have us look at things. The problem is not that we have them… most of them are wired deep into our brains following millions of years of evolution. The problem is that we don’t know about them, and consequently don’t take them into account when we have to make important decisions. (This area is so important that Daniel Kahneman won a Nobel Prize in 2002 for work tying non-rational decision making, and cognitive bias, to mainstream economics) People don’t behave rationally, they have emotions, they can be inspired, they have cognitive bias! Tying that into how we run projects (project leadership as a compliment to project management) can produce results you wouldn’t believe. You have to know about them to guard against them, or use them (but that’s another article)... So let’s get more specific. After the jump, let me show you a great list of cognitive biases. I’ll bet that there are at least a few that you haven’t heard of before! Decision making and behavioral biases Bandwagon effect — the tendency to do (or believe) things because many other people do (or believe) the same. Related to groupthink, herd behaviour, and manias. Bias blind spot — the tendency not to compensate for one’s own cognitive biases. Choice-supportive bias — the tendency to remember one’s choices as better than they actually were. -

Common Types of Biases and How to Mitigate Them Appendix to “Unconscious Biases Impacting Your Business” by Omar Khan, Senior Manager
Common Types of Biases and How to Mitigate Them Appendix to “Unconscious Biases Impacting Your Business” by Omar Khan, Senior Manager Anchoring Problem: Anchoring is a well-known bias where an initial piece of information can change how we perceive something. We often see it exploited in negotiations and marketing. Anchors can be completely arbitrary (e.g., a unrelated number like your SSN) or just a decoy choice (also known as a dominated option, click here for an example starting just after the 11 minute mark). Example: The exploitation of anchoring happens all around us all the time as described in the video referenced above. In the business world, anchoring often presents itself in business cases where we are influenced by things that aren’t related to the actual decision needing to be made, like if you’re making a choice between two pieces of software and there is a reference to a third piece of software that is not being considered (effectively a decoy option). Similarly, there are a lot of things you never pay list price for, but vendors will be quick to include this theoretical cost on the invoice (for example, showing you that the list price value of the software you’re getting is $1,000,000, but you’re also getting a discount of $900,000, so you only pay 1/10 the list price). In these cases, the realness of the list price needs to be considered, as does the contractual language, for renewal purposes. On performance reviews, it is easy for employees to self-assess to the highest rating possible and thus influence you into limiting your assessment into the highest rating and the rating just below that as options.