DOCSLIB.ORG

Pathways and Networks Biological Meaning of the Gene Sets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pathways and Networks Biological Meaning of the Gene Sets Pathways and Networks Biological meaning of the gene sets Gene ontology terms ? Pathway mapping Linking to Pubmed abstracts or associted MESH terms Regulation by the same transcription factor (module) Protein families and domains Gene set enrichment analysis Over representation analysis 1 Gene set enrichment analysis 1. Given an a priori defined set of genes S. 2. Rank genes (e.g. by t‐value between 2 groups of microarray samples) ranked gene list L. 3. Calculation of an enrichment score (ES) that reflects the degree to which a set S is overrepresented at the extremes (top or bottom) of the entire ranked list L. 4. Estimation the statistical significance (nominal P value) of the ES by using an empirical phenotype‐based permutation test procedure. 5. Adjustment for multiple hypothesis testing by controlling the false discovery rate (FDR). Gene set enrichment analysis Subramanian A et al. Proc Natl Acad Sci (2005) 2 Biochemical and Metabolic Pathways Böhringer Mannheim Signaling networks (in cancer cell) Hannah, Weinberg, Cell. 2000 137 NCI curated pathway maps (http://pid.nci.nih.gov) Signal Transduction Knowledge Environment http://stke.sciencemag.org/cm/ 3 Pathways • Pathways are available mechanistic information •Kyoto Encylopedia of Genes and Genomes, KEGG (http://www.genome.jp/kegg/) BioCYc • EcoCYC Metabolic Pathway Database (E. Coli) •Also for other organisms (e.g. HumanCYC) 4 Pathways • Pathways from Biocarta • http://www.biocarta.com/genes/index.asp Transpath Part of larger BioBase package (commercial) • PathwayBuilder package for network visualization • Highly integrated with signaling networks and transcription factor networks (TransFAC) • Linked to extensive enzyme information in BRENDA (www.brenda.uni‐koeln.de) • 28,456 molecules; 52,007 reactions; 54 handdrawn pathways 5 Reactome • Curated pathway database • http://www.reactome.org/ Pathway Commons • Aim: convenient access to pathway information • Facilitate creation and communication of pathway data • Aggregate pathway data in the public domain • Provide easy access for pathway analysis 6 Cytoscape • Access pathway commons from cytoscape • http://www.cytoscape.org • Open source software for network visualization • Active community • >40 plugins extend functionality e.g. Bingo, ClueGO (for gene ontology) • Easy to use and good documentation VizMapper Various layout Cline MS et al Nat Protoc. 2007 Map gene expression to pathways • GenMAPP, Cytoscape, Pathway Explorer 7 Concepts for network analysis • Pairwise similarity measures • Connection strength (adjacency functions) •Network modules (measures of node dissimilarity): • Connectivity and scale‐free network topolgy •Network motifs Similarity measures Correlation coefficient Partial correlation 8 Mutual information Discrete data Continuous data Gene co‐expression networks Expression profiles Selected genes: •abs(log2ratios)>1 in at least 5 conditions • association with metabolic pathways identified by GO analysis 9 Gene co‐expression networks 67 conditions 548 genes P Charoentong Subnetworks for insulin signaling P Charoentong 10 Gene association network MICO • Discretizing expression profiles → groups of genes with idencal profile • REVEAL algorithm based on Mutual information M(x,y)=I(x)+I(y)‐I(x,y) Pparg M(x,y)=I(x) → directed • Correlation Apmap Bogner‐Strauss et al. Cell Mol Life Sci. 2010 Adjacency function unweighted weighted 11 Topological overlap matrix (TOM) Hierarchical clustering of modules (subnetworks) Finding active subnetworks Discovering regulatory and signaling circuits in molecular interaction networks Ideker T, Ozier O, Schwikowski B, Siegel AF. Bioinformatics 18:S233‐S240 (2002) Aggregate z‐score for an entire subnetwork A of k genes: 1 ZA Zi k iA 12 Calibrating z against background distribution Randomly sample gene sets of size k using a Monte Carlo approach, compute their scores zA, and calculate standard deviation parameters for each k. Z A k Corrected subnet score S A k SA Za Z Z Z b c d ZA Scoring over multiple conditions Finding the probability that at least j of the m conditions had scores above ZA(j) 13 Finding the maximal scoring connected subgraph Simulated annealing Global maxima Local maxima Local maxima significance score subnetwork Reverse Engineering Complex System (unknown) + + - + - 14 Reverse Engineering Input Temporal series of data System Modeling Input Reverse Temporal Engineering series of data General assumption The most effective regulation acts at transcription level and is due to protein‐gene interaction. Since proteins are not measured, mRNAs is implicitly considered somehow proportional to proteins concentration proteins genes “gene-corresponding protein(s)” elements - B B - Y R incorrect - - + B real + - R - Y Y R + Gene-protein network ex. of post-transcription regulation Genomic network Correct genomic network 15 Predictive vs inferential power Techniques can have a good predictive power but a low inferential power…. Anyway we can (hopefully) identify the main involved genes - An arrow has not necessarily the meaning of a direct regulation + - Gene network Results need to be validated by using other experiments General Model Assumptions Model’s parameters are static (it is the concentration of genes and proteins that changes in time) w21 - x1 x2 The control is usually supposed instantaneous or synchronous with time delay t (number of timepoints is limited) 3 x1 x2 2 1 x1(t) x2(t) 0 024 681012 Instantaneous model -1 -2 -3 3 x1 2 x2 x1(t) x2(t+1) 1 0 Synchronous model 02468101214 -1 -2 -3 16 General Model Constraints The network must be stable: to tend to an equilibrium situation, i.e. to a static or to a cyclic condition after some time from a perturbation + Network forbidden in absence of other + connections (mRNAs and proteins in a cell can not augment indefinitely) + Boolean Networks Starting from “direct” engineering: cdk7 cyclin H cdk7 111 100 010 000 cdk7 AND cyclin H = cdk2 cdk7 cdk2 cyclin H 17 Boolean networks for sensitivity/robustness analysis CellNetAnalyzer Klemt A et al. BMC Systems Biology. 2007 Differential equation model The effect on a gene (expression level or its derivative) is modeled as a linear combination (weighted sum) of other expression levels. Naïve Example Starting from “direct” engineering: x (t 1) w x (t) w x (t) w x (t) w31 3 31 1 32 2 33 3 x1 + w 0 x3 31 - w 0 x 32 2 w32 w 33 0 18 Differential equations dx t N K i R f w x t v u t B λ x t i ij j ik k i i i dt j1 k1 Activation constant gene i Control strength of External input and their Gene i degradation law gene j on gene i control strength on i Activation function of gene i Gene j expression level 20 15 Gene i basal 10 5 activation level 0 -10 -5 0 5 10 Linear f(.) -5 -10 -15 1 0.5 Sigmoidal f(.) 0 -10 -5 0 5 10 Parameter identification • For each gene: m equations (m=time points) in n (+c) unknown parameters. • m<n undetermined problem time arrays Equation system for gene 1: x ... ... ... x 11 1m x 11 (t ) R i f w 1111 x (t ) ... w 1nn1 x (t ) λ 111x(t) ... x (t ) R f w x (t ) ... w x (t ) λ x(t) ... 12 i 1112 1nn2 112 genes ... ... xn1 ... ... ... x nm x 1m (t ) R i f w 111m x (t ) ... w 1nnm x (t ) λ 11mx(t) • Strategies: Re‐sampling + LS, SVD, simulated annealing, genetic algorithms, gradient descent 19 Bayesian networks • A Bayesian network provides not just the network, but the probability of this network to be true according to: – given data – some a priori knowledge • Components: – Acyclic Graph (main disadvantage) Nodes = Random variables to study Connections = Relation of conditional dependence among variables – Conditional Probability Distribution Assumptions and basic definitions p(G1,G2,G3,G4,G5)=p(G1)p(G2|G1)p(G3|G1)p(G4|G2)p(G5|G1,G2,G3) n p(x1,x2,…,xn) = П p(xi|pa(xi)) i=1 20 Conditional independence Serial connection p(x,y,z) = p(y)p(x|y)p(z|y) X Y Z p(z|x) = ∑ p(y|x)p(z|y) y Diverging connection Y p(x,y,z) = p(y)p(x|y)p(z|y) p(z|x) = ∑ p(y)p(x|y)p(z|y) X Z y Converging connection X Z p(x,y,z) = p(x)p(z)p(y|x,z) p(z|x) = p(z) indp. of x Y Problem to be solved max S(G|D) G D={d1,…,dm}, m is the number of samples and dl={dl1,…,dln} l є {1,…,m} and 1,…,n genes in the network. S(G|D) is a score function that measures how likely is that the data comes from every one of the networks proposed for the given nodes (genes). G is the set of all the available networks for a given set of nodes (genes). 21 Score function • Bayesian Score A priori probability P(D|G)P(G) of the network S(G|D) = P(D) Constant across the networks m n l l max (S(G|D)=ППP(d i|pa(d )) l=1 i=1 Discrete (multinomial) Continuous (Gaussian) Finding the parameters of the proposed probability function that maximizes the score function. • Minimum length Different network representation 22 Different levels of networks Network measures • Degree ki •Degree distribution P(k) •Mean path length •Network Diameter • Clustering Coefficient 23 Network measures Connectivity (degree) Clustering coefficient Topological overlap Graphs •Graph G=(V,E) is a set of vertices V and edges E where |V|=n, |E|=m the number of vertices and edges •A subgraph G’ of G is induced by some V’ V and E’ E •Graph properties: Connectivity (node degree, paths) Cyclic vs. acyclic Directed vs. undirected •Graph is sparse if m~n and dense if m~n2 •Graph is complete if m=n2 24 Small‐world network •Every node can be reached from every other by a small number of hops or steps •High clustering coefficient and low mean‐shortest path length (random graphs don’t necessarily have high clustering coefficients •Social networks, the Internet, and biological networks all exhibit small‐ world network characteristics •Six degrees of separation Pilgrim Experiment: Random people from Nebraska were to send a letter (via intermediaries) to a stock broker in Boston.
Load more

Recommended publications
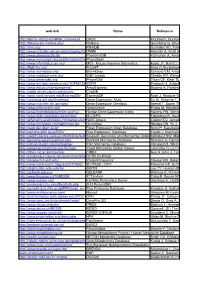
  • Web-Link Name Reference DRSC Flockhart I, Booker M, Kiger A, Et Al.: Flyrnai: the Drosophila Rnai Screening Center Database
    web-link Name Reference http://flyrnai.org/cgi-bin/RNAi_screens.pl DRSC Flockhart I, Booker M, Kiger A, et al.: FlyRNAi: the Drosophila RNAi screening center database. Nucleic Acids Res. 34(Database issue):D489-94 (2006) http://flybase.bio.indiana.edu/ FlyBase Grumbling G, Strelets V.: FlyBase: anatomical data, images and queries. Nucleic Acids Res. 34(Database issue):D484-8 (2006) http://rnai.org/ RNAiDB Gunsalus KC, Yueh WC, MacMenamin P, et al.: RNAiDB and PhenoBlast: web tools for genome-wide phenotypic mapping projects. Nucleic Acids Res. 32(Database issue):D406-10 (2004) http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=OMIMOMIM Hamosh A, Scott AF, Amberger JS, et al.: Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res. 33(Database issue):D514-7 (2005) http://www.phenomicdb.de/ PhenomicDB Kahraman A, Avramov A, Nashev LG, et al.: PhenomicDB: a multi-species genotype/phenotype database for comparative phenomics. Bioinformatics 21(3):418-20 (2005) http://www.worm.mpi-cbg.de/phenobank2/cgi-bin/MenuPage.pyPhenoBank http://www.informatics.jax.org/ MGI - Mouse Genome Informatics Eppig JT, Bult CJ, Kadin JA, et al.: The Mouse Genome Database (MGD): from genes to mice--a community resource for mouse biology. Nucleic Acids Res. 33(Database issue):D471-5 (2005) http://flight.licr.org/ FLIGHT Sims D, Bursteinas B, Gao Q, et al.: FLIGHT: database and tools for the integration and cross-correlation of large-scale RNAi phenotypic datasets. Nucleic Acids Res. 34(Database issue):D479-83 (2006) http://www.wormbase.org/ WormBase Schwarz EM, Antoshechkin I, Bastiani C, et al.: WormBase: better software, richer content.
    [Show full text]
  • Genmapp 2: New Features and Resources for Pathway Analysis Nathan Salomonis Gladstone Institute of Cardiovascular Disease
    Washington University School of Medicine Digital Commons@Becker Open Access Publications 2007 GenMAPP 2: New features and resources for pathway analysis Nathan Salomonis Gladstone Institute of Cardiovascular Disease Kristina Hanspers Gladstone Institute of Cardiovascular Disease Alexander C. Zambon Gladstone Institute of Cardiovascular Disease Karen Vranizan Gladstone Institute of Cardiovascular Disease Steven C. Lawlor Gladstone Institute of Cardiovascular Disease See next page for additional authors Follow this and additional works at: https://digitalcommons.wustl.edu/open_access_pubs Part of the Medicine and Health Sciences Commons Recommended Citation Salomonis, Nathan; Hanspers, Kristina; Zambon, Alexander C.; Vranizan, Karen; Lawlor, Steven C.; Dahlquist, Kam D.; Doniger, Scott .;W Stuart, Josh; Conklin, Bruce R.; and Pico, Alexander R., ,"GenMAPP 2: New features and resources for pathway analysis." BMC Bioinformatics.,. 217. (2007). https://digitalcommons.wustl.edu/open_access_pubs/208 This Open Access Publication is brought to you for free and open access by Digital Commons@Becker. It has been accepted for inclusion in Open Access Publications by an authorized administrator of Digital Commons@Becker. For more information, please contact [email protected]. Authors Nathan Salomonis, Kristina Hanspers, Alexander C. Zambon, Karen Vranizan, Steven C. Lawlor, Kam D. Dahlquist, Scott .W Doniger, Josh Stuart, Bruce R. Conklin, and Alexander R. Pico This open access publication is available at Digital Commons@Becker: https://digitalcommons.wustl.edu/open_access_pubs/208
    [Show full text]
  • Genmapp 2: New Features and Resources for Pathway Analysis Nathan Salomonis Gladstone Institute of Cardiovascular Disease
    Washington University School of Medicine Digital Commons@Becker Open Access Publications 2007 GenMAPP 2: New features and resources for pathway analysis Nathan Salomonis Gladstone Institute of Cardiovascular Disease Kristina Hanspers Gladstone Institute of Cardiovascular Disease Alexander C. Zambon Gladstone Institute of Cardiovascular Disease Karen Vranizan Gladstone Institute of Cardiovascular Disease Steven C. Lawlor Gladstone Institute of Cardiovascular Disease See next page for additional authors Follow this and additional works at: http://digitalcommons.wustl.edu/open_access_pubs Part of the Medicine and Health Sciences Commons Recommended Citation Salomonis, Nathan; Hanspers, Kristina; Zambon, Alexander C.; Vranizan, Karen; Lawlor, Steven C.; Dahlquist, Kam D.; Doniger, Scott .;W Stuart, Josh; Conklin, Bruce R.; and Pico, Alexander R., ,"GenMAPP 2: New features and resources for pathway analysis." BMC Bioinformatics.8,. 217. (2007). http://digitalcommons.wustl.edu/open_access_pubs/208 This Open Access Publication is brought to you for free and open access by Digital Commons@Becker. It has been accepted for inclusion in Open Access Publications by an authorized administrator of Digital Commons@Becker. For more information, please contact [email protected]. Authors Nathan Salomonis, Kristina Hanspers, Alexander C. Zambon, Karen Vranizan, Steven C. Lawlor, Kam D. Dahlquist, Scott .W Doniger, Josh Stuart, Bruce R. Conklin, and Alexander R. Pico This open access publication is available at Digital Commons@Becker: http://digitalcommons.wustl.edu/open_access_pubs/208
    [Show full text]
  • Transcriptomic Uniqueness and Commonality of the Ion Channels and Transporters in the Four Heart Chambers Sanda Iacobas1, Bogdan Amuzescu2 & Dumitru A
    www.nature.com/scientificreports OPEN Transcriptomic uniqueness and commonality of the ion channels and transporters in the four heart chambers Sanda Iacobas1, Bogdan Amuzescu2 & Dumitru A. Iacobas3,4* Myocardium transcriptomes of left and right atria and ventricles from four adult male C57Bl/6j mice were profled with Agilent microarrays to identify the diferences responsible for the distinct functional roles of the four heart chambers. Female mice were not investigated owing to their transcriptome dependence on the estrous cycle phase. Out of the quantifed 16,886 unigenes, 15.76% on the left side and 16.5% on the right side exhibited diferential expression between the atrium and the ventricle, while 5.8% of genes were diferently expressed between the two atria and only 1.2% between the two ventricles. The study revealed also chamber diferences in gene expression control and coordination. We analyzed ion channels and transporters, and genes within the cardiac muscle contraction, oxidative phosphorylation, glycolysis/gluconeogenesis, calcium and adrenergic signaling pathways. Interestingly, while expression of Ank2 oscillates in phase with all 27 quantifed binding partners in the left ventricle, the percentage of in-phase oscillating partners of Ank2 is 15% and 37% in the left and right atria and 74% in the right ventricle. The analysis indicated high interventricular synchrony of the ion channels expressions and the substantially lower synchrony between the two atria and between the atrium and the ventricle from the same side. Starting with crocodilians, the heart pumps the blood through the pulmonary circulation and the systemic cir- culation by the coordinated rhythmic contractions of its upper lef and right atria (LA, RA) and lower lef and right ventricles (LV, RV).
    [Show full text]
  • 1471-2105-8-217.Pdf
    BMC Bioinformatics BioMed Central Software Open Access GenMAPP 2: new features and resources for pathway analysis Nathan Salomonis1,2, Kristina Hanspers1, Alexander C Zambon1, Karen Vranizan1,3, Steven C Lawlor1, Kam D Dahlquist4, Scott W Doniger5, Josh Stuart6, Bruce R Conklin1,2,7,8 and Alexander R Pico*1 Address: 1Gladstone Institute of Cardiovascular Disease, 1650 Owens Street, San Francisco, CA 94158 USA, 2Pharmaceutical Sciences and Pharmacogenomics Graduate Program, University of California, 513 Parnassus Avenue, San Francisco, CA 94143, USA, 3Functional Genomics Laboratory, University of California, Berkeley, CA 94720 USA, 4Department of Biology, Loyola Marymount University, 1 LMU Drive, MS 8220, Los Angeles, CA 90045 USA, 5Computational Biology Graduate Program, Washington University School of Medicine, St. Louis, MO 63108 USA, 6Department of Biomolecular Engineering, University of California, Santa Cruz, CA 95064 USA, 7Department of Medicine, University of California, San Francisco, CA 94143 USA and 8Department of Molecular and Cellular Pharmacology, University of California, San Francisco, CA 94143 USA Email: Nathan Salomonis - [email protected]; Kristina Hanspers - [email protected]; Alexander C Zambon - [email protected]; Karen Vranizan - [email protected]; Steven C Lawlor - [email protected]; Kam D Dahlquist - [email protected]; Scott W Doniger - [email protected]; Josh Stuart - [email protected]; Bruce R Conklin - [email protected]; Alexander R Pico* - [email protected] * Corresponding author Published: 24 June 2007 Received: 16 November 2006 Accepted: 24 June 2007 BMC Bioinformatics 2007, 8:217 doi:10.1186/1471-2105-8-217 This article is available from: http://www.biomedcentral.com/1471-2105/8/217 © 2007 Salomonis et al; licensee BioMed Central Ltd.
    [Show full text]
  • Chromatin Remodelling Complex Dosage Modulates Transcription Factor Function in Heart Development
    ARTICLE Received 5 Aug 2010 | Accepted 11 Jan 2011 | Published 8 Feb 2011 DOI: 10.1038/ncomms1187 Chromatin remodelling complex dosage modulates transcription factor function in heart development Jun K. Takeuchi1,2,*, Xin Lou3,*, Jeffrey M. Alexander1,4, Hiroe Sugizaki2, Paul Delgado-Olguín1, Alisha K. Holloway1, Alessandro D. Mori1, John N. Wylie1, Chantilly Munson5,6, Yonghong Zhu3, Yu-Qing Zhou7, Ru-Fang Yeh8, R. Mark Henkelman7,9, Richard P. Harvey10,11, Daniel Metzger12, Pierre Chambon12, Didier Y. R. Stainier4,5,6, Katherine S. Pollard1,8, Ian C. Scott3,13 & Benoit G. Bruneau1,4,5,14 Dominant mutations in cardiac transcription factor genes cause human inherited congenital heart defects (CHDs); however, their molecular basis is not understood. Interactions between transcription factors and the Brg1/Brm-associated factor (BAF) chromatin remodelling complex suggest potential mechanisms; however, the role of BAF complexes in cardiogenesis is not known. In this study, we show that dosage of Brg1 is critical for mouse and zebrafish cardiogenesis. Disrupting the balance between Brg1 and disease-causing cardiac transcription factors, including Tbx5, Tbx20 and Nkx2–5, causes severe cardiac anomalies, revealing an essential allelic balance between Brg1 and these cardiac transcription factor genes. This suggests that the relative levels of transcription factors and BAF complexes are important for heart development, which is supported by reduced occupancy of Brg1 at cardiac gene promoters in Tbx5 haploinsufficient hearts. Our results reveal complex dosage-sensitive interdependence between transcription factors and BAF complexes, providing a potential mechanism underlying transcription factor haploinsufficiency, with implications for multigenic inheritance of CHDs. 1 Gladstone Institute of Cardiovascular Disease, San Francisco, California 94158, USA.
    [Show full text]
  • Endocrine System Local Gene Expression
    Copyright 2008 By Nathan G. Salomonis ii Acknowledgments Publication Reprints The text in chapter 2 of this dissertation contains a reprint of materials as it appears in: Salomonis N, Hanspers K, Zambon AC, Vranizan K, Lawlor SC, Dahlquist KD, Doniger SW, Stuart J, Conklin BR, Pico AR. GenMAPP 2: new features and resources for pathway analysis. BMC Bioinformatics. 2007 Jun 24;8:218. The co-authors listed in this publication co-wrote the manuscript (AP and KH) and provided critical feedback (see detailed contributions at the end of chapter 2). The text in chapter 3 of this dissertation contains a reprint of materials as it appears in: Salomonis N, Cotte N, Zambon AC, Pollard KS, Vranizan K, Doniger SW, Dolganov G, Conklin BR. Identifying genetic networks underlying myometrial transition to labor. Genome Biol. 2005;6(2):R12. Epub 2005 Jan 28. The co-authors listed in this publication developed the hierarchical clustering method (KP), co-designed the study (NC, AZ, BC), provided statistical guidance (KV), co- contributed to GenMAPP 2.0 (SD) and performed quantitative mRNA analyses (GD). The text of this dissertation contains a reproduction of a figure from: Yeo G, Holste D, Kreiman G, Burge CB. Variation in alternative splicing across human tissues. Genome Biol. 2004;5(10):R74. Epub 2004 Sep 13. The reproduction was taken without permission (chapter 1), figure 1.3. iii Personal Acknowledgments The achievements of this doctoral degree are to a large degree possible due to the contribution, feedback and support of many individuals. To all of you that helped, I am extremely grateful for your support.
    [Show full text]
  • Systematic and Integrative Analysis of Proteomic Data Using Bioinformatics Tools
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 2, No. 5, 2011 Systematic and Integrative Analysis of Proteomic Data using Bioinformatics Tools Rashmi Rameshwari Dr. T. V. Prasad Asst. Professor, Dept. of Biotechnology, Dean (R&D), Lingaya‟s University, Manav Rachna International University, Faridabad, India Faridabad, India Abstract— The analysis and interpretation of relationships or prediction. Expression and interaction experiments tend to between biological molecules is done with the help of networks. be on such a large scale that it is difficult to analyze them, or Networks are used ubiquitously throughout biology to represent indeed grasp the meaning of the results of any analysis. Visual the relationships between genes and gene products. Network representation of such large and scattered quantities of data models have facilitated a shift from the study of evolutionary allows trends that are difficult to pinpoint numerically to stand conservation between individual gene and gene products towards out and provide insight into specific avenues of molecular the study of conservation at the level of pathways and complexes. functions and interactions that may be worth exploring first out Recent work has revealed much about chemical reactions inside of the bunch, either through confirmation or rejection and then hundreds of organisms as well as universal characteristics of later of significance or insignificance to the research problem at metabolic networks, which shed light on the evolution of the hand. With a few recent exceptions, visualization tools were networks. However, characteristics of individual metabolites have been neglected in this network. The current paper provides not designed with the intent of being used for analysis so much an overview of bioinformatics software used in visualization of as to show the workings of a molecular system more clearly.
    [Show full text]
  • Mappfinder: Using Gene Ontology and Genmapp to Create a Global
    Method Open Access MAPPFinder: using Gene Ontology and GenMAPP to create a comment global gene-expression profile from microarray data Scott W Doniger*, Nathan Salomonis*, Kam D Dahlquist*†, Karen Vranizan*‡, Steven C Lawlor* and Bruce R Conklin*†§ Addresses: *Gladstone Institute of Cardiovascular Disease, University of California, San Francisco, CA 94141-9100, USA. †Cardiovascular Research Institute, and §Departments of Medicine and Cellular and Molecular Pharmacology, University of California, San Francisco, ‡ CA 94143, USA. Functional Genomics Lab, University of California, Berkeley, CA 94720, USA. reviews Correspondence: Bruce R Conklin. E-mail: [email protected] Published: 6 January 2003 Received: 11 September 2002 Revised: 8 October 2002 Genome Biology 2003, 4:R7 Accepted: 8 November 2002 The electronic version of this article is the complete one and can be found online at http://genomebiology.com/2003/4/1/R7 reports © 2003 Doniger et al.; licensee BioMed Central Ltd. This is an Open Access article: verbatim copying and redistribution of this article are permitted in all media for any purpose, provided this notice is preserved along with the article's original URL. Abstract deposited research MAPPFinder is a tool that creates a global gene-expression profile across all areas of biology by integrating the annotations of the Gene Ontology (GO) Project with the free software package GenMAPP (http://www.GenMAPP.org). The results are displayed in a searchable browser, allowing the user to rapidly identify GO terms with over-represented numbers of gene- expression changes. Clicking on GO terms generates GenMAPP graphical files where gene relationships can be explored, annotated, and files can be freely exchanged.
    [Show full text]
  • Microarray Data Analysis Tool (Mat)
    MICROARRAY DATA ANALYSIS TOOL (MAT) A Thesis Presented to The Graduate Faculty of The University of Akron In Partial Fulfillment of the Requirements for the Degree Master of Science Sudarshan Selvaraja December, 2008 MICROARRAY DATA ANALYSIS TOOL (MAT) Sudarshan Selvaraja Thesis Approved: Accepted: _______________________ _______________________ Advisor Department Chair Dr. Zhong-Hui Duan Dr. Wolfgang Pelz _______________________ _______________________ Committee Member Dean of the College Dr. Yingcai Xiao Dr. Ronald F. Levant _______________________ _______________________ Committee Member Dean of the Graduate School Dr. Xuan-Hien Dang Dr. George R. Newkome _______________________ Date ii ABSTRACT Microarray is a technology that has been widely used by the biologists to probe the presence of genes in a sample of DNA or RNA. Using the technology, the oligonucleotide probes can be massively parallel immobilized on a microarray chip. It allows the biologists to check the expression levels of thousands of genes together. This thesis develops a software system that includes a database repository to store different microarray datasets and a microarray data analysis tool for analyzing the stored data. The repository currently allows datasets of GenepixPro format to be deposited, although it can be expanded to include datasets of other formats. The user interface of the repository allows users conveniently upload data files and perform preferred data preprocessing and analysis. The analysis methods implemented includes the traditional k-nearest neighbor (kNN) methods and two new kNN methods developed in this study. Additional analysis methods can be added by future developers. The system was tested using a set of microRNA gene expression data. The design and implementation of the software tool are presented in the thesis along with the testing results from the microRNA dataset.
    [Show full text]
  • A Computational Genomics Perspective
    Abstract of thesis entitled Understanding the Pathogenic Fungus Penicillium marne®ei:A Computational Genomics Perspective by James J. Cai for the degree of Doctor of Philosophy at The University of Hong Kong in May 2006 Penicillium marne®ei, a thermally dimorphic fungus that alternates be- tween a ¯lamentous and a yeast growth form in response to changes in its environmental temperature, has become an emerging fungal pathogen endemic in Southeast Asia. De¯ning the genomics of P. marne®ei will provide a better understanding of the fungus. This thesis reports the draft sequence of the P. marne®ei genome as- sembled from 6.6 coverage of the genome through whole genome shotgun sequencing. The 31 Mb genome obtained from the assembly contains 10,060 protein-coding genes. The complete mitochondrial genome is 35 kb long and its gene content and gene order are very similar to that of Aspergillus. An annotation system and P. marne®ei genome database (PMGD) were developed to allow a preliminary annotation of the se- quences and provide an intuitive graphic interface to give curators and users ready access to the annotation and the underlying evidence, and a Matlab-based software package, MBEToolbox, was developed for data analysis in phylogenetics and comparative genomics. A well-designed and structured annotation system and powerful sequence analysis software are essential requirements for the success of large-scale genome analysis projects. Analysis of the gene set of P. marne®ei provided insights into the adaptations required by a fungus to cause disease. The genome encodes a diverse set of putative virulence genes such as proteinase, phospholi- pase, metacaspase and agglutinin, which may enable the fungus to adhere to, colonise and invade the host, adapt to the tissue environment, and avoid the host's humoral and cellular defences of the innate and adaptive immune responses.
    [Show full text]
  • An Exchange Format for Genmapp Biological Pathway Maps
    An Exchange Format for GenMAPP Biological Pathway Maps by Lynn M. Ferrante San Francisco, California August, 2004 A thesis submitted to the faculty of San Francisco State University in partial fulfillment of the requirements for the degree Master of Arts in Biology: Cell and Molecular Copyright by Lynn M. Ferrante 2004 Thesis Committee: Dr. Michael A. Goldman Professor of Biology Dr. Bruce Conklin Associate Professor of Medicine and Cellular and Molecular Pharmacology University of California, San Francisco Dr. Maureen Whalen Professor of Biology Abstract: A biological pathway map is a graphical representation of a known biological pathway. Each source of pathway map data has its own way of storing, analyzing, displaying, and exporting pathway data, and there is no standard for map exchange. Valuable opportunities for data interpretation are lost. The Gene Map Pathway Profiler (GenMAPP) is a freely available software package that helps visualize pathways and genome scale expression data. GenMAPP users must build their own pathway maps or use a small set of provided maps. I investigated a pathway map exchange format for GenMAPP as follows. First, I translated existing metabolic pathway maps to GenMAPP. Next I assessed the proposed BioPAX Pathways Exchange format for exchanging GenMAPP maps. Finally, I devised a pathway exchange format for GenMAPP. ACKNOWLEDGEMENTS This work was carried out at the Gladstone Institute of Cardiovascular Disease at the University of California, San Francisco, under the guidance of Dr. Bruce Conklin. I sincerely thank Dr. Conklin for his support of this work. I am also grateful to the many other members of the lab that assisted me in numerous ways, including Dr.
    [Show full text]