Makin' Math Move
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Why I Hate Microsoft by F.W
Why I hate Microsoft by F.W. van Wensveen Why I hate Microsoft "A personal, lengthy, but highly articulate outburst" by F.W. van Wensveen Table of contents Introduction A brief introduction, or why this paper needed to be written Abstract The management summary 1. From the people who brought you EDLIN Microsoft and innovation 2. The not-so-good, the bad and the ugly The general quality of Microsoft products 3. The power to bind Formats and standards 4. World domination From business to megalomania 5. Bad practice, foul play Exploring the limits of lawful conduct 6. Caveat Emptor Think before you buy 7. Where are you forced to go today? Price gouging and other monopolist practices 8. The road ahead On diminishing returns and continuing trends Appendix A A brief overview of Windows' most serious design flaws Appendix B Links Introduction "One OS to bring them all and in the darkness bind them..." From the title of this paper you may have guessed that I am not very impressed with the guys in Redmond. One might even say that my dislike for Microsoft is a pet hate gone out of control in an almost quixotic fashion. Why is this? Of course I have been accused of personal antipathy, of being jealous of Bill Gates and his billions, and of being prejudiced against all things Microsoft without any reason whatsoever. None of this is true. I have nothing personal against Bill Gates. Why should I? I don't know the man, I've never met him. I agree with those who say he might be the most successful salesman in history. -

Gamification: Sneaking Fitness Game Mechanics Into AAA Games
Andreas Leibetseder Gamification: Sneaking Fitness Game Mechanics into AAA Games Masterarbeit zur Erlangung des akademischen Grades Diplom-Ingenieur Studium Masterstudium Informatik ALPEN-ADRIA UNIVERSITAT¨ KLAGENFURT Fakult¨atf¨urTechnische Wissenschaften (TEWI) Begutachter: Assoc. Prof. Dipl.-Ing. Dr. Mathias Lux Institut f¨urInformationstechnologie (ITEC) March 2016 Eidesstattliche Erkl¨arung{ Affidavit Ich versichere an Eides statt, dass ich die eingereichte wissenschaftliche Arbeit selbstst¨andigverfasst und andere als die angegebenen Hilfsmittel nicht benutzt habe, die w¨ahrenddes Arbeitsvorganges von dritter Seite erfahrene Unterst¨utzung,ein- schließlich signifikanter Betreuungshinweise, vollst¨andig offengelegt habe, die Inhalte, die ich aus Werken Dritter oder eigenen Werken wortw¨ortlich oder sinngem¨aߨubernommen habe, in geeigneter Form gekennzeichnet und den Ur- sprung der Information durch m¨oglichst exakte Quellenangaben (z.B. in Fußnoten) ersichtlich gemacht habe, die Arbeit bisher weder im Inland noch im Ausland einer Pr¨ufungsbeh¨ordevorgelegt habe und zur Plagiatskontrolle eine digitale Version der Arbeit eingereicht habe, die mit der gedruckten Version ¨ubereinstimmt. Ich bin mir bewusst, dass eine tatsachenwidrige Erkl¨arungrechtliche Folgen haben wird. I hereby declare in lieu of an oath that the submitted academic paper is entirely my own work and that no auxiliary materials have been used other than those indicated, I have fully disclosed all assistance received from third parties during the process of writing the paper, including any significant advice from supervisors, any contents taken from the works of third parties or my own works that have been included either literally or in spirit have been appropriately marked and the respective source of the information has been clearly identified with precise bibliographical references (e.g. -

0X0a I Don't Know Gregor Weichbrodt FROHMANN
0x0a I Don’t Know Gregor Weichbrodt FROHMANN I Don’t Know Gregor Weichbrodt 0x0a Contents I Don’t Know .................................................................4 About This Book .......................................................353 Imprint ........................................................................354 I Don’t Know I’m not well-versed in Literature. Sensibility – what is that? What in God’s name is An Afterword? I haven’t the faintest idea. And concerning Book design, I am fully ignorant. What is ‘A Slipcase’ supposed to mean again, and what the heck is Boriswood? The Canons of page construction – I don’t know what that is. I haven’t got a clue. How am I supposed to make sense of Traditional Chinese bookbinding, and what the hell is an Initial? Containers are a mystery to me. And what about A Post box, and what on earth is The Hollow Nickel Case? An Ammunition box – dunno. Couldn’t tell you. I’m not well-versed in Postal systems. And I don’t know what Bulk mail is or what is supposed to be special about A Catcher pouch. I don’t know what people mean by ‘Bags’. What’s the deal with The Arhuaca mochila, and what is the mystery about A Bin bag? Am I supposed to be familiar with A Carpet bag? How should I know? Cradleboard? Come again? Never heard of it. I have no idea. A Changing bag – never heard of it. I’ve never heard of Carriages. A Dogcart – what does that mean? A Ralli car? Doesn’t ring a bell. I have absolutely no idea. And what the hell is Tandem, and what is the deal with the Mail coach? 4 I don’t know the first thing about Postal system of the United Kingdom. -

AARP Work for Yourself@50+
With the generous support of The information provided here is for informational purposes only and should not be considered an individualized recommendation or personalized investment advice. Copyright © 2016 by AARP Foundation All rights reserved. No part of this publication may be reproduced or transmitted in any form by any means, electronic or mechanical, including photocopying, recording, or by any information storage or retrieval system, without written permission from the publisher. ACKNOWLEDGMENTS This program would not have been possible without the support of The Hartford. AARP Foundation would like to recognize its members of the program team that brought this project to life: Emily Allen, Jill Friend, Stacey McDaniel, Marc McDonald, Stephanie Okpala, Donna V.S. Ortega, Aiyshen Padilla, Michael Petrick, Jocelyn Silsby and Lori Strauss. We also would like to recognize the many dedicated individuals and organizations whose efforts and expertise are crucial to the success of our program: AARP Connie Evans and the Association for Enterprise Opportunity (AEO) National Association for Community College Entrepreneurship (NACCE) National Association for Latino Community Asset Builders (NALCAB) Karen Murrell and Higher Heights Consulting 1 Table of Contents Introduction . 4 How to Use the Work for Yourself@50+ Materials . 5 We’re Here to Help.................................................................. 6 Step 1: Explore Your Options . 8 What Does “Working for Yourself” Mean? . 8 The Advantages and Challenges of Self‑Employment .............................. 9 WORKSHEET: Self‑Employment Checklist . 9 WORKSHEET: Do You Have the Disposition to Be Self‑Employed? . 10 Forms of Self‑Employment......................................................... 11 WORKSHEET: The Importance of Goals .............................................13 Talking About Money — How Much Do You Need to Make? .......................14 WORKSHEET: Your Self‑Employment Considerations . -

Bill Gates, "Keynote Address to the Creating Digital Dividends Conference" (18 October 2000)
Voices of Democracy 2 (2007): 227‐243 French 227 BILL GATES, "KEYNOTE ADDRESS TO THE CREATING DIGITAL DIVIDENDS CONFERENCE" (18 OCTOBER 2000) Sandra L. French Radford University Abstract: In the first twenty‐five years of Microsoft, Bill Gates established himself and his company as a powerful social force in the advancement of technology. Gates' keynote address to the 2000 Creating Digital Dividends conference, however, surprised attendees and the press by arguing against the establishment of technology in underdeveloped nations in favor of promotion world equity in healthcare. This speech presents a major shift in Gates' persona, and was largely derided as insincere philanthropy. Key Words: digital divide, technology, Bill Gates, health, crisis, computers. The influence of Bill Gates on technology, society, and global economics is undisputed. He co‐founded Microsoft in 1975 with the vision of a "computer on every desk and in every home"—a computer that would, of course, be running Microsoft software. In the first twenty‐five years of Microsoft, their software products have become the primary method for working, obtaining information, and communicating online. Gates' tenure as Microsoft's chief executive has come to symbolize for many the dawn of the information age and the resultant digital capitalism. Images of Gates are filtered to the public through the mass media and the increasing technological literacy of the global world. Technology is a popular subject of study for contemporary rhetoricians, and has been examined at the micro and macro levels. While much has been written about the development of the personal computer and its impact on society, little attention has been given to technology's business leaders. -

Join PEAK. Join More Than 365 Grantmaking Organizations – Your Peers Leading the Way in Philanthropy – As a Dues-Paying PEAK Grantmaking Organization Member
Where Opportunity Takes Root We are a family-led foundation that creates access to opportunity for people and communities by improving K-12 education, protecting the environment and advancing the quality of life in our home region. waltonfamilyfdn waltonfamilyfoundation waltonfamilyfoundation.org waltonfamilyfdn Welcome to PEAK2020: Courage in Practice PEAK Grantmaking's 16th annual conference and the sector’s largest gathering of grants management professionals. This year is a new milestone – our largest conference organizational culture, and complex grantmaking yet – bringing together more than 900 practitioners, systems to enact this change. along with experts and partners, and supportive businesses. For us, it is an affirmation of the value of We dedicate PEAK2020 to you: Fuel your inspiration what we’ve all built together: a deeply committed, and let’s take the next step together to embrace intensively supportive, member-centered community courage in practice. that’s dedicated to the “how” of grantmaking. Onward! For more than two decades, PEAK Grantmaking The PEAK Grantmaking team & has elevated the profession of grants management your PEAK2020 Conference Co-chairs by focusing on practices and their improvement. Thanks to the participation of 4,500 members across 14 chapters, a group of 200-plus volunteers, and the 365 grantmaking organizations and consultants that Shonda Barnett help power the work as dues-paying members, our Senior Manager – Grants network continues to grow and thrive. Texas Women’s Foundation With the 2019 launch of our Principles for Peak Grantmaking, PEAK issued a call to action to Candy M. Champion philanthropy to courageously lead the way in Grants Manager implementing equitable, effective, and efficient Turner Foundation grantmaking practices – transforming how grants get made. -
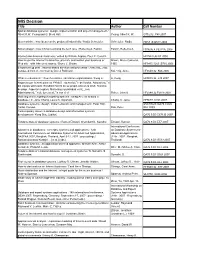
MIS Decision Title Author Call Number Spatial Database Systems : Design, Implementation and Project Management / Albert K.W
MIS Decision Title Author Call Number Spatial database systems : design, implementation and project management / Albert K.W. Yeung and G. Brent Hall. Yeung, Albert K. W. G70.212 .Y48 2007 Idea machine : how ideas can be produced industrially / Nadja Schnetzler. Schnetzler, Nadja. HD53 .S36513 2005 Silicon dragon : how China is winning the tech race / Rebecca A. Fannin. Fannin, Rebecca A. HD9696.8.C62 F36 2008 Internet and American business / edited by William Aspray, Paul. E. Ceruzzi. HE7583.U6 I57 2008 How to use the Internet to advertise, promote and market your business or Brown, Bruce Cameron, Web site-- with little or no money / Bruce C. Brown. 1965- HF5415.1265 .B765 2006 E-business @ print : Internet-based services and processes / Anne KoLnig ; translated from the German by Derek Robinson. KoLnig, Anne. HF5548.32 .K66 2005 What is e-business? : how the internet transforms organisations / Feng Li. Li, Feng. HF5548.32 .L49 2007 Negocios por Intenet para las PYMES : obtencioLn de fondos. AdquisicioLn del equipo adecuado. Establecimiento de su propio sitio en la Web. Sistema de pago. Aspectos legales. Marketing y publicidad en liLnea. AdministracioLn de la relacioLn con el cl Fisher, John G. HF5548.32 F5818 2007 Modeling and designing accounting systems : using Access to build a database / C. Janie Chang, Laura R. Ingraham. Chang, C. Janie. HF5679 .C453 2007 Database systems : design, implementation, and management / Peter Rob, OVERSIZE QA76.9.D26 Carlos Coronel. Rob, Peter. R62 2009 Contemporary issues in database design and information systems development / Keng Siau, [editor]. QA76.9.D3 C67135 2007 Fundamentals of database systems / Ramez Elmasri, Shamkant B. -

Poster Artist Laurie Anderson Laurie’S Daring, Groundbreaking Creations Span the Worlds of Art, Theater, Technology and Experimental Music
THE NATIONAL FILM PRESERVE LTD., with DELL, presents the Founded in 1974 by James Card, Tom Luddy and Bill & Stella Pence Tom Luddy Directors Gary Meyer Julie Huntsinger Managing Director Slavoj Zizek Guest Director Muffy Deslaurier Director of Support Services Karen Schwartzman Director of Sponsorship Development Elizabeth Temple Associate Director of Development Jim Bedford Director of Operations Brandt Garber Production Manager Susan Allen Events Manager Lynne Domingos Operations Manager Bärbel Hacke Hosts Manager Shannon Mitchell Director of Public Relations Marc McDonald Theatre Operations Manager Lucy Lerner ShowCorps Manager Erica Gioga Housing/Travel Manager Kate Sibley Education Programs Dean Melissa DeMicco Development Coordinator Jessica Holt Executive Assistant to the Directors Russell Allen Technical Direction Jon Busch Chapin Cutler Ross Krantz Chief Technician Annette Insdorf Moderator Pierre Rissient Resident Curators Peter Sellars Paolo Cherchi Usai Godfrey Reggio Poster Artist Laurie Anderson Laurie’s daring, groundbreaking creations span the worlds of art, theater, technology and experimental music. Among her many career highlights: the recordings “O Superman”; the feature film HOME OF THE BRAVE; live performances including the multimedia “Songs and Stories for Moby Dick” (1999) and her current tour with “Homeland”; seven books of art and writing; and exhibits in major museums around the world. She was Telluride’s Guest Director in 1991; was appointed NASA’s first artist-in-residence in 2002; and in 2007 received the Dorothy and Lillian Gish Prize for outstanding contributions to the arts. 1 Shows The National Film Preserve, Ltd. A Colorado 501(c)3 non-profit, tax-exempt educational corporation 1a S/Fri 7:00 PM - P/Sat 8:30 AM 1b L/Sat 9:30 PM Directors Emeriti 1 A Tribute to David Fincher Bill & Stella Pence Board of Governors Ken Burns, Peggy Curran, Tom Luddy, Gary Meyer, Milos Stehlik, Marian L. -
39Th TFF Program Guide V10.Pdf
THIS FESTIVAL IS DEDICATED TO Bingham Ray 1954–2012 ©Michael Rauner, courtesy©Michael Rauner, of San Francisco Film Society Jan Sharp 1946–2012 ©Alice Lodge Julie Huntsinger | Directors Tom Luddy Gary Meyer Geoff Dyer | Guest Director Muffy Deslaurier | Director of Support Services Brandt Garber | Production Manager Karen Schwartzman | SVP, External Affairs Elizabeth Temple | VP, Filmanthropy Melissa DeMicco | Development Manager Kirsten Laursen | Executive Assistant to the Directors Kate Sibley | Education Programs Dean Jenny Jacobi | Operations Manager Joanna Lyons | Events Manager Bärbel Hacke | Hosts Manager Shannon Mitchell | Public Relations Manager Marc McDonald | Theater Operations Manager Lucy Lerner | ShowCorps Manager Erica Gioga | Housing/Travel Manager Technical Direction Chapin Cutler | Operations Russell Allen | Sound, Digital Cinema Ross Krantz | Chief Technician Barbara Grassia | Projection Annette Insdorf | Moderator Pierre Rissient | Resident Curators Peter Sellars Paolo Cherchi Usai Publications Editor Jason Silverman (JS) Chief Writer Larry Gross Prized Program Contributors Meredith Brody (MB), Paolo Cherchi Usai (PCU), Mark Danner (MD), Jesse Dubus (JD), Scott Foundas (SF), Barry Jenkins (BJ), Leonard Maltin (LM), Gary Meyer (GM), Kim Morgan (KM), Nicholas O’Neill (NO), Alexander Payne (AP), David Thomson (DT) Tribute Curator Short Films Curator Chris Robinson Barry Jenkins 1 The National Film Preserve, Ltd. A Colorado 501(c)(3) nonprofit, tax-exempt educational corporation Guest Director Founded in 1974 by James Card, Tom Luddy and Bill & Stella Pence Each year, Telluride’s Guest Director serves as a key collaborator in the Directors Emeriti Festival’s programming decisions, bringing new ideas and overlooked films. Bill & Stella Pence Past Guest Directors include Salman Rushdie, Buck Henry, Laurie Anderson, Stephen Sondheim, Peter Sellars, Slavoj Zizek, Alexander Payne, Michael Board of Governors Ondaatje and Caetano Veloso. -
Universidad Nacional De San Agustín Escuela De Postgrado Unidad De
UNIVERSIDAD NACIONAL DE SAN AGUST´IN ESCUELA DE POSTGRADO UNIDAD DE POSTGRADO DE LA FACULTAD DE INGENIERIA DE PRODUCCION Y SERVICIOS IMPLEMENTACION´ DEL LABORATORIO VIRTUAL INMERSIVO APLICADO A LA ENSENANZA~ DE F´ISICA USANDO TECNICAS´ DE GAMIFICATION Tesis presentada por el Bachiller: DIEGO ALONSO IQUIRA BECERRA Para optar por el Grado Acad´emicode: Maestro en Ciencias Inform´atica Con menci´onen Tecnolog´ıasde Informaci´on Asesor: Dr. JOSE´ ALFREDO HERRERA QUISPE AREQUIPA - PERU´ 2018 \En mi tarjeta de visita, soy un presidente de empresa. En mi mente soy un programador de juegos. Pero en mi coraz´onsoy un jugador." Satoru Iwata Resumen Se present´oun laboratorio virtual inmersivo enfocado en el aprendizaje de temas de f´ısicausando gamification, en esta tesis se propuso una metodolog´ıapara la evaluaci´onde software educativo que usen realidad virtual, donde se ha evaluado el software educativo desde tres enfoques: usabilidad pedag´ogica, entorno de realidad virtual y usabilidad en la realidad virtual. Esta propuesta fue implementada y evaluada por profesores y estudiantes. Los resultados experimentales muestran que la usabilidad pedag´ogicaha recibido una aprobaci´ondel 94 % y solo un 2 % de desaprobaci´on,en la evaluaci´ondel entorno virtual se obtuvo una aprobaci´ondel 71 % y una desaprobaci´ondel 6 %, en la evaluaci´onde la usabilidad del entorno virtual se obtuvo una aprobaci´ondel 62 % y solo una desaprobaci´ondel 9 %, estos resultados fueron obtenido mediante encuestas. En la evaluaci´ondel software educativo los alumnos tuvieron que realizar un mismo ejercicio cinco veces. Luego de analizar los datos se encontr´oun aumento de las respuestas correctas del 14 % y una reducci´ondel 60 % del tiempo por ejercicio, una reducci´ondel 30 % de la cantidad de objetos vistos y una reducci´on50 % de respuestas equivocadas en comparaci´onal primer ejercicio realizado, estos resultados demuestran una mejor´ıa en el uso del laboratorio virtual en comparaci´ona la primera prueba. -
Five Year Capital Improvement Plan 2019-2024
Five Year Capital Improvement Plan 2019-2024 Regional Parks General Government Transportation and Public Works Sonoma Water County of Sonoma and Sonoma Water Capital Improvement Plan Authors and Agencies General Services Department Regional Parks Department Caroline Judy, Director Bert Whitaker, Director Transportation and Sonoma Water Public Works Department Grant Davis, General Manager Johannes J. Hoevertsz, Director Development Team Facilities Planning Toni Holland, Capital Project Manager Committee Members Sandra Gallant, Project Manager Caroline Judy, General Services Director Jared Osborn, Data Systems Analyst Keith Lew, Deputy Director Gloria Clark, Publication Designer Bruce Oveson, Sr. Capital Projects Manager Toni Holland, Capital Project Manager Marc McDonald, Real Estate Manager Katherine DiPasqua, Administrative Analyst III, CAO Jane Elias, Energy and Sustainability Manager Tamra Pinoris, ASO II Eric Herrman, Facilities & Maintenance Manager Department and Agency Liaisons Toni Holland, General Services Monique Chapman, Transportation and Public Works Steve Ehret, Regional Parks Elizabeth Tyree, Regional Parks Kent Gylfe, Sonoma Water 2019-2024 Capital Improvement Plan Page B-1 Table of Contents I. EXECUTIVE SUMMARY . B-3 II. GENERAL GOVERNMENT . B-11 Overview . .B-13 Prioritized Project Description List . B-21 Project Funding Sources . .B-25 Projects Organized by Categories . .B-33 Project Details Organized by Priority . .B-38 III. REGIONAL PARKS . C-1 Overview . C-3 Overview of Funding Sources. C-5 Project Details Organized Alphabetically . C-9 List of Regional Parks & Map . C-118 IV. TRANSPORTATION & PUBLIC WORKS . D-1 Overview . D-3 Airport Division . D-3 Integrated Waste Division . D-4 Roads Division . D-4 Transit Division . D-6 Project Details Organized by Division . D-7 V. -

Bill Gates- Biography.Pdf
William H. Gates Chairman Microsoft Corporation William (Bill) H. Gates is chairman of Microsoft Corporation, the worldwide leader in software, services and solutions that help people and businesses realize their full potential. Microsoft had revenues of US$39.79 billion for the fiscal year ending June 2005, and employs more than 61,000 people in 102 countries and regions. On June 15, 2006, Microsoft announced that effective July 2008 Gates will transition out of a day-to-day role in the company to spend more time on his global health and education work at the Bill & Melinda Gates Foundation. After July 2008 Gates will continue to serve as Microsoft’s chairman and an advisor on key development projects. The two-year transition process is to ensure that there is a smooth and orderly transfer of Gates’ daily responsibilities. Effective June 2006, Ray Ozzie has assumed Gates’ previous title as chief software architect and is working side by side with Gates on all technical architecture and product oversight responsibilities at Microsoft. Craig Mundie has assumed the new title of chief research and strategy officer at Microsoft and is working closely with Gates to assume his responsibility for the company’s research and incubation efforts. Born on Oct. 28, 1955, Gates grew up in Seattle with his two sisters. Their father, William H. Gates II, is a Seattle attorney. Their late mother, Mary Gates, was a schoolteacher, University of Washington regent, and chairwoman of United Way International. Gates attended public elementary school and the private Lakeside School. There, he discovered his interest in software and began programming computers at age 13.