DOCSLIB.ORG

Introduction to Biostatistics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction to Biostatistics Introduction to Biostatistics Larry Winner Department of Statistics University of Florida July 8, 2004 2 Contents 1 Introduction 7 1.1 Populations and Samples . 7 1.2 Types of Variables . 8 1.2.1 Quantitative vs Qualitative Variables . 8 1.2.2 Dependent vs Independent Variables . 10 1.3 Parameters and Statistics . 10 1.4 Graphical Techniques . 12 1.5 Basic Probability . 17 1.5.1 Diagnostic Tests . 21 1.6 Basic Study Designs . 23 1.6.1 Observational Studies . 23 1.6.2 Experimental Studies . 25 1.6.3 Other Study Designs . 27 1.7 Reliability and Validity . 29 1.8 Exercises . 31 2 Random Variables and Probability Distributions 35 2.1 The Normal Distribution . 35 2.1.1 Statistical Models . 39 2.2 Sampling Distributions and the Central Limit Theorem . 39 2.2.1 Distribution of Y .................................. 40 2.3 Exercises . 40 3 Statistical Inference – Hypothesis Testing 45 3.1 Introduction to Hypothesis Testing . 45 3.1.1 Large–Sample Tests Concerning µ1 − µ2 (Parallel Groups) . 47 3.2 Elements of Hypothesis Tests . 48 3.2.1 Significance Level of a Test (Size of a Test) . 48 3.2.2 Power of a Test . 49 3.3 Sample Size Calculations to Obtain a Test With Fixed Power . 51 3.4 Small–Sample Tests . 52 3.4.1 Parallel Groups Designs . 52 3.4.2 Crossover Designs . 56 3 4 CONTENTS 3.5 Exercises . 59 4 Statistical Inference – Interval Estimation 65 4.1 Large–Sample Confidence Intervals . 66 4.2 Small–Sample Confidence Intervals . 67 4.2.1 Parallel Groups Designs . 67 4.2.2 Crossover Designs . 68 4.3 Exercises . 69 5 Categorical Data Analysis 71 5.1 2 × 2 Tables . 72 5.1.1 Relative Risk . 72 5.1.2 Odds Ratio . 74 5.1.3 Extension to r × 2 Tables . 76 5.1.4 Difference Between 2 Proportions (Absolute Risk) . 76 5.1.5 Small–Sample Inference — Fisher’s Exact Test . 78 5.1.6 McNemar’s Test for Crossover Designs . 79 5.1.7 Mantel–Haenszel Estimate for Stratified Samples . 81 5.2 Nominal Explanatory and Response Variables . 83 5.3 Ordinal Explanatory and Response Variables . 85 5.4 Nominal Explanatory and Ordinal Response Variable . 87 5.5 Assessing Agreement Among Raters . 89 5.6 Exercises . 91 6 Experimental Design and the Analysis of Variance 97 6.1 Completely Randomized Design (CRD) For Parallel Groups Studies . 97 6.1.1 Test Based on Normally Distributed Data . 98 6.1.2 Test Based on Non–Normal Data . 103 6.2 Randomized Block Design (RBD) For Crossover Studies . 104 6.2.1 Test Based on Normally Distributed Data . 104 6.2.2 Friedman’s Test for the Randomized Block Design . 108 6.3 Other Frequently Encountered Experimental Designs . 109 6.3.1 Factorial Designs . 109 6.3.2 Crossover Designs With Sequence and Period Effects . 114 6.3.3 Repeated Measures Designs . 116 6.4 Exercises . 119 7 Linear Regression and Correlation 129 7.1 Least Squares Estimation of β0 and β1 . 130 7.1.1 Inferences Concerning β1 .............................134 7.2 Correlation Coefficient . 136 7.3 The Analysis of Variance Approach to Regression . 137 7.4 Multiple Regression . 139 CONTENTS 5 7.4.1 Testing for Association Between the Response and the Set of Explanatory Variables . 140 7.4.2 Testing for Association Between the Response and an Individual Explanatory Variable . 140 7.5 Exercises . 144 8 Logistic and Nonlinear Regression 151 8.1 Logistic Regression . 151 8.2 Nonlinear Regression . 156 8.3 Exercises . 158 9 Survival Analysis 163 9.1 Estimating a Survival Function — Kaplan–Meier Estimates . 163 9.2 Log–Rank Test to Compare 2 Population Survival Functions . 166 9.3 Relative Risk Regression (Proportional Hazards Model) . 168 9.4 Exercises . 171 10 Special Topics in Pharmaceutics 179 10.1 Assessment of Pharmaceutical Bioequivalence . 179 10.2 Dose–Response Studies . 181 10.3 Exercises . 183 A Statistical Tables 187 B Bibliography 193 6 CONTENTS Chapter 1 Introduction These notes are intended to provide the student with a conceptual overview of statistical methods with emphasis on applications commonly used in pharmaceutical and epidemiological research. We will briefly cover the topics of probability and descriptive statistics, followed by detailed descriptions of widely used inferential procedures. The goal is to provide the student with the information needed to be able to interpret the types of studies that are reported in academic journals, as well as the ability to perform such analyses. Examples are taken from journals in the pharmaceutical and health sciences fields. 1.1 Populations and Samples A population is the set of all measurements of interest to a researcher. Typically, the population is not observed, but we wish to make statements or inferences concerning it. Populations can be thought of as existing or conceptual. Existing populations are well–defined sets of data containing elements that could be identified explicitly. Examples include: PO1 CD4 counts of every American diagnosed with AIDS as of January 1, 1996. PO2 Amount of active drug in all 20–mg Prozac capsules manufactured in June 1996. PO3 Presence or absence of prior myocardial infarction in all American males between 45 and 64 years of age. Conceptual populations are non–existing, yet visualized, or imaginable, sets of measurements. This could be thought of characteristics of all people with a disease, now or in the near future, for instance. It could also be thought of as the outcomes if some treatment were given to a large group of subjects. In this last setting, we do not give the treatment to all subjects, but we are interested in the outcomes if it had been given to all of them. Examples include: PO4 Bioavailabilities of a drug’s oral dose (relative to i. v. dose) in all healthy subjects under identical conditions. PO5 Presence or absence of myocardial infarction in all current and future high blood pressure patients who receive short–acting calcium channel blockers. 7 8 CHAPTER 1. INTRODUCTION PO6 Positive or negative result of all pregnant women who would ever use a particular brand of home pregnancy test. Samples are observed sets of measurements that are subsets of a corresponding population. Samples are used to describe and make inferences concerning the populations from which they arise. Statistical methods are based on these samples having been taken at random from the population. However, in practice, this is rarely the case. We will always assume that the sample is representative of the population of interest. Examples include: SA1 CD4 counts of 100 AIDS patients on January 1, 1996. SA2 Amount of active drug in 2000 20–mg Prozac capsules manufactured during June 1996. SA3 Prior myocardial infarction status (yes or no) among 150 males aged 45 to 64 years. SA4 Bioavailabilities of an oral dose (relative to i.v. dose) in 24 healthy volunteers. SA5 Presence or absence of myocardial infarction in a fixed period of time for 310 hypertension patients receiving calcium channel blockers. SA6 Test results (positive or negative) among 50 pregnant women taking a home pregnancy test. 1.2 Types of Variables 1.2.1 Quantitative vs Qualitative Variables The measurements to be made are referred to as variables. This refers to the fact that we acknowledge that the outcomes (often referred to as endpoints in the medical world) will vary among elements of the population. Variables can be classified as quantitative (numeric) or qualitative (categorical). We will use the terms numeric and categorical throughout this text, since quantitative and qualitative are so similar. The types of analyses used will depend on what type of variable is being studied. Examples include: VA1 CD4 count represents numbers (or counts) of CD4 lymphocytes per liter of peripheral blood, and thus is numeric. VA2 The amount of active drug in a 20–mg Prozac capsule is the actual number of mg of drug in the capsule, which is numeric. Note, due to random variation in the production process, this number will vary and never be exactly 20.0–mg. VA3 Prior myocardial infarction status can be classified in several ways. If it is classified as either yes or no, it is categorical. If it is classified as number of prior MI’s, it is numeric. Further, numeric variables can be broken into two types: continuous and discrete. Continuous variables are values that can fall anywhere corresponding to points on a line segment. Some examples are weight and diastolic blood pressure. Discrete variables are variables that can take on only a finite (or countably infinite) number of outcomes. Number of previous myocardial infarctions 1.2. TYPES OF VARIABLES 9 and parity are examples of discrete variables. It should be noted that many continuous variables are reported as if they were discrete, and many discrete variables are analyzed as if they were continuous. Similarly, categorical variables also are commonly described in one of two ways: nominal and ordinal. Nominal variables have distinct levels that have no inherent ordering. Hair color and sex are examples of variables that would be described as nominal. On the other hand, ordinal variables have levels that do follow a distinct ordering. Examples in the medical field typically relate to degrees of change in patients after some treatment (such as: vast improvement, moderate improvement, no change, moderate degradation, vast degradation/death). Example 1.1 In studies measuring pain or pain relief, visual analogue scales are often used. These scales involve a continuous line segment, with endpoints labeled as no pain (or no pain relief) and severe (or complete.
Load more

Recommended publications
  • BIOGRAPHICAL SKETCH Garrett M. Fitzmaurice Associate Professor Of
    Principal Investigator/Program Director (Last, First, Middle): BIOGRAPHICAL SKETCH Provide the following information for the key personnel and other significant contributors in the order listed on Form Page 2. Follow this format for each person. DO NOT EXCEED FOUR PAGES. NAME POSITION TITLE Garrett M. Fitzmaurice Associate Professor of Biostatistics eRA COMMONS USER NAME EDUCATION/TRAINING (Begin with baccalaureate or other initial professional education, such as nursing, and include postdoctoral training.) DEGREE INSTITUTION AND LOCATION YEAR(s) FIELD OF STUDY (if applicable) National University of Ireland BA, MA 1983, 1987 Psychology University of London MSc 1986 Quantitative Methods Harvard University ScD 1993 Biostatistics Professional Experience: 1986-1989 Statistician, Department of Psychology, New York University 1989-1990 Teaching Assistant, Department of Biostatistics, Harvard School of Public Health 1990-1993 Teaching Fellow in Biostatistics, Department of Biostatistics, Harvard SPH 1993-1994 Post-doctoral Research Fellow, Department of Biostatistics, Harvard SPH 1994-1997 Research Fellow, Nuffield College, Oxford University, United Kingdom 1997-1999 Assistant Professor of Biostatistics, Harvard School of Public Health 1999-present Associate Professor of Biostatistics, Harvard School of Public Health 2004-present Associate Professor of Medicine (Biostatistics), Harvard Medical School 2004-present Biostatistician, Division of General Medicine, Brigham and Women’s Hospital, Boston 2006-present Foreign Adjunct Professor of Biostatistics,
    [Show full text]
  • TUTORIAL in BIOSTATISTICS: the Self-Controlled Case Series Method
    STATISTICS IN MEDICINE Statist. Med. 2005; 0:1–31 Prepared using simauth.cls [Version: 2002/09/18 v1.11] TUTORIAL IN BIOSTATISTICS: The self-controlled case series method Heather J. Whitaker1, C. Paddy Farrington1, Bart Spiessens2 and Patrick Musonda1 1 Department of Statistics, The Open University, Milton Keynes, MK7 6AA, UK. 2 GlaxoSmithKline Biologicals, Rue de l’Institut 89, B-1330 Rixensart, Belgium. SUMMARY The self-controlled case series method was developed to investigate associations between acute outcomes and transient exposures, using only data on cases, that is, on individuals who have experienced the outcome of interest. Inference is within individuals, and hence fixed covariates effects are implicitly controlled for within a proportional incidence framework. We describe the origins, assumptions, limitations, and uses of the method. The rationale for the model and the derivation of the likelihood are explained in detail using a worked example on vaccine safety. Code for fitting the model in the statistical package STATA is described. Two further vaccine safety data sets are used to illustrate a range of modelling issues and extensions of the basic model. Some brief pointers on the design of case series studies are provided. The data sets, STATA code, and further implementation details in SAS, GENSTAT and GLIM are available from an associated website. key words: case series; conditional likelihood; control; epidemiology; modelling; proportional incidence Copyright c 2005 John Wiley & Sons, Ltd. 1. Introduction The self-controlled case series method, or case series method for short, provides an alternative to more established cohort or case-control methods for investigating the association between a time-varying exposure and an outcome event.
    [Show full text]
  • Receiver Operating Characteristic (ROC) Curve: Practical Review for Radiologists
    Receiver Operating Characteristic (ROC) Curve: Practical Review for Radiologists Seong Ho Park, MD1 The receiver operating characteristic (ROC) curve, which is defined as a plot of Jin Mo Goo, MD1 test sensitivity as the y coordinate versus its 1-specificity or false positive rate Chan-Hee Jo, PhD2 (FPR) as the x coordinate, is an effective method of evaluating the performance of diagnostic tests. The purpose of this article is to provide a nonmathematical introduction to ROC analysis. Important concepts involved in the correct use and interpretation of this analysis, such as smooth and empirical ROC curves, para- metric and nonparametric methods, the area under the ROC curve and its 95% confidence interval, the sensitivity at a particular FPR, and the use of a partial area under the ROC curve are discussed. Various considerations concerning the collection of data in radiological ROC studies are briefly discussed. An introduc- tion to the software frequently used for performing ROC analyses is also present- ed. he receiver operating characteristic (ROC) curve, which is defined as a Index terms: plot of test sensitivity as the y coordinate versus its 1-specificity or false Diagnostic radiology positive rate (FPR) as the x coordinate, is an effective method of evaluat- Receiver operating characteristic T (ROC) curve ing the quality or performance of diagnostic tests, and is widely used in radiology to Software reviews evaluate the performance of many radiological tests. Although one does not necessar- Statistical analysis ily need to understand the complicated mathematical equations and theories of ROC analysis, understanding the key concepts of ROC analysis is a prerequisite for the correct use and interpretation of the results that it provides.
    [Show full text]
  • Biometrics & Biostatistics
    Hanley and Moodie, J Biomet Biostat 2011, 2:5 Biometrics & Biostatistics http://dx.doi.org/10.4172/2155-6180.1000124 Research Article Article OpenOpen Access Access Sample Size, Precision and Power Calculations: A Unified Approach James A Hanley* and Erica EM Moodie Department of Epidemiology, Biostatistics, and Occupational Health, McGill University, Canada Abstract The sample size formulae given in elementary biostatistics textbooks deal only with simple situations: estimation of one, or a comparison of at most two, mean(s) or proportion(s). While many specialized textbooks give sample formulae/tables for analyses involving odds and rate ratios, few deal explicitly with statistical considera tions for slopes (regression coefficients), for analyses involving confounding variables or with the fact that most analyses rely on some type of generalized linear model. Thus, the investigator is typically forced to use “black-box” computer programs or tables, or to borrow from tables in the social sciences, where the emphasis is on cor- relation coefficients. The concern in the – usually very separate – modules or stand alone software programs is more with user friendly input and output. The emphasis on numerical exactness is particularly unfortunate, given the rough, prospective, and thus uncertain, nature of the exercise, and that different textbooks and software may give different sample sizes for the same design. In addition, some programs focus on required numbers per group, others on an overall number. We present users with a single universal (though sometimes approximate) formula that explicitly isolates the impacts of the various factors one from another, and gives some insight into the determinants for each factor.
    [Show full text]
  • The American Statistician
    This article was downloaded by: [T&F Internal Users], [Rob Calver] On: 01 September 2015, At: 02:24 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: 5 Howick Place, London, SW1P 1WG The American Statistician Publication details, including instructions for authors and subscription information: http://www.tandfonline.com/loi/utas20 Reviews of Books and Teaching Materials Published online: 27 Aug 2015. Click for updates To cite this article: (2015) Reviews of Books and Teaching Materials, The American Statistician, 69:3, 244-252, DOI: 10.1080/00031305.2015.1068616 To link to this article: http://dx.doi.org/10.1080/00031305.2015.1068616 PLEASE SCROLL DOWN FOR ARTICLE Taylor & Francis makes every effort to ensure the accuracy of all the information (the “Content”) contained in the publications on our platform. However, Taylor & Francis, our agents, and our licensors make no representations or warranties whatsoever as to the accuracy, completeness, or suitability for any purpose of the Content. Any opinions and views expressed in this publication are the opinions and views of the authors, and are not the views of or endorsed by Taylor & Francis. The accuracy of the Content should not be relied upon and should be independently verified with primary sources of information. Taylor and Francis shall not be liable for any losses, actions, claims, proceedings, demands, costs, expenses, damages, and other liabilities whatsoever or howsoever caused arising directly or indirectly in connection with, in relation to or arising out of the use of the Content. This article may be used for research, teaching, and private study purposes.
    [Show full text]
  • Epidemiology and Biostatistics (EPBI) 1
    Epidemiology and Biostatistics (EPBI) 1 Epidemiology and Biostatistics (EPBI) Courses EPBI 2219. Biostatistics and Public Health. 3 Credit Hours. This course is designed to provide students with a solid background in applied biostatistics in the field of public health. Specifically, the course includes an introduction to the application of biostatistics and a discussion of key statistical tests. Appropriate techniques to measure the extent of disease, the development of disease, and comparisons between groups in terms of the extent and development of disease are discussed. Techniques for summarizing data collected in samples are presented along with limited discussion of probability theory. Procedures for estimation and hypothesis testing are presented for means, for proportions, and for comparisons of means and proportions in two or more groups. Multivariable statistical methods are introduced but not covered extensively in this undergraduate course. Public Health majors, minors or students studying in the Public Health concentration must complete this course with a C or better. Level Registration Restrictions: May not be enrolled in one of the following Levels: Graduate. Repeatability: This course may not be repeated for additional credits. EPBI 2301. Public Health without Borders. 3 Credit Hours. Public Health without Borders is a course that will introduce you to the world of disease detectives to solve public health challenges in glocal (i.e., global and local) communities. You will learn about conducting disease investigations to support public health actions relevant to affected populations. You will discover what it takes to become a field epidemiologist through hands-on activities focused on promoting health and preventing disease in diverse populations across the globe.
    [Show full text]
  • Medicine Safety “Pharmacovigilance” Fact Sheet
    MINISTRY OF MEDICAL SERVICES MINISTRY OF PUBLIC HEALTH AND SANITATION PHARMACY AND POISONS BOARD MEDICINE SAFETY “PHARMACOVIGILANCE” FACT SHEET What is medicine safety? Medicine safety, also referred to as Pharmacovigilance refers to the science of collecting, monitoring, researching, assessing and evaluating information from healthcare providers and patients on the adverse effects of medicines, biological products, herbals and traditional medicines. It aims at identifying new information about hazards, and preventing harm to patients. What is an Adverse Drug Reaction? The World Health Organization defines an adverse drug reaction (ADR) as "A response to a drug which is noxious and unintended, and which occurs at doses normally used or tested in man for the prophylaxis, diagnosis, or therapy of disease, or for the modification of physiological function". Simply put, when the doctor prescribes you medicines, he expects the desirable effects of them. The undesired effects of the medicines is the ADR or, commonly known as “side effects”. An adverse drug reaction is considered to be serious when it is suspected of causing death, poses danger to life, results in admission to hospital, prolongs hospitalization, leads to absence from productive activity, increased investigational or treatment costs, or birth defects. Age, gender, previous history of allergy or reaction, race and genetic factors, multiple medicine therapy and presence of concomitant disease processes may predispose one to adverse effects. Why monitor adverse drug reactions? Before registration and marketing of a medicine, its safety and efficacy experience is based primarily on clinical trials. Some important adverse reactions may not be detected early or may even be rare.
    [Show full text]
  • Biostatistics (EHCA 5367)
    The University of Texas at Tyler Executive Health Care Administration MPA Program Spring 2019 COURSE NUMBER EHCA 5367 COURSE TITLE Biostatistics INSTRUCTOR Thomas Ross, PhD INSTRUCTOR INFORMATION email - [email protected] – this one is checked once a week [email protected] – this one is checked Monday thru Friday Phone - 828.262.7479 REQUIRED TEXT: Wayne Daniel and Chad Cross, Biostatistics, 10th ed., Wiley, 2013, ISBN: 978-1- 118-30279-8 COURSE DESCRIPTION This course is designed to teach students the application of statistical methods to the decision-making process in health services administration. Emphasis is placed on understanding the principles in the meaning and use of statistical analyses. Topics discussed include a review of descriptive statistics, the standard normal distribution, sampling distributions, t-tests, ANOVA, simple and multiple regression, and chi-square analysis. Students will use Microsoft Excel or other appropriate computer software in the completion of assignments. COURSE LEARNING OBJECTIVES Upon completion of this course, the student will be able to: 1. Use descriptive statistics and graphs to describe data 2. Understand basic principles of probability, sampling distributions, and binomial, Poisson, and normal distributions 3. Formulate research questions and hypotheses 4. Run and interpret t-tests and analyses of variance (ANOVA) 5. Run and interpret regression analyses 6. Run and interpret chi-square analyses GRADING POLICY Students will be graded on homework, midterm, and final exam, see weights below. ATTENDANCE/MAKE UP POLICY All students are expected to attend all of the on-campus sessions. Students are expected to participate in all online discussions in a substantive manner. If circumstances arise that a student is unable to attend a portion of the on-campus session or any of the online discussions, special arrangements must be made with the instructor in advance for make-up activity.
    [Show full text]
  • Biostatistics
    Biostatistics As one of the nation’s premier centers of biostatistical research, the Department of Biostatistics is dedicated to addressing high priority public health and biomedical issues and driving scientific discovery through specialized analytic techniques and catalyzing interdisciplinary research. Our world-renowned experts are engaged in developing novel statistical methods to break new ground in current research frontiers. The Department has become a leader in mission the analysis and interpretation of complex data in genetics, brain science, clinical trials, and personalized medicine. Our mission is to improve disease prevention, In these and other areas, our faculty play key roles in diagnosis, treatment, and the public’s health by public health, mental health, social science, and biomedical developing new theoretical results and applied research as collaborators and conveners. Current research statistical methods, collaborating with scientists in is wide-ranging. designing informative experiments and analyzing their data to weigh evidence and obtain valid Examples of our work: findings, and educating the next generation of biostatisticians through an innovative and relevant • Researching efficient statistical methods using large-scale curriculum, hands-on experience, and exposure biomarker data for disease risk prediction, informing to the latest in research findings and methods. clinical trial designs, discovery of personalized treatment regimes, and guiding new and more effective interventions history • Analyzing data to
    [Show full text]
  • Biostatistics (BIOSTAT) 1
    Biostatistics (BIOSTAT) 1 This course covers practical aspects of conducting a population- BIOSTATISTICS (BIOSTAT) based research study. Concepts include determining a study budget, setting a timeline, identifying study team members, setting a strategy BIOSTAT 301-0 Introduction to Epidemiology (1 Unit) for recruitment and retention, developing a data collection protocol This course introduces epidemiology and its uses for population health and monitoring data collection to ensure quality control and quality research. Concepts include measures of disease occurrence, common assurance. Students will demonstrate these skills by engaging in a sources and types of data, important study designs, sources of error in quarter-long group project to draft a Manual of Operations for a new epidemiologic studies and epidemiologic methods. "mock" population study. BIOSTAT 302-0 Introduction to Biostatistics (1 Unit) BIOSTAT 429-0 Systematic Review and Meta-Analysis in the Medical This course introduces principles of biostatistics and applications Sciences (1 Unit) of statistical methods in health and medical research. Concepts This course covers statistical methods for meta-analysis. Concepts include descriptive statistics, basic probability, probability distributions, include fixed-effects and random-effects models, measures of estimation, hypothesis testing, correlation and simple linear regression. heterogeneity, prediction intervals, meta regression, power assessment, BIOSTAT 303-0 Probability (1 Unit) subgroup analysis and assessment of publication
    [Show full text]
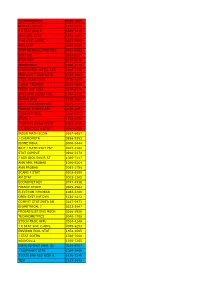
  • Econometrica 0012-9682 Biostatistics 1465-4644 J R
    ECONOMETRICA 0012-9682 BIOSTATISTICS 1465-4644 J R STAT SOC B 1369-7412 ANN APPL STAT 1932-6157 J AM STAT ASSOC 0162-1459 ANN STAT 0090-5364 STAT METHODS MED RES 0962-2802 STAT SCI 0883-4237 STAT MED 0277-6715 BIOMETRICS 0006-341X CHEMOMETR INTELL LAB 0169-7439 IEEE ACM T COMPUT BI 1545-5963 J BUS ECON STAT 0735-0015 J QUAL TECHNOL 0022-4065 FUZZY SET SYST 0165-0114 STAT APPL GENET MOL 1544-6115 PHARM STAT 1539-1604 MULTIVAR BEHAV RES 0027-3171 PROBAB THEORY REL 0178-8051 J COMPUT BIOL 1066-5277 STATA J 1536-867X J COMPUT GRAPH STAT 1061-8600 J R STAT SOC A STAT 0964-1998 INSUR MATH ECON 0167-6687 J CHEMOMETR 0886-9383 BIOMETRIKA 0006-3444 BRIT J MATH STAT PSY 0007-1102 STAT COMPUT 0960-3174 J AGR BIOL ENVIR ST 1085-7117 ANN APPL PROBAB 1050-5164 ANN PROBAB 0091-1798 SCAND J STAT 0303-6898 AM STAT 0003-1305 ECONOMET REV 0747-4938 FINANC STOCH 0949-2984 ELECTRON J PROBAB 1083-6489 OPEN SYST INF DYN 1230-1612 COMPUT STAT DATA AN 0167-9473 BIOMETRICAL J 0323-3847 PROBABILIST ENG MECH 0266-8920 TECHNOMETRICS 0040-1706 STOCH PROC APPL 0304-4149 J R STAT SOC C-APPL 0035-9254 ENVIRON ECOL STAT 1352-8505 J STAT SOFTW 1548-7660 BERNOULLI 1350-7265 INFIN DIMENS ANAL QU 0219-0257 J BIOPHARM STAT 1054-3406 STOCH ENV RES RISK A 1436-3240 TEST 1133-0686 ASTIN BULL 0515-0361 ADV APPL PROBAB 0001-8678 J TIME SER ANAL 0143-9782 MATH POPUL STUD 0889-8480 COMB PROBAB COMPUT 0963-5483 LIFETIME DATA ANAL 1380-7870 METHODOL COMPUT APPL 1387-5841 ECONOMET J 1368-4221 STATISTICS 0233-1888 J APPL PROBAB 0021-9002 J MULTIVARIATE ANAL 0047-259X ENVIRONMETRICS 1180-4009
    [Show full text]
  • Curriculum Vitae Jianwen Cai
    CURRICULUM VITAE JIANWEN CAI Business Address: Department of Biostatistics, CB # 7420 The University of North Carolina at Chapel Hill Chapel Hill, NC 27599-7420 TEL: (919) 966-7788 FAX: (919) 966-3804 Email: [email protected] Education: 1992 - Ph.D. (Biostatistics), University of Washington, Seattle, Washington. 1989 - M.S. (Biostatistics), University of Washington, Seattle, Washington. 1985 - B.S. (Mathematics), Shandong University, Jinan, P. R. China. Positions: Teaching Assistant: Department of Biostatistics, University of Washington, 1988 - 1990. Research Assistant: Cardiovascular Health Study, University of Washington, 1988 - 1990. Fred Hutchinson Cancer Research Center, 1990 - 1992. Research Associate: Fred Hutchinson Cancer Research Center, 1992 - 1992. Assistant Professor: Department of Biostatistics, University of North Carolina at Chapel Hill, 1992 - 1999. Associate Professor: Department of Biostatistics, University of North Carolina at Chapel Hill, 1999 - 2004. Professor: Department of Biostatistics, University of North Carolina at Chapel Hill, 2004 - present. Interim Chair: Department of Biostatistics, University of North Carolina at Chapel Hill, 2006. Associate Chair: Department of Biostatistics, University of North Carolina at Chapel Hill, 2006-present. Professional Societies: American Statistical Association (ASA) International Biometric Society (ENAR) Institute of Mathematical Statistics (IMS) International Chinese Statistical Association (ICSA) 1 Research Interests: Survival Analysis and Regression Models, Design and Analysis of Clinical Trials, Analysis of Correlated Responses, Cancer Biology, Cardiovascular Disease Research, Obesity Research, Epidemiological Models. Awards/Honors: UNC School of Public Health McGavran Award for Excellence in Teaching, 2004. American Statistical Association Fellow, 2005 Institute of Mathematical Statistics Fellow, 2009 Professional Service: Associate Editor: Biometrics: 2000-2010. Lifetime Data Analysis: 2002-. Statistics in Biosciences: 2009-. Board Member: ENAR Regional Advisory Board, 1996-1998.
    [Show full text]