DOCSLIB.ORG

Image Processing on Optimal Volume Sampling Lattices

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Image Processing on Optimal Volume Sampling Lattices Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1314 Image processing on optimal volume sampling lattices Thinking outside the box ELISABETH SCHOLD LINNÉR ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-554-9406-3 UPPSALA urn:nbn:se:uu:diva-265340 2015 Dissertation presented at Uppsala University to be publicly examined in Pol2447, Informationsteknologiskt centrum (ITC), Lägerhyddsvägen 2, hus 2, Uppsala, Friday, 18 December 2015 at 10:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Professor Alexandre Falcão (Institute of Computing, University of Campinas, Brazil). Abstract Schold Linnér, E. 2015. Image processing on optimal volume sampling lattices. Thinking outside the box. (Bildbehandling på optimala samplingsgitter. Att tänka utanför ramen). Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1314. 98 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-554-9406-3. This thesis summarizes a series of studies of how image quality is affected by the choice of sampling pattern in 3D. Our comparison includes the Cartesian cubic (CC) lattice, the body- centered cubic (BCC) lattice, and the face-centered cubic (FCC) lattice. Our studies of the lattice Brillouin zones of lattices of equal density show that, while the CC lattice is suitable for functions with elongated spectra, the FCC lattice offers the least variation in resolution with respect to direction. The BCC lattice, however, offers the highest global cutoff frequency. The difference in behavior between the BCC and FCC lattices is negligible for a natural spectrum. We also present a study of pre-aliasing errors on anisotropic versions of the CC, BCC, and FCC sampling lattices, revealing that the optimal choice of sampling lattice is highly dependent on lattice orientation and anisotropy. We suggest a new reference function for studies of aliasing errors on alternative sampling lattices. This function has a spherical spectrum, and a frequency content proportional to the distance from the origin, facilitating studies of pre-aliasing in spatial domain. The accuracy of anti-aliased Euclidean distance transform is improved by application of more sofisticated methods for computing the sub-spel precision term. We find that both accuracy and precision are higher on the BCC and FCC lattices than on the CC lattice. We compare the performance of several intensity-weighted distance transforms on MRI data, and find that the derived segmentation result, with respect to relative error in segmented volume, depends neither on the sampling lattice, nor on the sampling density. Lastly, we present LatticeLibrary, a open source C++ library for processing of sampled data, supporting a number of common image processing methods for CC, BCC, and FCC lattices. We also introduce BccFccRaycaster, a tool for visualizing data sampled on CC, BCC, and FCC lattices. We believe that the work summarized in this thesis provide both the motivation and the tools for continuing research on application of the BCC and FCC lattices in image processing and analysis. Keywords: BCC, FCC, aliasing, distance transform, segmentation Elisabeth Schold Linnér, Department of Information Technology, Division of Visual Information and Interaction, Box 337, Uppsala University, SE-751 05 Uppsala, Sweden. © Elisabeth Schold Linnér 2015 ISSN 1651-6214 ISBN 978-91-554-9406-3 urn:nbn:se:uu:diva-265340 (http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-265340) Till min stora förvåning. List of papers This thesis is based on the following papers, which are referred to in the text by their Roman numerals. I E. Linnér and R. Strand. Aliasing Properties of Voxels in Three-Dimensional Sampling Lattices. In Large Scale Scientific Computing, Sozopol, Bulgaria, I. Lirkov, S. Margenov, and J. Wasinewski´ (Eds.), Lecture Notes in Computer Science, 7116: pp 507–514, Jun. 2011. c 2012, Springer-Verlag Berlin Heidelberg II E. Linnér and R. Strand. A Graph-Based Implementation of the Anti-Aliased Euclidean Distance Transform. In 22nd International Conference on Pattern Recognition (ICPR), Stockholm, Sweden: pp 1025-1030, Aug. 2014. c 2014 IEEE III E. Linnér and R. Strand. Anti-Aliased Euclidean Distance Transform on 3D Sampling Lattices. In Discrete Geometry for Computer Imagery, E. Barcucci, A. Frosini, and S. Rinaldi (Eds.), Siena, Italy, Lecture Notes in Computer Science, 8668: pp 88-98, Sep. 2014. c 2014, Springer International Publishing Switzerland IV E. Schold Linnér and R. Strand. Pre-aliasing and anisotropy on the CC, BCC, and FCC sampling lattices. Submitted for journal publication. V E. Schold Linnér, J. Kullberg, and R. Strand. Fuzzy Segmentation of Synthetic and MRI Volume Data sampled on Optimal Lattices. Submitted journal for publication. VI E. Schold Linnér, M. Morén, K.-O. Smed, J. Nysjö, and R. Strand. LatticeLibrary and BccFccRaycaster: Software for processing and viewing 3D data on optimal sampling lattices. Submitted for journal publication. Reprints were made with permission from the publishers. All papers were researched and written under the supervision of R. Strand. The frequency domain study in Paper I was performed by R. Strand. In Paper V, planning and implementation were the work of E. Linnér, and data acquisi- tion was the joint work of E. Linnér and J. Kullberg. LatticeLibrary, published in Paper VI is the work of E. Linnér, while BccFccRaycaster is implemented by M. Morén and K.-O. Smed, under the supervision of E. Linnér and J. Nysjö. Related work In addition to the papers included in this thesis, the author has also written or contributed to the following publications: • E. Linnér and R. Strand. Comparison of normalized convolution on square and Hexagonal grids. In Proceedings SSBA’11 Symposium on Image Analysis, Stockholm, Sweden, 2011. • E. Linnér and R. Strand. Comparison of restoration quality on square and hexagonal grids using normalized convolution. In 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan: pp 3046- 3049, Nov. 2012. • R. Strand, F. Malmberg, P. K. Saha, and E. Linnér. The Minimum Barrier Distance - Stability to Seed Point Position. In Discrete Geometry for Computer Imagery, E. Barcucci, A. Frosini, and S. Rinaldi (Eds.), Siena, Italy, Lecture Notes in Computer Science, 8668: pp 111-121, Sep. 2014. Contents 1 Initial remarks ............................................................................................ 17 2 Introduction to computerized image processing and analysis ................ 19 2.1 Image pre-processing ..................................................................... 21 2.1.1 Convolutional filtering .................................................... 21 2.1.2 Filtering in frequency domain ........................................ 21 2.2 Image processing ............................................................................ 23 2.2.1 Image segmentation ......................................................... 23 2.2.2 Distance transformation .................................................. 25 2.2.3 Registration ...................................................................... 28 2.3 Image analysis ................................................................................ 28 3 Sampling theory ......................................................................................... 30 3.1 One-dimensional point-sampling .................................................. 30 3.2 Interpolation and super-sampling .................................................. 33 3.3 Sampling lattices ............................................................................ 35 3.4 Non-band-limited functions .......................................................... 39 3.4.1 Studies in the frequency domain .................................... 40 3.4.2 Studies in the spatial domain .......................................... 45 3.5 Anisotropic sampling ..................................................................... 48 4 Image acquisition on optimal sampling lattices ...................................... 52 4.1 Acquisition of 2D images .............................................................. 52 4.1.1 Photography ..................................................................... 52 4.1.2 Sonography ...................................................................... 53 4.2 Acquisition of volume images ....................................................... 54 4.2.1 Computed tomography .................................................... 54 4.2.2 Emission Tomography ..................................................... 57 4.2.3 Magnetic Resonance Imaging ......................................... 58 4.2.4 3D sonography ................................................................. 60 5 Image processing and analysis on optimal sampling lattices ................. 61 5.1 Raster scanning .............................................................................. 62 5.2 Surface area of fuzzy binary objects ............................................. 63 5.3 Distance transforms and segmentation ......................................... 64 5.3.1 Wave-front propagation ................................................... 65 5.3.2 Improving the anti-aliased Euclidean distance transform .......................................................................... 66 5.3.3 Seeded segmentation on optimal lattices ....................... 69 5.4 Fourier transform ..........................................................................
Load more

Recommended publications
  • Near-Infrared Chemical Imaging and the PAT Initiative NIR-CI Adds a Completely New Dimension to Conventional NIR Spectroscopy
    Molecular Spectroscopy Workbench Near-infrared Chemical Imaging and the PAT Initiative NIR-CI adds a completely new dimension to conventional NIR spectroscopy. E. Neil Lewis, Joe Schoppelrei, and Eunah Lee Dear and gentle readers, this month I present an important other manufacturing steps have on the final dosage form? To tool in the process analytical technologies (PAT) initiative: encourage the PAT initiative FDA is streamlining the mecha- Near-infrared chemical imaging (NIR-CI). You might wonder nism for adopting new technologies in pharmaceutical manu- why I am seemingly concentrating on IR and NIR. The an- facturing. swer is quite simple: I need all the heat I can get, here in New York. Seriously, E. Neil Lewis, Joe Schoppelrei, and The Role of Near-infrared Chemical Imaging (NIR-CI) Eunah Lee of Spectral Dimensions (Olney, MD) have put to- A typical tablet is not just a pressed block of a single material, gether an excellent explanation of what NIR-CI is and what but rather a complex matrix containing one or more active its part in PAT is and will be. For those of you who do not pharmaceutical ingredients (APIs), fillers, binders, disinte- know Neil Lewis, he is one of the pioneers in IR and NIR im- grants, lubricants, and other materials. A basic problem in aging. He has won numerous awards for his research at the pharmaceutical manufacturing is that a relatively simple for- National Institutes of Health (NIH) and subsequent accom- mulation with identical ingredients can produce widely vary- plishments. It is truly exciting to have this paper in my hum- ing therapeutic performance depending upon how the ingre- ble column and I know you will find it informative and enter- dients are distributed in the final matrix.
    [Show full text]
  • Comprehensive Bibliography on Martian Meteorites (Compiled by C
    Comprehensive Bibliography on Martian Meteorites (compiled by C. Meyer, March 2008) Abu Aghreb A.E., Ghadi A.M., Schlüter J., Schultz L. and Thiedig F. (2003) Hamadah al Hamra and Dar al Gani: A comparison of two meteorite fields in the Libyan Sahara (abs). Meteoritics & Planet. Sci. 38, A48. Agee Carl B. (2002) Garnet and majorite fractionation in the early Earth and Mars (abs#1862). Lunar Planet. Sci. XXXIII Lunar Planetary Institute, Houston. (CD-ROM). (see address of LPI in Appendix III) Agee C.B., Bogard Don D., Draper D.S., Jones J.H., Meyer Chuck and Mittlefehldt D.W. (2000) Proposed science requirements and acquisition priorities for the first Mars sample return (abs). In Concept and Approaches for Mars Exploration. Part 1 (ed. S. Hubbard) LPI Contribution # 1062. Lunar Planetary Institute, Houston. Agee C.B. and Draper Dave S. (2003) Melting of model Martian mantle at high pressure: Implications for the composition of the Martian basalt source region (abs#1408). Lunar Planet. Sci. Conf. 34th, Lunar Planetary Institute, Houston (CD-ROM). Agerkvist D.P. and Vistisen L. (1993) Mössbauer spectroscopy of the SNC meteorite Zagami (abs). Lunar Planet. Sci. XXIV, 1-2. Lunar Planetary Institute, Houston. Zagami Agerkvist D.P., Vistisen L., Madsen M.B. and Knudsen J.M. (1994) Magnetic properties of Zagami and Nakhla (abs). Lunar Planet. Sci. XXV, 1-2. Lunar Planetary Institute, Houston. Zagami Nakhla Akai J. (1997) Characteristics of iron-oxide and iron-sulfide grains in meteorites and terrestrial sediments, with special references to magnetite grains in Allan Hills 84001 (abs). Meteoritics & Planet. Sci.
    [Show full text]
  • Army Acquisition Workforce Dependency on E-Mail for Formal
    ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY .ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY ii Table of Contents Table of Contents ............................................................................................................................ ii List of Figures ................................................................................................................................ vi Abstract ......................................................................................................................................... vii Chapter 1—Introduction ................................................................................................................. 1 Background and Motivation .................................................................................................
    [Show full text]
  • Inviwo — a Visualization System with Usage Abstraction Levels
    IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL X, NO. Y, MAY 2019 1 Inviwo — A Visualization System with Usage Abstraction Levels Daniel Jonsson,¨ Peter Steneteg, Erik Sunden,´ Rickard Englund, Sathish Kottravel, Martin Falk, Member, IEEE, Anders Ynnerman, Ingrid Hotz, and Timo Ropinski Member, IEEE, Abstract—The complexity of today’s visualization applications demands specific visualization systems tailored for the development of these applications. Frequently, such systems utilize levels of abstraction to improve the application development process, for instance by providing a data flow network editor. Unfortunately, these abstractions result in several issues, which need to be circumvented through an abstraction-centered system design. Often, a high level of abstraction hides low level details, which makes it difficult to directly access the underlying computing platform, which would be important to achieve an optimal performance. Therefore, we propose a layer structure developed for modern and sustainable visualization systems allowing developers to interact with all contained abstraction levels. We refer to this interaction capabilities as usage abstraction levels, since we target application developers with various levels of experience. We formulate the requirements for such a system, derive the desired architecture, and present how the concepts have been exemplary realized within the Inviwo visualization system. Furthermore, we address several specific challenges that arise during the realization of such a layered architecture, such as communication between different computing platforms, performance centered encapsulation, as well as layer-independent development by supporting cross layer documentation and debugging capabilities. Index Terms—Visualization systems, data visualization, visual analytics, data analysis, computer graphics, image processing. F 1 INTRODUCTION The field of visualization is maturing, and a shift can be employing different layers of abstraction.
    [Show full text]
  • A Process for Digitizing and Simulating Biologically Realistic Oligocellular Networks Demonstrated for the Neuro-Glio-Vascular Ensemble Edited By: Yu-Guo Yu, Jay S
    fnins-12-00664 September 27, 2018 Time: 15:25 # 1 METHODS published: 25 September 2018 doi: 10.3389/fnins.2018.00664 A Process for Digitizing and Simulating Biologically Realistic Oligocellular Networks Demonstrated for the Neuro-Glio-Vascular Ensemble Edited by: Yu-Guo Yu, Jay S. Coggan1 †, Corrado Calì2 †, Daniel Keller1, Marco Agus3,4, Daniya Boges2, Fudan University, China * * Marwan Abdellah1, Kalpana Kare2, Heikki Lehväslaiho2,5, Stefan Eilemann1, Reviewed by: Renaud Blaise Jolivet6,7, Markus Hadwiger3, Henry Markram1, Felix Schürmann1 and Clare Howarth, Pierre J. Magistretti2 University of Sheffield, United Kingdom 1 Blue Brain Project, École Polytechnique Fédérale de Lausanne (EPFL), Geneva, Switzerland, 2 Biological and Environmental Ying Wu, Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 3 Visual Xi’an Jiaotong University, China Computing Center, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 4 CRS4, Center of Research *Correspondence: and Advanced Studies in Sardinia, Visual Computing, Pula, Italy, 5 CSC – IT Center for Science, Espoo, Finland, Jay S. Coggan 6 Département de Physique Nucléaire et Corpusculaire, University of Geneva, Geneva, Switzerland, 7 The European jay.coggan@epfl.ch; Organization for Nuclear Research, Geneva, Switzerland [email protected] Corrado Calì [email protected]; One will not understand the brain without an integrated exploration of structure and [email protected] function, these attributes being two sides of the same coin: together they form the †These authors share first authorship currency of biological computation. Accordingly, biologically realistic models require the re-creation of the architecture of the cellular components in which biochemical reactions Specialty section: This article was submitted to are contained.
    [Show full text]
  • IUS 2020 Table of Contents
    IUS 2020 Table of Contents IUS 2020 Table of Contents .................................................................................................................................1 IUS 2020 Patrons & Sponsor ..............................................................................................................................2 IUS 2020 Short Courses .......................................................................................................................................5 IUS 2020 Opening/Closing Events ....................................................................................................................7 IUS 2020 Live Social/Workshop Events ...........................................................................................................7 Technical Program Table of Contents .......................................................................................................... 14 1 IUS 2020 Patrons & Sponsor Platinum Patron Verasonics designs and markets leading-edge Vantage™ ultrasound research systems for academic and commercial investigators. These real-time, software-based, programmable ultrasound systems accelerate research by providing unsurpassed speed and control to simplify the data collection and analysis process. Researchers in 34 countries routinely use the unparalleled flexibility of the Vantage platform to advance the art and science of ultrasound through their own research efforts. In addition, to protect your investment and encompass additional research options, every Vantage
    [Show full text]
  • Direct Volume Rendering with Nonparametric Models of Uncertainty
    Direct Volume Rendering with Nonparametric Models of Uncertainty Tushar Athawale, Bo Ma, Elham Sakhaee, Chris R. Johnson, Fellow, IEEE, and Alireza Entezari, Senior Member, IEEE Fig. 1. Nonparametric models of uncertainty improve the quality of reconstruction and classification within an uncertainty-aware direct volume rendering framework. (a) Improvements in topology of an isosurface in the teardrop dataset (64 × 64 × 64) with uncertainty due to sampling and quantization. (b) Improvements in classification (i.e., bones in gray and kidneys in red) of the torso dataset with uncertainty due to downsampling. Abstract—We present a nonparametric statistical framework for the quantification, analysis, and propagation of data uncertainty in direct volume rendering (DVR). The state-of-the-art statistical DVR framework allows for preserving the transfer function (TF) of the ground truth function when visualizing uncertain data; however, the existing framework is restricted to parametric models of uncertainty. In this paper, we address the limitations of the existing DVR framework by extending the DVR framework for nonparametric distributions. We exploit the quantile interpolation technique to derive probability distributions representing uncertainty in viewing-ray sample intensities in closed form, which allows for accurate and efficient computation. We evaluate our proposed nonparametric statistical models through qualitative and quantitative comparisons with the mean-field and parametric statistical models, such as uniform and Gaussian, as well as Gaussian mixtures. In addition, we present an extension of the state-of-the-art rendering parametric framework to 2D TFs for improved DVR classifications. We show the applicability of our uncertainty quantification framework to ensemble, downsampled, and bivariate versions of scalar field datasets.
    [Show full text]
  • Medline-Sourced Journals Are Indicated in Green) Print-ISSN E-ISSN
    Sourcerecord id Source Title (Medline-sourced journals are indicated in Green) Print-ISSN E-ISSN 18500162600 21st Century Music 15343219 21100404576 2D Materials 20531583 21100447128 3 Biotech 2190572X 21905738 21100779062 3D Printing and Additive Manufacturing 23297662 23297670 21100229836 3D Research 20926731 19700200922 3L: Language, Linguistics, Literature 01285157 145295 4OR 16194500 16142411 16400154734 A + U-Architecture and Urbanism 03899160 5700161051 A Contrario 16607880 21100399164 A&A case reports 23257237 21100881366 A&A practice 25753126 19600162043 A.M.A. American Journal of Diseases of Children 00968994 19400157806 A.M.A. archives of dermatology 00965359 19600162081 A.M.A. Archives of Dermatology and Syphilology 00965979 19400157807 A.M.A. archives of industrial health 05673933 19600162082 A.M.A. Archives of Industrial Hygiene and Occupational Medicine 00966703 19400157808 A.M.A. archives of internal medicine 08882479 19400158171 A.M.A. archives of neurology 03758540 19400157809 A.M.A. archives of neurology and psychiatry 00966886 19400157810 A.M.A. archives of ophthalmology 00966339 19400157811 A.M.A. archives of otolaryngology 00966894 19400157812 A.M.A. archives of pathology 00966711 19400157813 A.M.A. archives of surgery 00966908 21100456161 a/b: Auto/Biography Studies 21517290 11600153683 A|Z ITU Journal of Faculty of Architecture 13028324 21100780699 A+BE Architecture and the Built Environment 22123202 22147233 5800207606 AAA, Arbeiten aus Anglistik und Amerikanistik 01715410 28033 AAC: Augmentative and Alternative
    [Show full text]
  • Medical and Volume Visualization SIGGRAPH 2015
    Medical and Volume Visualization SIGGRAPH 2015 Nicholas Polys, PhD & Michael Aratow, MD, FACEP Web3D Consortium www.web3d.org Medical WG Chairs Ander Arbelaiz, Luis Kabongo, Aitor Moreno Vicomtech-IK4 Darrell Hurt, Meaghan Coakley, James Terwitt-Drake National Institute of Health (NIH) Daniel Evestedt, Sebastian Ullrich Sensegraphics Update ! Web3D 2015 Annual Conference • Sponsored by ACM SIGGRAPH • in Cooperation with Web3D Consortium and Eurographics • 20th Annual held in Heraklion, Crete June 2015 – See papers @ siggraph.org and acm dl! • Next year in Anaheim co-located with SIGGRAPH Medical and Volume Visualization - X3D highlights - X3DOM (X3D + HTML5 + WebGL) Consortium • Content is King ! – Author and deploy interactive 3D assets and environments with confidence, royalty-free – Required: Portability, Interoperability, Durability • Not-for-profit, member-driven organization • International community of creators, developers, and users building evolving over 20 years of graphics and web technologies • Open Standards ratification (ISO/IEC) Medical and Volume Visualization The Web3D Consortium Medical Working Group is chartered to advance open 3D communication in the healthcare enterprise • BOFs, workshops, and progress since 2008 when TATRC sparked the flame with ISO/IEC Volume Component in X3D PUBLIC WIKI: http://www.web3d.org/wiki/index.php/X3D_Medical Web3D.org Medical Working Group • Reproducible rendering and presentations for stakeholders throughout the healthcare enterprise (and at home): – Structured and interactive virtual
    [Show full text]
  • Visflow - Web-Based Visualization Framework for Tabular Data with a Subset Flow Model
    VisFlow - Web-based Visualization Framework for Tabular Data with a Subset Flow Model Bowen Yu and Claudio´ T. Silva Fellow, IEEE Fig. 1. An overview of VisFlow. The user edits the VisFlow data flow diagram that corresponds to an interactive visualization web application in the VisMode. The model years of the user selected outliers in the scatterplot (b) are used to find all car models designed in those years (1981, 1982), which form a subset S that is visualized in three metaphors: a table for displaying row details (i), a histogram for horsepower distribution (j) and a heatmap for multi-dimensional visualization (k). The selected outliers are highlighted in red in the downflow of (b). The user selection in the parallel coordinates are brushed in blue and unified with S to be shown in (i), (j), (k). A heterogeneous table that contains the MDS coordinates of the cars are loaded in (l) and visualized in the MDS plot (q), with S being visually linked in yellow color among the other cars. Abstract— Data flow systems allow the user to design a flow diagram that specifies the relations between system components which process, filter or visually present the data. Visualization systems may benefit from user-defined data flows as an analysis typically consists of rendering multiple plots on demand and performing different types of interactive queries across coordinated views. In this paper, we propose VisFlow, a web-based visualization framework for tabular data that employs a specific type of data flow model called the subset flow model. VisFlow focuses on interactive queries within the data flow, overcoming the limitation of interactivity from past computational data flow systems.
    [Show full text]
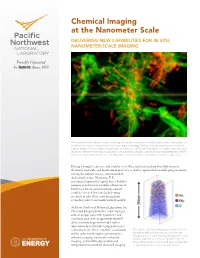
  • Chemical Imaging at the Nanometer Scale Delivering New Capabilities for in Situ, Nanometer-Scale Imaging
    Chemical Imaging at the Nanometer Scale DELIVERING NEW CAPABILITIES FOR IN SITU, NANOMETER-ScALE IMAGING The majority of microbes in natural and engineered environments live within structured communities or biofilms (seen here using confocal laser scanning microscopy). Biofilms include a poorly characterized organic matrix, termed extracellular polymeric substance (EPS), which facilitates certain biogeochemical reactions. We are enhancing visualization, compositional analysis, and functional characterization of EPS to better understand its influence on subsurface reactions vital to environmental and energy issues. Having a complete, precise, and realistic view of the molecular interactions that occur in chemical, materials, and biochemical processes is vital to exponential scientific progress and to solving the nation’s energy, environmental, and security issues. Numerous U.S. government-sponsored reports have identified imaging as critical for scientific advancement. However, current instrumentation cannot reach the needed level of clarity, leaving scientists to infer what is occurring from secondary sources and mathematical models. At Pacific Northwest National Laboratory, the Chemical Imaging Initiative is developing a suite of unique tools with nanometer-scale resolution and element specificity that will allow scientists to go from model system observation to real-world manipulation on a molecular level. These real-time, in situ tools Through the Chemical Imaging Initiative at Pacific will be achieved through near-nanometer Northwest
    [Show full text]
  • Low Wnt/B-Catenin Signaling Determines Leaky Vessels in The
    RESEARCH ARTICLE Low wnt/b-catenin signaling determines leaky vessels in the subfornical organ and affects water homeostasis in mice Fabienne Benz1, Viraya Wichitnaowarat1, Martin Lehmann1, Raoul FV Germano2, Diana Mihova1, Jadranka Macas1, Ralf H Adams3, M Mark Taketo4, Karl-Heinz Plate1,5,6,7,8, Sylvaine Gue´ rit1, Benoit Vanhollebeke2,9, Stefan Liebner1,5,6* 1Institute of Neurology (Edinger Institute), University Hospital, Goethe University Frankfurt, Frankfurt am Main, Germany; 2Laboratory of Neurovascular Signaling, Department of Molecular Biology, ULB Neuroscience Institute, Universite´ libre de Bruxelles, Bruxelles, Belgium; 3Department of Tissue Morphogenesis, Max-Planck- Institute for Molecular Biomedicine, University of Mu¨ nster, Faculty of Medicine, Mu¨ nster, Germany; 4Division of Experimental Therapeutics, Graduate School of Medicine, Kyoto University, Kyoto, Japan; 5Excellence Cluster Cardio-Pulmonary systems (ECCPS), Partner site Frankfurt, Frankfurt, Germany; 6German Cancer Consortium (DKTK), Partner Site Frankfurt/Mainz, Frankfurt, Germany; 7German Center for Cardiovascular Research (DZHK), Partner site Frankfurt/Mainz, Frankfurt, Germany; 8German Cancer Research Center (DKFZ), Heidelberg, Germany; 9Walloon Excellence in Life Sciences and Biotechnology (WELBIO), Wallonia, Belgium Abstract The circumventricular organs (CVOs) in the central nervous system (CNS) lack a vascular blood-brain barrier (BBB), creating communication sites for sensory or secretory neurons, involved in body homeostasis. Wnt/b-catenin signaling is essential for BBB development and *For correspondence: [email protected] maintenance in endothelial cells (ECs) in most CNS vessels. Here we show that in mouse development, as well as in adult mouse and zebrafish, CVO ECs rendered Wnt-reporter negative, Competing interests: The suggesting low level pathway activity. Characterization of the subfornical organ (SFO) vasculature authors declare that no revealed heterogenous claudin-5 (Cldn5) and Plvap/Meca32 expression indicative for tight and competing interests exist.
    [Show full text]