DOCSLIB.ORG

Geometry Vocabulary Word Wall Cards

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry Vocabulary Word Wall Cards Geometry Vocabulary Word Wall Cards Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development. The cards should be used as an instructional tool for teachers and then as a reference for all students. Table of Contents Reasoning, Lines, and Slope of Lines in Coordinate Plane Distance Formula Transformations Line Symmetry (Examples) Basics of Geometry 1 Point Symmetry (Examples) Basics of Geometry 2 Rotation (Origin) Geometry Notation Reflection Logic Notation Translation Set Notation Dilation Conditional Statement Perpendicular Bisector Converse Constructions: Inverse o A line segment congruent to a given line Contrapositive segment Symbolic Representations in Logical Arguments o Perpendicular bisector of a line segment Conditional Statements and Venn Diagrams o A perpendicular to a given line from a point Deductive Reasoning not on the line Inductive Reasoning o A perpendicular to a given line at a point on Direct Proofs the line Properties of Congruence o A bisector of an angle Law of Detachment o An angle congruent to a given angle Law of Syllogism o A line parallel to a given line through a Counterexample point not on the given line Perpendicular Lines o An equilateral triangle inscribed in a circle Parallel Lines o A square inscribed in a circle Skew Lines o A regular hexagon inscribed in a circle Transversal Corresponding Angles Triangles Alternate Interior Angles Classifying Triangles by Sides Alternate Exterior Angles Classifying Triangles by Angles Consecutive Interior Angles Triangle Sum Theorem Parallel Lines Exterior Angle Theorem Midpoint (definition) Pythagorean Theorem Midpoint Formula Angle and Sides Relationships Find a Missing Endpoint Triangle Inequality Theorem Slope Formula Virginia Department of Education 2018 Geometry Mathematics Vocabulary Congruent Triangles Isosceles Trapezoid SSS Triangle Congruence Postulate Circle SAS Triangle Congruence Postulate Circles – Inscribed HL Right Triangle Congruence Circle Equation ASA Triangle Congruence Postulate Lines and Circles AAS Triangle Congruence Theorem Secant Similar Polygons Tangent Similar Polygons and Proportions Central Angle AA Triangle Similarity Postulate Measuring Arcs SAS Triangle Similarity Theorem Arc Length SSS Triangle Similarity Theorem Secants and Tangents Altitude of a Triangle Inscribed Angle Median of a Triangle Area of a Sector Concurrency of Medians of a Triangle Inscribed Angle Theorem 1 30°-60°-90° Triangle Theorem Inscribed Angle Theorem 2 45°-45°-90° Triangle Theorem Inscribed Angle Theorem 3 Trigonometric Ratios Segments in a Circle Inverse Trigonometric Ratios Segments of Secants Theorem Area of a Triangle Segment of Secants and Tangents Theorem Polygons and Circles Three-Dimensional Figures Polygon Exterior Angle Sum Theorem Cone Polygon Interior Angle Sum Theorem Cylinder Regular Polygon Polyhedron Properties of Parallelograms Similar Solids Theorem Rectangle Sphere Rhombus Hemisphere Square Pyramid Trapezoid Virginia Department of Education 2018 Geometry Mathematics Vocabulary Basics of Geometry 1 Point – A point has no dimension. P It is a location on a plane. It is represented by a dot. point P Line – A line has one dimension. It is an infinite set of points represented by a line with two arrowheads that extend without end. m A B AB or BA or line m Plane – A plane has two dimensions extending without end. It is often represented by a parallelogram. N A plane ABC or plane N C B Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 1 Basics of Geometry 2 Line segment – A line segment consists of two endpoints and all the points between them. A B AB or BA Ray – A ray has one endpoint and extends without end in one direction. C BC B Note: Name the endpoint first. BC and CB are different rays. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 2 Geometry Notation Symbols used to represent statements or operations in geometry. BC segment BC BC ray BC BC line BC BC length of BC ABC angle ABC m measure of angle ABC ABC triangle ABC || is parallel to is perpendicular to is congruent to is similar to Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 3 Logic Notation ⋁ or ⋀ and → read “implies”, if… then… ↔ read “if and only if” iff read “if and only if” ~ not ∴ therefore Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 4 Set Notation { } empty set, null set ∅ empty set, null set x| read “x such that” x: read “x such that” ⋃ union, disjunction, or ⋂ intersection, conjunction, and Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 5 Conditional Statement a logical argument consisting of a set of premises, hypothesis (p), and conclusion (q) hypothesis If an angle is a right angle, then its measure is 90. conclusion Symbolically: if p, then q p→q Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 6 Converse formed by interchanging the hypothesis and conclusion of a conditional statement Conditional: If an angle is a right angle, then its measure is 90. Converse: If an angle measures 90, then the angle is a right angle. Symbolically: if q, then p q→p Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 7 Inverse formed by negating the hypothesis and conclusion of a conditional statement Conditional: If an angle is a right angle, then its measure is 90. Inverse: If an angle is not a right angle, then its measure is not 90. Symbolically: if ~p, then ~q ~p→~q Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 8 Contrapositive formed by interchanging and negating the hypothesis and conclusion of a conditional statement Conditional: If an angle is a right angle, then its measure is 90. Contrapositive: If an angle does not measure 90, then the angle is not a right angle. Symbolically: if ~q, then ~p ~q→~p Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 9 Symbolic Representations in Logical Arguments Conditional if p, then q p→q Converse if q, then p q→p if not p, Inverse ~p→~q then not q if not q, Contrapositive ~q→~p then not p Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 10 Conditional Statements and Venn Diagrams Original Conditional Statement Converse - Reversing the Clauses If an animal is a dolphin, If an animal is a mammal, then then it is a mammal. it is a dolphin. mammal dolphin dolphin mammal True! False! (Counterexample: An elephant is a mammal but is not a dolphin) Inverse - Negating the Clauses Contrapositive - Reversing and Negating the Clauses If an animal is not a dolphin, If an animal is not a mammal, then it is not a mammal. then it is not a dolphin. not mammal not dolphin not False! dolphin True! not (Counterexample: A mammal whale is not a dolphin but is still a mammal) Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 11 Deductive Reasoning method using logic to draw conclusions based upon definitions, postulates, and theorems Example of Deductive Reasoning: Statement A: If a quadrilateral contains only right angles, then it is a rectangle. Statement B: Quadrilateral P contains only right angles. Conclusion: Quadrilateral P is a rectangle. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 12 Inductive Reasoning method of drawing conclusions from a limited set of observations Example: Given a pattern, determine the next figure (set of dots) using inductive reasoning. Figure 1 Figure 2 Figure 3 The next figure should look like this: Figure 4 Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 13 Direct Proofs a justification logically valid and based on initial assumptions, definitions, postulates, and theorems Example: (two-column proof) Given: 1 2 Prove: 2 1 Statements Reasons 1 2 Given m1 = m2 Definition of congruent angles m2 = m1 Symmetric Property of Equality 2 1 Definition of congruent angles Example: (paragraph proof) It is given that 1≅2. By the Definition of congruent angles, m 1 = m2. By the Symmetric Property of Equality, m2 = m1. By the Definition of congruent angles, 2≅1. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 14 Properties of Congruence 퐴퐵̅̅̅̅ 퐴퐵̅̅̅̅ Reflexive Property ∠퐴 ≅ ∠퐴 If 퐴퐵̅̅̅̅ ≅ ̅퐶퐷̅̅̅ , then ̅퐶퐷̅̅̅ ≅ 퐴퐵̅̅̅̅. Symmetric Property If ∠퐴 ≅ ∠퐵, then ∠퐵 ≅ ∠퐴 If 퐴퐵̅̅̅̅ ≅ ̅퐶퐷̅̅̅ and ̅퐶퐷̅̅̅ ≅ 퐸퐹̅̅̅̅, then 퐴퐵̅̅̅̅ ≅ 퐸퐹̅̅̅̅. Transitive Property If ∠퐴 ≅ ∠퐵 푎푛푑 ∠퐵 ≅ ∠퐶, then ∠퐴 ≅ ∠퐶. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 15 Law of Detachment deductive reasoning stating that if the hypothesis of a true conditional statement is true then the conclusion is also true 120 A Example: If mA > 90°, then A is an obtuse angle mA = 120 Therefore, A is an obtuse angle. If pq is a true conditional statement and p is true, then q is true. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 16 Law of Syllogism deductive reasoning that draws a new conclusion from two conditional statements when the conclusion of one is the hypothesis of the other Example: 1. If a rectangle has four congruent sides, then it is a square. 2. If a polygon is a square, then it is a regular polygon. 3. If a rectangle has four congruent sides, then it is a regular polygon. If pq and qr are true conditional statements, then pr is true. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 17 Counterexample specific case for which a conjecture is false Example: Conjecture: “The product of any two numbers is odd.” Counterexample: 2 ∙ 3 = 6 One counterexample proves a conjecture false. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 18 Perpendicular Lines two lines that intersect to form a right angle m n Line m is perpendicular to line n. m n Perpendicular lines have slopes that are negative reciprocals. Virginia Department of Education 2018 Geometry Mathematics Vocabulary – Card 19 Parallel Lines coplanar lines that do not intersect m n m||n Line m is parallel to line n.
Load more

Recommended publications
  • Section 5.5 Right Triangle Trigonometry 385
    Section 5.5 Right Triangle Trigonometry 385 Section 5.5 Right Triangle Trigonometry In section 5.3 we were introduced to the sine and cosine function as ratios of the sides of a triangle drawn inside a circle, and spent the rest of that section discussing the role of those functions in finding points on the circle. In this section, we return to the triangle, and explore the applications of the trigonometric functions to right triangles where circles may not be involved. Recall that we defined sine and cosine as (x, y) y sin( θ ) = r r y x cos( θ ) = θ r x Separating the triangle from the circle, we can make equivalent but more general definitions of the sine, cosine, and tangent on a right triangle. On the right triangle, we will label the hypotenuse as well as the side opposite the angle and the side adjacent (next to) the angle. Right Triangle Relationships Given a right triangle with an angle of θ opposite sin( θ) = hypotenuse hypotenuse opposite adjacent cos( θ) = hypotenuse θ opposite adjacent tan( θ) = adjacent A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.” 386 Chapter 5 Example 1 Given the triangle shown, find the value for cos( α) . The side adjacent to the angle is 15, and the 17 hypotenuse of the triangle is 17, so 8 adjacent 15 cos( α) = = α hypotenuse 17 15 When working with general right triangles, the same rules apply regardless of the orientation of the triangle.
    [Show full text]
  • Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1
    Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1. Acute angle: Angle whose measure is greater than 0° and less than 90°. 2. Adjacent angles: Two angles that have a common side and a common vertex. 3. Alternate interior angles: A pair of angles in the interior of a figure formed by two lines and a transversal, lying on alternate sides of the transversal and having different vertices. 4. Altitude: Perpendicular segment from a vertex of a triangle to the opposite side or the line containing the opposite side. 5. Angle: A figure formed by two rays with a common endpoint. 6. Angle bisector: Ray that divides an angle into two congruent angles and bisects the angle. 7. Base Angles: Two angles not included in the legs of an isosceles triangle. 8. Bisect: To divide a segment or an angle into two congruent parts. 9. Coincide: To lie on top of the other. A line can coincide another line. 10. Collinear: Lying on the same line. 11. Complimentary: Two angle’s whose sum is 90°. 12. Concave Polygon: Polygon in which at least one interior angle measures more than 180° (at least one segment connecting two vertices is outside the polygon). 13. Conclusion: A result of summary of all the work that has been completed. The part of a conditional statement that occurs after the word “then”. 14. Congruent parts: Two or more parts that only have the same measure. In CPCTC, the parts of the congruent triangles are congruent. 15. Congruent triangles: Two triangles are congruent if and only if all of their corresponding parts are congruent.
    [Show full text]
  • Properties of Equidiagonal Quadrilaterals (2014)
    Forum Geometricorum Volume 14 (2014) 129–144. FORUM GEOM ISSN 1534-1178 Properties of Equidiagonal Quadrilaterals Martin Josefsson Abstract. We prove eight necessary and sufficient conditions for a convex quadri- lateral to have congruent diagonals, and one dual connection between equidiag- onal and orthodiagonal quadrilaterals. Quadrilaterals with both congruent and perpendicular diagonals are also discussed, including a proposal for what they may be called and how to calculate their area in several ways. Finally we derive a cubic equation for calculating the lengths of the congruent diagonals. 1. Introduction One class of quadrilaterals that have received little interest in the geometrical literature are the equidiagonal quadrilaterals. They are defined to be quadrilat- erals with congruent diagonals. Three well known special cases of them are the isosceles trapezoid, the rectangle and the square, but there are other as well. Fur- thermore, there exists many equidiagonal quadrilaterals that besides congruent di- agonals have no special properties. Take any convex quadrilateral ABCD and move the vertex D along the line BD into a position D such that AC = BD. Then ABCD is an equidiagonal quadrilateral (see Figure 1). C D D A B Figure 1. An equidiagonal quadrilateral ABCD Before we begin to study equidiagonal quadrilaterals, let us define our notations. In a convex quadrilateral ABCD, the sides are labeled a = AB, b = BC, c = CD and d = DA, and the diagonals are p = AC and q = BD. We use θ for the angle between the diagonals. The line segments connecting the midpoints of opposite sides of a quadrilateral are called the bimedians and are denoted m and n, where m connects the midpoints of the sides a and c.
    [Show full text]
  • Geometrygeometry
    Park Forest Math Team Meet #3 GeometryGeometry Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. Geometry: Angle measures in plane figures including supplements and complements 3. Number Theory: Divisibility rules, factors, primes, composites 4. Arithmetic: Order of operations; mean, median, mode; rounding; statistics 5. Algebra: Simplifying and evaluating expressions; solving equations with 1 unknown including identities Important Information you need to know about GEOMETRY… Properties of Polygons, Pythagorean Theorem Formulas for Polygons where n means the number of sides: • Exterior Angle Measurement of a Regular Polygon: 360÷n • Sum of Interior Angles: 180(n – 2) • Interior Angle Measurement of a regular polygon: • An interior angle and an exterior angle of a regular polygon always add up to 180° Interior angle Exterior angle Diagonals of a Polygon where n stands for the number of vertices (which is equal to the number of sides): • • A diagonal is a segment that connects one vertex of a polygon to another vertex that is not directly next to it. The dashed lines represent some of the diagonals of this pentagon. Pythagorean Theorem • a2 + b2 = c2 • a and b are the legs of the triangle and c is the hypotenuse (the side opposite the right angle) c a b • Common Right triangles are ones with sides 3, 4, 5, with sides 5, 12, 13, with sides 7, 24, 25, and multiples thereof—Memorize these! Category 2 50th anniversary edition Geometry 26 Y Meet #3 - January, 2014 W 1) How many cm long is segment 6 XY ? All measurements are in centimeters (cm).
    [Show full text]
  • Right Triangles and the Pythagorean Theorem Related?
    Activity Assess 9-6 EXPLORE & REASON Right Triangles and Consider △​ ABC​ with altitude ​​CD‾ ​​ as shown. the Pythagorean B Theorem D PearsonRealize.com A 45 C 5√2 I CAN… prove the Pythagorean Theorem using A. What is the area of △​ ​ABC? ​Of △​ACD? Explain your answers. similarity and establish the relationships in special right B. Find the lengths of ​​AD‾ ​​ and ​​AB‾ ​​. triangles. C. Look for Relationships Divide the length of the hypotenuse of △​ ABC​ VOCABULARY by the length of one of its sides. Divide the length of the hypotenuse of ​ △ACD​ by the length of one of its sides. Make a conjecture that explains • Pythagorean triple the results. ESSENTIAL QUESTION How are similarity in right triangles and the Pythagorean Theorem related? Remember that the Pythagorean Theorem and its converse describe how the side lengths of right triangles are related. THEOREM 9-8 Pythagorean Theorem If a triangle is a right triangle, If... ​△ABC​ is a right triangle. then the sum of the squares of the B lengths of the legs is equal to the square of the length of the hypotenuse. c a A C b 2 2 2 PROOF: SEE EXAMPLE 1. Then... ​​a​​ ​ + ​b​​ ​ = ​c​​ ​ THEOREM 9-9 Converse of the Pythagorean Theorem 2 2 2 If the sum of the squares of the If... ​​a​​ ​ + ​b​​ ​ = ​c​​ ​ lengths of two sides of a triangle is B equal to the square of the length of the third side, then the triangle is a right triangle. c a A C b PROOF: SEE EXERCISE 17. Then... ​△ABC​ is a right triangle.
    [Show full text]
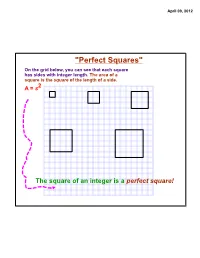
  • "Perfect Squares" on the Grid Below, You Can See That Each Square Has Sides with Integer Length
    April 09, 2012 "Perfect Squares" On the grid below, you can see that each square has sides with integer length. The area of a square is the square of the length of a side. A = s2 The square of an integer is a perfect square! April 09, 2012 Square Roots and Irrational Numbers The inverse of squaring a number is finding a square root. The square-root radical, , indicates the nonnegative square root of a number. The number underneath the square root (radical) sign is called the radicand. Ex: 16 = 121 = 49 = 144 = The square of an integer results in a perfect square. Since squaring a number is multiplying it by itself, there are two integer values that will result in the same perfect square: the positive integer and its opposite. 2 Ex: If x = (perfect square), solutions would be x and (-x)!! Ex: a2 = 25 5 and -5 would make this equation true! April 09, 2012 If an integer is NOT a perfect square, its square root is irrational!!! Remember that an irrational number has a decimal form that is non- terminating, non-repeating, and thus cannot be written as a fraction. For an integer that is not a perfect square, you can estimate its square root on a number line. Ex: 8 Since 22 = 4, and 32 = 9, 8 would fall between integers 2 and 3 on a number line. -2 -1 0 1 2 3 4 5 April 09, 2012 Approximate where √40 falls on the number line: Approximate where √192 falls on the number line: April 09, 2012 Topic Extension: Simplest Radical Form Simplify the radicand so that it has no more perfect-square factors.
    [Show full text]
  • Introduction to Geometry" ©2014 Aops Inc
    Excerpt from "Introduction to Geometry" ©2014 AoPS Inc. www.artofproblemsolving.com CHAPTER 12. CIRCLES AND ANGLES (a) Consider the circle with diameter OP. Call this circle . Why must hit O in at least two di↵erent C C points? (b) Why is it impossible for to hit O in three di↵erent points? Hints: 530 C (c) Let the points where hits O be A and B. Prove that \PAO = \PBO = 90 . C ◦ (d) Prove that PA and PB are tangent to O. (e)? Now for the tricky part – proving that these are the only two tangents. Suppose D is on O such that PD is tangent to O. Why must D be on ? Hints: 478 C (f) Why does the previous part tell us that PA! and PB! are the only lines through P tangent to O? 12.3.6? O is tangent to all four sides of rhombus ABCD, AC = 24, and AB = 15. (a) Prove that AC and BD meet at O (i.e., prove that the intersection of the diagonals of ABCD is the center of the circle.) Hints: 439 (b) What is the area of O? Hints: 508 12.4 Problems Problems Problem 12.19: A quadrilateral is said to be a cyclic quadrilateral if a circle can be drawn that passes through all four of its vertices. Prove that if ABCD is a cyclic quadrilateral, then \A + \C = 180◦. C Problem 12.20: In the figure, PC is tangent to the circle and PD 70◦ bisects \CPE. Furthermore, CD = 70◦, DE = 50◦, and \DQE = P B Q D 40◦.
    [Show full text]
  • Midsegment of a Trapezoid Parallelogram
    Vocabulary Flash Cards base angles of a trapezoid bases of a trapezoid Chapter 7 (p. 402) Chapter 7 (p. 402) diagonal equiangular polygon Chapter 7 (p. 364) Chapter 7 (p. 365) equilateral polygon isosceles trapezoid Chapter 7 (p. 365) Chapter 7 (p. 402) kite legs of a trapezoid Chapter 7 (p. 405) Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards The parallel sides of a trapezoid Either pair of consecutive angles whose common side is a base of a trapezoid A polygon in which all angles are congruent A segment that joins two nonconsecutive vertices of a polygon A trapezoid with congruent legs A polygon in which all sides are congruent The nonparallel sides of a trapezoid A quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards midsegment of a trapezoid parallelogram Chapter 7 (p. 404) Chapter 7 (p. 372) rectangle regular polygon Chapter 7 (p. 392) Chapter 7 (p. 365) rhombus square Chapter 7 (p. 392) Chapter 7 (p. 392) trapezoid Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards A quadrilateral with both pairs of opposite sides The segment that connects the midpoints of the parallel legs of a trapezoid PQRS A convex polygon that is both equilateral and A parallelogram with four right angles equiangular A parallelogram with four congruent sides and four A parallelogram with four congruent sides right angles A quadrilateral with exactly one pair of parallel sides Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved.
    [Show full text]
  • Cyclic Quadrilaterals
    GI_PAGES19-42 3/13/03 7:02 PM Page 1 Cyclic Quadrilaterals Definition: Cyclic quadrilateral—a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage™ 200 with Cabri screen, and label its center O. Using the Polygon tool, construct quadrilateral ABCD where A, B, C, and D are on circle O. By the definition given Figure 1 above, ABCD is a cyclic quadrilateral (Figure 1). Cyclic quadrilaterals have many interesting and surprising properties. Use the Voyage 200 with Cabri tools to investigate the properties of cyclic quadrilateral ABCD. See whether you can discover several relationships that appear to be true regardless of the size of the circle or the location of A, B, C, and D on the circle. 2. Measure the lengths of the sides and diagonals of quadrilateral ABCD. See whether you can discover a relationship that is always true of these six measurements for all cyclic quadrilaterals. This relationship has been known for 1800 years and is called Ptolemy’s Theorem after Alexandrian mathematician Claudius Ptolemaeus (A.D. 85 to 165). 3. Determine which quadrilaterals from the quadrilateral hierarchy can be cyclic quadrilaterals (Figure 2). 4. Over 1300 years ago, the Hindu mathematician Brahmagupta discovered that the area of a cyclic Figure 2 quadrilateral can be determined by the formula: A = (s – a)(s – b)(s – c)(s – d) where a, b, c, and d are the lengths of the sides of the a + b + c + d quadrilateral and s is the semiperimeter given by s = 2 . Using cyclic quadrilaterals, verify these relationships.
    [Show full text]
  • Cyclic and Bicentric Quadrilaterals G
    Cyclic and Bicentric Quadrilaterals G. T. Springer Email: [email protected] Hewlett-Packard Calculators and Educational Software Abstract. In this hands-on workshop, participants will use the HP Prime graphing calculator and its dynamic geometry app to explore some of the many properties of cyclic and bicentric quadrilaterals. The workshop will start with a brief introduction to the HP Prime and an overview of its features to get novice participants oriented. Participants will then use ready-to-hand constructions of cyclic and bicentric quadrilaterals to explore. Part 1: Cyclic Quadrilaterals The instructor will send you an HP Prime app called CyclicQuad for this part of the activity. A cyclic quadrilateral is a convex quadrilateral that has a circumscribed circle. 1. Press ! to open the App Library and select the CyclicQuad app. The construction consists DEGH, a cyclic quadrilateral circumscribed by circle A. 2. Tap and drag any of the points D, E, G, or H to change the quadrilateral. Which of the following can DEGH never be? • Square • Rhombus (non-square) • Rectangle (non-square) • Parallelogram (non-rhombus) • Isosceles trapezoid • Kite Just move the points of the quadrilateral around enough to convince yourself for each one. Notice HDE and HE are both inscribed angles that subtend the entirety of the circle; ≮ ≮ likewise with DHG and DEG. This leads us to a defining characteristic of cyclic ≮ ≮ quadrilaterals. Make a conjecture. A quadrilateral is cyclic if and only if… 3. Make DEGH into a kite, similar to that shown to the right. Tap segment HE and press E to select it. Now use U and D to move the diagonal vertically.
    [Show full text]
  • Math 1330 - Section 4.1 Special Triangles
    Math 1330 - Section 4.1 Special Triangles In this section, we’ll work with some special triangles before moving on to defining the six trigonometric functions. Two special triangles are 30 − 60 − 90 triangles and 45 − 45 − 90 triangles. With little additional information, you should be able to find the lengths of all sides of one of these special triangles. First we’ll review some conventions when working with triangles. We label angles with capital letters and sides with lower case letters. We’ll use the same letter to refer to an angle and the side opposite it, although the angle will be a capital letter and the side will be lower case. In this section, we will work with right triangles. Right triangles have one angle which measures 90 degrees, and two other angles whose sum is 90 degrees. The side opposite the right angle is called the hypotenuse, and the other two sides are called the legs of the triangle. A labeled right triangle is shown below. B c a A C b Recall: When you are working with a right triangle, you can use the Pythagorean Theorem to help you find the length of an unknown side. In a right triangle ABC with right angle C, 2 2 2 a + b = c . Example: In right triangle ABC with right angle C, if AB = 12 and AC = 8, find BC. 1 Special Triangles In a 30 − 60 − 90 triangle, the lengths of the sides are proportional. If the shorter leg (the side opposite the 30 degree angle) has length a, then the longer leg has length 3a and the hypotenuse has length 2a.
    [Show full text]
  • Isosceles Triangles on a Geoboard
    Isosceles Triangles on a Geoboard About Illustrations: Illustrations of the Standards for Mathematical Practice (SMP) consist of several pieces, including a mathematics task, student dialogue, mathematical overview, teacher reflection questions, and student materials. While the primary use of Illustrations is for teacher learning about the SMP, some components may be used in the classroom with students. These include the mathematics task, student dialogue, and student materials. For additional Illustrations or to learn about a professional development curriculum centered around the use of Illustrations, please visit mathpractices.edc.org. About the Isosceles Triangles on a Geoboard Illustration: This Illustration’s student dialogue shows the conversation among three students who are looking for how many isosceles triangles can be constructed on a geoboard given only one side. After exploring several cases where the known side is one of the congruent legs, students then use the known side as the base and make an interesting observation. Highlighted Standard(s) for Mathematical Practice (MP) MP 1: Make sense of problems and persevere in solving them. MP 5: Use appropriate tools strategically. MP 7: Look for and make use of structure. Target Grade Level: Grades 6–7 Target Content Domain: Geometry Highlighted Standard(s) for Mathematical Content 7.G.A.2 Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. Math Topic Keywords: isosceles triangles, geoboard © 2016 by Education Development Center. Isosceles Triangles on a Geoboard is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
    [Show full text]