Information to Users
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1. the ZK User Interface Markup Language
1. The ZK User Interface Markup Language The ZK User Interface Markup Language (ZUML) is based on XML. Each XML element describes what component to create. XML This section provides the most basic concepts of XML to work with ZK. If you are familiar with XML, you could skip this section. If you want to learn more, there are a lot of resources on Internet, such as http://www.w3schools.com/xml/xml_whatis.asp and http://www.xml.com/pub/a/98/10/guide0.html. XML is a markup language much like HTML but with stricter and cleaner syntax. It has several characteristics worth to notice. Elements Must Be Well-formed First, each element must be closed. They are two ways to close an element as depicted below. They are equivalent. Close by an end tag: <window></window> Close without an end tag: <window/> Second, elements must be properly nested. Correct: <window> <groupbox> Hello World! </groupbox> </window> Wrong: <window> <groupbox> Hello World! </window> </groupbox> Special Character Must Be Replaced XML uses <element-name> to denote an element, so you have to replace special characters. For example, you have to use < to represent the < character. ZK: Developer's Guide Page 1 of 92 Potix Corporation Special Character Replaced With < < > > & & " " ' ' It is interesting to notice that backslash (\) is not a special character, so you don't need to escape it at all. Attribute Values Must Be Specified and Quoted Correct: width="100%" checked="true" Wrong: width=100% checked Comments A comment is used to leave a note or to temporarily edit out a portion of XML code. -

ZKTM Mobile for Android the Quick Start Guide
ppoottiixx SIMPLY REACH ZKTM Mobile for Android The Quick Start Guide Version 0.8.1 Feburary 2008 Potix Corporation ZK Mobile for Android for Android: Quick Start Guide Page 1 of 14 Potix Corporation Copyright © Potix Corporation. All rights reserved. The material in this document is for information only and is subject to change without notice. While reasonable efforts have been made to assure its accuracy, Potix Corporation assumes no liability resulting from errors or omissions in this document, or from the use of the information contained herein. Potix Corporation may have patents, patent applications, copyright or other intellectual property rights covering the subject matter of this document. The furnishing of this document does not give you any license to these patents, copyrights or other intellectual property. Potix Corporation reserves the right to make changes in the product design without reservation and without notification to its users. The Potix logo and ZK are trademarks of Potix Corporation. All other product names are trademarks, registered trademarks, or trade names of their respective owners. ZK Mobile for Android for Android: Quick Start Guide Page 2 of 14 Potix Corporation Table of Contents Before You Start.............................................................................................................. 4 New to ZK Framework.....................................................................................................4 New to Google Android....................................................................................................4 -

Dictionary Software Based on Ajax Frameworks
Seminar Paper Dictionary Software based on Ajax Frameworks Matthias Kerstner Institute for Information Systems and Computer Media Graz University of Technology Head: Herman Maurer O.Univ.-Prof. Dr.Dr.h.c.mult. Supervisor: Denis Helic Dipl.-Ing. Dr.techn. September 2007 Seminar Paper Abstract Abstract The necessity for dictionaries cannot be disputed. Although there are a vast variety of them they all follow a basic schema a key-value combination. It is interesting to see that many of the well known dictionary producers recently also provide electronic versions of their products, ranging from CDROMs over USB media to online databases. With the event of Ajax, web-based applications can be turned into desktop-like environments. It provides developers with an effective way to build web-applications using existing facilities (browsers, etc.), while still profiting from the latest technology. Seminar Paper Contents Contents Abstract ............................................................................................................3 Contents ...........................................................................................................4 List of Figures...................................................................................................5 1. Introduction ...............................................................................................6 2. Dictionaries ...............................................................................................8 3. Ajax Frameworks ......................................................................................9 -

Comparing Javascript Libraries
www.XenCraft.com Comparing JavaScript Libraries Craig Cummings, Tex Texin October 27, 2015 Abstract Which JavaScript library is best for international deployment? This session presents the results of several years of investigation of features of JavaScript libraries and their suitability for international markets. We will show how the libraries were evaluated and compare the results for ECMA, Dojo, jQuery Globalize, Closure, iLib, ibm-js and intl.js. The results may surprise you and will be useful to anyone designing new international or multilingual JavaScript applications or supporting existing ones. 2 Agenda • Background • Evaluation Criteria • Libraries • Results • Q&A 3 Origins • Project to extend globalization - Complex e-Commerce Software - Multiple subsystems - Different development teams - Different libraries already in use • Should we standardize? Which one? - Reduce maintenance - Increase competence 4 Evaluation Criteria • Support for target and future markets • Number of internationalization features • Quality of internationalization features • Maintained? • Widely used? • Ease of migration from existing libraries • Browser compatibility 5 Internationalization Feature Requirements • Encoding Support • Text Support -Unicode -Case, Accent Mapping -Supplementary Chars -Boundary detection -Bidi algorithm, shaping -Character Properties -Transliteration -Charset detection • Message Formatting -Conversion -IDN/IRI -Resource/properties files -Normalization -Collation -Plurals, Gender, et al 6 Internationalization Feature Requirements -

RIA Mit ZK Boost Your Productivity
RIA mit ZK Boost your productivity Daniel Seiler, AIA 2008, Mainz Agenda Introduction ZK basics ZK component library We build an application ZK advanced concepts Custom component example Integration example, Gmaps Summary Goals of this session Infect you with the ZK virus You are able to explain the position of ZK in the current RIA Landscape You know the main features, concepts and principles of ZK Daniel Seiler, Processwide AG 3 The problem to solve To build rich, interactive, fast and scalable, distributed business applications ... ... we need a framework and technology that ... ... maximizes our productivity by abstracting and hiding much of the complexity ... provides a rich set of prebuilt components and features ... is easy to extend Daniel Seiler, Processwide AG 4 The big picture Local offline Trad. Distributed Rich (Asynchronous update, sorting, drag & drop, ...) Trad. Web- tools applications applications I nternet (Communication with Webserver) (Standalone, not ('Fat client', corba, RMI, (Page reloading, distributed, ...) local installation, ...) Application (User interactions, data storage, ...) simple controls) Office tools Eclipse RCP Runs in an external Runs directly in a runtime environment browser (No plugin, (plugin or standalone) Ajax) Applets (Java) Javascript Framework Flex (flash) library Laszlo (flash) Curl Captain Casa jQuery Echo2 (Swing, JSF) Prototype GWT Script.aculo.us ICE Faces DWR ZK Daniel Seiler, Processwide AG 5 The right tool for your job R ichness + Rich UI Local offline - Local, no central access -

RIA with ZK Boost Your Productivity
RIA with ZK Boost your productivity Daniel Seiler AdNovum Informatik AG Submission Id: 7960 2 AGENDA > Introduction > ZK basics > Lets build an application > Advanced topics > Custom components > Some more examples > ZK and the others > What's coming next? > Summary > Q & A Goals Infect you with the ZK virus You are able to explain the position of ZK in the current RIA Landscape You know the main features, concepts and principles of ZK The problem to solve To build rich, interactive, fast and scalable, distributed business applications ... ... we need a framework and technology that ... ... maximizes our productivity by abstracting and hiding much of the complexity ... provides a rich set of prebuilt components and features ... is easy to extend The big picture Local offline “Fat Client” Rich (Async. update, sorting, drag & drop) Trad. web tools Distributed I nternet (Communication with Webserver) applications (Standalone, not applications (Page reloading, distributed, ...) (Corba, RMI, WS , ...) Application (User interactions, data storage) simple controls) Office tools Eclipse RCP Runs in an external Runs directly in a runtime environment browser (No plugin, Ajax) (plugin or standalone) Java FX Flex (flash) Javascript Frameworks Laszlo (flash) libraries Curl Echo2 Captain Casa jQuery GWT (Swing, JSF) Prototype ICE Faces Script.aculo.us IT Mill vaadin DWR ZK What is ZK? From Wikipedia: http://en.wikipedia.org/wiki/ZK_Framework ZK is an open-source Ajax web application framework, written in Java, that enables creation of rich graphical user interfaces for web applications with no JavaScript and little programming knowledge. The core of ZK consists of an Ajax-based event-driven mechanism, over 123 XUL and 83 XHTML-based components, and a markup language for designing user interfaces. -

The Libx Edition Builder
The LibX Edition Builder Tilottama Gaat Thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master of Science in Computer Science and Applications Godmar Back, Chair Edward Fox, Committee Member Eli Tilevich, Committee Member 23 July, 2008 Blacksburg, Virginia Keywords: LibX, AJAX, Code Generation, Log-based usability evaluation Copyright 2008, Tilottama Gaat The LibX Edition Builder Tilottama Gaat ABSTRACT LibX is a browser plugin that allows users to access library resources directly from their browser. Many libraries that wished to adopt LibX needed to customize a version of LibX for their own institution. Most librarians did not possess the necessary knowledge of XML, running scripts and the underlying implementation of LibX required to create customized, functional LibX versions for their own institutions. Therefore, we have developed a web- based tool called the LibX Edition Builder that empowers librarians to create their own customized LibX versions (editions), effortlessly. The Edition Builder provides rich interactivity to its users by exploiting the ZK AJAX framework whose components we adapted. The Edition Builder provides automatic detec- tion of relevant library resources based on several heuristics which we have developed, which reduces the time and effort required to configure these resources. We have used sound software engineering techniques such as agile development principles, code generation techniques, and the model-view-controller design paradigm to maximize maintainability of the Edition Builder, which enables us to easily incorporate changing func- tional requirements in the Edition Builder. The LibX Edition Builder is currently used by over 800 registered users who have created over 400 editions. -
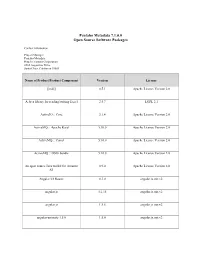
Pentaho Metadata 7.1.0.0 Open Source Software Packages
Pentaho Metadata 7.1.0.0 Open Source Software Packages Contact Information: Project Manager Pentaho Metadata Hitachi Vantara Corporation 2535 Augustine Drive Santa Clara, California 95054 Name of Product/Product Component Version License [ini4j] 0.5.1 Apache License Version 2.0 A Java library for reading/writing Excel 2.5.7 LGPL 2.1 ActiveIO :: Core 3.1.4 Apache License Version 2.0 ActiveMQ :: Apache Karaf 5.10.0 Apache License Version 2.0 ActiveMQ :: Camel 5.10.0 Apache License Version 2.0 ActiveMQ :: OSGi bundle 5.10.0 Apache License Version 2.0 An open source Java toolkit for Amazon 0.9.0 Apache License Version 2.0 S3 Angular UI Router 0.3.0 angular.js.mit.v2 angular.js 1.2.15 angular.js.mit.v2 angular.js 1.5.8 angular.js.mit.v2 angular-animate-1.5.6 1.5.6 angular.js.mit.v2 Name of Product/Product Component Version License angular-route 1.5.6 angular.js.mit.v2 angular-sanitize-1.5.6 1.5.6 angular.js.mit.v2 angular-translate 2.3.0 angular.js.mit.v2 angular-translate-2.12.1 2.12.1 angular.bootstrap.mit.v2 angular-translate-2.12.1 2.12.1 angular.js.mit.v2 AngularUI Bootstrap 0.6.0 angular.bootstrap.mit.v2 AngularUI Bootstrap 1.3.3 angular.bootstrap.mit.v2 Annotation 1.0 1.1.1 Apache License Version 2.0 Annotation 1.1 1.0.1 Apache License Version 2.0 ANTLR 3 Complete 3.5.2 ANTLR License Antlr 3.4 Runtime 3.4 ANTLR License ANTLR, ANother Tool for Language 2.7.7 ANTLR License Recognition AOP Alliance (Java/J2EE AOP standard) 1.0 Public Domain Apache Ant Core 1.9.1 Apache License Version 2.0 Name of Product/Product Component Version License -

Ajax and Web 2.0 Related Frameworks and Toolkits Dennis Chen Director of Product Engineering / Potix Corporation [email protected]
Ajax and Web 2.0 Related Frameworks and Toolkits Dennis Chen Director of Product Engineering / Potix Corporation [email protected] 1 Agenda • Ajax Introduction • Access Server Side (Java) API/Data/Service > jQuery + DWR > GWT > ZK • Summary 2 AJAX INTRODUCTION 3 What is Ajax • Asynchronous JavaScript and XML • Browser asynchronously get data from a server and update page dynamically without refreshing(reloading) the whole page • Web Application Development Techniques > DHTML, CSS (Cascade Style Sheet) > Javascript and HTML DOM > Asynchronous XMLHttpRequest 4 Traditional Web Application vs. Ajax within a browser, there is AJAX engine 5 Ajax Interaction Example Demo 6 Challenge of Providing Ajax • Technique Issue > JavaScript , DHTML and CSS • Cross Browser Issue > IE 6,7,8 , Firefox 2,3 , Safari 3, Opera 9, Google Chrome… • Asynchronous Event and Data • Business Logic and Security • Maintenance 7 Solutions : Ajax Frameworks / Toolkits • Client Side Toolkit > jQuery, Prototype , … • Client Side Framework > GWT ,YUI, Ext-JS, Dojo … • Server Side Toolkit (Java) > DWR… • Server Side Framwork > ZK, ECHO2, ICEface .. 8 JQUERY + DWR 9 What is jQuery • http://jquery.com/ • A JavaScript toolkit that simplifies the interaction between HTML and JavaScript. • Lightweight and Client only • Provides high level function to > Simplify DOM access and alternation > Enable multiple handlers per event > Add effects/animations > Asynchronous interactions with server • Solve browser incompatibilities 10 Powerful Selector / Traversing API • Powerful Selector -

ZKTM the Quick Start Guide
ppoottiixx SIMPLY RICH ZKTM The Quick Start Guide Version 3.0.4 March 2008 Potix Corporation ZK: Quick Start Guide Page 1 of 16 Potix Corporation Copyright © Potix Corporation. All rights reserved. The material in this document is for information only and is subject to change without notice. While reasonable efforts have been made to assure its accuracy, Potix Corporation assumes no liability resulting from errors or omissions in this document, or from the use of the information contained herein. Potix Corporation may have patents, patent applications, copyright or other intellectual property rights covering the subject matter of this document. The furnishing of this document does not give you any license to these patents, copyrights or other intellectual property. Potix Corporation reserves the right to make changes in the product design without reservation and without notification to its users. The Potix logo and ZK are trademarks of Potix Corporation. All other product names are trademarks, registered trademarks, or trade names of their respective owners. ZK: Quick Start Guide Page 2 of 16 Potix Corporation Table of Contents Before You Start.............................................................................................................. 4 New to the Servlet Container (aka., Java Web Server)........................................................ 4 New to Java Language.................................................................................................... 4 New to Java Integrated Development Environment (IDE)................................................... -

Checklist: Requirements GUI Test Tool for Java, Web
GUI-Testtool for Java, Web & native Windows Applications ✓ The Tool for Professional UI Test Automation Features Java applications: Swing, JavaFX, AWT, SWT, Eclipse Plug-Ins, RCP, Applets, JavaWebStart, RIA, ULC, CaptainCasa, JavaFX SubScene Components Web applications: Browsers: Chrome, Firefox, Opera, Safari, Edge (Chromium based), Microsoft Edge Legacy, Internet Explorer; Headless Browser Versions of Chrome, Firefox and Edge (Chromium based) HTML 5, AJAX: QF-Test completely supports frameworks like Angular, React and Vue.js and also other UI-toolkits like GWT, Smart GWT, ExtGWT, ExtJS, ICEfaces, jQueryUI, jQueryEasyUI, KendoUI, PrimeFaces, Qooxdoo, GUI-technology of the RAP, RichFaces, Vaadin and ZK. Further toolkits can be integrated with little application under test effort e.g. SAP UI5, Siebel Open UI and Salesforce. Testing of Electron and Webswing applications is supported as well. Windows applications: classic Win32, .NET (often developed with C#), Windows Presentation Foundation (WPF), Windows Forms, Windows Apps / Universal Windows Platform (UWP) with XAML control elements, modern C++ applications (e.g. with Qt) Hybrid systems with the combination of multiple GUI technologies, as well as embedded browser components (JavaFX WebView, JXBrowser, SWT- Browser) PDF documents can be tested like a normal application (textual and graphical checks for individual elements) Java applications: Swing and JavaFX: Windows, Linux, Unix, macOS GUI support depending SWT: Windows, Linux-GTK; Solaris-GTK upon request on operating system Web applications: Windows, Linux, macOS Windows applications: Windows Capturing function (Capture/Replay) for direct and efficient generation of test sequences for further processing into more complex test cases with Testing principle flow control, parameterization, modularization and extended scripting possibilities. Everything can be customized. -

Pentaho Reporting 7.1.0.0 Open Source Software Packages
Pentaho Reporting 7.1.0.0 Open Source Software Packages Contact Information: Project Manager Pentaho Reporting Hitachi Vantara Corporation 2535 Augustine Drive Santa Clara, California 95054 Name of Product/Product Version License Component [ini4j] 0.5.1 Apache License Version 2.0 ActiveIO :: Core 3.1.4 Apache License Version 2.0 ActiveMQ :: Apache Karaf 5.10.0 Apache License Version 2.0 ActiveMQ :: Camel 5.10.0 Apache License Version 2.0 ActiveMQ :: OSGi bundle 5.10.0 Apache License Version 2.0 akka-actor 2.3.3 Apache License Version 2.0 An open source Java toolkit for 0.9.0 Apache License Version 2.0 Amazon S3 Angular UI Router 0.3.0 angular.js.mit.v2 angular.js 1.5.6 angular.js.mit.v2 angular.js 1.5.8 angular.js.mit.v2 angular-route 1.5.6 angular.js.mit.v2 Name of Product/Product Version License Component angular-sanitize-1.5.6 1.5.6 angular.js.mit.v2 angular-translate-2.12.1 2.12.1 angular.js.mit.v2 AngularUI Bootstrap 0.10.0 angular.bootstrap.mit.v2 Annotation 1.0 1.1.1 Apache License Version 2.0 Annotation 1.1 1.0.1 Apache License Version 2.0 ANTLR 3 Complete 3.5.2 ANTLR License Antlr 3.4 Runtime 3.4 ANTLR License ANTLR, ANother Tool for Language 2.7.7 ANTLR License Recognition AOP Alliance (Java/J2EE AOP 1.0 Public Domain standard) Apache ActiveMQ 5.2.0 Apache License Version 2.0 Apache Ant Core 1.9.1 Apache License Version 2.0 Apache Ant Launcher 1.9.1 Apache License Version 2.0 Apache Aries Blueprint API 1.0.1 Apache License Version 2.0 Apache Aries Blueprint CM 1.0.5 Apache License Version 2.0 Name of Product/Product Version