DOCSLIB.ORG

Chapter 7: from Theory to Observations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 7: from Theory to Observations Chapter 7: From theory to observations Given the stellar mass and chemical composition of a ZAMS, the stellar modeling can, in principle, predict the evolution of the stellar bolometric luminosity, effective temperature Teff , and possibly even the surface chemical composition. How can these parameters be linked to observables? Outline Spectra and magnitudes The effects of interstellar extinction K-correction for high-redshift objects Spectroscopic notation of the stellar chemical composition Calibration and uncertainty Review Spectra and magnitudes One important way is the use of the Color Magnitude Diagram (CMD), which is the observational counterpart of the HRD. HRD of selected stellar evolutionary tracks CMD of the globular cluster M3 using the (dashed lines) with the same initial solar Johnson BV filters. Remember that the chemical composition. The heavy solid magnitude scale is backward wrt intensity; lines display two isochrones for the same a larger value of B − V implies a cool chemical composition and ages of 600 Myr object. (the brighter sequence) and 10 Gyr. Magnitude definition The apparent magnitude is defined as R fλSλdλ 0 mA ≡ −2:5log R 0 + mA fλ Sλdλ where fλ is the monochromatic flux (or spectrum) of a star received at 0 the top of the Earth’s atmosphere while fλ denotes the spectrum of a 0 reference star that produces a known apparent magnitude mA, which is called the ’zero point’ of the band for a given photometric system. I This system specifies a specific choice of the response function, Sλ. I Many photometric systems exist! I Measured magnitudes do depend on both the fλ and the actual photometric system used (i.e., the shape of the filter). I So in general, one should not compare magnitudes defined for different photometric systems. Various photometric systems The very popular Johnson system, for example, uses the star Vega (A0V at the distance of 7.7 pc; M = 2:14M ) to fix the zero points. It assumes that mV = 0 and that the color indices are equal to zero for the star, whereas other systems may have slightly different values. The absolute magnitude is defined as the apparent magnitude a star would have at a distance of 10 pc (if the radiation travels undisturbed from the source to the observer): " # d 2 R f S dλ M ≡ −2:5log λ λ + m0 = m − 5(log(d) − 1) A R 0 A A 10 pc fλSλdλ where d is the distance in parsec. In the cosmological context, the distance is so called luminosity distance dL. mA − MA ≡ (m − M)A is called the distance modulus. What do you think about a comparison of this Mbol value with MK ; = 3:4? The absolute bolometric magnitude is independent of any photometry system! Absolute bolometric magnitude The absolute magnitude of the Sun is then " 2 R # d f S dλ M ≡ −2:5log λ, λ + m0 : A; R 0 A 10 pc fλSλdλ By setting Sλ = 1 at all wavelengths in the above two definitions (thus the subscript change from A to bol ) and adopting the Sun as the reference star (placing it at the distance of 10 pc), we have the definition of the absolute bolometric magnitude of a star as Mbol ≡ Mbol; − 2:5log(L=L ) 33 −1 where L = 3:826 × 10 ergs s and Mbol; = 4:75. The absolute bolometric magnitude is independent of any photometry system! Absolute bolometric magnitude The absolute magnitude of the Sun is then " 2 R # d f S dλ M ≡ −2:5log λ, λ + m0 : A; R 0 A 10 pc fλSλdλ By setting Sλ = 1 at all wavelengths in the above two definitions (thus the subscript change from A to bol ) and adopting the Sun as the reference star (placing it at the distance of 10 pc), we have the definition of the absolute bolometric magnitude of a star as Mbol ≡ Mbol; − 2:5log(L=L ) 33 −1 where L = 3:826 × 10 ergs s and Mbol; = 4:75. What do you think about a comparison of this Mbol value with MK ; = 3:4? Absolute bolometric magnitude The absolute magnitude of the Sun is then " 2 R # d f S dλ M ≡ −2:5log λ, λ + m0 : A; R 0 A 10 pc fλSλdλ By setting Sλ = 1 at all wavelengths in the above two definitions (thus the subscript change from A to bol ) and adopting the Sun as the reference star (placing it at the distance of 10 pc), we have the definition of the absolute bolometric magnitude of a star as Mbol ≡ Mbol; − 2:5log(L=L ) 33 −1 where L = 3:826 × 10 ergs s and Mbol; = 4:75. What do you think about a comparison of this Mbol value with MK ; = 3:4? The absolute bolometric magnitude is independent of any photometry system! Observationally, one needs to select proper filters that are Evolution of a 1 M star with Z = 0:001 sensitive to the desirable and Y = 0:246 from the ZAMS until the tip of the RGB, displayed in the HRD and measurements, particular for Teff . various CMDs. Bolometric correction The bolometric correction to a given photometric band A is defined as BCA ≡ Mbol − MA: If the stellar bolometric luminosity is known (from a model), one can predict the corresponding MA. In practice, tables of bolometric corrections and color indices are available, for a grid of gravities and Teff that cover all the major phases of stellar evolution, and for a number of chemical compositions. Interpolations among the grid points provide the sought BCA for the model. Bolometric correction The bolometric correction to a given photometric band A is defined as BCA ≡ Mbol − MA: If the stellar bolometric luminosity is known (from a model), one can predict the corresponding MA. In practice, tables of bolometric corrections and color indices are available, for a grid of gravities and Teff that cover all the major phases of stellar evolution, and for a number of chemical compositions. Interpolations among the grid points provide the sought BCA for the model. Observationally, one needs to select proper filters that are Evolution of a 1 M star with Z = 0:001 sensitive to the desirable and Y = 0:246 from the ZAMS until the tip of the RGB, displayed in the HRD and measurements, particular for Teff . various CMDs. Outline Spectra and magnitudes The effects of interstellar extinction K-correction for high-redshift objects Spectroscopic notation of the stellar chemical composition Calibration and uncertainty Review With this extinction-corrected magnitude, mA;0, together with the distance module, we can then calculate the absolute magnitude, A (= MA). The effect of extinction on a color index (A − B) is (A − B) = (A − B)0 + E(A − B) where E(A − B) = AA − AB is called the color excess or reddening. The effects of interstellar extinction If the extinction (Aλ) is important, the observed flux is then −τλ −0:4Aλ fλ = fλ,0e ≡ fλ,010 Defining AA as R −0:4Aλ −0:4A 10 fλ,0Sλdλ 10 A ≡ R ; fλ,0Sλdλ assuming certain Aλ and fλ,0 (as functions of λ), we have mA = mA;0 + AA: The effect of extinction on a color index (A − B) is (A − B) = (A − B)0 + E(A − B) where E(A − B) = AA − AB is called the color excess or reddening. The effects of interstellar extinction If the extinction (Aλ) is important, the observed flux is then −τλ −0:4Aλ fλ = fλ,0e ≡ fλ,010 Defining AA as R −0:4Aλ −0:4A 10 fλ,0Sλdλ 10 A ≡ R ; fλ,0Sλdλ assuming certain Aλ and fλ,0 (as functions of λ), we have mA = mA;0 + AA: With this extinction-corrected magnitude, mA;0, together with the distance module, we can then calculate the absolute magnitude, A (= MA). The effects of interstellar extinction If the extinction (Aλ) is important, the observed flux is then −τλ −0:4Aλ fλ = fλ,0e ≡ fλ,010 Defining AA as R −0:4Aλ −0:4A 10 fλ,0Sλdλ 10 A ≡ R ; fλ,0Sλdλ assuming certain Aλ and fλ,0 (as functions of λ), we have mA = mA;0 + AA: With this extinction-corrected magnitude, mA;0, together with the distance module, we can then calculate the absolute magnitude, A (= MA). The effect of extinction on a color index (A − B) is (A − B) = (A − B)0 + E(A − B) where E(A − B) = AA − AB is called the color excess or reddening. I The extinction law, Aλ=AV , is usually determined empirically, where AV is the extinction in the Johnson V band. Notice the 2175 A˚ bump. I The ratio RV ≡ AV =E(B − V ) is nearly a constant and equal to 3.1 for stars in the Galaxy. I More accurately, AV can be determined in a color-color plot, e.g., U − B vs. B − V . I For large reddening (e.g., toward the Galactic center), one needs to account for the non-constancy of Aλ and hence the substantial spectral change in a given filter range. Outline Spectra and magnitudes The effects of interstellar extinction K-correction for high-redshift objects Spectroscopic notation of the stellar chemical composition Calibration and uncertainty Review I One claim for the origin of the term ”K correction” is the correction as a Konstante (German for ”constant”) used by Carl Wirtz. I To determine the appropriate K-correction, one obviously needs to know the shape of the object intrinsic spectrum, or its evolution with time (e.g., related to the evolution of the stellar content, which may be modeled theoretically for a galaxy). K-correction for high-redshift objects I When an observing object (typically a galaxy) has a non-negligible redshift, one also needs to make the so-called K-correction, converting a measurement to an equivalent measurement in the rest frame of the object.
Load more

Recommended publications
  • Luminosity - Wikipedia
    12/2/2018 Luminosity - Wikipedia Luminosity In astronomy, luminosity is the total amount of energy emitted by a star, galaxy, or other astronomical object per unit time.[1] It is related to the brightness, which is the luminosity of an object in a given spectral region.[1] In SI units luminosity is measured in joules per second or watts. Values for luminosity are often given in the terms of the luminosity of the Sun, L⊙. Luminosity can also be given in terms of magnitude: the absolute bolometric magnitude (Mbol) of an object is a logarithmic measure of its total energy emission rate. Contents Measuring luminosity Stellar luminosity Image of galaxy NGC 4945 showing Radio luminosity the huge luminosity of the central few star clusters, suggesting there is an Magnitude AGN located in the center of the Luminosity formulae galaxy. Magnitude formulae See also References Further reading External links Measuring luminosity In astronomy, luminosity is the amount of electromagnetic energy a body radiates per unit of time.[2] When not qualified, the term "luminosity" means bolometric luminosity, which is measured either in the SI units, watts, or in terms of solar luminosities (L☉). A bolometer is the instrument used to measure radiant energy over a wide band by absorption and measurement of heating. A star also radiates neutrinos, which carry off some energy (about 2% in the case of our Sun), contributing to the star's total luminosity.[3] The IAU has defined a nominal solar luminosity of 3.828 × 102 6 W to promote publication of consistent and comparable values in units of https://en.wikipedia.org/wiki/Luminosity 1/9 12/2/2018 Luminosity - Wikipedia the solar luminosity.[4] While bolometers do exist, they cannot be used to measure even the apparent brightness of a star because they are insufficiently sensitive across the electromagnetic spectrum and because most wavelengths do not reach the surface of the Earth.
    [Show full text]
  • Diameter and Photospheric Structures of Canopus from AMBER/VLTI Interferometry,
    A&A 489, L5–L8 (2008) Astronomy DOI: 10.1051/0004-6361:200810450 & c ESO 2008 Astrophysics Letter to the Editor Diameter and photospheric structures of Canopus from AMBER/VLTI interferometry, A. Domiciano de Souza1, P. Bendjoya1,F.Vakili1, F. Millour2, and R. G. Petrov1 1 Lab. H. Fizeau, CNRS UMR 6525, Univ. de Nice-Sophia Antipolis, Obs. de la Côte d’Azur, Parc Valrose, 06108 Nice, France e-mail: [email protected] 2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany Received 23 June 2008 / Accepted 25 July 2008 ABSTRACT Context. Direct measurements of fundamental parameters and photospheric structures of post-main-sequence intermediate-mass stars are required for a deeper understanding of their evolution. Aims. Based on near-IR long-baseline interferometry we aim to resolve the stellar surface of the F0 supergiant star Canopus, and to precisely measure its angular diameter and related physical parameters. Methods. We used the AMBER/VLTI instrument to record interferometric data on Canopus: visibilities and closure phases in the H and K bands with a spectral resolution of 35. The available baselines (60−110 m) and the high quality of the AMBER/VLTI observations allowed us to measure fringe visibilities as far as in the third visibility lobe. Results. We determined an angular diameter of / = 6.93 ± 0.15 mas by adopting a linearly limb-darkened disk model. From this angular diameter and Hipparcos distance we derived a stellar radius R = 71.4 ± 4.0 R. Depending on bolometric fluxes existing in the literature, the measured / provides two estimates of the effective temperature: Teff = 7284 ± 107 K and Teff = 7582 ± 252 K.
    [Show full text]
  • On the Zero Point Constant of the Bolometric Correction Scale
    MNRAS 000, 1–12 () Preprint 8 March 2021 Compiled using MNRAS LATEX style file v3.0 On the Zero Point Constant of the Bolometric Correction Scale Z. Eker 1?, V. Bakış1, F. Soydugan2;3 and S. Bilir4 1Akdeniz University, Faculty of Sciences, Department of Space Sciences and Technologies, 07058, Antalya, Turkey 2Department of Physics, Faculty of Arts and Sciences, Çanakkale Onsekiz Mart University, 17100 Çanakkale, Turkey 3Astrophysics Research Center and Ulupınar Observatory, Çanakkale Onsekiz Mart University, 17100, Çanakkale, Turkey 4Istanbul University, Faculty of Science, Department of Astronomy and Space Sciences, 34119, Istanbul, Turkey ABSTRACT Arbitrariness attributed to the zero point constant of the V band bolometric correc- tions (BCV ) and its relation to “bolometric magnitude of a star ought to be brighter than its visual magnitude” and “bolometric corrections must always be negative” was investigated. The falsehood of the second assertion became noticeable to us after IAU 2015 General Assembly Resolution B2, where the zero point constant of bolometric magnitude scale was decided to have a definite value CBol(W ) = 71:197 425 ::: . Since the zero point constant of the BCV scale could be written as C2 = CBol − CV , where CV is the zero point constant of the visual magnitudes in the basic definition BCV = MBol − MV = mbol − mV , and CBol > CV , the zero point constant (C2) of the BCV scale cannot be arbitrary anymore; rather, it must be a definite positive number obtained from the two definite positive numbers. The two conditions C2 > 0 and 0 < BCV < C2 are also sufficient for LV < L, a similar case to negative BCV numbers, which means that “bolometric corrections are not always negative”.
    [Show full text]
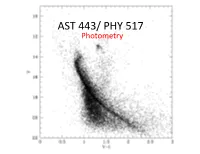
  • Photometry Rule of Thumb
    AST 443/ PHY 517 Photometry Rule of Thumb For a uniform flux distribution, V=0 corresponds to • 3.6 x 10-9 erg cm-2 s-1 A-1 (at 5500 A = 550 nm) • 996 photons cm-2 s-1 A-1 remember: E = hn = hc/l Basic Photometry The science of measuring the brightness of an astronomical object. In principle, it is straightforward; in practice (as in much of astronomy), there are many subtleties that can cause you great pains. For this course, you do not need to deal with most of these effects, but you should know about them (especially extinction). Among the details you should be acquainted with are: • Bandpasses • Magnitudes • Absolute Magnitudes • Bolometric Fluxes and Magnitudes • Colors • Atmospheric Extinction • Atmospheric Refraction • Sky Brightness • Absolute Photometry Your detector measures the flux S in a bandpass dw. 2 2 The units of the detected flux S are erg/cm /s/A (fλ) or erg/cm /s/Hz (fν). Bandpasses Set by: • detector response, • the filter response • telescope reflectivity • atmospheric transmission Basic types of filters: • long pass: transmit light longward of some fiducial wavelength. The name of the filter often gives the 50% transmission wavelength in nm. E.g, the GG495 filter transmits 50% of the incident light at 495 nm, and has higher transmission at longer wavelengths. • short pass: transmit light shortward of some fiducial wavelength. Examples are CuSO4 and BG38. • isolating: used to select particular bandpasses. May be made of a combination of long- and short-pass filters. Narrow band filters are generally interference filters. Broadband Filters • The Johnson U,B,V bands are standard.
    [Show full text]
  • Astronomy and Astrophysics
    A Problem book in Astronomy and Astrophysics Compilation of problems from International Olympiad in Astronomy and Astrophysics (2007-2012) Edited by: Aniket Sule on behalf of IOAA international board July 23, 2013 ii Copyright ©2007-2012 International Olympiad on Astronomy and Astrophysics (IOAA). All rights reserved. This compilation can be redistributed or translated freely for educational purpose in a non-commercial manner, with customary acknowledgement of IOAA. Original Problems by: academic committees of IOAAs held at: – Thailand (2007) – Indonesia (2008) – Iran (2009) – China (2010) – Poland (2011) – Brazil (2012) Compiled and Edited by: Aniket Sule Homi Bhabha Centre for Science Education Tata Institute of Fundamental Research V. N. Purav Road, Mankhurd, Mumbai, 400088, INDIA Contact: [email protected] Thank you! Editor would like to thank International Board of International Olympiad on Astronomy and Astrophysics (IOAA) and particularly, president of the board, Prof. Chatief Kunjaya, and general secretary, Prof. Gregorz Stachowaski, for entrusting this task to him. We acknowledge the hard work done by respec- tive year’s problem setters drawn from the host countries in designing the problems and fact that all the host countries of IOAA graciously agreed to permit use of the problems, for this book. All the members of the interna- tional board IOAA are thanked for their support and suggestions. All IOAA participants are thanked for their ingenious solutions for the problems some of which you will see in this book. iv Thank you! A Note about Problems You will find a code in bracket after each problem e.g. (I07 - T20 - C). The first number simply gives the year in which this problem was posed I07 means IOAA2007.
    [Show full text]
  • Model Atmospheres Broad-Band Colors, Bolometric Corrections and Temperature Calibrations Foro-Mstars?
    Astron. Astrophys. 333, 231–250 (1998) ASTRONOMY AND ASTROPHYSICS Model atmospheres broad-band colors, bolometric corrections and temperature calibrations forO-Mstars? M.S. Bessell1, F. Castelli2, and B. Plez3;4 1 Mount Stromlo and Siding Spring Observatories, Institute of Advanced Studies, The Australian National University, Weston Creek P.O., ACT 2611, Australia 2 CNR-Gruppo Nazionale Astronomia and Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, I-34131 Trieste, Italy 3 Astronomiska Observatoriet, Box 515, S-75120 Uppsala, Sweden 4 Atomspektroskopi, Fysiska Institution, Box 118, S-22100 Lund, Sweden Received 29 September 1997 / Accepted 3 December 1997 Abstract. Broad band colors and bolometric corrections in the luminosity (eg. bolometric corrections: Schmidt-Kaler 1982; Johnson-Cousins-Glass system (Bessell, 1990; Bessell & Brett, Reid & Gilmore 1984; Bessell & Wood 1984; Tinney et al. 1988) have been computed from synthetic spectra from new 1993; temperatures: Bessell 1979, 1995; Ridgway et al. 1980; model atmospheres of Kurucz (1995a), Castelli (1997), Plez, Di Benedetto & Rabbia 1987; Blackwell & Lynas-Gray 1994 Brett & Nordlund (1992), Plez (1995-97), and Brett (1995a,b). (BLG94); Tsuji et al. 1995, 1996a; Alonso et al. 1996 (AAM96); These atmospheres are representative of larger grids that are cur- Dyck et al. 1996; Perrin et al. 1997). However, apart from rently being completed. We discuss differences between the dif- AAM96 who give Teff - color relations for F0-K5 dwarfs with ferent grids and compare theoretical color-temperature relations both solar and lower than solar metallicity, these empirical data and the fundamental color temperature relations derived from: are mostly defined by a restricted group of stars, namely nearby (a) the infrared-flux method (IRFM) for A-K stars (Blackwell solar composition giants and dwarfs.
    [Show full text]
  • Measuring the Properties of Stars and Galaxies
    Measuring the properties of stars and galaxies See C&M Chap. 3 (radiation basics), 4 (spectral properties) and 17! Many properties of stars and galaxies are measured via our understanding of the interaction between light and matter. Please review chapter 3 if you need a refresher on what the electromagnetic spectrum is and what we mean by wavelength, frequency etc. Given a photon of enough energy, the electron can escape wheee! and the atom is ionized A more energetic (blue) photon is needed in order to excite an electron to higher orbits from the ground state (lowest energy level). Less energetic (red) photons are required for smaller jumps. long wavelength short wavelength Each element has a unique configuration of electron orbits, so its emission spectrum is unique. Estimating stellar temperatures A continuous spectrum emitted by an ideal non-reflecting surface is called blackbody radiation and has a very distinctive shape with total flux (energy per unit area per unit time, or power per area) given by the Stefan-Boltzmann law: F = σ T4 (σ is the Stefan Boltzmann constant = 5.67e-8 W/m2K4) The value of λmax and temperature are connected by Wien’s displacement law: 6 λmax (nm) = 2.9 x 10 Temperature (K) Example: Your body temperature is about 37 degrees centigrade, what is this in kelvin? At what wavelength do you emit most of your radiation? What part of the electromagnetic spectrum is this? Tkelvin = Tcentigrade + 273 = 37 + 273 = 310 K 6 λmax (nm) = 2.9 x 10 Temperature (K) = 2.9 x 106 = 9355 nm 310 1000 nm is the same a 1µm (1 micron), so 9355nm = 9.4 µm , which is in the infra-red.
    [Show full text]
  • Bolometric Correction for Brown Dwarfs
    Bolometric Correction for Brown Dwarfs Balaji Muthusubramanian & Johanna Hartke April 9, 2014 1 Scientific Justification Bolometric corrections are essential in estimating the absolute bolometric magnitude and luminosity of a source. The Bolometric correction for a photometric band is defined as the difference between absolute magnitude and the magnitude of the stellar/sub-stellar objects in that band. BCV = Mbol − MV (1) To correct for the bolometric magnitude, we need to employ a reference point. Generally, this reference point is taken as the Sun: Mbol; = MV; + BCV; = V + 31:572 + BCV; ; (2) where V is the apparent V band magnitude of the Sun.Thus the bolometric magnitude is computed as Mbol − Mbol; = −2:5log(L=L ): (3) Hence the V magnitude of the star can be corrected by combining equa- tions 1, 2 and 3 as, MV = −2:5log(L=L ) + V + 31:572 − (BCV − BCV; ) (4) We can adopt the solar parameters from Allen (2000) to be, MV; = 4:82, Mbol; = 4:74, BCv; = −0:08 and V = −26:75. Emperical relations for the V-band bolometric corrections have been computed by Flower (1996) and Torres (2010). Flower (1996) used a data sample of 335 stars to derive the following empirical relation between the Bolometric Correction and log(Teff ), 2 BCV = a + b log(Teff ) + c log(Teff ) + ::: (5) The coefficients were later corrected by Torres (2010). The coefficients for different ranges of log(Teff ) from Torres (2010) are given in table 1. 1 Table 1: Coefficients from (Torres 2010) Coefficient log(Teff ) > 3:90 3:90 > log(Teff ) > 3:70 log(Teff ) < 3:70 a 0.190537291496456E+05 0.370510203809015E+05 0.118115450538963E+06 b 0.155144866764412E+05 0.385672629965804E+05 0.137145973583929E+06 c 0.421278819301717E+04 0.150651486316025E+05 0.636233812100225E+05 d 0.381476328422343E+03 0.261724637119416E+04 0.147412923562646E+05 e ..
    [Show full text]
  • Universal Bolometric Corrections for Active Galactic Nuclei Over Seven Luminosity Decades F
    A&A 636, A73 (2020) Astronomy https://doi.org/10.1051/0004-6361/201936817 & c ESO 2020 Astrophysics Universal bolometric corrections for active galactic nuclei over seven luminosity decades F. Duras1,2,3 , A. Bongiorno2, F. Ricci4, E. Piconcelli2, F. Shankar5, E. Lusso6,7, S. Bianchi1, F. Fiore8,9, R. Maiolino10, A. Marconi6, F. Onori11, E. Sani12, R. Schneider13,2, C. Vignali14,15, and F. La Franca1 1 Dipartimento di Matematica e Fisica, Università Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy e-mail: [email protected] 2 Osservatorio Astronomico di Roma – INAF, Via Frascati 33, 00040 Monteporzio Catone, Italy 3 Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France 4 Instituto de Astrofísica and Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile 5 Department of Physics and Astronomy, University of Southampton, Highfield SO17 1BJ, UK 6 Dipartimento di Fisica e Astronomia, Università di Firenze, Via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy 7 Osservatorio Astrofisico di Arcetri – INAF, 50125 Firenze, Italy 8 Osservatorio Astronomico di Trieste – INAF, Via Tiepolo 11, 34143 Trieste, Italy 9 INAF – Osservatorio Astronomico di Trieste, Via G. Tiepolo 11, 34124 Trieste, Italy 10 Cavendish Laboratory, University of Cambridge, 19 J. J. Thomson Ave., Cambridge CB3 0HE, UK 11 Istituto di Astrofisica e Planetologia Spaziali (INAF), Via del Fosso del Cavaliere 100, Roma 00133, Italy 12 European Southern Observatory, Santiago, Chile 13 Dipartimento di Fisica, Università di Roma La Sapienza, 00185 Roma, Italy 14 Dipartimento di Fisica e Astronomia, Alma Mater Studiorum, Università degli Studi di Bologna, Via Gobetti 93/2, 40129 Bologna, Italy 15 Osservatorio di Astrofisica e Scienza dello Spazio di Bologna – INAF, Via Gobetti 93/3, 40129 Bologna, Italy Received 1 October 2019 / Accepted 24 January 2020 ABSTRACT Context.
    [Show full text]
  • Notes on Stars
    Page 1 I?M?P?R?S on ASTROPHYSICS at LMU Munich Astrophysics Introductory Course Lecture given by Ralf Bender in collaboration with: Chris Botzler, Andre Crusius-Watzel,¨ Niv Drory, Georg Feulner, Armin Gabasch, Ulrich Hopp, Claudia Maraston, Michael Matthias, Jan Snigula, Daniel Thomas Fall 2001 Astrophysics Introductory Course Fall 2001 Chapter 2 The Stars: Spectra and Fundamental Properties Astrophysics Introductory Course Fall 2001 Page 3 2.1 Magnitudes and all that ... The apparent magnitude m at frequency ν of an astronomical object is defined via: fν mν = −2.5 log fν(V ega) 2 with fν being the object’s flux (units of W/m /Hz). In this classical or Vega magnitude system Vega (α Lyrae), an A0V star (see below), is used as the reference star. In the Vega magnitude system, Vega has magnitude 0 at all frequencies. The logarithmic magnitude scale mimicks the intensity sensitivity of the human eye. It is defined in a way that it roughly reproduces the ancient Greek magnitude scale (0...6 = brightest... faintest stars visible by naked eye). Today, the AB-magnitude system is becoming increasingly popular. In the AB-system a source of constant fν has constant magnitude: f m = −2.5 log ν AB (3.6308 × 10−23W/Hz/m2) The normalizing flux is chosen in a such a way that Vega magnitudes and AB-magnitudes are the same at 5500A.˚ Astrophysics Introductory Course Fall 2001 Page 4 In most observations, the fluxes measured are not monochromatic but are integrated over a filter bandpass. Typical broad band filters have widths of several hundred to 2000A.˚ The magnitude for a filter x (Tx(ν) =transmission function) is then defined via: R fνTx(ν)dν mx = −2.5 log R fν,V egaTx(ν)dν Several filter systems were designed: Johnson UBVRIJHKLMN Kron-Cousins RCIC Stroemgrenu v b y Hβ Gunn ugriz Sloan Digitial Sky Survey filters: u0 g0 r0 i0 z0 , probably the standard of the future whereby U = near UV, B = blue, V = visual(green), R = red, I = near infrared, JHKLMN = infrared A typical precision which can be obtained relatively easily is: ∆m ∼ ∆fx/fx ∼ 0.02.
    [Show full text]
  • Fundamental Parameters and Spectral Energy Distributions Of
    Draft version August 10, 2015 Preprint typeset using LATEX style emulateapj v. 11/10/09 FUNDAMENTAL PARAMETERS AND SPECTRAL ENERGY DISTRIBUTIONS OF YOUNG AND FIELD AGE OBJECTS WITH MASSES SPANNING THE STELLAR TO PLANETARY REGIME Joseph C. Filippazzo1,2,3, Emily L. Rice1,2,3, Jacqueline Faherty2,5,6, Kelle L. Cruz2,3,4, Mollie M. Van Gordon7, Dagny L. Looper8 1Department of Engineering Science and Physics, College of Staten Island, City University of New York, 2800 Victory Blvd, Staten Island, NY 10314, USA 2Department of Astrophysics, American Museum of Natural History, New York, NY 10024, USA 3The Graduate Center, City University of New York, New York, NY 10016, USA 4Department of Physics and Astronomy, Hunter College, City University of New York, New York, NY 10065, USA 5Department of Terrestrial Magnetism, Carnegie Institution of Washington, DC 20015, USA 6Hubble Fellow 7Department of Geography, University of California, Berkeley, CA 94720, USA and 8Tisch School of the Arts, New York University, New York, NY 10003, USA Draft version August 10, 2015 ABSTRACT We combine optical, near-infrared and mid-infrared spectra and photometry to construct expanded spectral energy distributions (SEDs) for 145 field age (>500 Myr) and 53 young (lower age estimate <500 Myr) ultracool dwarfs (M6-T9). This range of spectral types includes very low mass stars, brown dwarfs, and planetary mass objects, providing fundamental parameters across both the hydrogen and deuterium burning minimum masses for the largest sample assembled to date. A subsample of 29 objects have well constrained ages as probable members of a nearby young moving group (NYMG).
    [Show full text]
  • Canopus Angular Diameter Revisited by the AMBER Instrument of the VLT Interferometer
    The 8th Pacific Rim Conference on Stellar Astrophysics ASP Conference Series, Vol. 404, c 2009 B. Soonthornthum, S. Komonjinda, K. S. Cheng, and K.-C. Leung, eds. Canopus Angular Diameter Revisited by the AMBER Instrument of the VLT Interferometer P. Bendjoya,1 A. Domiciano de Souza,1 F. Vakili,1 F. Millour,2 and R. Petrov1 Abstract. We used the VLTI/AMBER instrument to obtain interferometric data on the F0I star Canopus (visibilities and closure phases in the H and K bands with spectral resolution of 35). The adopted baselines (100 m) and the high quality of the VLTI/AMBER observations allowed us to measure fringe visibilities up to the third visibility lobe of Canopus.The angular diameter has been measured from the visibility and set to be (6.95 0.15) mas. From this measured angular diameter we derive a stellar radius R±= (72 4)R and an ± effective temperature Teff = (7272 107)K or Teff = (7570 250)K depending⊙ on the considered bolometric flux± and its precision. Contrarily± to the theory, our VLTI/AMBER data do not reveal any limb darkening on Canopus in the near-IR. Our observations set new constraints on the physical parameters of this star. 1. Introduction The evolved star Canopus (α Carinae, HD45348) is a F0 supergiant (F0Ib) star, the second brightest star (V = 0.72) in the night sky, just after Sirius. During their evolution, intermediate− mass stars like Canopus (M 10 M ) leave the red giant branch (RGB) and enter the blue-giant region, significantly≃ ⊙ increasing their effective temperature and performing the so-called blue loop.
    [Show full text]