Tailoring Electrode/Molecule Interfaces for Organic Electronics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Flash Yellow Powered by the Nationwide Sprint 4G LTE Network Table of Contents
How to Build a Successful Business with Flash Yellow powered by the Nationwide Sprint 4G LTE Network Table of Contents This playbook contains everything you need build a successful business with Flash Wireless! 1. Understand your customer’s needs. GO TO PAGE 3 2. Recommend Flash Yellow in strong service areas. GO TO PAGE 4 a. Strong service map GO TO PAGE 5 3. Help your customer decide on a service plan GO TO PAGE 6 4. Ensure your customer is on the right device GO TO PAGE 8 a. If they are buying a new device GO TO PAGE 9 b. If they are bringing their own device GO TO PAGE 15 5. Device Appendix – Is your customer’s device compatible? GO TO PAGE 28 2 Step 1. Understand your customer’s needs • Mostly voice and text - Flash Yellow network would be a good fit in most metropolitan areas. For suburban / rural areas, check to see if they live in a strong Flash Yellow service area. • Average to heavy data user - Check to see if they live in a strong Flash Yellow service area. See page 5. If not, guide them to Flash Green or Flash Purple network to ensure they get the best customer experience. Remember, a good customer experience is the key to keeping a long-term customer! 3 Step 2. Recommend Flash Yellow in strong areas • Review Flash Yellow’s strong service areas. Focus your Flash Yellow customer acquisition efforts on these areas to ensure high customer satisfaction and retention. See page 5. o This is a top 24 list, the network is strong in other areas too. -

Select Smartphones and Tablets with Qualcomm® Quick Charge™ 2.0 Technology
Select smartphones and tablets with Qualcomm® Quick Charge™ 2.0 technology + Asus Transformer T100 + Samsung Galaxy S6 + Asus Zenfone 2 + Samsung Galaxy S6 Edge + Droid Turbo by Motorola + Samsung Note 4 + Fujitsu Arrows NX + Samsung Note Edge + Fujitsu F-02G + Sharp Aquos Pad + Fujitsu F-03G + Sharp Aquos Zeta + Fujitsu F-05F + Sharp SH01G/02G + Google Nexus 6 + Sony Xperia Z2 (Japan) + HTC Butterfly 2 + Sony Xperia Z2 Tablet (Japan) + HTC One (M8) + Sony Xperia Z3 + HTC One (M9) + Sony Xperia Z3 Tablet + Kyocera Urbano L03 + Sony Xperia Z4 + LeTV One Max + Sony Xperia Z4 Tablet + LeTV One Pro + Xiaomi Mi 3 + LG G Flex 2 + Xiaomi Mi 4 + LG G4 + Xiaomi Mi Note + New Moto X by Motorola + Xiaomi Mi Note Pro + Panasonic CM-1 + Yota Phone 2 + Samsung Galaxy S5 (Japan) These devices contain the hardware necessary to achieve Quick Charge 2.0. It is at the device manufacturer’s discretion to fully enable this feature. A Quick Charge 2.0 certified power adapter is required. Different Quick Charge 2.0 implementations may result in different charging times. www.qualcomm.com/quickcharge Qualcomm Quick Charge is a product of Qualcom Technologies, Inc. Updated 6/2015 Certified Accessories + Air-J Multi Voltage AC Charger + Motorola TurboPower 15 Wall Charger + APE Technology AC/DC Adapter + Naztech N210 Travel Charger + APE Technology Car Charger + Naztech Phantom Vehicle Charger + APE Technology Power Bank + NTT DOCOMO AC Adapter + Aukey PA-U28 Turbo USB Universal Wall Charger + Power Partners AC Adapter + CellTrend Car Charger + Powermod Car Charger -
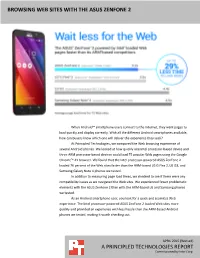
Browsing Web Sites with the Asus Zenfone 2
BROWSING WEB SITES WITH THE ASUS ZENFONE 2 When Android™ smartphone users connect to the Internet, they want pages to load quickly and display correctly. With all the different Android smartphones available, how can buyers know which one will deliver the experience they seek? At Principled Technologies, we compared the Web browsing experience of several Android phones. We looked at how quickly one Intel processor-based device and three ARM processor-based devices could load 75 popular Web pages using the Google Chrome™ 41 browser. We found that the Intel processor-powered ASUS ZenFone 2 loaded 76 percent of the Web sites faster than the ARM-based LG G Flex 2, LG G3, and Samsung Galaxy Note 4 phones we tested. In addition to measuring page load times, we checked to see if there were any compatibility issues as we navigated the Web sites. We experienced fewer problematic elements with the ASUS ZenFone 2 than with the ARM-based LG and Samsung phones we tested. As an Android smartphone user, you look for a quick and seamless Web experience. The Intel processor-powered ASUS ZenFone 2 loaded Web sites more quickly and provided an experience with less hassle than the ARM-based Android phones we tested, making it worth checking out. APRIL 2015 (Revised) A PRINCIPLED TECHNOLOGIES REPORT Commissioned by Intel Corp. A BETTER ANDROID WEB EXPERIENCE WITH ASUS & INTEL Android smartphones are a great way to view Web sites, though they don’t all behave the same way. A mobile device that does a speedy job of loading pages while displaying elements correctly can really improve the user experience. -
Barometer of Mobile Internet Connections in Switzerland
Barometer of mobile internet connections in Switzerland Publication of March 06th 2020 2019 report nPerf is a trademark owned by nPerf SAS, 87 rue de Sèze 69006 LYON – France. Contents 1 Summary of overall results .......................................................................................................... 2 1.1 nPerf score, all technologies combined, [2G->4G] ............................................................... 2 1.2 Our analysis ........................................................................................................................... 3 2 Overall results ............................................................................................................................... 3 2.1 Data amount and distribution ............................................................................................... 3 2.2 Success rate [2G->4G] ........................................................................................................... 4 2.3 Download speed [2G->4G] ..................................................................................................... 4 2.4 Upload speed [2G->4G] ......................................................................................................... 4 2.5 Latency [2G->4G] ................................................................................................................... 5 2.6 Browsing test [2G->4G] ......................................................................................................... 5 2.7 Streaming test [2G->4G] -

Barometer of Mobile Internet Connections in Indonesia Publication of March 14Th 2018
Barometer of mobile Internet connections in Indonesia Publication of March 14th 2018 Year 2017 nPerf is a trademark owned by nPerf SAS, 87 rue de Sèze 69006 LYON – France. Contents 1 Methodology ................................................................................................................................. 2 1.1 The panel ............................................................................................................................... 2 1.2 Speed and latency tests ....................................................................................................... 2 1.2.1 Objectives and operation of the speed and latency tests ............................................ 2 1.2.2 nPerf servers .................................................................................................................. 2 1.3 Tests Quality of Service (QoS) .............................................................................................. 2 1.3.1 The browsing test .......................................................................................................... 2 1.3.2 YouTube streaming test ................................................................................................ 3 1.4 Filtering of test results .......................................................................................................... 3 1.4.1 Filtering of devices ........................................................................................................ 3 2 Overall results 2G/3G/4G ............................................................................................................ -

중국의 신생 스마트폰 기업들이 위협적인 이유 배은준 책임연구원 [email protected] 홍일선 책임연구원 [email protected]
LGERI 리포트 중국의 신생 스마트폰 기업들이 위협적인 이유 배은준 책임연구원 [email protected] 홍일선 책임연구원 [email protected] Ⅰ. 중국 기업, 스마트폰 시장을 흔들다 Ⅱ. 중국 2세대 스마트폰 기업들의 성장 전략, 세그멘테이션 Ⅲ. 2세대 기업이 주목한 중국 스마트폰 시장의 특징 Ⅳ. 세그멘테이션 경쟁의 확산 가능성 화웨이, ZTE, 레노보, 쿨패드 등 중국의 1세대 스마트폰 기업들이 글로벌 규모로 성장하면서 스마트폰 시장 의 경쟁구도는 급변했다. 하지만 중국 시장이 가져오는 위협은 이것으로 끝나지 않을 전망이다. 중국 시장에서 는 이미 1세대 기업에 이어 새로운 2세대 기업이 빠르게 성장하고 있다. 세계 최대 스마트폰 시장으로 자리매김 한 중국은 어제의 중소기업을 오늘의 글로벌 기업으로 길러내는 인큐베이터가 되고 있다. 샤오미는 불과 4년만 에 글로벌 기업들과 어깨를 나란히 하고 있고, 오포, 비보 등 새로운 기업들이 중국으로부터 신흥시장으로 뻗어 나가고 있다. 이들 세 개 기업이 작년 중국에서 판매한 스마트폰은 모두 3,900만대, 한국 시장의 1.6배에 이른 다. 이들 2세대 기업의 성장이 가져올 스마트폰의 시장의 변화는 예상하기 어려울 정도이다. 이들 중국 2세대 스마트폰 기업들은 ① 세계 최대 시장을 기반으로 유래 없이 빠른 속도로 성장하고 있고, ② 글로벌 기업과의 경쟁, 그리고 수 없이 많은 중소 기업과의 경쟁에서 생존하고, 성장하는 전략을 터득했다. ③ 게다가 이들은 향후 스마트폰 시장의 성장을 주도할 신흥 시장 소비자에 대한 이해가 높다. 우리가 중국 2세 대 기업을 반짝 스타로 간과할 수 없는 이유이다. 특히, 2세대 기업의 세그멘테이션 전략에 주목할 필요가 있다. 샤오미, 오포, 비보와 같은 기업들은 글로벌 기업의 제품을 모방하는 데 급급한 다른 중국 기업들과는 달리, 카메라, 오디오, 여성, 젊은이 등으로 시장을 세분화하고, 목표 고객을 명확히 하는 전략을 전개하고 있다. ▶ 셀카 사용자의 증가에 맞춰 전면에 고화소 카메라를 탑재한 모델, ▶ 음 질을 중시하는 중국 소비자 특성에 타게팅하여 고품질 오디오 부품을 채용한 모델, ▶ 매년 두 배 가까이 성장하는 여 성 스마트폰 사용자에 초점을 맞춰 스타일리쉬 디자인과 다양한 색상을 입힌 모델로 소비자들에게 다가가고 있고, ▶ 현재 스마트폰 시장의 주력 소비자인 젊은이들에 초점을 맞춰 온라인 마케팅, 유통을 전개하고 있다. -

Electronic 3D Models Catalogue (On July 26, 2019)
Electronic 3D models Catalogue (on July 26, 2019) Acer 001 Acer Iconia Tab A510 002 Acer Liquid Z5 003 Acer Liquid S2 Red 004 Acer Liquid S2 Black 005 Acer Iconia Tab A3 White 006 Acer Iconia Tab A1-810 White 007 Acer Iconia W4 008 Acer Liquid E3 Black 009 Acer Liquid E3 Silver 010 Acer Iconia B1-720 Iron Gray 011 Acer Iconia B1-720 Red 012 Acer Iconia B1-720 White 013 Acer Liquid Z3 Rock Black 014 Acer Liquid Z3 Classic White 015 Acer Iconia One 7 B1-730 Black 016 Acer Iconia One 7 B1-730 Red 017 Acer Iconia One 7 B1-730 Yellow 018 Acer Iconia One 7 B1-730 Green 019 Acer Iconia One 7 B1-730 Pink 020 Acer Iconia One 7 B1-730 Orange 021 Acer Iconia One 7 B1-730 Purple 022 Acer Iconia One 7 B1-730 White 023 Acer Iconia One 7 B1-730 Blue 024 Acer Iconia One 7 B1-730 Cyan 025 Acer Aspire Switch 10 026 Acer Iconia Tab A1-810 Red 027 Acer Iconia Tab A1-810 Black 028 Acer Iconia A1-830 White 029 Acer Liquid Z4 White 030 Acer Liquid Z4 Black 031 Acer Liquid Z200 Essential White 032 Acer Liquid Z200 Titanium Black 033 Acer Liquid Z200 Fragrant Pink 034 Acer Liquid Z200 Sky Blue 035 Acer Liquid Z200 Sunshine Yellow 036 Acer Liquid Jade Black 037 Acer Liquid Jade Green 038 Acer Liquid Jade White 039 Acer Liquid Z500 Sandy Silver 040 Acer Liquid Z500 Aquamarine Green 041 Acer Liquid Z500 Titanium Black 042 Acer Iconia Tab 7 (A1-713) 043 Acer Iconia Tab 7 (A1-713HD) 044 Acer Liquid E700 Burgundy Red 045 Acer Liquid E700 Titan Black 046 Acer Iconia Tab 8 047 Acer Liquid X1 Graphite Black 048 Acer Liquid X1 Wine Red 049 Acer Iconia Tab 8 W 050 Acer -
The Shape of Innovation. with LG, It’S All Possible.™ Perfect for the Palm of Your Hand; Made to Match the Contour of Your Face
The shape of innovation. With LG, it’s all possible.™ Perfect for the palm of your hand; made to match the contour of your face. Curved is the natural shape of the world around you, and now it is redefining the shape of the smartphone. The LG G Flex is innovation for the next generation, providing an ergonomic design and the most immersive viewing experience that is—quite literally—designed around you. LG G Flex… the world’s first curved, flexible smartphone. Perfect for the palm of your hand; made to match the contour of your face. Curved is the natural shape of the world around you, and now it is redefining the shape of the smartphone. The LG G Flex is innovation for the next generation, providing an ergonomic design and the most immersive viewing experience that is—quite literally—designed around you. LG G Flex… the world’s first curved, flexible smartphone. FLUID LOCK SCREEN The lock screen strikes a balance between art and function, showing wallpaper that changes depending on the time of day or how the LG G Flex is held. And, the display has unique visual unlock Innovative effects with contextual sounds. Curved Design KNOCKON Wake the display with two simple taps. COMFORTABLE FORM FACTOR Put it to sleep by double tapping on an empty area of the screen or the task bar. The world’s first curved, flexible smartphone provides the ultimate DUAL WINDOW ease of use, ideal for two-handed Divide the expansive 6.0" screen typing and one-handed scrolling.* INTUITIVE REAR KEY into separate windows, giving a *The flexibility of this product is limited. -

HR Kompatibilitätsübersicht
HR-imotion Kompatibilität/Compatibility 2018 / 11 Gerätetyp Telefon 22410001 23010201 22110001 23010001 23010101 22010401 22010501 22010301 22010201 22110101 22010701 22011101 22010101 22210101 22210001 23510101 23010501 23010601 23010701 23510320 22610001 23510420 Smartphone Acer Liquid Zest Plus Smartphone AEG Voxtel M250 Smartphone Alcatel 1X Smartphone Alcatel 3 Smartphone Alcatel 3C Smartphone Alcatel 3V Smartphone Alcatel 3X Smartphone Alcatel 5 Smartphone Alcatel 5v Smartphone Alcatel 7 Smartphone Alcatel A3 Smartphone Alcatel A3 XL Smartphone Alcatel A5 LED Smartphone Alcatel Idol 4S Smartphone Alcatel U5 Smartphone Allview P8 Pro Smartphone Allview Soul X5 Pro Smartphone Allview V3 Viper Smartphone Allview X3 Soul Smartphone Allview X5 Soul Smartphone Apple iPhone Smartphone Apple iPhone 3G / 3GS Smartphone Apple iPhone 4 / 4S Smartphone Apple iPhone 5 / 5S Smartphone Apple iPhone 5C Smartphone Apple iPhone 6 / 6S Smartphone Apple iPhone 6 Plus / 6S Plus Smartphone Apple iPhone 7 Smartphone Apple iPhone 7 Plus Smartphone Apple iPhone 8 Smartphone Apple iPhone 8 Plus Smartphone Apple iPhone SE Smartphone Apple iPhone X Smartphone Apple iPhone XR Smartphone Apple iPhone Xs Smartphone Apple iPhone Xs Max Smartphone Archos 50 Saphir Smartphone Archos Diamond 2 Plus Smartphone Archos Saphir 50x Smartphone Asus ROG Phone Smartphone Asus ZenFone 3 Smartphone Asus ZenFone 3 Deluxe Smartphone Asus ZenFone 3 Zoom Smartphone Asus Zenfone 5 Lite ZC600KL Smartphone Asus Zenfone 5 ZE620KL Smartphone Asus Zenfone 5z ZS620KL Smartphone Asus -

Udynamo Compatibility List
uDynamo Compatibility List Reader Manuf. Device Name Alt. Model Info Model Info OS OS Version Carrier Date Added Date Tested Type iDynamo 5 Apple iPad Air 2 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad Air* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad with Retina Display* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini 3 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini 2 Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPad mini* Lightning N/A iOS N/A N/A Tablet iDynamo 5 Apple iPhone 5c* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 5s* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 5* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPod touch (5th* generation) Lightning N/A iOS N/A N/A iPod iDynamo 5 Apple iPhone 6* Lightning N/A iOS N/A N/A Phone iDynamo 5 Apple iPhone 6 Plus* Lightning N/A iOS N/A N/A Phone iDynamo Apple iPad (3rd generation) 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPad 2 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPad 30 PIN N/A iOS N/A N/A Tablet iDynamo Apple iPhone 4s 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPhone 4 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPhone 3GS 30 PIN N/A iOS N/A N/A Phone iDynamo Apple iPod touch (3rd and 4th generation) 30 PIN N/A iOS N/A N/A iPod uDynamo Acer liquid MT liquid MT Android 2.3.6 101.18 1/24/14 1/24/14 uDynamo Alcatel Alcatel OneTouch Fierce 7024W Android 4.2.2 101.18 3/6/14 3/6/14 uDynamo ALCATEL Megane ALCATEL ONE TOUCH 5020T Android 4.1.2 101.18 8/10/15 8/10/15 uDynamo ALCATEL ALCATEL ONE TOUCH IDOL X ALCATEL -

Phone Compatibility
Phone Compatibility • Compatible with iPhone models 4S and above using iOS versions 7 or higher. Last Updated: February 14, 2017 • Compatible with phone models using Android versions 4.1 (Jelly Bean) or higher, and that have the following four sensors: Accelerometer, Gyroscope, Magnetometer, GPS/Location Services. • Phone compatibility information is provided by phone manufacturers and third-party sources. While every attempt is made to ensure the accuracy of this information, this list should only be used as a guide. As phones are consistently introduced to market, this list may not be all inclusive and will be updated as new information is received. Please check your phone for the required sensors and operating system. Brand Phone Compatible Non-Compatible Acer Acer Iconia Talk S • Acer Acer Jade Primo • Acer Acer Liquid E3 • Acer Acer Liquid E600 • Acer Acer Liquid E700 • Acer Acer Liquid Jade • Acer Acer Liquid Jade 2 • Acer Acer Liquid Jade Primo • Acer Acer Liquid Jade S • Acer Acer Liquid Jade Z • Acer Acer Liquid M220 • Acer Acer Liquid S1 • Acer Acer Liquid S2 • Acer Acer Liquid X1 • Acer Acer Liquid X2 • Acer Acer Liquid Z200 • Acer Acer Liquid Z220 • Acer Acer Liquid Z3 • Acer Acer Liquid Z4 • Acer Acer Liquid Z410 • Acer Acer Liquid Z5 • Acer Acer Liquid Z500 • Acer Acer Liquid Z520 • Acer Acer Liquid Z6 • Acer Acer Liquid Z6 Plus • Acer Acer Liquid Zest • Acer Acer Liquid Zest Plus • Acer Acer Predator 8 • Alcatel Alcatel Fierce • Alcatel Alcatel Fierce 4 • Alcatel Alcatel Flash Plus 2 • Alcatel Alcatel Go Play • Alcatel Alcatel Idol 4 • Alcatel Alcatel Idol 4s • Alcatel Alcatel One Touch Fire C • Alcatel Alcatel One Touch Fire E • Alcatel Alcatel One Touch Fire S • 1 Phone Compatibility • Compatible with iPhone models 4S and above using iOS versions 7 or higher. -

HR Kompatibilitätsübersicht
Kompatibilitätsübersicht HR-imotion HR-imotion Kompatibilität/Compatibility 2017 / 03 Gerätetyp Telefon 22410001 23010201 22110001 23010001 23010101 22010401 22010501 22010301 22010201 22110101 22010701 22011101 22010101 22210101 22210001 23510101 23010501 23010601 23010701 23510320 22610001 23510420 Smartphone Acer Liquid Zest Plus Smartphone AEG Voxtel M250 Smartphone Alcatel A3 Smartphone Alcatel A3 XL Smartphone Alcatel A5 LED Smartphone Alcatel Idol 4S Smartphone Alcatel U5 Smartphone Allview X3 Soul Smartphone Apple iPhone Smartphone Apple iPhone 3G / 3GS Smartphone Apple iPhone 4 / 4S Smartphone Apple iPhone 5 / 5S Smartphone Apple iPhone 5C Smartphone Apple iPhone 6 / 6S Smartphone Apple iPhone 6 Plus / 6S Plus Smartphone Apple iPhone 7 Smartphone Apple iPhone 7 Plus Smartphone Apple iPhone SE Smartphone Archos 50 Saphir Smartphone Archos Diamond 2 Plus Smartphone Asus ZenFone 3 Smartphone Asus ZenFone 3 Deluxe Smartphone Asus ZenFone 3 Zoom Smartphone Asus ZenFone AR Smartphone BlackBerry Classic Smartphone Blackberry DTEK 50 Smartphone Blackberry KEYOne Smartphone BlackBerry Passport Smartphone BlackBerry Priv Smartphone BlackBerry Z30 Smartphone BQ Aquaris X5 Smartphone BQ Aquaris X5 Plus Smartphone CAT B15 Smartphone Cubot P11 Smartphone Cubot S500 Smartphone Elephone P8000 Smartphone Emporia Pure Smartphone Gigaset GS160 Smartphone Gigaset ME Smartphone Gigaset ME Pro Smartphone Gigaset ME Pure Smartphone Google Nexus 5 Smartphone Google Nexus 5X Smartphone Google Nexus 6 Smartphone Google Nexus 6P Smartphone Google Pixel