An Examination of the Swiss Banking Sector∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Die Kantonalbanken in Zahlen
Kennziffern und Adressen Die Kantonalbanken der Kantonalbanken in Zahlen Kennzahlen der 24 Kantonalbanken Eckdaten der 24 Kantonalbanken Angaben per 31.12.2018 (inkl. Tochtergesellschaften) Angaben per 31.12.2018 Kantonalbank Gründungsjahr Bilanzsumme Geschäftsstellen Personalbestand Kantonalbank Rechts- Dotations-/ PS-Kapital Kotierung Staats- in Mio. CHF teilzeitbereinigt form Aktienkapital in Mio. CHF SIX garantie in Mio. CHF Aargauische Kantonalbank 1913 28‘351 31 708 Aargauische Kantonalbank örK 200 - - ja Appenzeller Kantonalbank 1899 3‘365 4 81 Appenzeller Kantonalbank örK 30 - - ja Banca dello Stato del Cantone Ticino 1915 14‘322 21 444 Banca dello Stato del Cantone Ticino örK 430 - - ja Banque Cantonale de Fribourg 1892 22‘927 27 382 Banque Cantonale de Fribourg örK 70 - - ja Banque Cantonale de Genève 1816 23‘034 28 761 Banque Cantonale de Genève AG 360 - ja nein Banque Cantonale du Jura 1979 3‘152 12 122 Banque Cantonale du Jura AG 42 - ja ja Banque Cantonale du Valais 1917 16‘122 45 471 Banque Cantonale du Valais AG 158 - ja ja Banque Cantonale Neuchâteloise 1883 10‘847 12 285 Banque Cantonale Neuchâteloise örK 100 - - ja Banque Cantonale Vaudoise 1845 47‘863 72 1‘896 Banque Cantonale Vaudoise AG 86 - ja nein Basellandschaftliche Kantonalbank 1864 25‘341 22 689 Basellandschaftliche Kantonalbank örK 160 57 ja ja Basler Kantonalbank 1899 44‘031 46 1‘238 Basler Kantonalbank örK 304 50 ja ja Berner Kantonalbank 1834 30‘589 60 1‘000 Berner Kantonalbank AG 186 - ja nein Glarner Kantonalbank 1884 5‘982 6 191 Glarner Kantonalbank AG -

A Primer on DOJ's Swiss Bank Program
1012 Broad Street, 2nd Fl Bloomfield, NJ 07003 Tel (973) 783-7000 Fax (973) 338-3955 www.DeBlisLaw.com HIGH-STAKES TAX DEFENSE & COMPLEX CRIMINAL DEFENSE A Primer on DOJ’s Swiss Bank Program a. Background Information From the outside looking in, it is easy to accuse those who are unfamiliar with the Department of Justice’s Swiss Bank Program as living under a rock. But that is presumptuous when you are a tax attorney who is immersed in this work every day. Let’s begin with some background information. The Swiss Bank Program was unveiled on August 29, 2013. It provides a path for Swiss banks to resolve potential criminal liabilities in the United States. In order to participate, Swiss banks had to take the “bull by its horns” and notify the Department of Justice by December 31, 2013 that they had reason to believe that they had committed tax-related criminal crimes in connection with unreported U.S.-related accounts. In other words, they had to “eat crow.” Banks already under criminal investigation for shady banking activities (along with any individuals who work for such banks) were deemed ineligible from participating in the program. In order to be eligible for a non-prosecution agreement, banks must do the following: (1) Make a complete disclosure of their cross-border activities; (2) Provide detailed information on an account-by-account basis for accounts in which U.S. taxpayers have a direct or indirect interest; (3) Cooperate in treaty requests for account information; (4) Provide detailed information as to other banks that transferred funds into secret accounts or that accepted funds when secret accounts were closed; (5) Agree to close accounts of accountholders who fail to come into compliance with U.S. -
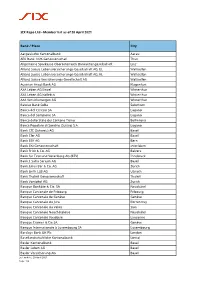
SIX Repo Ltd - Member List As of 20 April 2021
SIX Repo Ltd - Member list as of 20 April 2021 Bank / Place City Aargauische Kantonalbank Aarau AEK Bank 1826 Genossenschaft Thun Allgemeine Sparkasse Oberösterreich Bankaktiengesellschaft Linz Allianz Suisse Lebensversicherungs-Gesellschaft AG, EL Wallisellen Allianz Suisse Lebensversicherungs-Gesellschaft AG, KL Wallisellen Allianz Suisse Versicherungs-Gesellschaft AG Wallisellen Austrian Anadi Bank AG Klagenfurt AXA Leben AG Einzel Winterthur AXA Leben AG Kollektiv Winterthur AXA Versicherungen AG Winterthur Baloise Bank SoBa Solothurn Banca del Ceresio SA Lugano Banca del Sempione SA Lugano Banca dello Stato del Cantone Ticino Bellinzona Banca Popolare di Sondrio (Suisse) S.A. Lugano Bank CIC (Schweiz) AG Basel Bank Cler AG Basel Bank EEK AG Bern Bank EKI Genossenschaft Interlaken Bank Frick & Co. AG Balzers Bank für Tirol und Vorarlberg AG (BTV) Innsbruck Bank J. Safra Sarasin AG Basel Bank Julius Bär & Co. AG Zürich Bank Linth LLB AG Uznach Bank Thalwil Genossenschaft Thalwil Bank Vontobel AG Zürich Banque Bonhôte & Cie. SA Neuchâtel Banque Cantonale de Fribourg Fribourg Banque Cantonale de Genève Genève Banque Cantonale du Jura Porrentruy Banque Cantonale du Valais Sion Banque Cantonale Neuchâteloise Neuchâtel Banque Cantonale Vaudoise Lausanne Banque Cramer & Cie SA Genève Banque Internationale à Luxembourg SA Luxembourg Barclays Bank UK Plc London Basellandschaftliche Kantonalbank Liestal Basler Kantonalbank Basel Basler Leben AG Basel Basler Versicherung AG Basel Last update: 20 April 2021 Page: 1/4 BBVA SA Zürich Bendura Bank -

The Swiss Banking Websites Index Q3 2010/701
indexThe Swiss Banking Websites Index Q3 2010/701 To compile this survey we reviewed over 250 websites, using the Sitemorse automated website optimisation software (page content, templates and infrastructure) to test and rank each website. This report presents a summary of the findings and is produced in association with Supertext. www.supertext.ch We run more tests, in more depth, more often than anyone else. Our results are more accurate, more accessible and more useful than anyone else’s, and our reports are published in more places, read by more people and trusted by more organisations The Swiss Banking Websites Index Q3 2010/701 than anyone else’s. index Contents Welcome note 3 The better you tell, the better you sell 4 The top fifty 5 Time to wait 6 Fatwire - Content Integration Platform™ 7 Most improved site 8 Who’s up and who’s down 8 The bottom twenty 8 Web accessibility denied 9 92% of sites need to consider the impact 10 Welcome to the 8th issue of the Swiss Banking Websites Index. This quarterly survey provides an independent benchmark of over 250 websites, employing more than 600 tests on each page tested. The banking industry needs to improve online quality, compliance and user experience – preferably at the point of website delivery, not as an afterthought. A positive user experience is not simply a matter of beautiful design: the primary requirement is for the website to function properly and quickly. The Sitemorse tests routinely uncover all kinds of problems that can have a big impact on a visitor’s impression – such as dead links, compliance issues, non-functioning email addresses, slow pages, poor ranking in search engines, etc. -

No. 18-12751 Non-Argument Calendar ______
Case: 18-12751 Date Filed: 12/10/2018 Page: 1 of 5 [DO NOT PUBLISH] IN THE UNITED STATES COURT OF APPEALS FOR THE ELEVENTH CIRCUIT ________________________ No. 18-12751 Non-Argument Calendar ________________________ D.C. Docket No. 0:17-cv-62542-BB GIULIANO STEFANO GIOVANNI WILDHABER, Plaintiff-Appellant, versus EFV, EBK-EIDGENOSSISCHE BANKENKOMMISSION (FINMA), ZKB BANK, CREDIT SUISSE AG, AARGAUISCHE KANTONALBANK, APPENZELLER KANTONALBANK, et al., Defendants-Appellees. ________________________ Appeal from the United States District Court for the Southern District of Florida ________________________ (December 10, 2018) Case: 18-12751 Date Filed: 12/10/2018 Page: 2 of 5 Before ED CARNES, Chief Judge, WILSON, and HULL, Circuit Judges. PER CURIAM: Giuliano Wildhaber, a Swiss citizen proceeding pro se, appeals the district court’s order granting the Swiss government’s and twenty-six Swiss banks’ motions to dismiss his complaint, which he filed under the Alien Tort Statute. I. For present purposes we draw the facts from the complaint, accepting them as true and viewing them in the light most favorable to Wildhaber. Butler v. Sheriff of Palm Beach Cty., 685 F.3d 1261, 1263 n.2 (11th Cir. 2012). In December 1988 a referendum was held in Switzerland involving a proposal to restrict land speculation. Although seventy percent of Swiss voters rejected the proposal, in October 1989 the Swiss Federal Council adopted a decree discouraging land speculation by prohibiting the sale of real property within five years of its purchase. The decree caused Wildhaber and other Swiss property owners to suffer economic losses because their property decreased in value. In November 2017 Wildhaber brought claims under the Alien Tort Statute (ATS) against two financial entities of the Swiss government and twenty-six Swiss banks for helping enact, or profiting from, the decree.1 Those claims included, 1 For ease of reference, we will collectively refer to these twenty-eight entities as the defendants unless context makes it necessary to refer to them individually. -

Notice N19 2019
Swiss Instruments to be delisted from CLXNz CH0011115703 Crealogix Holding AG LEHNz CH0022427626 LEM Holding SA SFZNz CH0014284498 Siegfried Holding AG UBS MTF effective 1 July CMBNz CH0225173167 Cembra Money Bank AG LEONz CH0190891181 Leonteq AG SGKNz CH0011484067 St Galler Kantonalbank AG CONz CH0244017502 Conzzeta AG LHNz CH0012214059 LafargeHolcim Ltd SGSNz CH0002497458 SGS SA COTNz CH0360826991 Comet Holding AG LINNz CH0001307757 Bank Linth LLB AG SIGNz CH0435377954 SIG Combibloc Group AG Symbol ISIN Issuer CPENz CH0048854746 Castle Private Equity Ltd LISNz CH0010570759 Chocoladefabriken Lindt & Spruengli AG SIKAz CH0418792922 Sika AG ABBNz CH0012221716 ABB Ltd CPHNz CH0001624714 CPH Chemie & Papier Holding AG LISPz CH0010570767 Chocoladefabriken Lindt & Spruengli AG SIMAz CH0014420878 UBS CH Property Fund - Swiss Mixed Sima ADENz CH0012138605 Adecco Group AG CSGNz CH0012138530 Credit Suisse Group AG LLQz CH0033813293 Lalique Group SA SLHNz CH0014852781 Swiss Life Holding AG ADVNz CH0008967926 Adval Tech Holding AG DAEz CH0030486770 Daetwyler Holding AG LOGNz CH0025751329 Logitech International SA SNBNz CH0001319265 Schweizerische Nationalbank ADXNz CH0029850754 Addex Therapeutics Ltd DCNz CH0008531045 Datacolor AG LONNz CH0013841017 Lonza Group AG SOONz CH0012549785 Sonova Holding AG AEVSz CH0478634105 AEVIS VICTORIA SA DESNz CH0020739006 Dottikon Es Holding AG LUKNz CH0011693600 Luzerner Kantonalbank AG SPCEz CH0009153310 Spice Private Equity AG AIREz CH0010947627 Airesis SA DKSHz CH0126673539 DKSH Holding AG MBTNz CH0108503795 -

Notice N19 2019
UBS MTF Market Notice Swiss Market Removal 28 June 2019 Dear Member, Following the announcement of the Swiss Federal Department of Finance on June 24 (FDF prepared to activate measure to protect Swiss stock exchange infrastructure), and further to our notice of the same date, UBS MTF will remove all instruments issued by companies with registered offices in Switzerland which are listed on Swiss trading venues. This update will take effect from 1 July. Our daily Stock Universe file, published on our website at https://www.ubs.com/global/en/investment- bank/ib/multilateral-trading-facility/reference-data.html and by SFTP, will reflect the removal of these instruments as of this date. Instruments not subject to the Swiss measure are unaffected; a list of affected instruments is attached to this notice. If you have any queries regarding this notice please contact the UBS MTF Supervisors at +44 207 568 2052 or [email protected]. UBS MTF Management Notice N19 2019 UBS MTF Notices and documentation are available at https://www.ubs.com/mtf. If you have any queries regarding this notice, or comments on the above, please contact the UBS MTF Supervisors at +44 20 7568 2052 or [email protected]. UBS MTF is operated by UBS AGLB which is authorised by the Prudential Regulation Authority and regulated by the UK Financial Conduct Authority and Prudential Regulation Authority. UBS AG is a public company incorporated with limited liability in Switzerland domiciled in the Canton of Basel-City and the Canton of Zurich respectively registered at the Commercial Registry offices in those Cantons with Identification No: CHE-101.329.561 as from 18 December 2013 (and prior to 18 December 2013 with Identification No: CH-270.3.004.646-4) and having respective head offices at Aeschenvorstadt 1, 4051 Basel and Bahnhofstrasse 45, 8001 Zurich, Switzerland and is authorised and regulated by the Financial Market Supervisory Authority in Switzerland. -

Die Kantonalbanken in Zahlen
1000D / Adressen der Kantonalbanken ©VSKB 05.11 Aargauische Kantonalbank Banque Cantonale du Valais Glarner Kantonalbank Schwyzer Kantonalbank Bahnhofplatz 1, Postfach Place des Cèdres 8 Hauptstrasse 21 Bahnhofstrasse 3, Postfach 263 5001 Aarau 1951 Sion 8750 Glarus 6431 Schw yz Tel. 062 835 77 77 Tel. 0848 952 952 Tel. 0844 773 773 Tel. 058 800 20 20 Fax 062 835 77 78 Fax 027 324 66 66 Fax 055 646 71 55 Fax 058 800 20 21 [email protected] [email protected] [email protected] [email protected] www.akb.ch www.bcvs.ch www.glkb.ch www.szkb.ch Appenzeller Kantonalbank Banque Cantonale Graubündner Kantonalbank St. Galler Kantonalbank Bankgasse 2 Neuchâteloise Postplatz St. Leonhardstrasse 25 Postfach Place Pury 4 Postfach 9001 St. Gallen 9050 Appenzell 2001 Neuchâtel 7002 Chur Tel. 071 231 31 31 Tel. 071 788 88 88 Tel. 032 723 61 11 Tel. 081 256 96 01 Fax 071 231 32 32 Fax 071 788 88 89 Fax 032 723 62 36 Fax 081 256 99 42 [email protected] Kennziffern und Adressen Die Kantonalbanken [email protected] [email protected] [email protected] www.sgkb.ch www.appkb.ch www.bcn.ch www.gkb.ch der Kantonal banken und ihrer in Zahlen Netzwerkpartner Banca dello Stato del Banque Cantonale Vaudoise Luzerner Kantonalbank Thurgauer Kantonalbank Cantone Ticino Case postale 300 Pilatusstrasse 12 Bankplatz 1 Viale H. Guisan 5 1001 Lausanne Postfach Postfach 160 Casella postale 2027 Tel. 0844 228 228 6002 Luzern 8570 Weinfelden 6501 Bellinzona Fax 021 212 12 22 Tel. 0844 822 811 Tel. -

2018 Annual Report 2018Annual Report BCV at a Glance
Head Office Place St-François 14 Case postale 300 1001 Lausanne Switzerland Report2018 Annual Phone: +41 21 212 10 10 Swift code: BCVLCH2L 2018 Annual Report Clearing number: 767 GIIN: 6X567Y.00000.LE.756 www.bcv.ch [email protected] BCV at a glance 2018 highlights We delivered very solid results in an operating The Vaud Cantonal Government appointed two new environment where the economic climate was generally members to the Board of Directors favorable but interest rates remained negative • Fabienne Freymond Cantone replaced Luc Recordon • Volumes expanded across all the Bank’s key business on 26 April 2018. sectors, and revenues rose 1% to CHF 977m. • Jean-François Schwarz was named to succeed • Operating profit increased 4% to CHF 403m, driven Paul-André Sanglard as of 1 January 2019. by firm cost control. • Net profit was up 9% to CHF 350m, underpinning We paid out CHF 284m to our shareholders and a recommended CHF 2 increase in the dividend to extended our distribution policy CHF 35. • In May 2018, BCV paid an ordinary dividend of CHF 23 per share and distributed CHF 10 per share out BCV’s credit ratings were reaffirmed by the two main of paid-in reserves, thus returning a total CHF 284m rating agencies to our shareholders. This payout, together with the • Standard and Poor’s reaffirmed our AA rating, and appreciation in our share price, equates to a total Moody’s reaffirmed our Aa2 rating, both with a return of 5.3% in 2018. stable outlook. BCV is one of the best rated banks in • We extended our distribution policy for another five the world without an explicit government guarantee. -

Basel III Pillar 3 Report
Basel III Pillar 3 Report Market discipline Basel III Pillar 3 Report at 31 December 2015 22 April 2016 / Banque Cantonale Vaudoise / Version 2.0 41-501/09.01 Basel III Pillar 3 Report 2 Table of contents 1.1 Disclosure policy ......................................................................................................... 3 1.2 Scope .......................................................................................................................... 3 2. Capital structure ............................................................................................................. 5 3. Capital adequacy ............................................................................................................ 6 4. Risk exposure and assessment ...................................................................................... 9 4.1 Risk-management objectives and governance ......................................................... 10 4.2 Classification of risks and risk-assessment principles ............................................... 11 4.3 Credit risk .................................................................................................................. 12 4.4 Non-counterparty-related assets ............................................................................... 45 4.5 Market risk ................................................................................................................. 46 4.6 Operational risk ........................................................................................................ -

2017 Annual Report 2017Annual Report BCV at a Glance
Head Office Place St-François 14 Case postale 300 1001 Lausanne Switzerland Report2017 Annual Phone: +41 21 212 10 10 Swift code: BCVLCH2L 2017 Annual Report Clearing number: 767 GIIN: 6X567Y.00000.LE.756 www.bcv.ch [email protected] BCV at a glance 2017 highlights We delivered very solid results despite the ongoing We added more new services and features to our digital negative-interest-rate environment banking line-up • Volumes continued to expand, and gross revenues • Customers can now open an account or take out a edged up 1.5%. mortgage loan entirely online. • Operating profit increased 1% to CHF 387m, • We rolled out our BCV TWINT app – a digital driven by firm cost control, lower depreciation and wallet for making in-store and online purchases in amortization, and a decrease in other provisions. Switzerland and transferring money to friends. • Net profit came in at CHF 320m (+3%), consistent with previous years. We paid out CHF 284m to our shareholders • BCV paid an ordinary dividend of CHF 23 per New members were appointed to the Executive Board share and distributed CHF 10 per share out of and Board of Directors paid-in reserves, thus returning a total CHF 284m • The Vaud Cantonal Government appointed Jacques to our shareholders. This payout, together with the de Watteville to succeed Olivier Steimer as the appreciation in our share price, equates to a total Chairman of BCV’s Board of Directors starting on return of 19.1% in 2017. 1 January 2018. • Two new members joined BCV’s Executive Board: We extended our distribution policy for another five Christian Meixenberger as head of the Business years beginning with the 2018 reporting period Support Division and Andreas Diemant as head of • In light of the planned reduction in Vaud Canton’s the Corporate Banking Division. -

Authorised Banks and Securities Firms
Authorised banks and securities firms Name City Licensing Bank type Securities firms type no activity as securities firm non-account-holding securities firms Category Aargauische Kantonalbank Aarau Bank Cantonal banks Swiss securities firm 3 ABANCA CORPORACION BANCARIA S.A., Betanzos, Genève 1 Foreign bank branch office First branch office of a foreign bank X 5 succursale de Genève acrevis Bank AG St. Gallen Bank Regional banks and savings banks Swiss securities firm 4 AEK BANK 1826 Genossenschaft Thun Bank Regional banks and savings banks Swiss securities firm 4 AFS Equity & Derivatives B.V., Amsterdam, Regensdorf Foreign securities firm branch office Securities firm First branch office of a foreign X 5 Zweigniederlassung Regensdorf securities firm Allfunds Bank International S.A., Luxembourg, Zurich Zürich Foreign bank branch office First branch office of a foreign bank First branch office of a foreign 5 Branch securities firm Alpha RHEINTAL Bank AG Heerbrugg Bank Regional banks and savings banks Swiss securities firm 4 Alternative Bank Schweiz AG Olten Bank Other banks Swiss securities firm 4 Appenzeller Kantonalbank Appenzell Bank Cantonal banks Swiss securities firm 4 Aquila AG Zürich Bank Other banks Swiss securities firm 5 Arab Bank (Switzerland) Ltd. Genève 3 Bank Foreign-controlled banks Foreign-controlled securities 4 firm AXION SWISS BANK SA Lugano Bank Banks specialised in exchange, Swiss securities firm 4 securities and asset management business Baader Helvea AG Zürich Securities firm Securities firm Foreign-controlled securities