General Disclaimer One Or More of the Following Statements May Affect
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Planetary Science Institute
PLANETARY SCIENCE INSTITUTE N7'6-3qo84 (NAS A'-CR:1'V7! 3 ) ASTEROIDAL AND PLANETARY ANALYSIS Final Report (Planetary Science Ariz.) 163 p HC $6.75 Inst., Tucson, CSCL 03A Unclas G3/89 15176 i-'' NSA tiFACIWj INP BRANC NASW 2718 ASTEROIDAL AND PLANETARY ANALYSIS Final Report 11 August 1975 Submitted by: Planetary Science Institute 252 W. Ina Road, Suite D Tucson, Arizona 85704 William K. Hartmann Manager TASK 1: ASTEROID SPECTROPHOTOMETRY AND INTERPRETATION (Principal Investigator: Clark R. Chapman) A.* INTRODUCTION The asteroid research program during 1974/5 has three major goals: (1) continued spectrophotometric reconnaissance of the asteroid belt to define compositional types; (2) detailed spectrophotometric observations of particular asteroids, especially to determine variations with rotational phase, if any; and (3) synthesis of these data with other physical studies of asteroids and interpretation of the implications of physical studies of the asteroids for meteoritics and solar system history. The program has been an especially fruitful one, yielding fundamental new insights to the nature of the asteroids and the implications for the early development of the terrestrial planets. In particular, it is believed that the level of understanding of the asteroids has been reached, and sufficiently fundamental questions raised about their nature, that serious consideration should be given to possible future spacecraft missions directed to study a sample of asteroids at close range. Anders (1971) has argued that serious consideration of asteroid missions should be postponed until ground-based techniques for studying asteroids had been sufficiently exploited so that we could intelligently select appropriate asteroids for spacecraft targeting. It is clear that that point has been reached, ,and now that relatively inexpensive fly-by missions have been discovered to be possible by utilizing Venus and Earth gravity assists (Bender and Friedlander, 1975), serious planning for such missions ought to begin. -

Occuthubn(Gnewstetter
Occuthubn(gNewstetter Volume I, Number 3 January, 1975 Edited and Published by X. F, DaBoli at 6 N 106 White Oak Lane, St, Charles, Illinois 60174 U. S. A. GRAZING OCCULTATION TRACKS IN THE 1975 OCCULTATIDNS OF STARS BY (433) EROS 94 Pierce Rd., Watertown, Mass. 02172, OBSERVER'S HANDBOOK phone 6}7, 926-2678 Or 864-7360. In David It Dunham order to catch the event, it will be flue to an unfortunate error at the necessary to have observers at roughly printer's, the maps of the grazing qc- A map showing Brian Marsden's predic- even intervals across the whole region cu1tation tracks for 1975 were not in- tion for the path of the occultation of uncertginty. Observers are there- cluded in the 1975 Obgeme7"8 Hand- of Kappa Geminorum by Eros across fore urged to contact the above to co- book; the maps which appear are actu- southern Quebec, the northern tip of ordinate plans. ally those for 1974. We hope to pub- New Hainpshlre, and southern Maine is lish the correct maps in the February shown on p. 9 of the January issue of flue to the relatively low a?titude and Journal of the Royal Astronomical So- Sky and Telescope. Another prediction brtght moonlight, naked-eye observa- cietjjof Canada, and to send the maps was conputecf recently by Paul Herget tions will not be sufficient; at least to a interested observers. These at the Minor Ptanet Center at Cimin- smait binoculars or opera g7asses maps will be available early in the natl Observatory, According to Herget. -

The Complete the Complete Guide to Guide to Guide to Observing Observing Lunar, Grazing and Lunar, Grazing and Asteroid Occulta
The Complete Guide to Observing Lunar, Grazing and Asteroid Occultations Published by the International Occultation Timing Association Richard Nugent, Editor Copyright 2007 International Occultation Timing Association, Richard Nugent, Editor. All rights reserved. No part of this publication may be reproduced, distributed or copied in any manner without the written permission from the Editor in Chief. No part of this publication may be reproduced, stored in any retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under the 1976 United States Copyright Act and with the written permission of the Editor and Publisher. Request to the Editor should be sent via email: [email protected]. While the Editor, Authors and Publisher have made their best efforts in preparing the IOTA Occultation Manual, they make no representation or warranties with respect to the accuracy and completeness regard to its contents. The Publisher, Editor and Authors specifically disclaim any implied warranties of merchantability or fitness of the material presented herein for any purpose. The advice and strategies contained herein may not be suitable for your situation and the reader and/or user assumes full responsibility for using and attempting the methods and techniques presented. Neither the publisher nor the authors shall be liable for any loss of profit or any damages, including but not limited to special, incidental, consequential, or other damages and any loss or injury. Persons are advised that occultation observations involve substantial risk and are advised to take the necessary precautions before attempting such observations. Editor in Chief: Richard Nugent Assistant Editor: Lydia Lousteaux Contributors: Trudy E. -

Adrian Zielonka's June 2021 Astronomy and Space News
Astronomy News Night Sky 2021 - June Sunrise Sunset Mercury Sets / Venus Sets Rises 1st – 5:02am 1st – 9:17pm 1st – 10:08pm 1st – 10:40pm 10th – 4:57am 10th – 9:25pm 11th – Inf 10th – 10:52pm 20th – 4:56am 20th – 9:29pm Conjunction 20th – 10:57pm 30th – 5:00am 30th – 9:29pm 26th – 4:18am 30th – 10:54pm 30th – 4:05am Moon Rise Moon Set Moon Rise Moon Set 1st - 2:05am 1st - 11:25am 20th – 4:05pm 21st – 2:40am 2nd – 2:26am (ESE) (WSW) 21st – 5:32pm (WSW) 3rd – 2:43am 2nd – 12:40pm (ESE) 22nd – 3:04am 4th – 2:57am 3rd – 1:52pm 22nd – 7:01pm 23rd – 3:34am 5th – 3:11am (E) 4th – 3:01pm (W) 23rd – 8:28pm 24th – 4:15am 6th – 3:25am 5th – 4:09pm 24th – 9:45pm 25th – 5:11am 7th – 3:41am 6th – 5:17pm 25th – 10:47pm 26th – 6:21am (ENE) 7th – 6:26pm 26th – 11:33pm 27th – 7:41am 8th – 3:58 am (WNW) 28th – 12:05am 28th – 9:02am 9th – 4:20am 8th – 7:34pm 29th – 12:29am 29th – 10:21am 10th – 4:48am 9th – 8:42pm (ESE) (WSW) 11th – 5:25am 10th – 9:47pm 30th – 12:48am 30th – 11:36am 12th – 6:11am 11th – 10:46pm 13th – 7:09am 12th – 11:35pm - - - - - - - - - - - - - - 14th – 8:16am 14th – 12:15am 15th – 9:29am 15th – 12:45am All times Moon Phases 16th – 10:44am 16th – 1:10am in notes are set Last Quarter – 2nd (ENE) 17th – 1:30am for New Moon – 10th 17th – 12:02pm (WNW) Somerton First Quarter – 18th – 1:20pm 18th – 1:48am unless stated 18th 19th – 2:41pm (E) 19th – 2:04am (W) Full Moon – 24th 20th – 2:21am A useful site: www.heavens-above.com A S Zielonka From the 30th May – 1st June Mars passes close to the star Kappa Geminorum (3.5 mag). -

Adrian Zielonka's December 2020 Astronomy and Space News
Astronomy News Night Sky 2020 - December Sunrise Sunset Mercury Venus Rises 1st – 7:53am 1st – 4:07pm 1st – 5:19am 10th – 8:04am 10th – 4:04pm Not Visible 10th – 5:46am 20th – 8:12am 20th – 4:06pm this month. 20th – 6:16am 30th – 8:15am 30th – 4:13pm 30th – 6:43am Moon Rise Moon Set Moon Rise Moon Set - - - - - - - 1st – 8:54am 20th – 12:16pm (ESE) 20th – 10:46pm 1st – 4:52pm 2nd – 9:56am 21st – 12:33pm 21st – 11:55pm 2nd – 5:36pm 3rd – 10:50am 22nd – 12:48pm (E) 23rd – 1:02am (W) 3rd – 6:31pm 4th – 11:35am 23rd – 1:03pm 24th – 2:09am 4th – 7:37pm 5th – 12:10pm 24th – 1:18pm 25th – 3:16am 5th – 8:50pm 6th – 12:38pm 25th – 1:35pm (ENE) 26th – 4:24am (WNW) 6th – 10:07pm (ENE) 7th – 1:01pm (WNW) 26th – 1:55pm 27th – 5:33am 7th – 11:26pm 8th – 1:21pm 27th – 2:19pm 28th – 6:41am 9th – 12:46am 9th – 1:39pm (W) 28th – 2:50pm 29th – 7:46am 10th – 2:08am (E) 10th – 1:58pm 29th – 3:31pm 30th – 8:44am 11th – 3:32am 11th – 2:18pm 30th – 4:23pm 31st – 9:33am 12th – 4:58am (ESE) 12th – 2:42pm (WSW) 31st – 5:27pm - - - - - - - 13th – 6:26am 13th – 3:13pm - - - - - - - Moon Phases 14th – 7:51am 14th – 3:53pm All times Last Quarter – 8th 15th – 9:07am 15th – 4:45pm in notes are set New Moon – 14th 16th – 10:09am 16th – 5:50pm for First Quarter – 21st 17th – 10:56am 17th – 7:03pm Somerton Full Moon – 30th 18th – 11:30am 18th – 8:19pm unless stated 19th – 11:56am +4.5 19th – 9:34pm (WSW) A useful site: www.heavens- A S Zielonka above.com There is a planned launch (no earlier than December) of SpaceX CRS-21 Cargo mission to the International Space Station (ISS). -
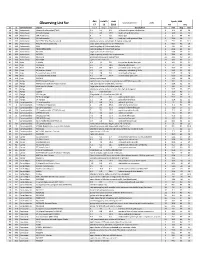
Observing List
day month year Epoch 2000 local clock time: 2.00 Observing List for 17 11 2019 RA DEC alt az Constellation object mag A mag B Separation description hr min deg min 58 286 Andromeda Gamma Andromedae (*266) 2.3 5.5 9.8 yellow & blue green double star 2 3.9 42 19 40 283 Andromeda Pi Andromedae 4.4 8.6 35.9 bright white & faint blue 0 36.9 33 43 48 295 Andromeda STF 79 (Struve) 6 7 7.8 bluish pair 1 0.1 44 42 59 279 Andromeda 59 Andromedae 6.5 7 16.6 neat pair, both greenish blue 2 10.9 39 2 32 301 Andromeda NGC 7662 (The Blue Snowball) planetary nebula, fairly bright & slightly elongated 23 25.9 42 32.1 44 292 Andromeda M31 (Andromeda Galaxy) large sprial arm galaxy like the Milky Way 0 42.7 41 16 44 291 Andromeda M32 satellite galaxy of Andromeda Galaxy 0 42.7 40 52 44 293 Andromeda M110 (NGC205) satellite galaxy of Andromeda Galaxy 0 40.4 41 41 56 279 Andromeda NGC752 large open cluster of 60 stars 1 57.8 37 41 62 285 Andromeda NGC891 edge on galaxy, needle-like in appearance 2 22.6 42 21 30 300 Andromeda NGC7640 elongated galaxy with mottled halo 23 22.1 40 51 35 308 Andromeda NGC7686 open cluster of 20 stars 23 30.2 49 8 47 258 Aries 1 Arietis 6.2 7.2 2.8 fine yellow & pale blue pair 1 50.1 22 17 57 250 Aries 30 Arietis 6.6 7.4 38.6 pleasing yellow pair 2 37 24 39 59 253 Aries 33 Arietis 5.5 8.4 28.6 yellowish-white & blue pair 2 40.7 27 4 59 239 Aries 48, Epsilon Arietis 5.2 5.5 1.5 white pair, splittable @ 150x 2 59.2 21 20 46 254 Aries 5, Gamma Arietis (*262) 4.8 4.8 7.8 nice bluish-white pair 1 53.5 19 18 49 258 Aries 9, Lambda Arietis -

Astronomie Pentru Şcolari
NICU GOGA CARTE DE ASTRONOMIE Editura REVERS CRAIOVA, 2010 Referent ştiinţific: Prof. univ.dr. Radu Constantinescu Editura Revers ISBN: 978-606-92381-6-5 2 În contextul actual al restructurării învăţământului obligatoriu, precum şi al unei manifeste lipse de interes din partea tinerei generaţii pentru studiul disciplinelor din aria curiculară Ştiinţe, se impune o intensificare a activităţilor de promovare a diferitelor discipline ştiinţifice. Dintre aceste discipline Astronomia ocupă un rol prioritar, având în vedere că ea intermediază tinerilor posibilitatea de a învăţa despre lumea în care trăiesc, de a afla tainele şi legile care guvernează Universul. În plus, anul 2009 a căpătat o co-notaţie specială prin declararea lui de către UNESCO drept „Anul Internaţional al Astronomiei”. În acest context, domnul profesor Nicu Goga ne propune acum o a doua carte cu tematică de Astronomie. După apariţia lucrării Geneza, evoluţia şi sfârşitul Universului, un volum care s+a bucurat de un real succes, apariţia lucrării „Carte de Astronomie” reprezintă un adevărat eveniment editorial, cu atât mai mult cu cât ea constitue în acelaşi timp un material monografic şi un material cu caracter didactic. Cartea este structurată în 13 capitole, trecând în revistă problematica generală a Astronomiei cu puţine elemente de Cosmologie. Cartea îşi propune şi reuşeşte pe deplin să ofere răspunsuri la câteva întrebări fundamentale şi tulburătoare legate de existenţa fiinţei umane şi a dimensiunii cosmice a acestei existenţe, incită la dialog şi la dorinţa de cunoaştere. Consider că, în ansamblul său, cartea poate contribui la îmbunătăţirea educaţiei ştiinţifice a tinerilor elevi şi este deosebit de utilă pentru toţi „actorii” implicaţi în procesul de predare-învăţare: elevi, părinţi, profesori. -

The Skyscraper 2008 01.Indd
The Skyscraper Vol. 35 no. 1 The monthly publication of The Skyscraper January 2008 January Meeting & Member Presentations FRIDAY, JANUARY 4TH AT NORTH SCITUATE COMMUNITY CENTER Remote and Robotic Observatories, Observe While You Sleep by Bob Napier Amateur Astronomical Society of Rhode Island 3D Astronomy presentation by Gerry Dyck 47 Peeptoad Road North Scituate, RI 02857 40 Years of Comet Observing www.theskyscrapers.org by Rick Lynch President Glenn Jackson DIRECTIONS TO THE COMMUNITY CENTER: From Seagrave Observatory: North 1st Vice President Scituate Community Center is the first building on the right side going Steve Hubbard south on Rt. 116, after the intersection of Rt. 6 Bypass (also Rt. 101) and 2nd Vice President Rt. 116, in N. Scituate. Famous Pizza is on the corner of that intersection. Kathy Siok Parking is across the street from the Community Center. Secretary Nichole Mechnig ANUARY IN THIS ISSUE Treasurer J 2008 PRESIDENT’S MESSAGE 2 Jim Crawford 7:30PM January Meeting North Scituate Community Glenn Jackson F4RIDAY Members at Large Center METEOR SHOWER 2 Jim Brenek PROSPECTS FOR 2008 Joe Sarandrea 7:00PM Public Observing Night Dave Huestis Seagrave Observatory, WINTER DOUBLE STARS: 3 Trustees SATURDAY5 weather permitting GEMINI Tracey Haley Glenn Chaple Bob Horton 7:00PM Public Observing Night Jerry Jeffrey Seagrave Observatory, ULTRAVIOLET SURPRISE 4 PATRICK L. BARRY & TONY S12ATURDAY weather permitting Librarian PHILLIP S Tom Barbish 7:00PM Public Observing Night DECEMBER MEETING 5 Editor Seagrave Observatory, NOTES STEVE HUB B ARD Jim Hendrickson S19ATURDAY weather permitting TREASURER’S REPORT 5 7:00PM Public Observing Night See back page for directions to JIM CRAW FORD Seagrave Observatory, Seagrave Observatory. -

NCRAL Northern Lights Spring 2021
to continue serving as Northern Lights newsletter editor if the INSIDE THIS ISSUE OF Northern Lights new Regional Chair deems that desirable. The Region needs individuals willing to stand for election NCRAL Chair’s Message…..............................……………………1 to the following positions for our May election: Chair and Vice NCRAL Elections Online May 7-8, 2021…………………………….2 Chair. The terms of the current office holders – yours truly Basic NCRAL Officer Job Responsibilities…..…………….……….3 and Bill Davidson, expire on May 8th. Our present Secretary- NCRAL Financial Statement Winter 2021……..…………….……4 Treasurer, Roy Gustafson, is willing to stand for election to Pike River Starfest……………………..…………………….……..………4 complete the term to which he was appointed last spring after Call for 2021 NCRAL Nominations & Applications……….......5 NCRAL 2020 was postponed. Others may stand for election to NCRAL Seasonal Messier Marathon Awards…………….………7 this office too if they are desirous of completing the one-year Noteworthy!……………………………………………………………………7 unexpired term of the current office holder. Bill Davidson, our A Homebuilt Solar Wind Magnetometer………………..………..7 Regional Representative to the Astronomical League, Venus: Evening Star 2021 by Jeffrey L. Hunt………………..….10 continues in this position unless he should become Chair. Astronomical League 75th Anniversary Coming……..…….…18 This year’s elections will be conducted electronically with Future NCRAL Conventions…………………………………..…….….19 special electors. I sent out an email notice on February 22nd Seasonal Messier Mini Marathon Observing Program……19 about the election procedures to be followed in the event of Add Your Email Address to NCRAL Member Database…...20 not holding an annual business meeting. (That email is NCRAL Website………………………………………………………….….20 repeated starting on page 2 of this newsletter.) Procedures Regional Officer & Leader Contact Information………..……21 are stipulated by the Region’s Bylaws. -

January 2020 BRAS Newsletter
A Monthly Meeting January 13th at 7PM at HRPO (Monthly meetings are on 2nd Mondays, Highland Road Park Observatory). Presentation: “A year in review and a planning and strategy session”. What's In This Issue? President’s Message Secretary's Summary Outreach Report Asteroid and Comet News Light Pollution Committee Report Globe at Night Member’s Corner - Coy and Lindsey’s Wedding Messages from the HRPO Friday Night Lecture Series Science Academy Solar Viewing Stem Expansion Plus Night Adult Astronomy Courses: Learn Your Sky, Learn Your Telescope, Learn Your Binoculars Observing Notes: Orion – The Hunter & Mythology Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society Baton Rouge Astronomical Society Newsletter, Night Visions Page 2 of 26 January 2020 President’s Message From our incoming President, Scott Cadwallader: Greetings one and all and welcome to the start of the New Year! We have some exciting things planned for the coming year, and, hopefully, this newsletter will get us going on the right foot. Inside, you’ll find several opportunities to reach out to the community and share the wonders of the night sky, even from our heavily light- polluted neck of the woods. In recent years, most of our activities have seemed to coalesce around our outreach events, so that, plus club meetings, have been our goto in terms of getting to know our fellow club members and our group learning activities. Particularly useful in this respect is what we do to assist BREC in running our observatory—Chris Kersey has details here and can help get you credentialled for that. -
January-March Objects Paging
January-March Objects in Turn Left at Orion , 5th edition (by page in the book) Page Name Constellation Type RA Dec. 52 M42, Orion Orion Diffuse Nebula 5 H 35.3 min. −5° 25' 52 M43, M42 cmpanio Orion Diffuse Nebula 5 H 35.6 min. −5° 16' 53 NGC 1980 Orion Diffuse Nebula 5 H 35.4 min. −4° 54' 53 NGC 1981 Orion Open Cluster 5 H 35.1 min. −5° 25' 54 Iota Orionis Orion Multiple Star 5 H 35.4 min. −5° 54' 54 Struve 745 Orion Double Star 5 H 34.7 min. −6° 0' 54 Struve 747 Orion Double Star 5 H 35 min. −6° 0' 55 BM Orionis Orion Variable Star 5 H 35.3 min. −5° 23' 55 Theta-1 Orionis, Trapezium Orion Multiple Star 5 H 35.3 min. −5° 25' 55 Theta-2 Orionis Orion Double Star 5 H 35.4 min. −5° 26' 55 V1016 Orionis Orion Variable Star 5 H 35.3 min. −5° 23' 56 Sigma Orionis Orion Multiple Star 5 H 38.7 min. −2° 36' 56 Struve 761 Orion Multiple Star 5 H 38.6 min. −2° 34' 58 32 Orionis Orion Double Star 5 H 30.8 min. 5° 57' 58 42 Orionis Orion Double Star 5 H 35.4 min. −4° 50' 58 52 Orionis Orion Double Star 5 H 48 min. 6° 27' 58 Beta Orionis, Rigel Orion Double Star 5 H 14.5 min. −8° 12' 58 Delta Orionis, Mintaka Orion Double Star 5 H 32 min. 0° 20' 58 Eta Orionis Orion Double Star 5 H 24.5 min. -

The Observer of the Twin City Amateur Astronomers
THE OBSERVER OF THE TWIN CITY AMATEUR ASTRONOMERS Volume 46, Number 2 February 2021 INSIDE THIS ISSUE: 1 Editor’s Choice: Image of the Month – M42 & Bernie 2 President’s Note 3 Calendar of Astronomical Events – February 2021 3 New & Renewing Members/Dues Blues/E-Mail List 4 This Month’s Phases of the Moon 4 This Month’s Solar Phenomena 4 Minutes of the January 5 TCAA BoD Meeting 5 Agenda Set for February 6th TCAA Annual Meeting 6 AstroBits – News from Around the TCAA 6 The Central Illinois Photometry Connection 6 Winter Mood 8 Wynken, Blynken and Nod – Eugene Field 9 A Homebuilt Solar Wind Magnetometer – Tim Stone 11 February 2021 with Jeffrey L. Hunt 17 Public Viewing Sessions for 2021 18 TCAA Monthly Club Meetings to Resume in March 19 Unwanted TCAA Assets – FINAL NOTICE! 20 Did You Know? 20 TCAA Treasurer’s Report as of January 28, 2021 The TCAA is an affiliate of the Astronomical League as well as its North Central Region. For more information about the TCAA, be certain to visit the TCAA website at http://www.tcaa.us/ Visit http://www.astroleague.org for additional information about the Astronomical League and its numerous membership benefits, including observing programs. EDITOR’S CHOICE: IMAGE OF THE MONTH – M42 & BERNIE Also, visit the NCRAL website at This month’s image includes the popular meme of “Find http://ncral.wordpress.com for in- Bernie.” Bernie Sanders has been seen everywhere since formation about our North Central Inauguration Day, and The OBSERVER is no exception. Can Region.