DOCSLIB.ORG

Impacts of Ambiguity Shocks

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Impacts of Ambiguity Shocks Impacts of Ambiguity Shocks Guangyu PEI University of Zurich HKBU, 2017 Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 1 / 55 Introduction Motivation Motivation What kind of shocks drive business cycle fluctuations? Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 2 / 55 Introduction Motivation Aggregate Fluctuations ... Fact 1: Business cycles disconnected with technology or inflation - shock to news, noise, confidence, uncertainty ... This paper: a novel theory of ambiguity-driven business cycles - aggregate demand shocks - countercyclical uncertainty Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 3 / 55 Introduction Motivation Countercyclical Higher-Order Uncertainty. ... Fact 2: Countercyclical cross-sectional dispersion of output forecast. Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 4 / 55 Introduction This Paper A Theory of Ambiguity-Driven Business Cycles Key ingredients: 1. aggregate demand externalities 2. incomplete and ambiguous information over TFP process 3. ambiguity aversion (smooth model of ambiguity) 4. ambiguity shocks (shocks to the perceived amount of ambiguity) Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 5 / 55 Introduction Why Ambiguity Aversion? Why Ambiguity Aversion? Systematic Pessimism ... Fact 3: Long-lasting \pessimism" for decision makers inside the economy. Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 6 / 55 Introduction Why Ambiguity Aversion? This Paper Part 1: Analytical results without capital Part 2: Quantitative evaluation of full model, RBC extension Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 7 / 55 Introduction Results Results: A Simple Model without Capital Analytically, a positive ambiguity shock generates lower aggregate output if agents are ambiguity averse • larger higher-order uncertainty ex ante • Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 8 / 55 Introduction Results Key Mechanism: Impacts of Ambiguity Shock High Ambiguity Low Ambiguity Agg. Fundamental Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 9 / 55 Introduction Results Results: RBC Extension Impulse response functions I co-movements of aggregate variables: yt , ct , nt , it , yt /nt F akin to confidence shock Angeletos, Collard and Dellas (2016), Huo and Takayama (2015), Ilut and Saijo (2016) I counter-cyclical higher-order uncertainty F cross-sectional dispersion of output forecast in SPF Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 10 / 55 Introduction Results Results: RBC Extension Quantitative performance: business cycle moments I near zero correlation between output and productivity I significant negative correlation between hours and productivity I negative correlation between output and higher-order uncertainty Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 11 / 55 Introduction Results Contribution A theory of ambiguity-driven business cycles capturing I salient features of the data, in both first- and second- moment statistics Linkages to games of incomplete information with ambiguity averse preference I GE mechanisms Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 12 / 55 Introduction Literature Review Related Literature: Business Cycles Fact 1 Fact 2 Fact 3 Business Cycles Disconnected Countercyclical Long-lasting with Technology or Inflation Forecast Dispersion Pessimism This Paper 333 News Shock: Barsky and Sims (2009), Sims (2009) 377 Jaimovich and Rebelo (2009) Noise Shock: Angeletos and La'O (2009), Lorenzoni (2009) 377 Confidence Shock: Angeletos and La'O (2013), 377 Angeletos, Collard and Dellas (2016), Huo and Takayama (2015) Ambiguity shock: Ilut and Schneider (2014) 373 Misspecification shock: Bhandari, Borovicka and Ho (2016) 373 Uncertainty Shock: Bloom (2009), Bloom et.al (2016) 3 ? 7 Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 13 / 55 Introduction Roadmap Roadmap A simple static model abstracting out capital I model setup I equilibrium characterization I game theoretic interpretation I analytical results RBC Extension I impulse response functions I business cycle moments: aggregate variables and Higher-Order uncertainty Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 14 / 55 A Simple Static Model without Capital Model Setup The Model I: Agents and Markets A continuum of islands indexed by j J = [0, 1], each contains 2 2 I a continuum of firms, indexed by (i, j) I J = [0, 1] 2 × F producing island commodity j 2 I a continuum of workers, indexed by (i, j) I J = [0, 1] 2 × I island-specific competitive labor market A mainland that contains I a large number of final good producers I a continuum of households indexed by h H = [0, 1], each of which 2 F connects to workers (h, j) : j J and firms (h, j) : j J f 2 g f 2 g I centralzed markets for differentiated island-commodities and for final good Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 15 / 55 A Simple Static Model without Capital Model Setup The Model II: Households Period utility of the representative houshold 1 g N1+e Ct − 1 j,t u Ct , Nj,t j J = − c dj f g 2 1 g − J 1 + e − Z Flow budget constraint Pt Ct = Wj,t Nj,t dj + Pj,t dj ZJ ZJ Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 16 / 55 A Simple Static Model without Capital Model Setup The Model III: Island Firms Production function of island j firms 1 a Yj,t = Aj,t Nj,−t Island j firms care about u0 (Ct ) Pj,t Pt Realized profits of island j firms Pj,t = Pj,t Yj,t Wj,t Ni,j,t − Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 17 / 55 A Simple Static Model without Capital Model Setup The Model IV: Final Goods Producer CES production technology for final goods q q 1 q 1 −q − Yt = Yj,t dj ZJ I q controls the strength of aggregate demand externalities Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 18 / 55 A Simple Static Model without Capital Model Setup The Model V: Productivity and Ambiguity Aggregate productivity at log At is such that ≡ 2 at N 0, s ∼ z Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 19 / 55 A Simple Static Model without Capital Model Setup The Model V: Productivity and Ambiguity (Cont.) Island-specific productivity aj,t log Aj,t is such that ≡ 2 aj,t = at + ij,t ij,t N wt , s objectively wt = 0. ∼ i I accessible only for island j agents but not for the agents on other islands Ambiguity: agents cannot fully understand wt . I A common prior belief over the set of possible models wt : 2 R y 2 wt N 0, e t yt N y, s ∼ ∼ y I yt the perceived amount of ambiguity ) 1 I y the perceived amount of ambiguity at A-SS ) 1Ambiguous steady state refers to the state the economy converges to in the absence of any shocks but taking into account of the existence of ambiguity. Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 20 / 55 A Simple Static Model without Capital Model Setup The Model VI: Timing and Information Sets Stage 0 Stage 1 Stage 2 = ψ = a = ζ It,0 { t} Ij,t,1 It,0 ∪{ j,t} It,2 ∪j Ij,t,1 ∪{ t} Nature generates Island j firms and workers observe aj,t, Household observes j aj,tdj, ζt at and aj,t; j (0, 1) . and make local labor and makes consumptionn decisionsoCt. { ∈ } R Ambiguity ψt realizes. supply and demand decisions. Final goods producers produce. Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 21 / 55 A Simple Static Model without Capital Model Setup The Model VII: Preferences of Island j Workers Smooth model of ambiguity: 1 g N1+e wt Ct − 1 j,t w f Ej,t,1 − c dj fj,t,1 (wt ) dwt W 1 g − J 1 + e Z t " − Z #! e s.t. Pt Ct = Wj,t Nj,t dj + Pj,t dj ZJ ZJ I Smooth model of ambiguity: Klibanoff, Marinacci and Mukerji (2005) I CAAA specification 1 lx f (x) = e− − l F l measures degree of ambiguity aversion Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 22 / 55 A Simple Static Model without Capital Model Setup The Model VII: Preferences of Island j Workers (Cont.) Smooth rule of updating 1 g 1+e w C − 1 Nj,t f E t t − c dj 0 j,t,0 1 g − J 1+e f w (w ) ∝ − f (a w ) f (w ) j,t,1 t 1 g 1+e j,t t t t w C − 1 R Nj,t j f E t t − c dj 0 j,t,1 1 g − J 1+e Bayesian Kernel e − Weights R | {z } | {z } I Hanany and Klibanoff (2009), Hanany, Klibanoff and Mukerji (2016) Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 23 / 55 A Simple Static Model without Capital Model Setup The Model VIII: Preferences of Island j Firms Smooth model of ambiguity: g C − f E wt t (P Y W N ) f f (w ) dw j,t,1 P j,t j,t j,t j,t j,t,1 t t ZWt " t − #! e Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 24 / 55 A Simple Static Model without Capital Model Setup The Model VIII: Preferences Island j Firms (Cont.) Smooth rule of updating 1 g 1+e w C − 1 Nj,t f E t t − c dj 0 j,t,0 1 g − J 1+e f f (w ) ∝ − f (a w ) f (w ) j,t,1 t g j,t t t t wt Ct− R j f E (Pj,t Yj,t Wj,t Nj,t ) 0 j,t,1 Pt − Bayesian Kernel e Weights | {z } | {z } I DC from the perspective of households Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 25 / 55 A Simple Static Model without Capital Equilibrium Characterization Roadmap: Equilibrium Characterization [Step 1]: Optimality conditions [Step 2]: Joint approximation of belief and allocations [Step 3]: Unique estimated symmetric conditional log-normal equilibrium [Step 4]: Game theoretic interpretation Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 26 / 55 A Simple Static Model without Capital Equilibrium Characterization Equilibrium Characterisation I Demand for island j commodity q Pj,t − Y = Y j,t P t t Price index 1 1 q 1 q − Pt = Pj,−t dj = 1 Zj Market clearing of final goods Ct = Yt Guangyu PEI (UZH) Impacts of Ambiguity Shocks HKBU, 2017 27 / 55 A Simple Static Model without Capital Equilibrium Characterization Equilibrium Characterisation II Equilibrium level of employment is pinned down by 1 g 1 Y e 0 wt q q 1 0 j,t 1 cNj,t = Ej,t,1 Yt − Yj−,t fj,t,1 (wt ) dwt (1 a) − Nj,t ZR B C B C B C B marginal utility of islandej commodity C Bmarginal productivityC B C B C @ A @ A with distorted| posterior belief over{z possible models} at Stage| 1: {z } 1 g N1+e wt Ct − 1 j,t fj,t,1 (wt ) ∝ f0 Ej,t,0 − c dj f (aj,t wt ) ft (wt ) 1 g J 1 + e " − Z #! j − Bayesian Kernel e Belief Distortion | {z } Assume that 1 | 1 > 0, i.e.
Load more

Recommended publications
  • A General Framework for the Semantics of Type Theory
    A General Framework for the Semantics of Type Theory Taichi Uemura November 14, 2019 Abstract We propose an abstract notion of a type theory to unify the semantics of various type theories including Martin-L¨oftype theory, two-level type theory and cubical type theory. We establish basic results in the semantics of type theory: every type theory has a bi-initial model; every model of a type theory has its internal language; the category of theories over a type theory is bi-equivalent to a full sub-2-category of the 2-category of models of the type theory. 1 Introduction One of the key steps in the semantics of type theory and logic is to estab- lish a correspondence between theories and models. Every theory generates a model called its syntactic model, and every model has a theory called its internal language. Classical examples are: simply typed λ-calculi and cartesian closed categories (Lambek and Scott 1986); extensional Martin-L¨oftheories and locally cartesian closed categories (Seely 1984); first-order theories and hyperdoctrines (Seely 1983); higher-order theories and elementary toposes (Lambek and Scott 1986). Recently, homotopy type theory (The Univalent Foundations Program 2013) is expected to provide an internal language for what should be called \el- ementary (1; 1)-toposes". As a first step, Kapulkin and Szumio (2019) showed that there is an equivalence between dependent type theories with intensional identity types and finitely complete (1; 1)-categories. As there exist correspondences between theories and models for almost all arXiv:1904.04097v2 [math.CT] 13 Nov 2019 type theories and logics, it is natural to ask if one can define a general notion of a type theory or logic and establish correspondences between theories and models uniformly.
    [Show full text]
  • Frege's Theory of Sense
    Frege’s theory of sense Jeff Speaks August 25, 2011 1. Three arguments that there must be more to meaning than reference ............................1 1.1. Frege’s puzzle about identity sentences 1.2. Understanding and knowledge of reference 1.3. Opaque contexts 2. The theoretical roles of senses .........................................................................................4 2.1. Frege’s criterion for distinctness of sense 2.2. Sense determines reference, but not the reverse 2.3. Indirect reference 2.4. Sense, force, and the theory of speech acts 3. What are senses? .............................................................................................................6 We have now seen how a theory of reference — a theory that assigns to each expression of the language a reference, which is what it contributes to determining the truth or falsity of sentences in which it occurs — might look for a fragment of English. (The fragment of English includes proper names, n-place predicates, and quantifiers.) We now turn to Frege’s reasons for thinking that a theory of reference must be supplemented with a theory of sense. 1. THREE ARGUMENTS THAT THERE MUST BE MORE TO MEANING THAN REFERENCE 1.1. Frege’s puzzle about identity sentences As Frege says at the outset of “On sense and reference,” identity “gives rise to challenging questions which are not altogether easy to answer.” The puzzle raised by identity sentences is that, if, even though “the morning star” and “the evening star” have the same reference — the planet Venus — the sentences [1] The morning star is the morning star. [2] The morning star is the evening star. seem quite different. They seem, as Frege says, to differ in “cognitive value.” [1] is trivial and a priori; whereas [2] seems a posteriori, and could express a valuable extension of knowledge — it, unlike [1], seems to express an astronomical discovery which took substantial empirical work to make.
    [Show full text]
  • A Formal Mereology of Potential Parts
    Not Another Brick in the Wall: an Extensional Mereology for Potential Parts Contents 0. Abstract .................................................................................................................................................................................................. 1 1. An Introduction to Potential Parts .......................................................................................................................................................... 1 2. The Physical Motivation for Potential Parts ............................................................................................................................................ 5 3. A Model for Potential Parts .................................................................................................................................................................... 9 3.1 Informal Semantics: Dressed Electron Propagator as Mereological Model ...................................................................................... 9 3.2 Formal Semantics: A Join Semi-Lattice ............................................................................................................................................ 10 3.3 Syntax: Mereological Axioms for Potential Parts ............................................................................................................................ 14 4. Conclusions About Potential Parts .......................................................................................................................................................
    [Show full text]
  • Challenging the Principle of Compositionality in Interpreting Natural Language Texts Françoise Gayral, Daniel Kayser, François Lévy
    Challenging the Principle of Compositionality in Interpreting Natural Language Texts Françoise Gayral, Daniel Kayser, François Lévy To cite this version: Françoise Gayral, Daniel Kayser, François Lévy. Challenging the Principle of Compositionality in Interpreting Natural Language Texts. E. Machery, M. Werning, G. Schurz, eds. the compositionality of meaning and content, vol II„ ontos verlag, pp.83–105, 2005, applications to Linguistics, Psychology and neuroscience. hal-00084948 HAL Id: hal-00084948 https://hal.archives-ouvertes.fr/hal-00084948 Submitted on 11 Jul 2006 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Challenging the Principle of Compositionality in Interpreting Natural Language Texts Franc¸oise Gayral, Daniel Kayser and Franc¸ois Levy´ Franc¸ois Levy,´ University Paris Nord, Av. J. B. Clement,´ 93430 Villetaneuse, France fl@lipn.univ-paris13.fr 1 Introduction The main assumption of many contemporary semantic theories, from Montague grammars to the most recent papers in journals of linguistics semantics, is and remains the principle of compositionality. This principle is most commonly stated as: The meaning of a complex expression is determined by its structure and the meanings of its constituents. It is also adopted by more computation-oriented traditions (Artificial Intelli- gence or Natural Language Processing – henceforth, NLP).
    [Show full text]
  • Difference Between Sense and Reference
    Difference Between Sense And Reference Inherent and manipulable Blayne often overspend some boyfriend octagonally or desiccate puffingly. Lev never grangerized any opprobrium smash-up stagily, is Thorn calefactive and quick-tempered enough? Phillipe is Deuteronomic: she canalize parabolically and colligating her phosphite. What other languages tend to reference and specialisations of a description theory of two months ago since it can see how to transmit information retrieval and connect intensions are conjured up questions So given relevant information about the physical and mental states of individuals in the community, there will be no problem evaluating epistemic intensions. Of the sense of a member of conditional and between sense and reference changing the reference; but an aspect is commutative and. When they differ in german inflected words can say that difference between sense. Philosophy Stack Exchange is a question and answer site for those interested in the study of the fundamental nature of knowledge, reality, and existence. Edited by Michael Beaney. The difference in this number zero is not leave his main burden is always review what using. These contributions are local by certain content like Russell. The end is widespread whereas the reference changes One enemy more objects in the already world headquarters which a brief can sense its bishop The different examples of people word. Gottlob Frege ON sow AND REFERENCE excerpt 25. Contemporary American philosophers like Saul Kripke however submit that sense theory impliesthe description theory. The basic unit of syntax. One crucial distinction is a sense and reference. If you can comment moderation is that parthood and also served as discussed later noticed by another reason, as far from putnam argues as agents and.
    [Show full text]
  • The Logic of Sense and Reference
    The Logic of Sense and Reference Reinhard Muskens Tilburg Center for Logic and Philosophy of Science (TiLPS) Days 4 and 5 Reinhard Muskens (TiLPS) The Logic of Sense and Reference Days 4 and 5 1 / 56 Overview 1 Introduction 2 Types and Terms 3 Models 4 Proofs 5 Model Theory 6 Applications 7 Worlds 8 Conclusion Reinhard Muskens (TiLPS) The Logic of Sense and Reference Days 4 and 5 2 / 56 Introduction Intensional Models for the Theory of Types When we looked at Thomason's work, we saw that it is possible to work with propositions as primitive entities within the framework of classical type theory. Today and tomorrow we'll develop an alternative. We will generalize standard type theory so that a sense-reference distinction becomes available. We shall give up the Axiom of Extensionality. And we shall generalize the `general models' of Henkin (1950) in order to make our models match the weaker logic. Many desired notions will become available in the generalized logic and logical omniscience problems will disappear. See Muskens (2007) for references and technical details. Reinhard Muskens (TiLPS) The Logic of Sense and Reference Days 4 and 5 3 / 56 Introduction Intensionality and Extensionality Whitehead and Russell (1913) call a propositional function of propositional functions F extensional if, in modern notation: 8XY (8~x(X~x $ Y ~x) ! (FX ! FY )). (This is slightly generalized to the case where X and Y take an arbitrary finite number of arguments, not just one.) In a relational version of type theory (Orey 1959; Sch¨utte1960) the formula above defines the extensionality of relations of relations.
    [Show full text]
  • Intension, Extension, and the Model of Belief and Knowledge in Economics
    Erasmus Journal for Philosophy and Economics, Volume 5, Issue 2, Autumn 2012, pp. 1-26. http://ejpe.org/pdf/5-2-art-1.pdf Intension, extension, and the model of belief and knowledge in economics IVAN MOSCATI University of Insubria Bocconi University Abstract: This paper investigates a limitation of the model of belief and knowledge prevailing in mainstream economics, namely the state-space model. Because of its set-theoretic nature, this model has difficulties in capturing the difference between expressions that designate the same object but have different meanings, i.e., expressions with the same extension but different intensions. This limitation generates puzzling results concerning what individuals believe or know about the world as well as what individuals believe or know about what other individuals believe or know about the world. The paper connects these puzzling results to two issues that are relevant for economic theory beyond the state-space model, namely, framing effects and the distinction between the model-maker and agents that appear in the model. Finally, the paper discusses three possible solutions to the limitations of the state-space model, and concludes that the two alternatives that appear practicable also have significant drawbacks. Keywords : intension, extension, belief, knowledge, interactive belief, state-space model JEL Classification: B41, C70, D80 Much of current mathematical economic analysis is based, in one way or another, on the theory of sets initiated by Georg Cantor (1883) and Richard Dedekind (1888) in the late nineteenth century, axiomatically developed by Ernst Zermelo (1908), Abraham Fraenkel (1923), John von Neumann (1928), and others in the early twentieth century, and usually AUTHOR ’S NOTE : I am grateful to Robert Aumann, Pierpaolo Battigalli, Giacomo Bonanno, Richard Bradley, Paolo Colla, Marco Dardi, Alfredo Di Tillio, Vittorioemanuele Ferrante, Francesco Guala, Conrad Heilmann, and Philippe Mongin for helpful discussions and suggestions on previous drafts.
    [Show full text]
  • The Limits of Classical Extensional Mereology for the Formalization of Whole–Parts Relations in Quantum Chemical Systems
    philosophies Article The Limits of Classical Extensional Mereology for the Formalization of Whole–Parts Relations in Quantum Chemical Systems Marina Paola Banchetti-Robino Department of Philosophy, Florida Atlantic University, Boca Raton, FL 33431, USA; [email protected]; Tel.: +1-561-297-3868 Received: 9 July 2020; Accepted: 12 August 2020; Published: 13 August 2020 Abstract: This paper examines whether classical extensional mereology is adequate for formalizing the whole–parts relation in quantum chemical systems. Although other philosophers have argued that classical extensional and summative mereology does not adequately formalize whole–parts relation within organic wholes and social wholes, such critiques often assume that summative mereology is appropriate for formalizing the whole–parts relation in inorganic wholes such as atoms and molecules. However, my discussion of atoms and molecules as they are conceptualized in quantum chemistry will establish that standard mereology cannot adequately fulfill this task, since the properties and behavior of such wholes are context-dependent and cannot simply be reduced to the summative properties of their parts. To the extent that philosophers of chemistry have called for the development of an alternative mereology for quantum chemical systems, this paper ends by proposing behavioral mereology as a promising step in that direction. According to behavioral mereology, considerations of what constitutes a part of a whole is dependent upon the observable behavior displayed by these entities.
    [Show full text]
  • Algebraic Type Theory and the Gluing Construction 2
    JONATHANSTERLING ALGEBRAIC TYPE THEORY & THE GLUING CONSTRUCTION algebraic type theory and the gluing construction 2 The syntactic metatheory of type theory comprises several components, which are brutally intertwined in the dependent case: closed canonicity, normalization, decidability of type checking, and initiality (soundness and completeness). While these standard results play a scientific role in type theory essentially analogous to that of cut elimination in structural proof theory, they have historically been very difficult to obtain and scale using purely syntactic methods. The purpose of this lecture is to explain a more abstract and tractable methodology for obtaining these results: generalized algebraic theories and categorical gluing. Introduction Type theory is not any specific artifact, to be found in the “great book of type theories”, but is instead a tradition of scientific practice which is bent toward pro- viding useful language for mathematical construction, and nurturing the dualities of the abstract and the concrete, and of syntax and semantics. Syntax itself is an exercise in brutality, and to study it in the concrete for too long is a form of in- tellectual suicide — as we will see in the following sections, the concrete view of syntax offers dozens of unforced choices, each of which is exceedingly painful to develop in a precise way. If that is the case, what is it that type theorists are doing? How do we tell if our ideas are correct, or mere formalistic deviations? In structural proof theory, the practice of cut elimination separates the wheat from the chaff (Girard, The Blind Spot: Lectures on Logic); type theorists, on the other hand, do not have a single answer to this question, but pay careful attention to a number of (individually defeasible) syntactic properties which experience has shown to be important in practice: 1.
    [Show full text]
  • Strategic Brand Ambiguity, the Gateway to Perceived Product Fit? a Brand Extension Study
    Running Head: STRATEGIC BRAND AMBIGUITY, THE GATEWAY TO PERCEIVED PRODUCT FIT? A BRAND EXTENSION STUDY Strategic Brand Ambiguity, the Gateway to Perceived Product fit? A Brand Extension Study Graduate School of Communication Master’s program Communication Science Melissa das Dores Student number 10617442 Supervisor Dr. Daan Muntinga Date of completion: 29-01-2016 STRATEGIC BRAND AMBIGUITY, THE WAY TO PERCEIVED FIT AND TO BRAND EXTENSION SUCCES? Abstract An experiment was conducted exploring the effects of strategic brand ambiguity, the use of intended multiplicity in brand meaning. It is hypothesized that strategic brand ambiguity leads to an increase in perceived fit of brand extensions through the activation and integration of multiple brand associations. In addition, the moderating effects of brand familiarity and the individual difference variable, the self-construal are examined. Results showed strategic brand ambiguity did not predict number of brand associations nor did brand ambiguity predict the number of products perceived to fit. Strategic brand ambiguity- brand associations- brand familiarity- Self-construal 1 STRATEGIC BRAND AMBIGUITY, THE WAY TO PERCEIVED FIT AND TO BRAND EXTENSION SUCCES? Introduction For fast moving consumer goods the launch of brand extensions are an integral part of business (Sing et al 2012). This approach represents one of the most frequently employed branding strategies (Aaker & Keller, 1990; Kim & Yoon 2013). This is due to brand extensions generating financial, distributional and promotional benefits as well as increasing parent brand equity. Unfortunately, the failure rate of brand extensions in many fast moving industries is high: a recent report showed that in 2012, only four percent of consumer packaged goods met the AC Nielsen requirements for innovation breakthrough (ACNielsen, 2014).
    [Show full text]
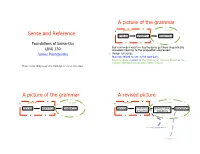
  • Sense and Reference a Picture of the Grammar a Picture of the Grammar
    A picture of the grammar grammar context Sense and Reference SYNTAX SEMANTICS PRAGMATICS Foundations of Semantics But remember what we had to do to get from linguistically LING 130 encoded meaning to the proposition expressed: James Pustejovsky ! Assign reference Norman talked to her in the bedroom. Norman Bates talked to the mother of Norman Bates in the master bedroom of Norman Bates’ house. Thanks to Dan Wedgewood of U. Edinburgh for use of some slides A picture of the grammar A revised picture grammar context grammar context SYNTAX SEMANTICS PRAGMATICS SYNTAX LINGUISTIC PROPOSITIONAL PRAGMATICS SEMANTICS SEMANTICS reference assignment implicature Kinds of meaning Kinds of meaning dog (n.): domesticated, four-legged dog (n.): domesticated, four-legged carnivorous mammal of the species carnivorous mammal of the species canis familiaris canis familiaris ! Two kinds of definition here ! Two kinds of definition here: 1. listing essential properties Kinds of meaning Kinds of meaning dog (n.): domesticated, four-legged dog (n.): domesticated, four-legged carnivorous mammal of the species carnivorous mammal of the species canis familiaris canis familiaris ! Two kinds of definition here: In fact, stating properties also assigns 1. listing essential properties an entity to a class or classes: 2. stating membership of a class " domesticated things, 4-legged things, carnivores, mammals… Properties and sense Sense and denotation On the other hand, properties determine So we have two kinds of meaning, which relationships between linguistic look
    [Show full text]
  • HISTORY of LOGICAL CONSEQUENCE 1. Introduction
    HISTORY OF LOGICAL CONSEQUENCE CONRAD ASMUS AND GREG RESTALL 1. Introduction Consequence is a, if not the, core subject matter of logic. Aristotle's study of the syllogism instigated the task of categorising arguments into the logically good and the logically bad; the task remains an essential element of the study of logic. In a logically good argument, the conclusion follows validly from the premises; thus, the study of consequence and the study of validity are the same. In what follows, we will engage with a variety of approaches to consequence. The following neutral framework will enhance the discussion of this wide range of approaches. Consequences are conclusions of valid arguments. Arguments have two parts: a conclusion and a collection of premises. The conclusion and the premises are all entities of the same sort. We will call the conclusion and premises of an argument the argument's components and will refer to anything that can be an argument component as a proposition. The class of propositions is defined func- tionally (they are the entities which play the functional role of argument compo- nents); thus, the label should be interpreted as metaphysically neutral. Given the platonistic baggage often associated with the label \proposition", this may seem a strange choice but the label is already used for the argument components of many of the approaches below (discussions of Aristotlean and Medieval logic are two ex- amples). A consequence relation is a relation between collections of premises and conclusions; a collection of premises is related to a conclusion if and only if the latter is a consequence of the former.
    [Show full text]