Radiowave Propagation 1 Introduction Wireless Communication Relies on Electromagnetic Waves to Carry Information from One Point to Another
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Basic Statistics Range, Mean, Median, Mode, Variance, Standard Deviation
Kirkup Chapter 1 Lecture Notes SEF Workshop presentation = Science Fair Data Analysis_Sohl.pptx EDA = Exploratory Data Analysis Aim of an Experiment = Experiments should have a goal. Make note of interesting issues for later. Be careful not to get side-tracked. Designing an Experiment = Put effort where it makes sense, do preliminary fractional error analysis to determine where you need to improve. Units analysis and equation checking Units website Writing down values: scientific notation and SI prefixes http://en.wikipedia.org/wiki/Metric_prefix Significant Figures Histograms in Excel Bin size – reasonable round numbers 15-16 not 14.8-16.1 Bin size – reasonable quantity: Rule of Thumb = # bins = √ where n is the number of data points. Basic Statistics range, mean, median, mode, variance, standard deviation Population, Sample Cool trick for small sample sizes. Estimate this works for n<12 or so. √ Random Error vs. Systematic Error Metric prefixes m n [n 1] Prefix Symbol 1000 10 Decimal Short scale Long scale Since 8 24 yotta Y 1000 10 1000000000000000000000000septillion quadrillion 1991 7 21 zetta Z 1000 10 1000000000000000000000sextillion trilliard 1991 6 18 exa E 1000 10 1000000000000000000quintillion trillion 1975 5 15 peta P 1000 10 1000000000000000quadrillion billiard 1975 4 12 tera T 1000 10 1000000000000trillion billion 1960 3 9 giga G 1000 10 1000000000billion milliard 1960 2 6 mega M 1000 10 1000000 million 1960 1 3 kilo k 1000 10 1000 thousand 1795 2/3 2 hecto h 1000 10 100 hundred 1795 1/3 1 deca da 1000 10 10 ten 1795 0 0 1000 -

Common Units Facilitator Instructions
Common Units Facilitator Instructions Activities Overview Skill: Estimating and verifying the size of Participants discuss, read, and practice using one or more units commonly-used units, and developing personal of measurement found in environmental science. Includes a fact or familiar analogies to describe those units. sheet, and facilitator guide for each of the following units: Time: 10 minutes (without activity) 20-30 minutes (with activity) • Order of magnitude • Metric prefixes (like kilo-, mega-, milli-, micro-) [fact sheet only] Preparation 3 • Cubic meters (m ) Choose which units will be covered. • Liters (L), milliliters (mL), and deciliters (dL) • Kilograms (kg), grams (g), milligrams (mg), and micrograms (µg) Review the Fact Sheet and Facilitator Supplement for each unit chosen. • Acres and Hectares • Tons and Tonnes If doing an activity, note any extra materials • Watts (W), kilowatts (kW), megawatt (MW), kilowatt-hours needed. (kWh), megawatt-hours (mWh), and million-megawatt-hours Materials Needed (MMWh) [fact sheet only] • Parts per million (ppm) and parts per billion (ppb) Fact Sheets (1 per participant per unit) Facilitator Supplement (1 per facilitator per unit) When to Use Them Any additional materials needed for the activity Before (or along with) a reading of technical documents or reports that refer to any of these units. Choose only the unit or units related to your community; don’t use all the fact sheets. You can use the fact sheets by themselves as handouts to supple- ment a meeting or other activity. For a better understanding and practice using the units, you can also frame each fact sheet with the questions and/or activities on the corresponding facilitator supplement. -

Lesson 2: Scale of Objects Student Materials
Lesson 2: Scale of Objects Student Materials Contents • Visualizing the Nanoscale: Student Reading • Scale Diagram: Dominant Objects, Tools, Models, and Forces at Various Different Scales • Number Line/Card Sort Activity: Student Instructions & Worksheet • Cards for Number Line/Card Sort Activity: Objects & Units • Cutting it Down Activity: Student Instructions & Worksheet • Scale of Objects Activity: Student Instructions & Worksheet • Scale of Small Objects: Student Quiz 2-S1 Visualizing the Nanoscale: Student Reading How Small is a Nanometer? The meter (m) is the basic unit of length in the metric system, and a nanometer is one billionth of a meter. It's easy for us to visualize a meter; that’s about 3 feet. But a billionth of that? It’s a scale so different from what we're used to that it's difficult to imagine. What Are Common Size Units, and Where is the Nanoscale Relative to Them? Table 1 below shows some common size units and their various notations (exponential, number, English) and examples of objects that illustrate about how big each unit is. Table 1. Common size units and examples. Unit Magnitude as an Magnitude as a English About how exponent (m) number (m) Expression big? Meter 100 1 One A bit bigger than a yardstick Centimeter 10-2 0.01 One Hundredth Width of a fingernail Millimeter 10-3 0.001 One Thickness of a Thousandth dime Micrometer 10-6 0.000001 One Millionth A single cell Nanometer 10-9 0.000000001 One Billionth 10 hydrogen atoms lined up Angstrom 10-10 0.0000000001 A large atom Nanoscience is the study and development of materials and structures in the range of 1 nm (10-9 m) to 100 nanometers (100 x 10-9 = 10-7 m) and the unique properties that arise at that scale. -

Time and Frequency Users' Manual
,>'.)*• r>rJfl HKra mitt* >\ « i If I * I IT I . Ip I * .aference nbs Publi- cations / % ^m \ NBS TECHNICAL NOTE 695 U.S. DEPARTMENT OF COMMERCE/National Bureau of Standards Time and Frequency Users' Manual 100 .U5753 No. 695 1977 NATIONAL BUREAU OF STANDARDS 1 The National Bureau of Standards was established by an act of Congress March 3, 1901. The Bureau's overall goal is to strengthen and advance the Nation's science and technology and facilitate their effective application for public benefit To this end, the Bureau conducts research and provides: (1) a basis for the Nation's physical measurement system, (2) scientific and technological services for industry and government, a technical (3) basis for equity in trade, and (4) technical services to pro- mote public safety. The Bureau consists of the Institute for Basic Standards, the Institute for Materials Research the Institute for Applied Technology, the Institute for Computer Sciences and Technology, the Office for Information Programs, and the Office of Experimental Technology Incentives Program. THE INSTITUTE FOR BASIC STANDARDS provides the central basis within the United States of a complete and consist- ent system of physical measurement; coordinates that system with measurement systems of other nations; and furnishes essen- tial services leading to accurate and uniform physical measurements throughout the Nation's scientific community, industry, and commerce. The Institute consists of the Office of Measurement Services, and the following center and divisions: Applied Mathematics -

NSF Sensational 60
Cover credits Background: © 2010 JupiterImages Corporation Inset credits (left to right): Courtesy Woods Hole Oceanographic Institution; Gemini Observatory; Nicolle Rager Fuller, National Science Foundation; Zee Evans, National Science Foundation; Nicolle Rager Fuller, National Science Foundation; Zina Deretsky, National Science Foundation, adapted from map by Chris Harrison, Human-Computer Interaction Institute, Carnegie Mellon University; Tobias Hertel, Insti- tute for Physical Chemistry, University of Würzburg Design by: Adrian Apodaca, National Science Foundation 1 Introduction The National Science Foundation (NSF) is an independent federal agency that supports fundamental research and education across all fields of science and engineering. Congress passed legislation creating the NSF in 1950 and President Harry S. Truman signed that legislation on May 10, 1950, creating a government agency that funds research in the basic sciences, engineering, mathematics and technology. NSF is the federal agency responsible for nonmedical research in all fields of science, engineering, education and technology. NSF funding is approved through the federal budget process. In fiscal year (FY) 2010, its budget is about $6.9 billion. NSF has an independent governing body called the National Science Board (NSB) that oversees and helps direct NSF programs and activities. NSF funds reach all 50 states through grants to nearly 2,000 universities and institutions. NSF is the funding source for approximately 20 percent of all federally supported basic research conducted by America’s colleges and universities. Each year, NSF receives over 45,000 competitive requests for funding, and makes over 11,500 new funding awards. NSF also awards over $400 million in professional and service contracts yearly. NSF has a total workforce of about 1,700 at its Arlington, Va., headquarters, including approximately 1,200 career employees, 150 scientists from research institutions on temporary duty, 200 contract workers and the staff of the NSB office and the Office of the Inspector General. -

Inflationary Big Bang Cosmology and the New Cosmic Background Radiation Findings
Inflationary Big Bang Cosmology and the New Cosmic Background Radiation Findings By Richard M. Todaro American Physical Society June 2001 With special thanks to Dr. Paul L. Richards, Professor of Physics at the University of California, Berkeley for his kind and patient telephone tutorial on Big Bang cosmology. A trio of new findings lends strong support to a powerful idea called “inflation” that explains many of the observed characteristics of our universe. The findings relate to the slight variations in the faint microwave energy that permeates the cosmos. The size and distribution of these variations agree well with the theory of inflation, which holds that the entire universe underwent an incredibly brief period of mind-bogglingly vast expansion (a hyper-charged Big Bang) before slowing down to the slower rate of expansion observed today. Combining the new findings about the cosmic microwave background radiation with inflation, cosmologists (the scientists who study the origin of the cosmos) believe they also have a compelling explanation for why stars and galaxies have their irregular distribution across the observable universe. Some cosmologists now believe that not only is the irregular distribution of “ordinary matter” related to the nature of these variations in the cosmic background radiation, but through inflation, both are related to the conditions within that incredibly dense and hot universe at the instant of its creation. (Such ordinary matter includes the elements that make up our Sun and our Earth and, ultimately, human beings.) Cosmologists have long believed that every bit of matter in the entire observable Universe – all the planets, stars, and galaxies, which we can see through powerful telescopes, as well as all the things we can’t see directly but know must be there due to the effects they produce – was once compressed together into a very dense and very hot arbitrarily small volume. -

Mathematics 3-4
Mathematics 3-4 Mathematics Department Phillips Exeter Academy Exeter, NH August 2021 To the Student Contents: Members of the PEA Mathematics Department have written the material in this book. As you work through it, you will discover that algebra, geometry, and trigonometry have been integrated into a mathematical whole. There is no Chapter 5, nor is there a section on tangents to circles. The curriculum is problem-centered, rather than topic-centered. Techniques and theorems will become apparent as you work through the problems, and you will need to keep appropriate notes for your records | there are no boxes containing important theorems. There is no index as such, but the reference section that starts on page 103 should help you recall the meanings of key words that are defined in the problems (where they usually appear italicized). Problem solving: Approach each problem as an exploration. Reading each question care- fully is essential, especially since definitions, highlighted in italics, are routinely inserted into the problem texts. It is important to make accurate diagrams. Here are a few useful strategies to keep in mind: create an easier problem, use the guess-and-check technique as a starting point, work backwards, recall work on a similar problem. It is important that you work on each problem when assigned, since the questions you may have about a problem will likely motivate class discussion the next day. Problem solving requires persistence as much as it requires ingenuity. When you get stuck, or solve a problem incorrectly, back up and start over. Keep in mind that you're probably not the only one who is stuck, and that may even include your teacher. -

Powers of 10 & Scientific Notation
Physics 151 Powers of 10 & Scientific Notation In all of the physical sciences, we encounter many numbers that are so large or small that it would be exceedingly cumbersome to write them with dozens of trailing or leading zeroes. Since our number system is “base-10” (based on powers of 10), it is far more convenient to write very large and very small numbers in a special exponential notation called scientific notation. In scientific notation, a number is rewritten as a simple decimal multiplied by 10 raised to some power, n, like this: x.xxxx... × 10n Powers of Ten Remember that the powers of 10 are as follows: 0 10 = 1 1 –1 1 10 = 10 10 = 0.1 = 10 2 –2 1 10 = 100 10 = 0.01 = 100 3 –3 1 10 = 1000 10 = 0.001 = 1000 4 –4 1 10 = 10,000 10 = 0.0001 = 10,000 ...and so forth. There are some important powers that we use often: 103 = 1000 = one thousand 10–3 = 0.001 = one thousandth 106 = 1,000,000 = one million 10–6 = 0.000 001 = one millionth 109 = 1,000,000,000 = one billion 10–9 = 0.000 000 001 = one billionth 1012 = 1,000,000,000,000 = one trillion 10–12 = 0.000 000 000 001 = one trillionth In the left-hand columns above, where n is positive, note that n is simply the same as the number of zeroes in the full written-out form of the number! However, in the right-hand columns where n is negative, note that |n| is one greater than the number of place-holding zeroes. -
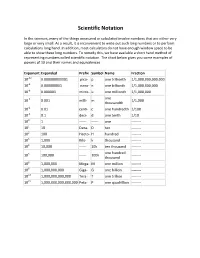
Scientific Notation
Scientific Notation In the sciences, many of the things measured or calculated involve numbers that are either very large or very small. As a result, it is inconvenient to write out such long numbers or to perform calculations long hand. In addition, most calculators do not have enough window space to be able to show these long numbers. To remedy this, we have available a short hand method of representing numbers called scientific notation. The chart below gives you some examples of powers of 10 and their names and equivalences. Exponent Expanded Prefix Symbol Name Fraction 10-12 0.000000000001 pico- p one trillionth 1/1,000,000,000,000 10-9 0.000000001 nano- n one billionth 1/1,000,000,000 10-6 0.000001 micro- u one millionth 1/1,000,000 one 10-3 0.001 milli- m 1/1,000 thousandth 10-2 0.01 centi- c one hundredth 1/100 10-1 0.1 deci- d one tenth 1/10 100 1 ------ ------ one -------- 101 10 Deca- D ten -------- 102 100 Hecto- H hundred -------- 103 1,000 Kilo- k thousand -------- 104 10,000 ------ 10k ten thousand -------- one hundred 105 100,000 ------ 100k -------- thousand 106 1,000,000 Mega- M one million -------- 109 1,000,000,000 Giga- G one billion -------- 1012 1,000,000,000,000 Tera- T one trillion -------- 1015 1,000,000,000,000,000 Peta- P one quadrillion -------- Powers of 10 and Place Value.......... Multiplying by 10, 100, or 1000 in the following problems just means to add the number of zeroes to the number being multiplied. -

Metric Measurements
Metric Measurements Background: When we use measurements such as millimeters, micrometers, and nanometers, students don’t necessarily have a good idea about how small these measurements are, nor do they realize the relative sizes of these different units. Materials: Several meter sticks or paper meter tapes Tape White board or wall Appropriate markers To Do and Notice: 1. Tape 1 meter stick to the board in the upper left-hand corner. 2. Label it “1 meter (m)”. 3. Discuss the other units on the meter stick – centimeters and millimeters. Explain the fractional relationships with centimeters and millimeters to 1 meter. Identify and label the 1000th millimeter. 4. Tape a second meter stick to the board below and slightly to the right of the first. 5. Explain that this meter stick represents an expanded version of the 1000th mm from the meter stick above. At this scale, we have our millimeter divided into thousandths. One 1000th of a millimeter is a micrometer, or µm. Notice that the micrometer is three orders of magnitude smaller than the millimeter, which is three orders of magnitude Lori Lambertson Exploratorium Teacher Institute Page 1 © 2008 Exploratorium, all rights reserved smaller than the meter. Therefore, one micrometer is 1/1,000,000 of a meter. Identify and label the 1000th µm. A micrometer is a millionth of a meter. How small is a micrometer? A human hair is approximately 100 micrometers in width. A red blood cell is approximately 10 micrometers in diameter, while your average bacterium is approximately 1 micrometer in diameter. 6. Tape the third meter stick to the board. -

Rare-Earth Elements
Rare-Earth Elements Chapter O of Critical Mineral Resources of the United States—Economic and Environmental Geology and Prospects for Future Supply Professional Paper 1802–O U.S. Department of the Interior U.S. Geological Survey Periodic Table of Elements 1A 8A 1 2 hydrogen helium 1.008 2A 3A 4A 5A 6A 7A 4.003 3 4 5 6 7 8 9 10 lithium beryllium boron carbon nitrogen oxygen fluorine neon 6.94 9.012 10.81 12.01 14.01 16.00 19.00 20.18 11 12 13 14 15 16 17 18 sodium magnesium aluminum silicon phosphorus sulfur chlorine argon 22.99 24.31 3B 4B 5B 6B 7B 8B 11B 12B 26.98 28.09 30.97 32.06 35.45 39.95 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 potassium calcium scandium titanium vanadium chromium manganese iron cobalt nickel copper zinc gallium germanium arsenic selenium bromine krypton 39.10 40.08 44.96 47.88 50.94 52.00 54.94 55.85 58.93 58.69 63.55 65.39 69.72 72.64 74.92 78.96 79.90 83.79 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 rubidium strontium yttrium zirconium niobium molybdenum technetium ruthenium rhodium palladium silver cadmium indium tin antimony tellurium iodine xenon 85.47 87.62 88.91 91.22 92.91 95.96 (98) 101.1 102.9 106.4 107.9 112.4 114.8 118.7 121.8 127.6 126.9 131.3 55 56 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 cesium barium hafnium tantalum tungsten rhenium osmium iridium platinum gold mercury thallium lead bismuth polonium astatine radon 132.9 137.3 178.5 180.9 183.9 186.2 190.2 192.2 195.1 197.0 200.5 204.4 207.2 209.0 (209) (210) (222) 87 88 104 105 106 107 108 109 110 111 112 113 114 115 -
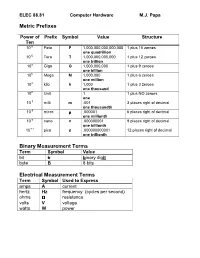
Metric Prefixes Binary Measurement Terms Electrical Measurement Terms
ELEC 88.81 Computer Hardware M.J. Papa Metric Prefixes Power of Prefix Symbol Value Structure Ten 10 15 Peta P 1,000,000,000,000,000 1 plus 15 zeroes one quadrillion 10 12 Tera T 1,000,000,000,000 1 plus 12 zeroes one trillion 10 9 Giga G 1,000,000,000 1 plus 9 zeroes one billion 10 6 Mega M 1,000,000 1 plus 6 zeroes one million 10 3 kilo k 1,000 1 plus 3 zeroes one thousand 10 0 Unit 1 1 plus NO zeroes one 10 -3 milli m .001 3 places right of decimal one thousandth 10 -6 micro µµµ .000001 6 places right of decimal one millionth 10 -9 nano n .000000001 9 places right of decimal one billionth 10 -12 pico p .000000000001 12 places right of decimal one trillionth Binary Measurement Terms Term Symbol Value bit b binary dig it byte B 8 bits Electrical Measurement Terms Term Symbol Used to Express amps A current hertz Hz frequency (cycles per second) ohms ΩΩΩ resistance volts V voltage watts W power ELEC 88.81 Computer Hardware M.J. Papa Converting Units Within the Metric System Using a Multiplication Factor Units can be converted by using a multiplication factor. Use of a multiplication factor results in simply moving the decimal point left or right. Use the table below to convert units. When Moving Left to Right Use Positive Power of Ten 10 12 10 9 10 6 10 3 10 0 10 -3 10 -6 10 -9 10 -12 tera giga mega kilo milli micro nano pico T G M k • m µ n p When Moving Right to Left Use Negative Power of Ten Example: Convert 50 mA to A.