User Bulletin 5 Determination of Material Properties
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Guide to Safety Procedures for Vertical Concrete Formwork
F401 Guide to Safety Procedures for Vertical Concrete Formwork SCAFFOLDING, SHORING AND FORMING INSTITUTE, INC. 1300 SUMNER AVENUE, CLEVELAND, OHIO 44115 (216) 241-7333 F401 F O R E W O R D The “Guide to Safety Procedures for Vertical Concrete Formwork” has been prepared by the Forming Section Engineering Committee of the Scaffolding, Shoring & Forming Institute, Inc., 1300 Sumner Avenue, Cleveland, Ohio 44115. It is suggested that the reader also refer to other related publications available from the Scaffolding, Shoring & Forming Institute. The SSFI welcomes any comments or suggestions regarding this publication. Contact the Institute at the following address: Scaffolding, Shoring and Forming Institute, 1300 Sumner Ave., Cleveland, OH 44115. i F401 CONTENTS PAGE Introduction ........................................................................................ 1 Section 1 - General................................................................................ 2 Section 2 - Erection of Formwork......................................................... 2 Section 3 - Bracing................................................................................ 3 Section 4 - Walkways/Scaffold Brackets.............................................. 3 Section 5 - Special Applications........................................................... 4 Section 6 - Inspection............................................................................ 4 Section 7 - Concrete Placing................................................................. 5 Section -

21851 Concrete Reinforcment Catalog
R EBAR Reinforcing bar or rebar is a hot rolled steel product used primarily for reinforcing concrete structures. Meeting ASTM specifications, rebar grades are available varying in yield strength, bend test requirements, composition. Grade 300 / Grade 40 Sizes Due to lower carbon content, grade 300 is easier Metric Bar Nominal Weight Weight to bend. Size Number Size Per Ft. Per 20' (lbs.) (lbs.) Typical applications: Residential construction 10 #3 3/8" (.3759) .376 7.52 Grade 420 / Grade 60 13 #4 1/2" (.5009) .668 13.36 Used in high stress rated applications: higher carbon 16 #5 5/8" (.6259) 1.043 20.86 content provides increased vertical strength. 19 #6 3/4" (.7509) 1.502 30.04 22 #7 7/8" (.8759) 2.044 40.88 Typical applications: Dams, atomic power stations 25 #8 1" (1.0009) 2.670 53.40 or commercial buildings 29 #9 1-1/8" (1.1289) 3.400 68.00 No-Grade 32 #10 1-1/4" (1.2709) 4.303 86.06 No-grade rebar is not tested as it is rolled. Cannot 36 #11 1-3/8" (1.4109) 5.313 106.26 be used in applications where mill certified products 43 #14 1-3/4" (1.6939) 7.650 153.00 are required. 57 #18 2-1/4" (2.2579) 13.600 272.00 Typical applications: Sidewalks, driveways, or Cut To Size Rebar other flat pours Cut to size rebar has a variety of applications. It can be ASTM Specifications used for concrete reinforcement, construction stakes, ASTM A 615 landscaping projects or tree and vegetable stakes. -

AASHTO GFRP-Reinforced Concrete Design Training Course
AASHTO GFRP-Reinforced Concrete Design Training Course GoToWebinar by: Professor Antonio Nanni Introducing the Schedule 9:35 am Introduction & Materials (Prof. Antonio Nanni) → Review Questions (Dr. Francisco De Caso) 10:30 am Flexure Response (Prof. Antonio Nanni) → Review Questions (Dr. Francisco De Caso) *** Coffee Break *** → Design Example: Flat Slab (Roberto Rodriguez) 12:00 pm Shear Response (Prof. Antonio Nanni) → Review Questions (Dr. Francisco De Caso) *** Lunch Break (1 hour) *** 1:30 pm → Design Example: Bent Cap (Nafiseh Kiani) 2:00 pm Axial Response (Prof. Antonio Nanni) → Review Questions (Dr. Francisco De Caso) → Design Example: Soldier Pile (Roberto Rodriguez) *** Coffee Break *** 3:00 pm Case Studies & Field Operations (Prof. Nanni & Steve Nolan) 1 Introducing our Presenters & Support Prof. Antonio Nanni Dr. Francisco DeCaso P.E. PhD. P.E. PhD. Roberto Rodriguez, Nafiseh Kiani P.E. (PhD. Candidate) (PhD. Candidate) Alvaro Ruiz, Christian Steputat, (PhD. Candidate) P.E. (PhD. Candidate) Steve Nolan, P2.E. Support Material - Handouts 3 Support Material - Handouts 4 Support Material - Handouts 5 Support Material - Handouts 6 Support Material - Workbook 7 Support Material - Workbook 8 Other Support Material - FDOT https://www.fdot.gov/structures/innovation/FRP.shtm 9 Another Training Opportunity CFRP-Prestressed Concrete Designer Training for Bridges & Structures – Professor Abdeldjelil “DJ” Belarbi, on September 9th, 2020 This 6-hour online training is focused on providing practical designer guidance to FDOT engineers and consultants for structures utilizing Carbon Fiber-Reinforced Polymer (CFRP) Strands for pretensioned bridge beams, bearing piles, and sheet piles. Basic design principles and design examples will be presented for typical FDOT bridge precast elements. Register Now at: https://attendee.gotowebinar.com/register/5898046861643311883 There is no cost to attend this webinar training. -

Interlocking Concrete Masonry Unit Geometry Design Raquel Avila Santa Clara Univeristy
Santa Clara University Scholar Commons Civil Engineering Senior Theses Engineering Senior Theses 6-13-2015 Interlocking concrete masonry unit geometry design Raquel Avila Santa Clara Univeristy Nick Jensen Santa Clara Univeristy Follow this and additional works at: https://scholarcommons.scu.edu/ceng_senior Part of the Civil and Environmental Engineering Commons Recommended Citation Avila, Raquel and Jensen, Nick, "Interlocking concrete masonry unit geometry design" (2015). Civil Engineering Senior Theses. 31. https://scholarcommons.scu.edu/ceng_senior/31 This Thesis is brought to you for free and open access by the Engineering Senior Theses at Scholar Commons. It has been accepted for inclusion in Civil Engineering Senior Theses by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. INTERLOCKING CONCRETE MASONRY UNIT GEOMETRY DESIGN By Raquel Avila, Nick Jensen SENIOR DESIGN PROJECT REPORT Submitted to the Department of Civil Engineering of SANTA CLARA UNIVERSITY in Partial Fulfillment of the Requirements for the degree of Bachelor of Science in Civil Engineering Santa Clara, California Spring 2015 Abstract Earthquakes in Haiti and Nepal left many people devastated. Millions of people were initially displaced and forced to reside in displacement camps. Developing countries like these need a form of economical construction. Our design and manufacturing process for interlocking CMU (concrete masonry unit) blocks can help build low-cost homes quickly and efficiently. Wall construction costs are reduced because skilled masons are not needed to build the wall. Instead, unskilled homeowners and laborers can stack the interlocking blocks, which serve as forms for the subsequent placement of reinforcement and grout within some of the CMU block voids. -

Stainless Steel Prestressing Strands and Bars for Use in Prestressed Concrete Girders and Slabs
Stainless Steel Prestressing Strands and Bars for Use in Prestressed Concrete Girders and Slabs Morgan State University The Pennsylvania State University University of Maryland University of Virginia Virginia Polytechnic Institute & State University West Virginia University The Pennsylvania State University The Thomas D. Larson Pennsylvania Transportation Institute Transportation Research Building University Park, PA 16802-4710 Phone: 814-865-1891 Fax: 814-863-3707 www.mautc.psu.edu MD-13-SP--SPMSU-3-11 Martin O’Malley, Governor James T. Smith, Secretary Anthony G. Brown, Lt. Governor Melinda B. Peters, Administrator STATE HIGHWAY ADMINISTRATION Research Report STAINLESS STEEL PRESTRESSING STRANDS AND BARS FOR USE IN PRESTRESSED CONCRETE GIRDERS AND SLABS MORGAN STATE UNIVERSITY DEPARTMENT OF CIVIL ENGINEERING PROJECT NUMBER SP309B4G FINAL REPORT FEBRUARY 2015 1. Report No. 2. Government Accession No. 3. Recipient’s Catalog No. MSU- 2013-02 4. Title and Subtitle 5. Report Date Stainless Steel Prestressing Strands and Bars for Use in February 2015 Prestressed Concrete Girders and Slabs 6. Performing Organization Code 7. Author(s) 8. Performing Organization Report No. Principal Investigator: Dr. Monique Head Researchers: Ebony Ashby-Bey, Kyle Edmonds, Steve Efe, Siafa Grose and Isaac Mason 9. Performing Organization Name and Address 10. Work Unit No. (TRAIS) Morgan State University Clarence M. Mitchell, Jr., School of Engineering Department of Civil Engineering 11. Contract or Grant No. 1700 E. Cold Spring Lane Baltimore, Maryland 21251 DTRT12-G-UTC03 12. Sponsoring Agency Name and Address 13. Type of Report and Period Covered US Department of Transportation Final Research & Innovative Technology Admin UTC Program, RDT-30 14. Sponsoring Agency Code 1200 New Jersey Ave., SE Washington, DC 20590 15. -

Concrete Terminology
DIVISION 3 - CAST IN PLACE CONCRETE TERMINOLOGY A. CONCRETE: A mixture of 1 part Portland Cement ( 22 lbs ) 2 Parts Dry Sand ( 41 lbs ) 3 Parts Dry Aggregate ( 70 lbs ) ½ Part Water ( 10 lbs ) Admixtures ( 7 lbs ) Total Weight Per Cu. Foot = 150 lbs. Area of 1 CU. FT. 1,728 cu. Inches 1. CAST IN PLACE CONCRETE: Concrete that is formed, poured and cured in it’s permanent position. 2. CURED CONCRETE: Concrete which has reached dehydration and obtained it’s maximum compressive strength. 3. GREEN CONCRETE: Concrete which remains hydrated and is in it’s earliest setting stage and has not hardened or cured appreciably. 4. LIGHTWEIGHT CONCRETE: A concrete mixture of substantially lower unit weight and compressive strength than that made from crushed stone or rock aggregate. Typically used on upper floors or roof tops where normal compressive strength is not a requirement and weight is a factor. 5. MONOLITHILIC CONCRETE: A single pour which includes the footing and slab concrete in a single pour . 6. POST-TENSION CONCRETE: A method of stressing reinforced concrete by which the tendons or cables are tightened after the concrete slab has hardened and in place. 24 7. PRE-CAST CONCRETE: Concrete which is cast and cured in a place other than it’s final resting position. ( Beams, Columns, Slabs, Lintels ) 8. PRE-STRESSED CONCRETE: A process of preparing concrete slabs and beams for extra strength by pouring concrete over tightly drawn steel cables, steel rods or tendons. 9. REINFORCED CONCRETE: Concrete with added materials such as steel rod, wire mesh, fiber mesh, dowel bars, expanded metal fabric, or cold drawn wire cable which act together with the concrete to resist cracking or movement B. -

Rebar Splicing Handbook Concrete Construction Products
BUILDING STRENGTH™ REBAR SPLICING HANDBOOK CONCRETE CONSTRUCTION PRODUCTS Table of Contents Information General and Technical Information ......................................................................1 and Technical General Safety Notes and Product Application ............................................................................................................................................1 Dayton Superior Technical Assistance ...........................................................................................................................................1 Table 1.1 Reinforcing Bar Data......................................................................................................................................................... 2 Table 1.2 Mechanical Requirements for Standard ASTM Deformed Reinforcing Bars ................................................................ 2 Table 1.3 Mechanical Splice ACI and ICC Code Requirements ...................................................................................................... 3 Table 1.4 Deformation Requirements for Standard ASTM Deformed Reinforcing Bars .............................................................. 3 Threaded Table 1.5 Chemical Composition Requirements for Standard ASTM Deformed Reinforcing Bars .............................................. 3 Splicing Systems Table 1.6 Grade 60 Rebar ............................................................................................................................................................... -

Unit Masonry
DIVISION 04 – MASONRY SECTION 04 20 00 – UNIT MASONRY SECTION 04 20 00 – UNIT MASONRY PART 1 – GENERAL 1.01 SUMMARY A. This Section includes unit masonry assemblies consisting of the following: 1. Concrete masonry units (CMUs). 2. Decorative concrete masonry units. 3. Concrete brick. 4. Mortar and grout. 5. Reinforcing steel. 6. Masonry joint reinforcement. 7. CMU Cell Flashing Pans. 8. Miscellaneous masonry accessories. 9. Masonry-cell insulation. B. Products installed, but not furnished, under this Section include the following: 1. Steel lintels and shelf angles for unit masonry, furnished under Division 05 Section 05 50 00 Metal Fabrications. 1.02 DEFINITIONS A. Reinforced Masonry: Masonry containing reinforcing steel in grouted cells. 1.03 PERFORMANCE REQUIREMENTS A. Provide structural unit masonry that develops indicated net-area compressive strengths (f'm) at 28 days. B. Determine net-area compressive strength (f'm) of masonry from average net-area compressive strengths of masonry units and mortar types (unit-strength method) according to Tables 1 and 2 in ACI 530.1/ASCE 6/TMS 602. Herbert, Rowland & Grubic, Inc. 04 20 00-1 000208.0489 DIVISION 04 – MASONRY SECTION 04 20 00 – UNIT MASONRY 1.04 SUBMITTALS A. Product Data: For each type of product indicated. B. Shop Drawings: For the following: 1. Reinforcing Steel: Detail bending and placement of unit masonry reinforcing bars. Comply with ACI 315, "Details and Detailing of Concrete Reinforcement.” Show elevations of reinforced walls. C. Samples for Verification: For each type and color of the following: 1. Exposed concrete masonry units. 2. Pigmented and colored-aggregate mortar. -

High Performance Concrete and Drilled Shaft Construction
High Performance Concrete and Drilled Shaft Construction Dr. Dan Brown, P.E. Dr. Anton Schindler Auburn University A Proposal for High Performance Concrete • Similar concept as used for current high performance concrete, but • Performance characteristics for fresh concrete properties (rather than hardened) 1 Why? Workability and Passing Ability tremie rebar concrete Concrete with inadequate Concrete with good workability workability and filling ability 2 Congested Rebar Cage Exposure of Trapped Laittance Attributed to Inadequate Workability 3 Congested Rebar Cage SCC Mix 4 Conventional Concrete Workability Retention Fresh, fluid concrete Trapped Laittance Old, stiff concrete 5 600 Tremie Placement Loading Traveling Hopper # 1 500 Waiting Period 12:05 AM: tremie stuck, rigging failure resulted 12:30 AM: tremie re-rigged, pulled free. 400 12:35 AM: tremie over-flowed , pour stopped, cable up and down. 12:40 AM: flow resumed, but last 10CY in hopper would not come out, sprayed and wasted. 300 1:00 AM: new hopper, flow resumed. 5 hrs 34 min. 200 Concrete Volume (CY) Volume Concrete 100 0 PM PM AM 10:00 11:00 12:00 6:00 PM 6:00 PM 7:00 PM 8:00 PM 9:00 AM 1:00 AM 2:00 AM 3:00 AM 4:00 AM 5:00 AM 6:00 AM 7:00 Unit Weight (kN / cu. m) Anomaly – Probable Defect of Unknown Size Mean Minus 3 Standard Depth (m) Deviations Possible Contaminated Mean Concrete at Base of Shaft Near One Tube 6 Bleeding Bleeding Crack 7 Bleeding Cracks Bleeding 8 Temperature 14 T0 = Initial Temperature T0 = 90° F τ = 28.0 hrs 12 β = 1.50 αu = 0.850 ) 3 10 T0 = 80° F 8 6 -

Rebar Strainmeters and “Sister Bars”
Model 4911, 4911A Rebar Strainmeters and “Sister Bars” Applications Rebar Strainmeters are com- monly used for measuring strains in… Concrete piles & caissons Slurry walls Cast-in-place concrete piles Concrete foundation slabs and footings Osterberg pile tests All concrete structures Model 4911A Rebar Strainmeter (front) and the Model 4911 “Sister Bar” (rear). Operating Principle Advantages and Limitations Rebar Strainmeters and “Sister Bars” are designed to The main advantage of the Rebar Strainmeters and “Sister be embedded in concrete for the purpose of measur- Bars” lies in their ruggedness. They are fully waterproof ing concrete strains due to imposed loads. The Rebar and virtually indestructible so that, if the cable is ade- Strainmeter is designed to be welded into, and become quately protected, they are safe from damage during the an integral part of, the existing rebar cage, while the concrete placement. “Sister Bar” is installed by tying it alongside an existing Each Rebar Strainmeter and “Sister Bar” is individu- length of rebar in the rebar cage. ally calibrated and tested for weld strength. The Rebar The rebar extensions on either side of the central strain- Strainmeter requires the services of an experienced gauged area are long enough to ensure adequate con- welder who can guarantee full-strength welds, whereas tact with the surrounding concrete so that the measured the “Sister Bar” is very easy to install. strains inside the steel are equal to the strains in the Close-up of Model 4911 shown as in- The single vibrating wire strain sensor, located along the surrounding concrete. stalled in concrete pile reinforcing cage. -

Severely Damaged Reinforced Concrete Circular Columns Repaired by Turned Steel Rebar and High-Performance Concrete Jacketing with Steel Or Polymer Fibers
Article Severely Damaged Reinforced Concrete Circular Columns Repaired by Turned Steel Rebar and High-Performance Concrete Jacketing with Steel or Polymer Fibers Junqing Xue 1, Davide Lavorato 2,*, Alessandro V. Bergami 2, Camillo Nuti 2, Bruno Briseghella 1, Giuseppe C. Marano 1, Tao Ji 1, Ivo Vanzi 3, Angelo M. Tarantino 4 and Silvia Santini 2 1 College of Civil Engineering, Fuzhou University, Fuzhou 350108, China; [email protected] (J.X.); [email protected] (B.B.); [email protected] (G.C.M.); [email protected] (T.J.) 2 Department of Architecture, Roma Tre University, 00153 Rome, Italy; [email protected] (A.V.B.); [email protected] (C.N.); [email protected] (S.S.) 3 Department of Engineering and Geology, University of Chieti and Pescara, 65127 Pescara, Italy; [email protected] 4 Department of Engineering, University of Modena and Reggio, 41125 Modena, Italy; [email protected] * Correspondence: [email protected] Received: 25 August 2018; Accepted: 10 September 2018; Published: 15 September 2018 Abstract: A new strategy that repairs severely damaged reinforced concrete (RC) columns after an earthquake is proposed as a simpler and quicker solution with respect to the strategies currently available in the literature. The external concrete parts are removed from the column surface along the whole plastic hinge region to uncover the steel reinforcement. The transverse steel is cut away, and each longitudinal rebar is locally substituted by steel rebar segments connected by welding connections to the original undamaged rebar pieces outside the intervention zone. The new rebar segments have a reduced diameter achieved by turning to ensure plastic deformation only in the plastic hinge, protecting the original rebar and the welding connections. -
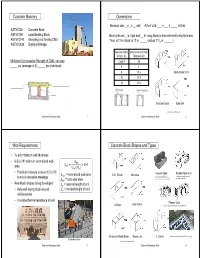
Concrete Masonry Dimensions Web Requirements Concrete Block
Concrete Masonry Dimensions Nominal size: _ x _ x __ unit Actual size: ___ x ___ x _____ inches ASTM C55 Concrete Brick ASTM C90 Load-Bearing Block Most units are _ in. high and __ in. long; block is then referred to by thickness. ASTM C140 Sampling and Testing CMU 5 Thus, a 12 in. block is 12 in. _____ (actual 11 /8 in. ______) ASTM C426 Drying shrinkage Nominal Width Minimum Face Shell of Unit (in) Thickness (in) Minimum Compressive Strength of CMU, net area 3 and 4 3/4 _____ psi (average of 3); _____ psi (individual) 61 81 1/4 Sash/Corner Unit 10 1 1/4 12 1 1/4 ____________ _________ ____ Stretcher Units Solid Unit http://www.oneontablock.com/ Concrete Masonry Units 1 Concrete Masonry Units 2 Web Requirements Concrete Block Shapes and Types • ¾ inch minimum web thickness 2 2 •6.5 in./ft minimum normalized web area 144 2 2 • Practical minimum is about 12 in. /ft Header Block Double Open End = normalized web area 135° Return Bullnose https://www.lowes.com/pd/Block-USA- http://www.rcpblock.com/block_ to avoid excessive breakage Header-Concrete-Block-Common-16-in-x-8- precision-shapes.html in-x-8-in-Actual-16-in-x-8-in-x-8-in/3599430 = total web area • New block shapes being developed = nominal length of unit • Help with laying block around = nominal height of unit reinforcement • Increase thermal resistance of wall Pilaster Units A Block Lintel Block http://www.rcpblock.com/block_precision-shapes.html Knock-out Bond Beam Rebar Unit L Corner https://www.youtube.com/watch?v=CECM474_uck theproblock.com http://www.oneontablock.com/