DOCSLIB.ORG

Engineering Formula Sheet

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Engineering Formula Sheet Engineering Formula Sheet Statistics Mode Place data in ascending order. Mean Mode = most frequently occurring value ∑ x If two values occur at the maximum frequency the data set is bimodal. If three or more values occur at the maximum µ = mean value frequency the data set is multi-modal. Σxi = sum of all data values (x1, x2, x3, … n = number of data values Median Place data in ascending order. Standard Deviation If n is odd, median = central value If n is even, median = mean of two central values ∑(x ) √ n = number of data values σ = standard deviation Range x = individual data value ( x , x , x , … i 1 2 3 Range = xmax - xmin n = number of data values xmax = maximum data value x = minimum data value min Probability Independent Events Frequency P (A and B and C) = PAPBPC x P (A and B and C) = probability of independent x events A and B and C occurring in sequence PA = probability of event A x x Mutually Exclusive Events fx = relative frequency of outcome x nx = number of events with outcome x P (A or B) = PA + PB n = total number of events P = probability of outcome x P (A or B) = probability of either mutually exclusive x event A or B occurring in a trial fa = frequency of all events PA = probability of event A Σxi = sum of all data values (x1, x2, x3, … Binomial Probability (order doesn’t matter) n = number of data values Conditional Probability ( ) ( | ) Pk = binomial probability of k successes in n trials ( | ) ( ) ( | ) ( ) ( | ) p = probability of a success q = 1 – p = probability of failure k = number of successes P (A|D) = probability of event A given event D P(A) = probability of event A occurring n = number of trials P(~A) = probability of event A not occurring P(D| ~A) = probability of event D given event A did not occur PLTW, Inc. Engineering Formulas IED POE DE CEA AE BE CIM EDD 1 Plane Geometry Ellipse Rectangle 2b Perimeter = 2a + 2b Circle 2a Area = ab B Triangle Parallelogram c Area = ½ bh a h h 2 2 2 a = b + c – 2bc·cos∠A Area = bh 2 2 2 A b = a + c – 2ac·cos∠B C b b c2 = a2 + b2 – 2ab·cos∠C s Right Triangle Regular Polygons f 2 2 2 c = a + b c a n = number of sides θ b Trapezoid a h Area = ½(a + b)h h h b Solid Geometry h Cube Sphere s Volume = s3 r Surface Area = 6s2 Volume r3 s s Surface Area = 4 r2 Rectangular Prism Cylinder h r Volume = wdh 2 h Surface Area = 2(wd + wh + dh) Volume = r h w d 2 Surface Area = 2 r h+2 r Right Circular Cone h Irregular Prism r h √ Volume = Ah A = area of base Pyramid h Constants A = area of base g = 9.8 m/s2 = 32.27 ft/s2 G = 6.67 x 10-11 m3/kg·s2 π = 3.14159 PLTW, Inc. Engineering Formulas IED POE DE CEA AE BE CIM EDD 2 Conversions Mass Area Force Energy 2 1 kg = 2.205 lbm 1 acre = 4047 m 1 N = 0.225 lbf 1 J = 0.239 cal 2 -4 1 slug = 32.2 lbm = 43,560 ft 1 kip = 1,000 lbf = 9.48 x 10 Btu 2 1 ton = 2000 lbm = 0.00156 mi = 0.7376 ft·lbf Pressure 1kW h = 3,6000,000 J Length Volume 1 atm = 1.01325 bar = 33.9 ft H2O 1 m = 3.28 ft 1L = 0.264 gal = 29.92 in. Hg Defined Units 1 km = 0.621 mi = 0.0353 ft3 = 760 mm Hg 1 in. = 2.54 cm = 33.8 fl oz = 101,325 Pa 1 mi = 5280 ft 1mL = 1 cm3 = 1 cc 1 J = 1 N·m = 14.7 psi 2 1 yd = 3 ft 1 N = 1 kg·m / s 1psi = 2.31 ft of H2O 1 Pa = 1 N / m2 Time 1 V = 1 W / A Temperature Change 1 d = 24 h Power 1 W = 1 J / s 1 K = 1 ºC 1 h = 60 min 1 W = 1 V / A 1 W = 3.412 Btu/h -1 1 min = 60 s 1 Hz = 1 s = 1.8 ºF = 0.00134 hp 1 yr = 365 d 1 F = 1 A·s / V = 1.8 ºR = 14.34 cal/min 1 H = 1 V·s / V = 0.7376 ft lb /s · f SI Prefixes Numbers Less Than One Numbers Greater Than One Power of 10 Prefix Abbreviation Power of 10 Prefix Abbreviation 10-1 deci- d 101 deca- da 10-2 centi- c 102 hecto- h 10-3 milli- m 103 kilo- k 10-6 micro- µ 106 Mega- M 10-9 nano- n 109 Giga- G 10-12 pico- p 1012 Tera- T 10-15 femto- f 1015 Peta- P 10-18 atto- a 1018 Exa- E 10-21 zepto- z 1021 Zetta- Z 10-24 yocto- y 1024 Yotta- Y Equations Temperature Force F = ma TK = TC + 273 Mass and Weight F = force TR = TF + 460 m = mass M = VDm a = acceleration W = mg W = VDw Equations of Static Equilibrium V = volume ΣFx = 0 ΣFy = 0 ΣMP = 0 TK = temperature in Kelvin Dm = mass density TC = temperature in Celsius m = mass Fx = force in the x-direction TR = temperature in Rankin Fy = force in the y-direction Dw = weight density TF = temperature in Fahrenheit g = acceleration due to gravity MP = moment about point P PLTW, Inc. Engineering Formulas IED POE DE CEA AE BE CIM EDD 3 Equations (Continued) Electricity Ohm’s Law Energy: Work Fluid Mechanics V = IR P = IV W = work RT (series) = R1 + R2+ ··· + Rn F = force ’ L d = distance (Guy-L ’ L Power Kirchhoff’s Current Law P V = P V B y ’ L 1 1 2 2 IT = I1 + I2 + ··· + In Q = Av or ∑ A v = A v Kirchhoff’s Voltage Law 1 1 2 2 VT = V1 + V2 + ··· + Vn or ∑ P = power E = energy W = work absolute pressure = gauge pressure V = voltage t = time + atmospheric pressure VT = total voltage τ = torque I = current P = absolute pressure rpm = revolutions per minute I = total current F = Force T R = resistance A = Area R = total resistance V = volume T Efficiency P = power T = absolute temperature Q = flow rate y v = flow velocity Thermodynamics ′ ∆T Pout = useful power output Mechanics Pin = total power input (where acceleration = 0) ∆ Energy: Potential (where acceleration = 0) L U = potential energy m =mass L g = acceleration due to gravity A v = A v h = height 1 1 2 2 v = v0 + at Energy: Kinetic d = d + v t + ½at2 P = rate of heat transfer 0 0 2 2 Q = thermal energy v = v0 + 2a(d – d0) A = Area of thermal conductivity τ = dFsinθ U = coefficient of heat conductivity K = kinetic energy (U-factor) m = mass s = speed ∆T = change in temperature v = velocity v = velocity a = acceleration R = resistance to heat flow ( R-value) Energy: Thermal X = range k = thermal conductivity t = time v = velocity d = distance Pnet = net power radiated g = acceleration due to gravity -8 = 5.6696 x 10 Q = thermal energy d = distance m = mass θ = angle e = emissivity constant c = specific heat τ = torque T1, T2 = temperature at time 1, time 2 ∆T = change in temperature F = force v = flow velocity PLTW, Inc. Engineering Formulas POE 4 DE 4 Section Properties Moment of Inertia Rectangle Centroid h x x x̅ and y̅ xx b Right Triangle Centroid x̅ and y̅ I = moment of inertia of a rectangular section xx about x-x axis Semi-circle Centroid Complex Shapes Centroid ∑ x ∑ y x̅ y̅ x̅ and y̅ ∑ ∑ x̅ x x̅ x y̅ y y̅ y x = x distance to centroid of shape i i y = y distance to centroid of shape i i A = Area of shape i i Structural Analysis Material Properties Beam Formulas Stress (axial) Reaction B L Moment (at point of load) x L Deflection x (at point of load) = stress L Reaction F = axial force B A = cross-sectional area L Moment x (at center) L Strain (axial) Deflection x (at center) Reaction B L Moment x (between loads) = strain Deflection ( L - ) (at center) x L0 = original length δ = change in length Reaction and B L L Moment (at Point of Load) x L ( )√ ( ) Modulus of Elasticity Deflection ( ) (at √ ) Deformation: Axial Truss Analysis ( L 2J = M + R E = modulus of elasticity δ = stress J = number of joints = strain δ = deformation M =number of members A = cross-sectional area F = axial force R = number of reaction forces F = axial force L0 = original length δ = deformation A = cross-sectional area E = modulus of elasticity PLTW, Inc. Engineering Formulas POE 5 AE 4 CEA 4 Simple Machines Inclined Plane Mechanical Advantage (MA) L y ( ) Wedge IMA = Ideal Mechanical Advantage AMA = Actual Mechanical Advantage L DE = Effort Distance DR = Resistance Distance FE = Effort Force FR = Resistance Force Lever Screw 1st IMA = Class Pitch = 2nd C = Circumference Class r = radius Pitch = distance between threads TPI = Threads Per Inch 3rd Class Compound Machines MA = (MA ) (MA ) (MA ) . TOTAL 1 2 3 Wheel and Axle Gears; Sprockets with Chains; and Pulleys with Belts Ratios Effort at Axle ( ) Compound Gears B Effort at Wheel GRTOTAL = ( ) ( ) GR = Gear Ratio in = Angular Velocity - driver Pulley Systems out = Angular Velocity - driven Nin = Number of Teeth - driver IMA = Total number of strands of a single string Nout = Number of Teeth - driven supporting the resistance din = Diameter - driver dout = Diameter - driven = Torque - driver IMA = in = Torque - driven out PLTW, Inc. Engineering Formulas POE 6 Structural Design Steel Beam Design: Shear Steel Beam Design: Moment Spread Footing Design qnet = qallowable - pfooting Vn = 0.6FyAw Mn = FyZx M = allowable bending moment Va = allowable shear strength a M = nominal moment strength Vn = nominal shear strength n q = net allowable soil Ω = 1.67 = factor of safety for net Ωv = 1.5 = factor of safety for shear b bearing pressure bending moment Fy = yield stress qallowable = total allowable soil Fy = yield stress Aw = area of web bearing pressure Zx = plastic section modulus about pfooting = soil bearing pressure neutral axis due to footing weight Storm Water Runoff tfooting = thickness of footing q = soil bearing pressure Rational Method Runoff Coefficients P = column load applied Storm Water Drainage Categorized by Surface A = area of footing Q = CfCiA Forested 0.059—0.2 Asphalt 0.7—0.95 Brick 0.7—0.85 Concrete 0.8—0.95 Q = peak storm water runoff rate (ft3/s) Shingle roof 0.75—0.95 Cf = runoff coefficient adjustment Lawns, well drained (sandy soil) factor Up to 2% slope 0.05—0.1 C = runoff coefficient 2% to 7% slope 0.10—0.15 i = rainfall intensity (in./h) Over 7% slope 0.15—0.2 A = drainage area (acres) Lawns, poor drainage (clay soil) Up to 2% slope 0.13—0.17 Runoff Coefficient 2% to 7% slope 0.18—0.22 Adjustment Factor Over 7% slope 0.25—0.35 Driveways,
Load more

Recommended publications
  • Simulation and Modeling of the Hydrodynamic, Thermal, and Structural Behavior of Foil Thrust Bearings
    Simulation and Modeling of the Hydrodynamic, Thermal, and Structural Behavior of Foil Thrust Bearings by Robert Jack Bruckner Submitted in partial fulfillment of the requirements For the degree of Doctor of Philosophy Dissertation Advisor: Dr. Joseph M. Prahl Department of Mechanical and Aerospace Engineering CASE WESTERN RESERVE UNIVERSITY August, 2004 Dedications All of the work leading to and included in these pages is dedicated to the loving support of my family, Lisa, Eric, and Elisabeth Table of Contents CHAPTER 1 Introduction to Foil Bearings .........................................................................................17 1.1 Historical Context of Hydrodynamics.............................................................17 1.2 Foil Bearing State of the Art...........................................................................19 1.3 Aviation Turbofan Engine Application...........................................................22 1.4 Typical Geometries and Characteristics of Foil Thrust Bearings.....................23 CHAPTER 2 Development of the Governing Equations......................................................................29 2.1 The Generalized Foil Bearing Problem...........................................................29 2.2 Reynolds Equation .........................................................................................29 2.2.1 Development from Mass and Momentum Conservation..............................29 2.2.3 Cylindrical (Thrust Pad) Form of Reynolds Equation .................................40
    [Show full text]
  • Study on Mechanical Bearing Strength and Failure Modes of Composite Materials for Marine Structures
    Journal of Marine Science and Engineering Article Study on Mechanical Bearing Strength and Failure Modes of Composite Materials for Marine Structures Dong-Uk Kim 1 , Hyoung-Seock Seo 1,* and Ho-Yun Jang 2 1 School of Naval Architecture & Ocean Engineering, University of Ulsan, Ulsan 44610, Korea; [email protected] 2 Green Ship Research Division, Research Institute of Medium & Small Shipbuilding, Busan 46757, Korea; [email protected] * Correspondence: [email protected] Abstract: With the gradual application of composite materials to ships and offshore structures, the structural strength of composites that can replace steel should be explored. In this study, the mechanical bearing strength and failure modes of a composite-to-metal joining structure connected by mechanically fastened joints were experimentally analyzed. The effects of the fiber tensile strength and stress concentration on the static bearing strength and failure modes of the composite structures ◦ ◦ ◦ ◦ were investigated. For the experiment, quasi-isotropic [45 /0 /–45 /90 ]2S carbon fiber-reinforced plastic (CFRP) and glass fiber-reinforced plastic (GFRP) specimens were prepared with hole diameters of 5, 6, 8, and 10 mm. The experimental results showed that the average static bearing strength of the CFRP specimen was 30% or higher than that of the GFRP specimen. In terms of the failure mode of the mechanically fastened joint, a cleavage failure mode was observed in the GFRP specimen for hole diameters of 5 mm and 6 mm, whereas a net-tension failure mode was observed for hole diameters of 8 mm and 10 mm. Bearing failure occurred in the CFRP specimens.
    [Show full text]
  • Chapter 5 Footing Design
    Chapter 5 Footing Design By S. Ali Mirza1 and William Brant2 5.1 Introduction Reinforced concrete foundations, or footings, transmit loads from a structure to the supporting soil. Footings are designed based on the nature of the loading, the properties of the footing and the properties of the soil. Design of a footing typically consists of the following steps: 1. Determine the requirements for the footing, including the loading and the nature of the supported structure. 2. Select options for the footing and determine the necessary soils parameters. This step is often completed by consulting with a Geotechnical Engineer. 3. The geometry of the foundation is selected so that any minimum requirements based on soils parameters are met. Following are typical requirements: • The calculated bearing pressures need to be less than the allowable bearing pressures. Bearing pressures are the pressures that the footing exerts on the supporting soil. Bearing pressures are measured in units of force per unit area, such as pounds per square foot. • The calculated settlement of the footing, due to applied loads, needs to be less than the allowable settlement. • The footing needs to have sufficient capacity to resist sliding caused by any horizontal loads. • The footing needs to be sufficiently stable to resist overturning loads. Overturning loads are commonly caused by horizontal loads applied above the base of the footing. • Local conditions. • Building code requirements. 1 Professor Emeritus of Civil Engineering, Lakehead University, Thunder Bay, ON, Canada. 2 Structural Engineer, Black & Veatch, Kansas City, KS. 1 4. Structural design of the footing is completed, including selection and spacing of reinforcing steel in accordance with ACI 318 and any applicable building code.
    [Show full text]
  • Design for Hydrostatic Bearing of Vertical Type Pump
    Transactions of the Korean Nuclear Society Autumn Meeting Gyeongju, Korea, October 29-30, 2015 Design for Hydrostatic Bearing of Vertical Type Pump Kang Soo Kim a, Sung Kyun Kim a, Gyeong Hoi Koo a, Keun Bae Park a aKorea Atomic Energy Research Institute, 989-111 Daedeok-daero, Yuseong-gu, Daejeon *Corresponding author: [email protected] 1. Introduction of sodium(η) at 100 ℃ and 400 ℃ are 0.682 cp, 0.278 cp respectively[2]. 0.278 cp = 0.000278 Pa.s = 0.278×10-9 kg. The primary pump of PGSFR(Prototype Gen IV Sodium sec/mm2. Fast Reactor) performs an important safety function of circulating the coolant across the core to remove the nuclear heat under all operating conditions of the reactor. Design and selection of materials and manufacturing technology for sodium pumps differ to a large extent from conventional pumps because these pumps operate relatively at high temperatures and have high reliability. The configuration of the primary pump of PGSFR is shown in Figure 1. In order to provide guide to the shaft at the bottom part, there is a hydrostatic bearing above the impeller level. In this paper, the FEM(Finite Element Method) analysis was performed to evaluate the unbalance force for the rotary shaft for the design of the hydrostatic bearing and the design methodology and procedures for the hydrostatic bearing are established. Figure 2 FEM model for the unbalance force 2.1 Bearing Pressure Calculation The sodium flow way due to the pressure difference is shown in Figure 3. The sodium discharged from the impellor flows through the diffuser and then, the small part of sodium flows from the diffuser oriffice to the hydrostatic bearing due to the pressure difference.
    [Show full text]
  • Performance of Hydrodynamic Journal Bearing Under the Combined Influence of Textured Surface and Journal Misalignment
    Performance of hydrodynamic journal bearing under the combined influence of textured surface and journal misalignment: A numerical survey Belkacem Manser, Idir Belaidi, Abderrachid Hamrani, Sofiane Khelladi, Farid Bakir To cite this version: Belkacem Manser, Idir Belaidi, Abderrachid Hamrani, Sofiane Khelladi, Farid Bakir. Performance of hydrodynamic journal bearing under the combined influence of textured surface and journal misalign- ment: A numerical survey. Comptes Rendus Mécanique, Elsevier Masson, 2019, 347 (2), pp.141-165. 10.1016/j.crme.2018.11.002. hal-02438009 HAL Id: hal-02438009 https://hal.archives-ouvertes.fr/hal-02438009 Submitted on 14 Jan 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Performance of hydrodynamic journal bearing under the combined influence of textured surface and journal misalignment: a numerical survey B. MANSER1;∗; I. BELAIDI1; A. HAMRANI1; S. KHELLADI2 & F. BAKIR2 1 LEMI., FSI., University of M’hamed Bougara, Avenue de I’independance,´ 35000-Boumerdes, Algeria. 2 DynFluid Lab., Arts et Metiers´ ParisTech, 151 boulevard de l’Hopital,ˆ 75013-Paris, France. ∗ Corresponding author : [email protected] Abstract A wisely chosen geometry of micro textures with the favorable relative motion of lubricated surfaces in contacts can enhance tribological characteristics, in this paper, a computational investigation related to the combined influence of bearing surface texturing and journal misalignment on the performances of hydrodynamic journal bearings is reported.
    [Show full text]
  • A Numerical and Experimental Investigation of Taylor Flow Instabilities in Narrow Gaps and Their Relationship to Turbulent Flow
    A NUMERICAL AND EXPERIMENTAL INVESTIGATION OF TAYLOR FLOW INSTABILITIES IN NARROW GAPS AND THEIR RELATIONSHIP TO TURBULENT FLOW IN BEARINGS A Dissertation Presented to The Graduate Faculty of The University of Akron In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Dingfeng Deng August, 2007 A NUMERICAL AND EXPERIMENTAL INVESTIGATION OF TAYLOR FLOW INSTABILITIES IN NARROW GAPS AND THEIR RELATIONSHIP TO TURBULENT FLOW IN BEARINGS Dingfeng Deng Dissertation Approved: Accepted: _______________________________ _______________________________ Advisor Department Chair Dr. M. J. Braun Dr. C. Batur _______________________________ _______________________________ Committee Member Dean of the College Dr. J. Drummond Dr. G. K. Haritos _______________________________ _______________________________ Committee Member Dean of the Graduate School Dr. S. I. Hariharan Dr. G. R. Newkome _______________________________ _______________________________ Committee Member Date R. C. Hendricks _______________________________ Committee Member Dr. A. Povitsky _______________________________ Committee Member Dr. G. Young ii ABSTRACT The relationship between the onset of Taylor instability and appearance of what is commonly known as “turbulence” in narrow gaps between two cylinders is investigated. A question open to debate is whether the flow formations observed during Taylor instability regimes are, or are related to the actual “turbulence” as it is presently modeled in micro-scale clearance flows. This question is approached by considering the viscous fluid flow in narrow gaps between two cylinders with various eccentricity ratios. The computational engine is provided by CFD-ACE+, a commercial multi-physics software. The flow patterns, velocity profiles and torques on the outer cylinder are determined when the speed of the inner cylinder, clearance and eccentricity ratio are changed on a parametric basis.
    [Show full text]
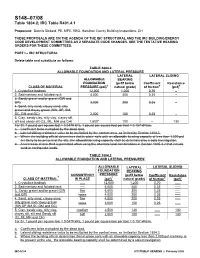
  • S148–07/08 Table 1804.2; IRC Table R401.4.1
    S148–07/08 Table 1804.2; IRC Table R401.4.1 Proponent: Dennis Dickard, PE, MPE, RBO, Hamilton County Building Inspections, OH THESE PROPOSALS ARE ON THE AGENDA OF THE IBC STRUCTURAL AND THE IRC BUILDING/ENERGY CODE DEVELOPMENT COMMITTEES AS 2 SEPARATE CODE CHANGES. SEE THE TENTATIVE HEARING ORDERS FOR THESE COMMITTEES. PART I – IBC STRUCTURAL Delete table and substitute as follows: TABLE 1804.2 ALLOWABLE FOUNDATION AND LATERAL PRESSURE LATERAL LATERAL SLIDING ALLOWABLE BEARING FOUNDATION (psf/f below Coefficient Resistance CLASS OF MATERIAL PRESSURE (psf)d natural grade) of frictiona (psf)b 1. Crystalline bedrock 12,000 1,200 0.70 – 2. Sedimentary and foliated rock 4,000 400 0.35 – 3. Sandy gravel and/or gravel (GW and GP) 3,000 200 0.35 – 4. Sand, silty sand, clayey sand, silty gravel and clayey gravel (SW, SP, SM, SC, GM and GC) 2,000 150 0.25 – 5. Clay, sandy clay, silty clay, clayey silt, silt and sandy silt (CL, ML, MH and CH) 1,500c 100 -- 130 For SI: 1 pound per square foot = 0.0479 kPa, 1 pound per square foot per foot = 0.157 kPa/m. a. Coefficient to be multiplied by the dead load. b. Lateral sliding resistance value to be multiplied by the contact area, as limited by Section 1804.3. c. Where the building official determines that in-place soils with an allowable bearing capacity of less than 1,500 psf are likely to be present at the site, the allowablebearing capacity shall be determined by a soils investigation. d. An increase of one-third is permitted when using the alternate load combinations in Section 1605.3.2 that include wind or earthquake loads.
    [Show full text]
  • Report R807 (PDF, 501.14KB)
    The University of Sydney Department of Civil Engineering Sydney NSW 2006 AUSTRALIA http://www.civil.usyd.edu.au Centre for Geotechnical Research Research Report No. R807 DEEP PENETRATION OF STRIP AND CIRCULAR FOOTINGS INTO LAYERED CLAYS By Changxin Wang, BE, ME John P. Carter, BE, PhD, FIEAust, MASCE May 2001 DEEP PENETRATION OF STRIP AND CIRCULAR FOOTINGS INTO LAYERED CLAYS Research Report No R807 Changxin Wang, BE, ME John P.Carter, BE, PhD, FIEAust, MASCE The University of Sydney Department of Civil Engineering Centre for Geotechnical Research http://www.civil.usyd.edu.au ABSTRACT The bearing behaviour of footings on layered soils has received significant attention from researchers, but most of the reported studies are limited to footings resting on the surface of the soil and are based on the assumption of small deformations. In this paper, large deformation analyses, simulating the penetration of strip and circular footings into two-layered clays, are described. The upper layer was assumed to be stronger than the lower layer. The importance of large deformation analysis for this problem is illustrated by comparing the small and large deformation predictions. The bearing behaviour is discussed and the undrained bearing capacity factors are given for various cases involving different layer thicknesses and different ratios of the undrained shear strengths of the two clay layers. The development of the plastic zones and the effect of soil self-weight on the bearing capacity are also discussed in the report. Keywords: large deformation, penetration, strip footing, circular footing, layered clays, bearing capacity Deep Penetration of Strip and Circular Footings Into Layered Clays May, 2001 Copyright Notice Department of Civil Engineering, Research Report R807 Deep penetration of strip and circular footings into layered clays © 2001 C.X.
    [Show full text]
  • Numerical Simulation of Internal Self-Controlled Restrictor Hydrostatic Bearing with Discrete Oil Pocket Area SONG Yanming, YANG
    Advances in Engineering Research, volume 121 2nd International Conference on Advances in Materials, Mechatronics and Civil Engineering (ICAMMCE 2017) Numerical Simulation of Internal Self-Controlled Restrictor Hydrostatic Bearing with Discrete Oil Pocket Area SONG Yanming, YANG Yang, ZHAO Gang School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China Key words: numerical simulation, pressure field, velocity filed, self-controlled restrictor hydrostatic bearing, discrete oil pocket area Abstract: The computational fluid dynamics (CFD) method was used to establish the model of internal self-controlled restrictor hydrostatic bearing with discrete oil pocket area. The pressure field and velocity filed were calculated with different supply pressures and eccentricity ratios by the numerical simulation. The simulation results indicate that the load capacity of film increases with the supply pressure growing. The pressure in the lower oil pocket is larger than that in upper one. The flow also increases with supply pressure growing, but little relationship with the eccentricity. The bearing at the diameter of 200mm is designed and manufactured. The operation tests demonstrate that the pressure and velocity plot in the pocket is similar to the simulation one. 1 Introduction Internal self-controlled restrictor hydrostatic bearing is placed in a fluid form bearing support within the bearing body, using the throttle gap with the outer surface of the spindle surface formed in the body of the fluid medium is throttled(Guo,2007). Because of the variable throttle ratio, making the self-controlled hydrostatic bearing has a large load capacity and high film rigidity. The simple restrictor hydrostatic bearing is increasingly used in high-precision machine tools and processing equipment(Yoshimoto,1993).
    [Show full text]
  • Geotechnical Engineering Circular No. 6 6
    Technical Report Documentation Page 1. Report No. 2. Government Accession No. 3. Recipient’s Catalog No. FHWA-SA-02-054 4. Title and Subtitle 5. Report Date September 2002 GEOTECHNICAL ENGINEERING CIRCULAR NO. 6 6. Performing Organization Code Shallow Foundations 7. Author(s) 8. Performing Organization Report No. Robert E. Kimmerling 9. Performing Organization Name and Address 10. Work Unit No. (TRAIS) PanGEO, Inc. th 3414 N.E. 55 Street 11. Contract or Grant No. Seattle, Washington 98105 DTFH61-00-C-00031 12. Sponsoring Agency Name and Address 13. Type of Report and Period Covered Office of Bridge Technology Technical Manual Federal Highway Administration 14. Sponsoring Agency Code HIBT, Room 3203 400 Seventh Street, S.W. Washington, D.C. 20590 15. Supplementary Notes Contracting Officer’s Technical Representative: Chien-Tan Chang (HIBT) FHWA Technical Consultant: Jerry DiMaggio (HIBT) 16. Abstract This document is FHWA’s primary reference of recommended design and procurement procedures for shallow foundations. The Circular presents state-of-the-practice guidance on the design of shallow foundation support of highway bridges. The information is intended to be practical in nature, and to especially encourage the cost-effective use of shallow foundations bearing on structural fills. To the greatest extent possible, the document coalesces the research, development and application of shallow foundation support for transportation structures over the last several decades. Detailed design examples are provided for shallow foundations in several bridge support applications according to both Service Load Design (Appendix B) and Load and Resistance Factor Design (Appendix C) methodologies. Guidance is also provided for shallow foundation applications for minor structures and buildings associated with transportation projects.
    [Show full text]
  • PRESSURE DISTRIBUTION and FRICTION COEFFICIENT of HYDRODYNAMIC JOURNAL BEARING 1Mr.Akash S
    PRESSURE DISTRIBUTION AND FRICTION COEFFICIENT OF HYDRODYNAMIC JOURNAL BEARING 1Mr.Akash S. Patil, 2Mr.Kaustubh S. Zambre, 3 4 Mr.Pramod R. Mali, Prof.N.D.Patil 1,2,3 B.E. Mechanical Dept. P.V.P.I.T, Budhgaon, (India) 4 Assistant Professor, Mechanical Dept. P.V.P.I.T, Budhgaon, (India) ABSTRACT The research approach of this paper is.A journal bearing supports the load in radial direction and which is working on hydrodynamic lubrication.Lubricated journal bearings present a common challenge for construction equipment manufacturers in the world. The common design methodology is based on actual data and has worked very well historically because the industries and governments have accepted that bearings in construction equipment need frequent lubrication and exchange of worn parts. These requirements call for better methods of designing lubricated journal bearings.The aim of the carried work is to develop data for better design methods for lubricated journal bearing design used in heavy duty construction equipment machines, in order to prolong life and lubrication intervals. Keywords: Friction coefficient, Hydrodynamic Lubrication, Journal bearings, Pressuregeneration, Sliding Surfaces I INTRODUCTION During the past fewyears hydrodynamic journal bearings have got great attention from analytical and practical engineers. Due to wide range of engineering application such as pumps, compressors, turbines, nuclear reactors, precision machine tools, the growth of journal bearing technology increases in considerable amount. Fluid film lubrication is hydrodynamic phenomenon characterized by a lubricant flowing in narrow gap between closely spaced surfaces; it avoids solid to solid contact and thus reduces friction and wear in significant amount which results in increases component life.
    [Show full text]
  • A Refined Formula for the Allowable Bearing Pressure in Soils and Rocks Using Shear Wave Velocities
    Earthquake–Soil Interaction 233 A refined formula for the allowable bearing pressure in soils and rocks using shear wave velocities S. S. Tezcan & Z. Ozdemir Bogazici University, Istanbul, Turkey Abstract Based on a variety of case histories of site investigations, including extensive bore hole data, laboratory testing and geophysical prospecting at more than 550 construction sites, an empirical formulation is proposed for the rapid determination of allowable bearing pressure of shallow foundations in soils and rocks. The proposed expression is corroborated consistently by the results of the classical theory and its application is proven to be rapid and reliable. Plate load tests have been also carried out at three different sites, in order to further confirm the validity of the proposed method. The latter incorporates only two soil parameters, namely, the in situ measured shear wave velocity and the unit weight. The unit weight may also be determined with sufficient accuracy by means of other proposed empirical expressions, using P or S-wave velocities. It is indicated that once the shear and P-wave velocities are measured in situ by an appropriate geophysical survey, the allowable bearing pressure as well as the coefficient of subgrade reaction and many other elasticity parameters may be determined rapidly and reliably. Keywords: shear wave velocity, shallow foundations, allowable bearing pressure, dynamic technique, soils and rocks. 1 Introduction Professor Schulze [1], a prominent historical figure in soil mechanics and foundation
    [Show full text]