Clonal Selection from First Principles
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ch. 43 the Immune System
Ch. 43 The Immune System 1 Essential Questions: How does our immunity arise? How does our immune system work? 2 Overview of immunity: Two kinds of defense: A. innate immunity present at time of birth before exposed to pathogens nonspecific responses, broad in range skin and mucous membranes internal cellular and chemical defenses that get through skin macrophages, phagocytic cells B. acquired immunity (adaptive immunity)develops after exposure to specific microbes, abnormal body cells, foreign substances or toxins highly specific lymphocytes produce antibodies or directly destroy cells 3 Overview of Immune System nonspecific Specific 4 I. Innate immunity Nonspecific defenses A. First line of defense: skin, mucous membranes skin protects against chemical, mechanical, pathogenic, UV light damage mucous membranes line digestive, respiratory, and genitourinary tracts prevent pathogens by trapping in mucus *breaks in skin or mucous membranes = entryway for pathogen 5 secretions of skin also protect against microbes sebaceous and sweat glands keep pH at 35 stomach also secretes HCl (Hepatitis A virus can get past this) produce antimicrobial proteins (lysozyme) ex. in tears http://vrc.belfastinstitute.ac.uk/resources/skin/skin.htm 6 B. Second line of defense internal cellular and chemical defenses (still nonspecific) phagocytes produce antimicrobial proteins and initiate inflammation (helps limit spread of microbes) bind to receptor sites on microbe, then engulfs microbe, which fused with lysosome nitric oxide and poisons in lysosome can poison microbe lysozyme and other enzymes degrade the microbe *some bacteria have capsule that prevents attachment *some bacteria are resistant to lysozyme macrophages 7 Cellular Innate defenses Tolllike receptor (TLR) recognize fragments of molecules characteristic of a set of pathogens [Ex. -

The RAG Recombinase Dictates Functional Heterogeneity and Cellular Fitness in Natural Killer Cells
The RAG Recombinase Dictates Functional Heterogeneity and Cellular Fitness in Natural Killer Cells Jenny M. Karo,1 David G. Schatz,2 and Joseph C. Sun1,* 1Immunology Program and Gerstner Sloan Kettering Graduate School of Biomedical Sciences, Memorial Sloan Kettering Cancer Center, New York, NY 10065, USA 2Department of Immunobiology and the Howard Hughes Medical Institute, Yale University School of Medicine, New Haven, CT 06510, USA *Correspondence: [email protected] http://dx.doi.org/10.1016/j.cell.2014.08.026 SUMMARY completely absent (Mombaerts et al., 1992; Shinkai et al., 1992). There is as yet no evidence that RAG plays a physiological The emergence of recombination-activating genes role in any cell type other than B and T lymphocytes or in any pro- (RAGs) in jawed vertebrates endowed adaptive cess other than V(D)J recombination. immune cells with the ability to assemble a diverse Although NK cells have long been classified as a component set of antigen receptor genes. In contrast, innate of the innate immune system, recent evidence suggests that lymphocytes, such as natural killer (NK) cells, are this cell type possesses traits attributable to adaptive immunity not believed to require RAGs. Here, we report that (Sun and Lanier, 2011). These characteristics include ‘‘educa- tion’’ mechanisms to ensure self-tolerance during NK cell devel- NK cells unable to express RAGs or RAG endonu- opment and clonal-like expansion of antigen-specific NK clease activity during ontogeny exhibit a cell-intrinsic cells during viral infection, followed by the ability to generate hyperresponsiveness but a diminished capacity long-lived ‘‘memory’’ NK cells. -

LECTURE 05 Acquired Immunity and Clonal Selection
LECTURE: 05 Title: ACQUIRED "ADAPTIVE" IMMUNITY & CLONAL SELECTION THEROY LEARNING OBJECTIVES: The student should be able to: • Recognize that, acquired or adaptive immunity is a specific immunity. • Explain the mechanism of development of the specific immunity. • Enumerate the components of the specific immunity such as A. Primary immune response. B. Secondary immune response • Explain the different phases that are included in the primary and secondary immune responses such as: A. The induction phase. B. Exponential phase. C. Steady phase. D. Decline phase. • Compare between the phases of the primary and secondary immune responses. • Determine the type of the immunoglobulins involved in each phase. • Determine which immunoglobulin is induced first and, that last longer. • Enumerate the characteristics of the specific immunity such as: A. The ability to distinguish self from non-self. B. Specificity. C. Immunological memory. • Explain naturally and artificially acquired immunity (passive, and active). • Explain the two interrelated and independent mechanisms of the specific immune response such as : A. Humoral immunity. B. Cell-mediated (cellular) immunity. • Recognize that, the specific immunity is not always protective, for example; sometimes it causes allergies (hay fever), or it may be directed against one of the body’s own constituents, resulting in autoimmunity (thyroditis). LECTURE REFRENCE: 1. TEXTBOOK: ROITT, BROSTOFF, MALE IMMUNOLOGY. 6th edition. Chapter 2. pp. 15-31 2. TEXTBOOK: ABUL K. ABBAS. ANDREW H. LICHTMAN. CELLULAR AND MOLECULAR IMMUNOLOGY. 5TH EDITION. Chapter 1. pg 3-12. 1 ACQUIRED (SPECIFIC) IMMUNITY INTRODUCTION Adaptive immunity is created after an interaction of lymphocytes with particular foreign substances which are recognized specifically by those lymphocytes. -

Med-Pathway Zoom Workshop
MCAT Immunology Dr. Phillip Carpenter medpathwaymcat Med-pathway AAMC MCAT Content Outline: Immunology Category 1A: Structure/Function of Proteins/AA Immune System Category 3B: Organ Systems Innate vs. Adaptive Immunity T and B Lymphocytes Macrophages & Phagocytes Tissue-Bone marrow, Spleen, Thymus, Lymph nodes Antigen and Antibody Antigen Presentation Clonal Selection Antigen-Antibody recognition Structure of antibody molecule Self vs. Non-self, Autoimmune Diseases Major Histocompatibility Complex Lab Techniques: ELISA & Western Blotting Hematopoiesis Creates Immune Cells Self vs. Non-self Innate vs Adaptive Innate Immunity Physical Barriers: Skin, mucous membranes, pH Inflammatory mediators: Complement, Cytokines, Prostaglandins Cellular Components: Phagocytes-Neutrophils, Eosinophils, Basophils, Mast Cells Antigen Presenting Cells-Monocytes, Macrophages, Dendritic Cells Adaptive (Acquired) Immunity Composed of B and T lymphocytes: Activated by Innate Immunity B cells: Express B cell receptor and secrete antibodies as plasma cells T cells: Mature in thymus, express TCR surface receptor; Activated by Antigen Presenting Cells (APCs) Direct Immune response (The Ringleaders of immune system) Major Lymphoid Organs TYPE SITE FUNCTION Fetal production of Liver 1° lymphoid cells Hematopoietic production of 1° Bone marrow myeloid and lymphoid cells Receives bone marrow T 1° Thymus cells; site where self is selected from non-self Lymph nodes 2° Sites of antigen activation Spleen of lymphocytes; clearance Macrophages (Sentinel Cells) Pattern Recognition -

Theories of Antibodies Production
THEORIES OF ANTIBODIES PRODUCTION 1. Instructive Theories a. Direct Template Theory b. Indirect Template Theory 2. Selective Theories a. Natural Selection Theory b. Side Chain Theory c. Clonal Selection Theory d. Immune Network Theory INSTRUCTIVE THEORIES Instructive theories suggest that an immunocompetent cell is capable of synthesizing antibodies of all specificity. The antigen directs the immunocompetent cell to produce complementary antibodies. According to these theories the antigen play a central role in determining the specificity of antibody molecule. Two instructive theories are postulated as follows: Direct template theory: This theory was first postulated by Breinl and Haurowitz (1930). They suggested that a particular antigen or antigenic determinants would serve as a template against which antibodies would fold. The antibody molecule would thereby assume a configuration complementary to antigen template. This theory was further advanced as Direct Template Theory by Linus Pauling in 1940s. Indirect template theory: This theory was first postulated by Burnet and Fenner (1949). They suggested that the entry of antigenic determinants into the antibody producing cells induced a heritable change in these cells. A genocopy of the antigenic determinant was incorporated in genome of these cells and transmitted to the progeny cells. However, this theory that tried to explain specificity and secondary responses is no longer accepted. SELECTIVE THEORIES Selective theories suggest that it is not antigen, but the antibody molecule that play a central role in determining its specificity. The immune system already possess pre-formed antibodies of different specificities prior to encounter with an antigen. Three selective theories were postulated as follows: Side chain theory: This theory was proposed by Ehrlich (1898). -

A Series of Adaptive Models Inspired by the Acquired Immune System
A Series of Adaptive Models Inspired by the Acquired Immune System JASON BROWNLEE Technical Report 070227A Complex Intelligent Systems Laboratory, Centre for Information Technology Research, Faculty of Information Communication Technology, Swinburne University of Technology Melbourne, Australia [email protected] Abstract-The acquired immune system is capable of the presented series of adaptive models as a novel specialising a defence of an organism in response to the its hierarchal framework for which existing and future antigenic environment. This complex biological system possess acquired immunity inspired adaptive models may be interesting information processing features such as learning, interpreted and related. memory, and the ability to generalize. The clonal selection theory is a cornerstone of modern biology in understanding the acquired II. PRINCIPLE COMPONENTS immune system from the perspective of B-lymphocyte cells and This section lists a series of principles (operators or antibody diversity. This work presents a series of computational mechanisms) that are sufficiently low in complexity to adaptive systems inspired by features of the biological immune be analysed independently. It is expected that the system and the clonal selection theory in particular. Starting with mechanisms listed in this section may act as component basic clonal operators as principle components, models are features in larger adaptive models. Operators are presented in increasing complexity from canonical clonal assigned a notation of O# and -

A Network Model for Clonal Differentiation and Immune Memory
ARTICLE IN PRESS Physica A 355 (2005) 408–426 www.elsevier.com/locate/physa A network model for clonal differentiation and immune memory Alexandre de Castroa,b,Ã aCentro Regional VI, Universidade Estadual do Rio Grande do Sul 90010-030, Porto Alegre, RS, Brazil bInstituto de Fı´sica, Universidade Federal do Rio Grande do Sul 91501-970, Porto Alegre, RS, Brazil Received 21 June 2004 Available online 17 May 2005 Abstract A model of bit-strings, that uses the technique of multi-spin coding, was previously used to study the time evolution of B-cell clone repertoire, in a paper by Lagreca, Almeida and Santos. In this work we extend that simplified model to include independently the role of the populations of antibodies, in the control of the immune response, producing mechanisms of differentiation and regulation in a more complete way. Although the antibodies have the same molecular shape of the B-cells receptors (BCR), they should present a different time evolution and thus should be treated separately. We have also studied a possible model for the network immune memory, suggesting a random memory regeneration, which is self-perpetuating. r 2005 Elsevier B.V. All rights reserved. Keywords: Immune memory; Antibodies evolution; Memory regenerating 1. Introduction In the last decades, due in part to the spread of the world AIDS epidemy, the scientific community started to dedicate special attention to the immunological system, responsible for the defense of the organism against microscopic invaders. ÃCorresponding author. Centro Regional VI, Universidade Estadual do Rio Grande do Sul 90010-030, Porto Alegre, RS, Brazil. -

Interplay of Natural Killer Cells and Their Receptors with the Adaptive Immune Response
REVIEW BRIDGING INNATE AND ADAPTIVE IMMUNITY Interplay of natural killer cells and their receptors with the adaptive immune response David H Raulet Although natural killer (NK) cells are defined as a component of the innate immune system, they exhibit certain features generally considered characteristic of the adaptive immune system. NK cells also participate directly in adaptive immune responses, mainly by interacting with dendritic cells. Such interactions can positively or negatively regulate dendritic cell activity. Reciprocally, dendritic cells regulate NK cell function. In addition, ‘NK receptors’ are frequently expressed by T cells and can directly regulate the functions of these cells. In these distinct ways, NK cells and their receptors influence the adaptive http://www.nature.com/natureimmunology immune response. Natural killer (NK) cells, a component of the innate immune system, Themes of NK cell recognition mediate cellular cytotoxicity and produce chemokines and inflamma- The recognition strategies used by NK cells are diverse. These include tory cytokines such as interferon-γ (IFN-γ) and tumor necrosis factor recognition of pathogen-encoded molecules; recognition of self pro- (TNF), among other activities1. They are important in attacking teins whose expression is upregulated in transformed or infected cells pathogen-infected cells, especially during the early phases of an infec- (‘induced-self recognition’); and inhibitory recognition of self pro- tion1,2. They are also efficient killers of tumor cells and are believed to be teins that are expressed by normal cells but downregulated by infected involved in tumor surveillance. The long-standing hypothesis that NK or transformed cells (‘missing-self recognition’). What follows are cells exert an immunoregulatory effect is supported by recent evidence examples of each. -
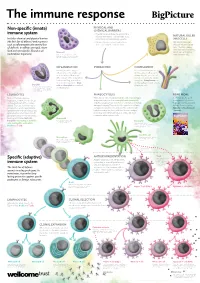
Non-Specific (Innate) Immune System Specific (Adaptive) Immune System
The immune response PHYSICAL AND Non-specific (innate) CHEMICAL BARRIERS immune system • Physical barriers include the skin and the mucous membranes of the airways, guts, NATURAL KILLER Includes chemical and physical barriers and urinary and reproductive systems. (NK) CELLS (the first line of defence) and responses • Chemical barriers include hydrochloric NK cells kill pathogen- such as inflammation (the second line acid secreted by the stomach lining. infected cells and cancer of defence). Its effects are rapid, short- cells. They also release chemicals called cytokines, lived and non-specific. Found in all Mast cell which alert and attract multicellular organisms. Cells involved in allergic responses, releasing other immune cells. histamine and other inflammatory molecules. Mast cells sit within skin and mucosal tissues. INFLAMMATION IF BREACHED COMPLEMENT Invading microbes trigger A set of around 30 proteins in inflammation. This involves an the blood plasma that can be increase in blood flow to the activated by the presence of affected part of the body, which microbes or antibody–antigen leads to swelling, pain and an complexes. Complement can increase in temperature. Mast destroy pathogens and activate Basophil cells and basophils are involved phagocytic cells. Cells involved in allergic and inflammatory responses. Basophils release histamine in inflammation. like mast cells, but unlike mast cells they circulate in the blood. LEUKOCYTES PHAGOCYTOSIS READ MORE Made in the bone marrow, White blood cells including dendritic cells, macrophages Big Picture is a free post- leukocytes, or white blood cells, are and granulocytes such as eosinophils and neutrophils 16 magazine for teachers an important part of the immune engulf (or phagocytose) microbes or cells that are infected, that explores issues around system. -

Proliferation of Antibody in Clonal Selection Algorithm with Immunological Memory Cell
SCIS & ISIS 2010, Dec. 8-12, 2010, Okayama Convention Center, Okayama, Japan Proliferation of Antibody in Clonal Selection Algorithm with Immunological Memory Cell Takumi Ichimura Takashi Yamaguchi & Kenneth James Mackin Faculty of Management and Information Systems, Faculty of Informatics, Prefectural University of Hiroshima Tokyo University of Information Sciences 1-1-71, Ujina-Higashi, Minami-ku, 4-1 Onaridai, Wakaba-ku, Chiba, 265-8501 Japan Hiroshima, 734-8559, Japan Email: ftyamagu, [email protected] Email: [email protected] Abstract—The clonal selection principle explains the basic Experimental results for classification of the medical database features of an adaptive immune response to a antigenic stimulus. will be reported in Section 5. In Section 6, we give some It established the idea that only those cells that recognize the discussions to conclude this paper. antigens are selected to proliferate and differentiate. This paper explains a computational implementation of the clonal selection II. THE CLONAL SELECTION THEORY principle that explicitly takes into account the affinity maturation of the immune response. The clonal selection algorithm in this Burnet proposed the clonal selection theory in order to paper finds the antigen by the 3 kinds of combination types of explain the essential features of adaptive immune response Immunological Memory cells and the proliferation of immune [13][14]. The basic idea of this theory interprets the response cells. This paper tried to classify the medical database of Heart Disease database in the the UCI Repository. of lymphocytes in the face of an antigenic stimulus. Any molecule that can be recognized by the adaptive I. -

A Review of the Clonal Selection Theory of Acquired Immunity
A Review of the Clonal Selection Theory of Acquired Immunity JASON BROWNLEE Technical Report 070223A Complex Intelligent Systems Laboratory, Centre for Information Technology Research, Faculty of Information Communication Technology, Swinburne University of Technology Melbourne, Australia [email protected] Abstract-The clonal selection theory proposed by Nobel Prize II. CLONAL SELECTION THEORY ¢ £ winning immunologist Frank Macfarlane Burnet is a deceptively £ simple algorithmic process that describes the diversity of Don t let conflicting and awkward facts stand in the antibodies and is the foundation for the understanding of the way of an esthetically satisfying theory whose fundamentals are consistent with the world model and ¢ acquired immune system of vertebrates. This paper provides a £ with one another! And be suspicious of facts that seem summary overview of the theory including its inception, main ¤ processes, and some interesting theoretical aspects. in the way of any coherent theory. Lederberg [21], pg 181. Keywords- Clonal Selection Theory, Clonal Selection Principle, Clonal Selection Algorithms, Artificial Immune System A.Theory Development Ada and Nossal [39] provide a detailed summary of I. INTRODUCTION the theories development and related confirmatory Cziko [19] on clonal selection theory: experiments, as does Silverstein [5]. See Forsdyke [9] for an account on the development of the theory [ ¡ ] the immune system does not attempt to predict ¦ the antibody structure that will bind with an antigen, but highlightin¥ g the contributions of Ehrlich. See [20] for ¢ £ Lederberg s comment on clonal selection and elective rather uses a type of shotgun approach that sends in a ¥ diverse army to meet the invaders ¤ theories , and [21] for his account on his part in the history of the developm ent of the theory. -

Antigens & Antibodies II Polyclonal Antibodies Vs Monoclonal Antibodies
A Brief Review of Antibody Structure A Brief Review of Antibody Structure Primary structure Tertiary structure The basic antibody is a dimer of dimer (2 heavy chain-light chain pairs) composed of repeats of a single structural unit known as the “immunoglobulin Secondary structure domain” Quaternary structure Antigens & Antibodies II Polyclonal antibodies vs Monoclonal antibodies Definitions A comparison of antigen recognition by B and T cells Polyclonal antibodies: antibody preparations from Factors that influence immunogenicity immunized animals. Consist of complex mixtures of different antibodies produced by many different B cell Quantitating the strength of antibody-antigen interactions clones Equilibrium constants equilibrium dialysis Monoclonal Antibody: homogeneous antibody preparations impact of multivalency produced in the laboratory. Consist of a single type of antigen binding site, produced by a single B cell clone Cross-reactivity of antibodies (later we’ll talk about how these are made). Measuring antibody-antigen binding Affinity between two macromolecules can measured using a biosensor Technique: Surface Plasmon Resonance Instrument: Biocore -Resonance units are proportional to the degree of binding of soluble ligand to the immobilized receptor. (or soluble antibody to immobilized antigen, as shown here) - Determining the amount of binding at equilibrium with different known concentrations of receptor (antibody) and ligand (protein antigen) allows you to calculate equilibrium constants (Ka, Kd). -Rate of dissociation and association (koff, kon) can also be calculated. 1 Avidity (strength of binding) is influenced by both Affinity refers to strength of binding of single Affinity (Ka of single binding site) x Valence of epitope to single antigen binding site. interaction (number of interacting binding sites) But antibodies have 2 or more identical binding sites.