Module 6: Two Dimensional Problems in Polar Coordinate System
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
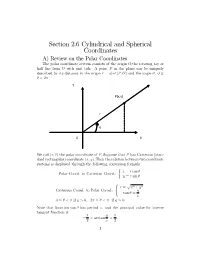
Section 2.6 Cylindrical and Spherical Coordinates
Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord. -

Designing Patterns with Polar Equations Using Maple
Designing Patterns with Polar Equations using Maple Somasundaram Velummylum Claflin University Department of Mathematics and Computer Science 400 Magnolia St Orangeburg, South Carolina 29115 U.S.A [email protected] The Cartesian coordinates and polar coordinates can be used to identify a point in two dimensions. The polar coordinate system has a fixed point O called the origin or pole and a directed half –line called the polar axis with end point O. A point P on the plane can be described by the polar coordinates ( r, θ ), where r is the radial distance from the origin and θ is the angle made by OP with the polar axis. Several important types of graphs have equations that are simpler in polar form than in rectangular form. For example, the polar equation of a circle having radius a and centered at the origin is simply r = a. In other words , polar coordinate system is useful in describing two dimensional regions that may be difficult to describe using Cartesian coordinates. For example, graphing the circle x 2 + y 2 = a 2 in Cartesian coordinates requires two functions, one for the upper half and one for the lower half. In polar coordinate system, the same circle has the very simple representation r = a. Maple can be used to create patterns in two dimensions using polar coordinate system. When we try to analyze two dimensional patterns mathematically it will be helpful if we can draw a set of patterns in different colors using the help of technology. To investigate and compare some patterns we will go through some examples of cardioids and rose curves that are drawn using Maple. -

Polar Coordinates and Calculus.Wxp
Polar Coordinates and Calculus Recall that in the Polar coordinate system the coordinates ) represent <ß the directed distance from the pole to the point and the directed angle, counterclockwise from the polar axis to the segment from the pole to the point. A polar function would be of the form: ) . < œ 0 To find the slope of the tangent line of a polar graph we will parameterize the equation. ) ( Assume is a differentiable function of ) ) <œ0 0 ¾Bœ<cos))) œ0 cos and Cœ< sin ))) œ0 sin . .C .C .) Recall also that œ .B .B .) 1Þ Find the derivative of < œ # sin ) Remember that horizontal tangent lines occur when and that vertical tangent lines occur when page 1 2 Find the HTL and VTL for cos ) and sketch the graph. Þ < œ # " page 2 Recall our formula for the derivative of a function in polar coordinates. Since Bœ<cos))) œ0 cos and Cœ< sin ))) œ0 sin , we can conclude .C .C .) that œ.B œ .B .) Solutions obtained by setting < œ ! gives equations of tangent lines through the pole. 3Þ Find the equations of the tangent line(s) through the pole if <œ#sin #Þ) page 3 To find the arc length of a polar curve, you have two options. 1) You can use the parametrization of the polar curve: cos))) cos and sin ))) sin Bœ< œ0 Cœ< œ0 then use the arc length formula for parametric curves: " w # w # 'α ÈÐBÐ) ÑÑ ÐCÐ ) ÑÑ . ) or, 2) You can use an alternative formula for arc length in polar form: " <# Ð.< Ñ # . -

Classical Mechanics Lecture Notes POLAR COORDINATES
PHYS 419: Classical Mechanics Lecture Notes POLAR COORDINATES A vector in two dimensions can be written in Cartesian coordinates as r = xx^ + yy^ (1) where x^ and y^ are unit vectors in the direction of Cartesian axes and x and y are the components of the vector, see also the ¯gure. It is often convenient to use coordinate systems other than the Cartesian system, in particular we will often use polar coordinates. These coordinates are speci¯ed by r = jrj and the angle Á between r and x^, see the ¯gure. The relations between the polar and Cartesian coordinates are very simple: x = r cos Á y = r sin Á and p y r = x2 + y2 Á = arctan : x The unit vectors of polar coordinate system are denoted by r^ and Á^. The former one is de¯ned accordingly as r r^ = (2) r Since r = r cos Á x^ + r sin Á y^; r^ = cos Á x^ + sin Á y^: The simplest way to de¯ne Á^ is to require it to be orthogonal to r^, i.e., to have r^ ¢ Á^ = 0. This gives the condition cos ÁÁx + sin ÁÁy = 0: 1 The simplest solution is Áx = ¡ sin Á and Áy = cos Á or a solution with signs reversed. This gives Á^ = ¡ sin Á x^ + cos Á y^: This vector has unit length Á^ ¢ Á^ = sin2 Á + cos2 Á = 1: The unit vectors are marked on the ¯gure. With our choice of sign, Á^ points in the direc- tion of increasing angle Á. Notice that r^ and Á^ are drawn from the position of the point considered. -

Section 6.7 Polar Coordinates 113
Section 6.7 Polar Coordinates 113 Course Number Section 6.7 Polar Coordinates Instructor Objective: In this lesson you learned how to plot points in the polar coordinate system and write equations in polar form. Date I. Introduction (Pages 476-477) What you should learn How to plot points in the To form the polar coordinate system in the plane, fix a point O, polar coordinate system called the pole or origin , and construct from O an initial ray called the polar axis . Then each point P in the plane can be assigned polar coordinates as follows: 1) r = directed distance from O to P 2) q = directed angle, counterclockwise from polar axis to the segment from O to P In the polar coordinate system, points do not have a unique representation. For instance, the point (r, q) can be represented as (r, q ± 2np) or (- r, q ± (2n + 1)p) , where n is any integer. Moreover, the pole is represented by (0, q), where q is any angle . Example 1: Plot the point (r, q) = (- 2, 11p/4) on the polar py/2 coordinate system. p x0 3p/2 Example 2: Find another polar representation of the point (4, p/6). Answers will vary. One such point is (- 4, 7p/6). Larson/Hostetler Trigonometry, Sixth Edition Student Success Organizer IAE Copyright © Houghton Mifflin Company. All rights reserved. 114 Chapter 6 Topics in Analytic Geometry II. Coordinate Conversion (Pages 477-478) What you should learn How to convert points The polar coordinates (r, q) are related to the rectangular from rectangular to polar coordinates (x, y) as follows . -

1.7 Cylindrical and Spherical Coordinates
56 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE 1.7 Cylindrical and Spherical Coordinates 1.7.1 Review: Polar Coordinates The polar coordinate system is a two-dimensional coordinate system in which the position of each point on the plane is determined by an angle and a distance. The distance is usually denoted r and the angle is usually denoted . Thus, in this coordinate system, the position of a point will be given by the ordered pair (r, ). These are called the polar coordinates These two quantities r and , are determined as follows. First, we need some reference points. You may recall that in the Cartesian coordinate system, everything was measured with respect to the coordinate axes. In the polar coordinate system, everything is measured with respect a fixed point called the pole and an axis called the polar axis. The is the equivalent of the origin in the Cartesian coordinate system. The polar axis corresponds to the positive x-axis. Given a point P in the plane, we draw a line from the pole to P . The distance from the pole to P is r, the angle, measured counterclockwise, by which the polar axis has to be rotated in order to go through P is . The polar coordinates of P are then (r, ). Figure 1.7.1 shows two points and their representation in the polar coordinate system. Remark 79 Let us make several remarks. 1. Recall that a positive value of means that we are moving counterclock- wise. But can also be negative. A negative value of means that the polar axis is rotated clockwise to intersect with P . -

Section Summary: Polar Coordinates A. Definitions B. Theorems C
Section Summary: Polar Coordinates a. Definitions The polar coordinate system (introduced by Newton) is an alter- native to the Cartesian coordinate system (named after Descartes) in which every point in the plane is expressed by its distance and direction (angle) from the origin, called the pole. The polar axis plays the role formerly played by the positive x-axis. The polar coordinates are often given as (r, θ), where r is the distance from the pole, and • θ is the angle between the polar axis and the ray passing through • the point of interest. The graph of a polar equation contains all points P that have at least one polar representation (r, θ) whose coordinates solve the equa- tion. b. Theorems None to speak of. c. Properties/Tricks/Hints/Etc. Given r and θ it’s easy to find the corresponding x and y: x = r cos θ y = r sin θ It’s not quite so easy to go in the opposite direction, unless we restrict r and θ: r [0, ) ∈ ∞ θ [0, 2π) ∈ gives a unique representation in polar coordinates (except for the pole, which has equation r = 0 regardless of the value of θ). 1 As a convenience we let r take negative values: so ( r, θ)=(r, θ + π) − In any event, we see that, by contrast with the Cartesian coordinate system, the polar coordinate system allows points to have multiple representations. To find the Cartesian coordinates from the polar coordinates, we can use the equations r = √x2 + y2 −1 y θ = tan x Be careful, however, as there are two values of θ that solve these equa- tions in each interval of 2π, and one must choose the proper value based on the quadrant in which (x, y) lies... -

The Polar Coordinate System
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 The Polar Coordinate System Alisa Favinger University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Favinger, Alisa, "The Polar Coordinate System" (2008). MAT Exam Expository Papers. 12. https://digitalcommons.unl.edu/mathmidexppap/12 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. The Polar Coordinate System Alisa Favinger Cozad, Nebraska In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 Polar Coordinate System ~ 1 Representing a position in a two-dimensional plane can be done several ways. It is taught early in Algebra how to represent a point in the Cartesian (or rectangular) plane. In this plane a point is represented by the coordinates (x, y), where x tells the horizontal distance from the origin and y the vertical distance. The polar coordinate system is an alternative to this rectangular system. In this system, instead of a point being represented by (x, y) coordinates, a point is represented by (r, θ) where r represents the length of a straight line from the point to the origin and θ represents the angle that straight line makes with the horizontal axis. -

Graphing and Converting Polar and Rectangular Coordinates Butterflies Are Among the Most Celebrated of All Insects
Using Polar Coordinates Graphing and converting polar and rectangular coordinates Butterflies are among the most celebrated of all insects. It’s hard not to notice their beautiful colors and graceful flight. Their symmetry can be explored with trigonometric functions and a system for plotting points called the polar coordinate system. In many cases, polar coordinates are simpler and easier to use than rectangular coordinates. We are going to look at a You are familiar with new coordinate system plotting with a rectangular called the polar coordinate system. coordinate system. The center of the graph is Angles are measured from called the pole. the positive x axis. Points are represented by a radiusradius and an angle (r, ) To plot the point 5, 4 First find the angle Then move out along the terminal side 5 The polar coordinate system is formed by fixing a point, O, which is the pole (or origin). The polar axis is the ray constructed from O. Each point P in the plane can be assigned polar coordinates (r, ). P = (r, ) O = directed angle Polar Pole (Origin) axis r is the directed distance from O to P. is the directed angle (counterclockwise) from the polar axis to OP. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5 Graphing Polar Coordinates The grid at the left is a polar grid. The A typical angles of 30o, 45o, 90o, … are shown on the graph along with circles of radius 1, 2, 3, 4, and 5 units. Points in polar form are given as (r, ) where r is the radius to the point and is the angle of the point. -

Section 8.3 Polar Form of Complex Numbers 527
Section 8.3 Polar Form of Complex Numbers 527 Section 8.3 Polar Form of Complex Numbers From previous classes, you may have encountered “imaginary numbers” – the square roots of negative numbers – and, more generally, complex numbers which are the sum of a real number and an imaginary number. While these are useful for expressing the solutions to quadratic equations, they have much richer applications in electrical engineering, signal analysis, and other fields. Most of these more advanced applications rely on properties that arise from looking at complex numbers from the perspective of polar coordinates. We will begin with a review of the definition of complex numbers. Imaginary Number i The most basic complex number is i, defined to be i = −1 , commonly called an imaginary number . Any real multiple of i is also an imaginary number. Example 1 Simplify − 9 . We can separate − 9 as 9 −1. We can take the square root of 9, and write the square root of -1 as i. − 9 = 9 −1 = 3i A complex number is the sum of a real number and an imaginary number. Complex Number A complex number is a number z = a + bi , where a and b are real numbers a is the real part of the complex number b is the imaginary part of the complex number i = −1 Plotting a complex number We can plot real numbers on a number line. For example, if we wanted to show the number 3, we plot a point: 528 Chapter 8 imaginary To plot a complex number like 3 − 4i , we need more than just a number line since there are two components to the number. -

Charts and Manifolds – Tuesday, 27Th January 2015
Problem Set Four – Charts and Manifolds – Tuesday, 27th January 2015 Question 1 As an example of definition of manifolds, we shall look at the two dimensional sphere S2. Embedded in 3D Euclidean space (x1; x2; x3), coordinates on S2 are S2 = f(x1; x2; x3) 2 R3j(x1)2 + (x2)2 + (x3)2 = 1g: (1) ± We then define six hemispherical subsets Ui (i = 1; 2; 3) of the sphere: ± 1 2 3 2 i Ui = f(x ; x ; x ) 2 S j ± x > 0g: (2) We want to show that these six sets are “sewn smoothly.” To do so, we introduce charts ± ± 2 + 1 2 3 1 2 φi : Ui ! R as φ3 (x ; x ; x ) = (x ; x ), etc. Write down explicitly maps like + + −1 1 φ1 ◦ (φ3 ) , and show that these are indeed C . Question 2 µ µ Given two vector fields X = X @µ and Y = Y @µ, we define their commutator (or Lie bracket) [X; Y ] by its action on a function f(xµ): [X; Y ](f) ≡ X(Y (f)) − Y (X(f)): (3) We shall show that [X; Y ] is a vector field. 1. If f and g are functions and a and b are real numbers, show that the commutator is linear: [X; Y ](af + bg) = a[X; Y ](f) + b[X; Y ](g): (4) 2. Show that it obeys the Leibniz rule, [X; Y ](fg) = f[X; Y ](g) + g[X; Y ](f): (5) This quantity is a ‘directional derivative’ of Y in the direction of the vector X. When suitably generalised, it can be used to find constants of the motion. -

Lecture 36: Polar Coordinates a Polar Coordinate System, Gives the Co-Ordinates of a Point with Reference to a Point O and a Half Line Or Ray Starting at the Point O
Lecture 36: Polar Coordinates A polar coordinate system, gives the co-ordinates of a point with reference to a point O and a half line or ray starting at the point O. We will look at polar coordinates for points in the xy-plane, using the origin (0; 0) and the positive x-axis for reference. A point P in the plane, has polar coordinates (r; θ), where r is the distance of the point from the origin and θ is the angle that the ray jOP j makes with the positive x-axis. Example 1 Plot the points whose polar coordinates are given by π π 7π 5π (2; ) (3; − ) (3; ) (2; ) 4 4 4 2 Note the representation of a point in polar coordinates is not unique. For instance for any θ the point (0; θ) represents the pole O. We extend the meaning of polar coordinate to the case when r is negative by agreeing that the two points (r; θ) and (−r; θ) are in the same line through O and at the same distance jrj but on opposite side of O. Thus (−r; θ) = (r; θ + π) 3π Example 2 Plot the point (−3; 4 ) 1 Polar to Cartesian coordinates To convert from Polar to Cartesian coordinates, we use the identities: x = r cos θ; y = r sin θ π π Example 3 Convert the following to Cartesian coordinates (2; 4 ) and (3; − 3 ) Cartesian to Polar coordinates To convert from Cartesian to polar coordinates, we use the following identities y r2 = x2 + y2; tan θ = x When choosing the value of θ, we must be careful to consider which quadrant the point is in, since for any given number a, there are two angles with tan θ = a, in the interval 0 ≤ θ ≤ 2π.