DOCSLIB.ORG

Doris and the Mass of Jupiter

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Doris and the Mass of Jupiter 2 N AT IONAL A E RO N A UT I CS AN D SPACE ADM I N ISTRAT IO N Technical Report 32-7382 The Motion of (48) Doris and the Mass of Jupiter J. William Zielenbach JET PROPULSION LABORATORY CALIFORNIA INSTITUTE OF TECHNOLOGY PASADENA, CALIFORNIA April 15, 1970 NATIONAL AERONAUTICS AND SPACE ADMINISTRATION Technical Report 32-7382 The Motion of (48) Doris and the Mass of Jupiter J. William Zielenbach JET PROPULSION LABORATORY CALIFORNIA INSTITUTE OF TECHNOLOGY PASADENA, CALIFORNIA April 15, 1970 Prepared Under Contract No. NAS 7-1 00 National Aeronautics and Space Administration Preface The work described in this report was performed by the Mission Analysis Division of the Jet Propulsion Laboratory. JPL TECHNICAL REPORT 32-1382 iii The major portion of this work was completed while the author was a student in Washington, D.C. However, much of the final computation and critical analysis was performed in the Mission Analysis Division at JPL. The author wishes to acknowledge the assistance of Raynor L. Duncombe of the United States Naval Observatory (USNO) and Douglas A. OHandley of JPL, who directed the research. Paul M. Janiczek of the USNO and Jay H. Lieske and J. Derral Mulholland of JPL contributed much advice and constructive criticism. Paul Herget of the Cincinnati Observatory made available the observation files of the Minor Planet Center. Francis J. Heyden, S.J., provided the facilities of the Georgetown College Observatory. Computing support came from the staff members and facilities of Georgetown University, the USNO, and JPL. Finally, the author appreciates the effort of those who responded to requests for positions remeasured from old plates: Th. Weimer, Algiers; G. v. Herk, Leiden; J. Dommanget, Uccle; A. Rohrmann, Heidelberg; R. Carrasco, Madrid; J. A. Bruwer, Johannesburg; H. Hirose, Tokyo; Y. Vaisala, Turku; C. Cristescu, Bucharest; L. Galkin, Crimean Astrophysical Observatory, H. J. M. Abraham, Mt. Stromlo; J. Fhbrer, Barcelona; H. L. Giclas, Lowell; Betty Mintz, USNO; and the Goethe Link Observatory. iv 32-I382 8 ntroduction ................ 1 II . Numerical Integration ............. 2 A . Equations To Be Integrated ........... 2 B . Method of Integration ............ 4 111 . Numerical Integration (Details of Application) ....... 6 1V . Least-Squares Differential orrection ......... 9 A . Conditional Equations ....... .... 9 B . Formation and Solution of Normal Equations ...... 9 V . Differentias Correcfion Coefficients ..........11 bservations ............14 A . Observed Angles ..............14 B . Observation Time .............16 C. Observatory Location ............17 VI1 . Discussion of bservations ............17 A . Collection and Selection ............17 B . Distribution ...............19 C. Weighting .............. 19 D . Residual Analysis . ............19 E . Catalog Corrections .............24 VIII . Discussion of Final Results .... ..... 24 Appendix A . Modifications to Newcomb's Theory of the Sun .....30 Appendix B . Eckert-Brouwer Differential Correction Coefficients ...31 Appendix C . Observations and Residuals .......34 References ........ 48 1. Physical constants ..... ....... 9 2 . Reciprocal solar masses ............ 9 3 . Observatories ............... 18 ~~1~~6REPORT 32-7382 Contents (contd 1 Tables (contd) 4 . Analysis of residuals by observatory and type ......23 5 . Comparison of published and rereduced observations ....24 6 . Definitive elements for (48) Doris based on the system of masses in Table 1 ...........27 7. Correlations in the solution for Keplerian elements .....29 8 . Normal matrices for solutions with ar/% and variational equations, and with &/am and Eckert-Brouwer set 3 .............29 A.1 . Replacements in Newcomb's theory of the sun ......30 B.1 . Eckert-Brouwer set 1 .............32 B.2 . Eckert-Brouwer set 2 .............32 8.3 . Eckert-Brouwer set 3 .............33 Figures 1 . Comparison of a predictor-only run with a predictor-corrector run. both of eighth order and 4-day stepsize ...... 7 2 . Effect of stepsize-predictor-corrector run at 8 days. minus one at 4 days ........... 8 3 . Right-ascension residuals for reference orbit .......20 4 . Distribution of observations ...........21 5 . Equatorial x and y coordinates of earth and (48) Doris at observation times ..........22 6 . Numerically integrated partial derivatives ax/ax, .....25 7 . Finite difference Ax/Ax,- numerically integrated ax/ax. .................26 8 . Declination residuals for reference orbit ........28 vi JPL TECHNICAL REPORT 32-7382 Abstract A definitive orbit is obtained for (48) Doris based upon the provisional reciprocal mass of Jupiter. Numerically integrated variational equations for the coordinates of Doris with respect to its initial rectangular coordinates and velocities and the mass of Jupiter are used to differentially correct the orbit of Doris and the mass of Jupiter. The reciprocal mass obtained, using 617 observations over a 110-yr time span, is 1047.340 20.016. JPL TECHNICAL REPORT 32- 1382 vii he Motion of (4 oris and the Mass of Jupiter 1. Introduction planets. Moreover, the general location of the belt of asteroids between Mars and Jupiter makes the asteroids Jupiter is the most massive planet in the solar system highly susceptible to Jovian perturbations. The para- and has an important gravitational influence on the motion graphs that follow indicate the reasons why certain of all other bodies in the solar system. Since the gravi- asteroids are more suitable than others for determining tational effect is dependent upon the mass of Jupiter, the mass of Jupiter by classical astronomical methods. this mass must be determined for accurate representation of planetary and interplanetary motions. From the theory of general perturbations (Ref. 2, p. 467), it is known that the disturbing function 9 for any object The mass of the planet itself is not easily determined perturbed by a body of mass m’ is given by from the motion of its satellites because the size and shape of the disk make it difficult to measure their posi- tions with respect to the center of the planet. The 9 = k2 interaction of the inner satellites is quite complicated, and relatively few observations have been made of the cos (in + kw + mM + yn’ + k’w’ + m’M’) outer, less perturbed satellites. Consequently, investi- gators have tended to analyze the gravitational effect of where a, e, i, 0, 0, and M are the usual Keplerian ele- the whole Jupiter system at interplanetary distances. ments for the perturbed body and the primed quantities are the elements of the perturbing planet. The analytical Newcomb (Ref. 1) pointed out that perhaps the best expressions for the time variations of the elements of the determination of the mass by classical astronomical perturbed body are obtained by integration. Since methods would be that afforded by the motion of minor the mean anomaly M can be written as planets (asteroids) because their positions can be more precisely observed than can those of comets or major M=nt+n 1 where n is the mean motion and t is the time elapsed results are critically analyzed, and the various compu- since M equaled U, the trigonometric term can be written tational aspects of the problem are discussed with the benefit of hindsight and with an eye to future research. cos [(in + j'n')t + e(i,j',k,k',m,m',s2,sz',","',o,d)l which, when integrated, will have a term involving II. Numerical integration (in + Yn') in the denominator. If there is a near com- Numerical solution of differential equations has be- mensurability of the mean motions n and n' for indices come common with the advent of electronic computers. i and j', the resulting coefficient of the theory is large and This is especially true for cases of perturbed motion for the period of the trigonometric term is long. which no complete analytical formulation is available. A typical example is the calculation of planetary orbits by In 1873, G. W. Hill (Ref. 3) drew attention to the fact the method of special perturbations. This section begins that the Hecuba group of minor planets has nearly 2:l with a description of the basic differential equation of commensurabilities of mean motions with Jupiter. This motion to be integrated, along with its partial derivatives gives rise to periodic perturbations of large amplitudes, with respect to various parameters. It concludes with a whose periods are short enough to be observed within brief description of the techniques used in the integration a reasonable length of time. He pointed out that, since and a presentation of general starting conditions. proximity to Jupiter greatly affects the magnitude of the perturbations, asteroids with large semimajor axes, as The equation of motion and its derivatives have been well as highly elliptic orbits whose aphelia are near expressed in a center-of-mass (c.m.) frame because the Jupiter, would be most desirable (as long as the mutual amount of computation required to evaluate E' for one inclination of the two orbits is small). These criteria are object perturbed by n planets and the sun is roughly fulfilled to a greater or lesser degree by the 13 minor (n + 1)/(2n + 1) of that required in heliocentric co- planets he recommended for future observation and ordinates. Transforming any quantity from barycentric analysis. to heliocentric merely involves subtracting the appro- priate barycentric value for the sun. Depending upon the Minor planet (48) Doris is one of this group. Its long number of equations being integrated and the bodies to period term is about 72 yr, and there has
Load more

Recommended publications
  • ESO's VLT Sphere and DAMIT
    ESO’s VLT Sphere and DAMIT ESO’s VLT SPHERE (using adaptive optics) and Joseph Durech (DAMIT) have a program to observe asteroids and collect light curve data to develop rotating 3D models with respect to time. Up till now, due to the limitations of modelling software, only convex profiles were produced. The aim is to reconstruct reliable nonconvex models of about 40 asteroids. Below is a list of targets that will be observed by SPHERE, for which detailed nonconvex shapes will be constructed. Special request by Joseph Durech: “If some of these asteroids have in next let's say two years some favourable occultations, it would be nice to combine the occultation chords with AO and light curves to improve the models.” 2 Pallas, 7 Iris, 8 Flora, 10 Hygiea, 11 Parthenope, 13 Egeria, 15 Eunomia, 16 Psyche, 18 Melpomene, 19 Fortuna, 20 Massalia, 22 Kalliope, 24 Themis, 29 Amphitrite, 31 Euphrosyne, 40 Harmonia, 41 Daphne, 51 Nemausa, 52 Europa, 59 Elpis, 65 Cybele, 87 Sylvia, 88 Thisbe, 89 Julia, 96 Aegle, 105 Artemis, 128 Nemesis, 145 Adeona, 187 Lamberta, 211 Isolda, 324 Bamberga, 354 Eleonora, 451 Patientia, 476 Hedwig, 511 Davida, 532 Herculina, 596 Scheila, 704 Interamnia Occultation Event: Asteroid 10 Hygiea – Sun 26th Feb 16h37m UT The magnitude 11 asteroid 10 Hygiea is expected to occult the magnitude 12.5 star 2UCAC 21608371 on Sunday 26th Feb 16h37m UT (= Mon 3:37am). Magnitude drop of 0.24 will require video. DAMIT asteroid model of 10 Hygiea - Astronomy Institute of the Charles University: Josef Ďurech, Vojtěch Sidorin Hygiea is the fourth-largest asteroid (largest is Ceres ~ 945kms) in the Solar System by volume and mass, and it is located in the asteroid belt about 400 million kms away.
    [Show full text]
  • Occdhtlm3newstelter
    OccdhtlM3Newstelter Volume II, Number 10 january, 1981 Occultation Newsletter is published by the International Occultation Timing Association. Editor and Compositor: H. F. DaBo11; 6 N 106 White Oak Lane; St. Charles, IL 60174; U.S.A. Please send editorial matters to the above, but send address changes, requests, matters of circulation, and other IOTA business to IOTA; P.0. Box 596; Tinley Park; IL 60477; U.S.A. NOTICE TO LUNAR OCCULTATION OBSERVERS paho1. by contacting Sr. Francisco Diego Q., Ixpan- tenco 26-bis, Real dc Ids Reyes, Coyoacdn, Mexico, L. V. Morrison D.F., Mexico. Currently, however, the Latin American Section is experiencing problems with funding, and On 1981 January 1 the international centre for the for the time being, it may be necessary for would-be receipt of timings of occultations of stars by the IOTA/LAS members to subscribe to the English-lan- Moon will be transferred from HM Nautical Almanac guage edition of o.n., or to join the parent IOTA. Office, Royal Greenwich Observatory, England to As- tronomical Division, Hydrographic Department, Japan IOTA NEWS "' From that date observers should send their lunar oc- cultation reports and any correspondence connected David W. Dunham with lunar occultations to the following address: As of 1981 January 1, H. M. Nautical Almanac Office, Astronomical Division at the Royal Greenwich Observatory, England, will Hydrographic Department discontinue collecting observations of lunar occul- Tsukiji-5 tations. After that date, observers should send Chuo-ku, Tokyo their reports to the new International Occultation 104 JAPAN Centre in japan, as described in this issue's lead article.
    [Show full text]
  • CAPTURE of TRANS-NEPTUNIAN PLANETESIMALS in the MAIN ASTEROID BELT David Vokrouhlický1, William F
    The Astronomical Journal, 152:39 (20pp), 2016 August doi:10.3847/0004-6256/152/2/39 © 2016. The American Astronomical Society. All rights reserved. CAPTURE OF TRANS-NEPTUNIAN PLANETESIMALS IN THE MAIN ASTEROID BELT David Vokrouhlický1, William F. Bottke2, and David Nesvorný2 1 Institute of Astronomy, Charles University, V Holešovičkách 2, CZ–18000 Prague 8, Czech Republic; [email protected] 2 Department of Space Studies, Southwest Research Institute, 1050 Walnut Street, Suite 300, Boulder, CO 80302; [email protected], [email protected] Received 2016 February 9; accepted 2016 April 21; published 2016 July 26 ABSTRACT The orbital evolution of the giant planets after nebular gas was eliminated from the Solar System but before the planets reached their final configuration was driven by interactions with a vast sea of leftover planetesimals. Several variants of planetary migration with this kind of system architecture have been proposed. Here, we focus on a highly successful case, which assumes that there were once five planets in the outer Solar System in a stable configuration: Jupiter, Saturn, Uranus, Neptune, and a Neptune-like body. Beyond these planets existed a primordial disk containing thousands of Pluto-sized bodies, ∼50 million D > 100 km bodies, and a multitude of smaller bodies. This system eventually went through a dynamical instability that scattered the planetesimals and allowed the planets to encounter one another. The extra Neptune-like body was ejected via a Jupiter encounter, but not before it helped to populate stable niches with disk planetesimals across the Solar System. Here, we investigate how interactions between the fifth giant planet, Jupiter, and disk planetesimals helped to capture disk planetesimals into both the asteroid belt and first-order mean-motion resonances with Jupiter.
    [Show full text]
  • The Minor Planet Bulletin
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 36, NUMBER 3, A.D. 2009 JULY-SEPTEMBER 77. PHOTOMETRIC MEASUREMENTS OF 343 OSTARA Our data can be obtained from http://www.uwec.edu/physics/ AND OTHER ASTEROIDS AT HOBBS OBSERVATORY asteroid/. Lyle Ford, George Stecher, Kayla Lorenzen, and Cole Cook Acknowledgements Department of Physics and Astronomy University of Wisconsin-Eau Claire We thank the Theodore Dunham Fund for Astrophysics, the Eau Claire, WI 54702-4004 National Science Foundation (award number 0519006), the [email protected] University of Wisconsin-Eau Claire Office of Research and Sponsored Programs, and the University of Wisconsin-Eau Claire (Received: 2009 Feb 11) Blugold Fellow and McNair programs for financial support. References We observed 343 Ostara on 2008 October 4 and obtained R and V standard magnitudes. The period was Binzel, R.P. (1987). “A Photoelectric Survey of 130 Asteroids”, found to be significantly greater than the previously Icarus 72, 135-208. reported value of 6.42 hours. Measurements of 2660 Wasserman and (17010) 1999 CQ72 made on 2008 Stecher, G.J., Ford, L.A., and Elbert, J.D. (1999). “Equipping a March 25 are also reported. 0.6 Meter Alt-Azimuth Telescope for Photometry”, IAPPP Comm, 76, 68-74. We made R band and V band photometric measurements of 343 Warner, B.D. (2006). A Practical Guide to Lightcurve Photometry Ostara on 2008 October 4 using the 0.6 m “Air Force” Telescope and Analysis. Springer, New York, NY. located at Hobbs Observatory (MPC code 750) near Fall Creek, Wisconsin.
    [Show full text]
  • Dynamical Evolution of the Cybele Asteroids
    MNRAS 451, 244–256 (2015) doi:10.1093/mnras/stv997 Dynamical evolution of the Cybele asteroids Downloaded from https://academic.oup.com/mnras/article-abstract/451/1/244/1381346 by Universidade Estadual Paulista J�lio de Mesquita Filho user on 22 April 2019 V. Carruba,1‹ D. Nesvorny,´ 2 S. Aljbaae1 andM.E.Huaman1 1UNESP, Univ. Estadual Paulista, Grupo de dinamicaˆ Orbital e Planetologia, 12516-410 Guaratingueta,´ SP, Brazil 2Department of Space Studies, Southwest Research Institute, Boulder, CO 80302, USA Accepted 2015 May 1. Received 2015 May 1; in original form 2015 April 1 ABSTRACT The Cybele region, located between the 2J:-1A and 5J:-3A mean-motion resonances, is ad- jacent and exterior to the asteroid main belt. An increasing density of three-body resonances makes the region between the Cybele and Hilda populations dynamically unstable, so that the Cybele zone could be considered the last outpost of an extended main belt. The presence of binary asteroids with large primaries and small secondaries suggested that asteroid families should be found in this region, but only relatively recently the first dynamical groups were identified in this area. Among these, the Sylvia group has been proposed to be one of the oldest families in the extended main belt. In this work we identify families in the Cybele region in the context of the local dynamics and non-gravitational forces such as the Yarkovsky and stochastic Yarkovsky–O’Keefe–Radzievskii–Paddack (YORP) effects. We confirm the detec- tion of the new Helga group at 3.65 au, which could extend the outer boundary of the Cybele region up to the 5J:-3A mean-motion resonance.
    [Show full text]
  • Composition of the L5 Mars Trojans: Neighbors, Not Siblings
    Composition of the L5 Mars Trojans: Neighbors, not Siblings Andrew S. Rivkin a,1, David E. Trilling b, Cristina A. Thomas c,1, Francesca DeMeo c, Timothy B. Spahr d, and Richard P. Binzel c,1 aJohns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Rd. Laurel, MD 20723 bSteward Observatory, The University of Arizona, Tucson, AZ 85721 cDepartment of Earth, Atmospheric, and Planetary Sciences, M.I.T. Cambridge, MA 02139 dHarvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge MA 02138 arXiv:0709.1925v1 [astro-ph] 12 Sep 2007 Number of pages: 14 Number of tables: 1 Number of figures: 6 Email address: [email protected] (Andrew S. Rivkin). 1 Visiting Astronomer at the Infrared Telescope Facility, which is operated by the University of Hawaii under Cooperative Agreement no. NCC 5-538 with the National Aeronautics and Space Administration, Science Mission Directorate, Planetary As- tronomy Program. Preprint submitted to Icarus 29 May 2018 Proposed Running Head: Characterization of Mars Trojans Please send Editorial Correspondence to: Andrew S. Rivkin Applied Physics Laboratory MP3-E169 Laurel, MD 20723-6099, USA. Email: [email protected] Phone: (778) 443-8211 2 ABSTRACT Mars is the only terrestrial planet known to have Trojan (co-orbiting) aster- oids, with a confirmed population of at least 4 objects. The origin of these objects is not known; while several have orbits that are stable on solar-system timescales, work by Rivkin et al. (2003) showed they have compositions that suggest separate origins from one another. We have obtained infrared (0.8-2.5 micron) spectroscopy of the two largest L5 Mars Trojans, and confirm and extend the results of Rivkin et al.
    [Show full text]
  • Elements of Astronomy
    ^ ELEMENTS ASTRONOMY: DESIGNED AS A TEXT-BOOK uabemws, Btminwcus, anb families. BY Rev. JOHN DAVIS, A.M. FORMERLY PROFESSOR OF MATHEMATICS AND ASTRONOMY IN ALLEGHENY CITY COLLEGE, AND LATE PRINCIPAL OF THE ACADEMY OF SCIENCE, ALLEGHENY CITY, PA. PHILADELPHIA: PRINTED BY SHERMAN & CO.^ S. W. COB. OF SEVENTH AND CHERRY STREETS. 1868. Entered, according to Act of Congress, in the year 1867, by JOHN DAVIS, in the Clerk's OlBce of the District Court of the United States for the Western District of Pennsylvania. STEREOTYPED BY MACKELLAR, SMITHS & JORDAN, PHILADELPHIA. CAXTON PRESS OF SHERMAN & CO., PHILADELPHIA- PREFACE. This work is designed to fill a vacuum in academies, seminaries, and families. With the advancement of science there should be a corresponding advancement in the facilities for acquiring a knowledge of it. To economize time and expense in this department is of as much importance to the student as frugality and in- dustry are to the success of the manufacturer or the mechanic. Impressed with the importance of these facts, and having a desire to aid in the general diffusion of useful knowledge by giving them some practical form, this work has been prepared. Its language is level to the comprehension of the youthful mind, and by an easy and familiar method it illustrates and explains all of the principal topics that are contained in the science of astronomy. It treats first of the sun and those heavenly bodies with which we are by observation most familiar, and advances consecutively in the investigation of other worlds and systems which the telescope has revealed to our view.
    [Show full text]
  • The Search for Water Ice on Comets and Asteroids
    UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FÍSICAS TESIS DOCTORAL The Search for water ice on Comets and Asteroids La búsqueda de hielo de agua en Cometas y Asteroides MEMORIA PARA OPTAR AL GRADO DE DOCTOR PRESENTADA POR Laurence O’Rourke DIRECTOR Michael Küppers Madrid © Laurence O’Rourke, 2021 UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FÍSICAS TESIS DOCTORAL La búsqueda de hielo de agua en Cometas y Asteroides MEMORIA PARA OPTAR AL GRADO DE DOCTOR PRESENTADA POR Laurence O’Rourke DIRECTOR Dr. Michael Küppers The Search for water ice on Comets and Asteroids La búsqueda de hielo de agua en Cometas y Asteroides TESIS DOCTORAL LAURENCE O’ROURKE Departamento de Física de la Tierra y Astrofísica Facultad de Ciencias Físicas Universidad Complutense de Madrid A thesis submitted for the degree of Doctor en Astrofisica September 2020 Director: Dr. Michael Küppers Tutor: Prof. David Montes Gutiérrez Dedication I would like to dedicate this thesis to my wife Cristina & our children David and Paulina, and to my parents, Laurence and Rita (neé Curley) O’Rourke, who have both passed away but who would no doubt have been very proud of me for this achievement. Acknowledgements This work has been possible thanks to the great support and help provided by my PhD director Michael Küppers and by my UCM tutor, David Montes Gutiérrez. The published papers presented, provide an excellent overview of the significant collaborations I have had across the planetary science community with nearly 50 different co-authors represented in the papers. Their professionalism, expertise and friendship were vital to ensure that the papers I wrote were at the highest level.
    [Show full text]
  • Accurate Positions of Pluto and Asteroids Observed in Bucharest During the Year 1932
    ACCURATE POSITIONS OF PLUTO AND ASTEROIDS OBSERVED IN BUCHAREST DURING THE YEAR 1932 GHEORGHE BOCŞA, PETRE POPESCU, MIHAELA LICULESCU Astronomical Institute of the Romanian Academy Str. Cuţitul de Argint 5, 040557 Bucharest, Romania E-mail: [email protected] Abstract. The paper contains the observations of minor planets performed in Bucharest Astronomical Observatory in the year 1932 with the 380/6000 mm astrograph. Both Turner’s (constants) and Schlesinger’s (dependences) methods were used in the computation of the normal coordinates of the objects. Keywords: photographic astrometry – minor planets. 1. INTRODUCTION The article is a continuation of the complete investigation of Bucharest Wide-Field Plates Archive initiated in 2010; it contains the plates with asteroids observed in 1932. That year 185 plates were exposed and were stored in the archive, but were not reduced. After analysing them, 98 plates were detected to contain measurable minor planets. The first observed positions in this year were of planet Pluto. They were exposed on 1318cm plates, with 52 minutes exposure .The observations were performed by the famous Romanian astronomer Professor Gheorghe Demetrescu. The most difficult problem was the identification of the planet, the three plates obtained in 1932 having dozens of stars with up to 15 magnitudes. As all the observations were performed in the same month and the planet did not have a great proper motion, it was possible to superpose two plates and to identify Pluto. The values (O–C)α and (O–C)δ were calculated by M. Svechnikov from the Institute of Applied Astronomy in Sankt Petersburg on the basis of precise positions obtained in Bucharest, which we integrated in Pluto’s orbit.
    [Show full text]
  • Planetary Science Institute
    PLANETARY SCIENCE INSTITUTE N7'6-3qo84 (NAS A'-CR:1'V7! 3 ) ASTEROIDAL AND PLANETARY ANALYSIS Final Report (Planetary Science Ariz.) 163 p HC $6.75 Inst., Tucson, CSCL 03A Unclas G3/89 15176 i-'' NSA tiFACIWj INP BRANC NASW 2718 ASTEROIDAL AND PLANETARY ANALYSIS Final Report 11 August 1975 Submitted by: Planetary Science Institute 252 W. Ina Road, Suite D Tucson, Arizona 85704 William K. Hartmann Manager TASK 1: ASTEROID SPECTROPHOTOMETRY AND INTERPRETATION (Principal Investigator: Clark R. Chapman) A.* INTRODUCTION The asteroid research program during 1974/5 has three major goals: (1) continued spectrophotometric reconnaissance of the asteroid belt to define compositional types; (2) detailed spectrophotometric observations of particular asteroids, especially to determine variations with rotational phase, if any; and (3) synthesis of these data with other physical studies of asteroids and interpretation of the implications of physical studies of the asteroids for meteoritics and solar system history. The program has been an especially fruitful one, yielding fundamental new insights to the nature of the asteroids and the implications for the early development of the terrestrial planets. In particular, it is believed that the level of understanding of the asteroids has been reached, and sufficiently fundamental questions raised about their nature, that serious consideration should be given to possible future spacecraft missions directed to study a sample of asteroids at close range. Anders (1971) has argued that serious consideration of asteroid missions should be postponed until ground-based techniques for studying asteroids had been sufficiently exploited so that we could intelligently select appropriate asteroids for spacecraft targeting. It is clear that that point has been reached, ,and now that relatively inexpensive fly-by missions have been discovered to be possible by utilizing Venus and Earth gravity assists (Bender and Friedlander, 1975), serious planning for such missions ought to begin.
    [Show full text]
  • Iso and Asteroids
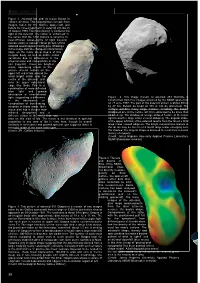
    r bulletin 108 Figure 1. Asteroid Ida and its moon Dactyl in enhanced colour. This colour picture is made from images taken by the Galileo spacecraft just before its closest approach to asteroid 243 Ida on 28 August 1993. The moon Dactyl is visible to the right of the asteroid. The colour is ‘enhanced’ in the sense that the CCD camera is sensitive to near-infrared wavelengths of light beyond human vision; a ‘natural’ colour picture of this asteroid would appear mostly grey. Shadings in the image indicate changes in illumination angle on the many steep slopes of this irregular body, as well as subtle colour variations due to differences in the physical state and composition of the soil (regolith). There are brighter areas, appearing bluish in the picture, around craters on the upper left end of Ida, around the small bright crater near the centre of the asteroid, and near the upper right-hand edge (the limb). This is a combination of more reflected blue light and greater absorption of near-infrared light, suggesting a difference Figure 2. This image mosaic of asteroid 253 Mathilde is in the abundance or constructed from four images acquired by the NEAR spacecraft composition of iron-bearing on 27 June 1997. The part of the asteroid shown is about 59 km minerals in these areas. Ida’s by 47 km. Details as small as 380 m can be discerned. The moon also has a deeper near- surface exhibits many large craters, including the deeply infrared absorption and a shadowed one at the centre, which is estimated to be more than different colour in the violet than any 10 km deep.
    [Show full text]
  • IRTF Spectra for 17 Asteroids from the C and X Complexes: a Discussion of Continuum Slopes and Their Relationships to C Chondrites and Phyllosilicates ⇑ Daniel R
    Icarus 212 (2011) 682–696 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus IRTF spectra for 17 asteroids from the C and X complexes: A discussion of continuum slopes and their relationships to C chondrites and phyllosilicates ⇑ Daniel R. Ostrowski a, Claud H.S. Lacy a,b, Katherine M. Gietzen a, Derek W.G. Sears a,c, a Arkansas Center for Space and Planetary Sciences, University of Arkansas, Fayetteville, AR 72701, United States b Department of Physics, University of Arkansas, Fayetteville, AR 72701, United States c Department of Chemistry and Biochemistry, University of Arkansas, Fayetteville, AR 72701, United States article info abstract Article history: In order to gain further insight into their surface compositions and relationships with meteorites, we Received 23 April 2009 have obtained spectra for 17 C and X complex asteroids using NASA’s Infrared Telescope Facility and SpeX Revised 20 January 2011 infrared spectrometer. We augment these spectra with data in the visible region taken from the on-line Accepted 25 January 2011 databases. Only one of the 17 asteroids showed the three features usually associated with water, the UV Available online 1 February 2011 slope, a 0.7 lm feature and a 3 lm feature, while five show no evidence for water and 11 had one or two of these features. According to DeMeo et al. (2009), whose asteroid classification scheme we use here, 88% Keywords: of the variance in asteroid spectra is explained by continuum slope so that asteroids can also be charac- Asteroids, composition terized by the slopes of their continua.
    [Show full text]