DOCSLIB.ORG

Calculus II Chapter 9 Review Name______

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Calculus II Chapter 9 Review Name______ Calculus II Chapter 9 Review Name___________ ________________________ SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence. an 1) a = 1, a = 1) 1 n+1 n + 2 Find a formula for the nth term of the sequence. 1 1 1 1 2) 1, - , , - , 2) 4 9 16 25 Find the limit of the sequence if it converges; otherwise indicate divergence. 9 + 8n 3) a = 3) n 9 + 5n 3 4) (-1)n 1 - 4) n Determine if the sequence is bounded. Δn 5) 5) 4n Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges. 3 3 3 3 6) 3 - + - + ... + (-1)n-1 + ... 6) 8 64 512 8n-1 7 7 7 7 7) + + + ... + + ... 7) 1·3 2·4 3·5 n(n + 2) Find the sum of the series. Q n 9 8) _ (-1) 8) 4n n=0 Use partial fractions to find the sum of the series. 3 9) 9) _ (4n - 1)(4n + 3) 1 Determine if the series converges or diverges; if the series converges, find its sum. 3n+1 10) _ 10) 7n-1 1 cos nΔ 11) _ 11) 7n Find the values of x for which the geometric series converges. n n 12) _ -3 x 12) Find the sum of the geometric series for those x for which the series converges. 13) (6x)2n 13) n 14) _ (x + 2) 14) Use the integral test to determine whether the series converges. 15) 15) _ n 7 16) _ 16) ex - 1 Use the direct comparison test to determine if the series converges or diverges. Q 10 17) 17) _ 3 n=1 7 n + 8 n 5 + 2 cos n 18) 18) _ 4 Q n (-1)n n=0 Use the limit comparison test to determine if the series converges or diverges. 5 + 8 sin n 19) _ 19) 9n5/4 + 5 cos n 1 1 20) 20) _ 4 + 7n ln n 3 Use the ratio test to determine if the series converges or diverges. 21) n! e-6n 21) 2 9(n!)2 22) 22) _ (2n)! Use the root test to determine if the series converges or diverges. ln n n 23) 23) _ 3n 10 n 24) _ 24) 5n1/n - 1 n Determine convergence or divergence of the series. a 6 25) _ 25) (5n + 8)4/3 3n1/2 26) _ 26) 4 3/2 + 2 Determine if the series defined by the formula converges or diverges. 8 + sin n 27) = 2, a = a 27) 1 n+1 n n n 28) a 28) n + 1 n Determine convergence or divergence of the alternating series. (-1)n 29) _ 29) 6 4 + 2 Q (-1)n 5n6 + 6 30) _ 30) n= 3n2 + 6 Determine eithern absolute convergence, conditional convergence or divergence for the series. 2 5 31) - 31) 1 6 6 8 5n + 7 32) ln 32) _ 5n + 6 3 (n!) 7n 33) 33) _ (5n + 1)! Estimate the magnitude of the error involved in using the sum of the first four terms to approximate the sum of the entire series. n +1 1 34) _ 34) 4n Find the infinite sum accurate to 3 decimal places. +Q ( 1 35) (-1)n+1 35) _ (2n)! = 1 n Find the interval_ (x of convergence) of the series. (x - 4)n 36) 36) _ 6 + 8 7 2n 37) _ 37) 4n For what values of x does the series converge absolutely? n 38) _ 8x + 3) 38) For what values of x does the series converge conditionally? 2 xn 39) 39) _ n! Q 40) (-1)n 40) _ n n=0 Find the sum of the series as a function of x. 41) - 6 2 41) 1 x 3 n 42) 42) _ n6 Find the Taylor polynomial of order 3 generated by f at a. 1 43) f(x) = , a = 0 43) x + 2 4 44) f(x) = ln(x + 1), a = 7 44) Find the Maclaurin series for the given function. 45) e6x 45) 1 46) 46) x - 2 47) sin 7x 47) Find the Taylor series generated by f at x = a. 1 48) , a = 4 48) 49) f(x) = e4x, a = 8 49) Find the quadratic approximation of f at x = 0. 50) f(x) = 64 - x2 50) Use substitution to find the Taylor series at x = 0 of the given function. 51) -4x 51) Find the Taylor series for the given function. 52) x7 ex 52) 53) cos2 2x 53) 1 54) f(x) = 54) (1 - 7x)2 Solve the problem. 55) The polynomial 1 + 7x + 21x2 is used to approximate f(x) = (1 + x)7 on the interval 55) -0.01 K x K 0.01. Use the Remainder Estimation Theorem to estimate the maximum absolute error. Find the Taylor polynomial of lowest degree that will approximate F(x) throughout the given interval with an error of magnitude less than than 10-3. x sin t 56) F(x) = dt , [0, 1] 56) a t 0 Use series to evaluate the limit. e-5x - 1 57) lim 57) x0 x f(x) = x 5 58) lim x2 e2/x2 - 1 58) xQ Find the first four terms of the binomial series for the given function. 59) (1 + 6x)1/2 59) x -2/3 60) 1 - 60) 3 1 d 1 61) Use the binomial series and the fact that tanh-1 x = to generate the first 61) dx a 1- x2 -1 four nonzero terms of the Taylor series for tanh-1 x. Use the first three terms of the series to estimate tanh-1 (0.5). Solve the problem. 6 Answer Key Testname: CYCALCH.9R 1 1 1 1 1) 1, , , , 3 12 60 360 (-1)n+1 2) an = n2 8 3) 5 4) Diverges 5) bounded 1 31 - n (-8) 8 6) ; 1 3 1 + 8 7n(3n + 5) 21 7) ; 4(n + 1)(n + 2) 4 36 8) 5 1 9) 4 63 10) Converges; 4 7 11) Converges; 8 1 12) |x| < 3 1 13) 1 + 36x2 1 14) -1 - x 15) diverges 16) converges 17) Diverges 18) Converges 19) Converges 20) Diverges 21) Diverges 22) Converges 23) Converges 24) Converges 25) Converges 26) Diverges 27) Converges 28) Diverges 29) Converges 30) Diverges 31) Converges absolutely 32) Converges conditionally 7 Answer Key Testname: CYCALCH.9R 33) diverges 34) 9.77 × 10-4 35) 0.460 36) 3 ≤ x < 5 37) 5 < x < 9 1 1 38) - < x < - 2 4 39) None 40) x = 3 1 41) - x - 7 6 42) - x - 9 1 x x2 x3 43) - + - 2 4 8 16 x - 7 (x - 7)2 (x - 7)3 44) ln 8 + - + 8 128 1536 ∞ 6n xn 45) ∑ n! n=0 ∞ xn 46) - ∑ 2n+1 n=0 ∞ (-1)n 72n+1 x2n+1 47) ∑ (2n + 1)! n=0 ∞ (-1)n (x - 4)n 48) ∑ 4n+1 n=0 ∞ e32 4n (x - 8)n 49) ∑ n! n=0 x2 50) Q(x) = 8 - 16 ∞ (-1)n(4)nxn 51) ∑ n! n=0 ∞ xn+7 52) ∑ n! n=0 ∞ 1 (-1)n (4)2n x2n 53) + 2 ∑ 2(2n)! n=0 ∞ 54) ∑ (n+1) 7n xn n=0 55) ≈ 3.642 x 10-5 8 Answer Key Testname: CYCALCH.9R x3 x5 56) x - + 18 600 57) -5 58) 2 9 27 59) 1 + 3x - x2 + x3 2 2 2 5 40 60) 1 + x + x2 + x3 9 81 2187 x3 x5 x7 61) x + - + ; 0.535 3 5 7 9.
Load more

Recommended publications
  • Series: Convergence and Divergence Comparison Tests
    Series: Convergence and Divergence Here is a compilation of what we have done so far (up to the end of October) in terms of convergence and divergence. • Series that we know about: P∞ n Geometric Series: A geometric series is a series of the form n=0 ar . The series converges if |r| < 1 and 1 a1 diverges otherwise . If |r| < 1, the sum of the entire series is 1−r where a is the first term of the series and r is the common ratio. P∞ 1 2 p-Series Test: The series n=1 np converges if p1 and diverges otherwise . P∞ • Nth Term Test for Divergence: If limn→∞ an 6= 0, then the series n=1 an diverges. Note: If limn→∞ an = 0 we know nothing. It is possible that the series converges but it is possible that the series diverges. Comparison Tests: P∞ • Direct Comparison Test: If a series n=1 an has all positive terms, and all of its terms are eventually bigger than those in a series that is known to be divergent, then it is also divergent. The reverse is also true–if all the terms are eventually smaller than those of some convergent series, then the series is convergent. P P P That is, if an, bn and cn are all series with positive terms and an ≤ bn ≤ cn for all n sufficiently large, then P P if cn converges, then bn does as well P P if an diverges, then bn does as well. (This is a good test to use with rational functions.
    [Show full text]
  • MATH 162: Calculus II Differentiation
    MATH 162: Calculus II Framework for Mon., Jan. 29 Review of Differentiation and Integration Differentiation Definition of derivative f 0(x): f(x + h) − f(x) f(y) − f(x) lim or lim . h→0 h y→x y − x Differentiation rules: 1. Sum/Difference rule: If f, g are differentiable at x0, then 0 0 0 (f ± g) (x0) = f (x0) ± g (x0). 2. Product rule: If f, g are differentiable at x0, then 0 0 0 (fg) (x0) = f (x0)g(x0) + f(x0)g (x0). 3. Quotient rule: If f, g are differentiable at x0, and g(x0) 6= 0, then 0 0 0 f f (x0)g(x0) − f(x0)g (x0) (x0) = 2 . g [g(x0)] 4. Chain rule: If g is differentiable at x0, and f is differentiable at g(x0), then 0 0 0 (f ◦ g) (x0) = f (g(x0))g (x0). This rule may also be expressed as dy dy du = . dx x=x0 du u=u(x0) dx x=x0 Implicit differentiation is a consequence of the chain rule. For instance, if y is really dependent upon x (i.e., y = y(x)), and if u = y3, then d du du dy d (y3) = = = (y3)y0(x) = 3y2y0. dx dx dy dx dy Practice: Find d x d √ d , (x2 y), and [y cos(xy)]. dx y dx dx MATH 162—Framework for Mon., Jan. 29 Review of Differentiation and Integration Integration The definite integral • the area problem • Riemann sums • definition Fundamental Theorem of Calculus: R x I: Suppose f is continuous on [a, b].
    [Show full text]
  • Calculus 141 Section 9.6 Lecture Notes
    Calculus 141, section 9.6 Ratio Test and Root Tests notes by Tim Pilachowski ∞ c r m ● The geometric series ∑ c r n = if and only if r <1. n = m 1 − r ∞ 1 ● The p-series converges whenever p > 1 and diverges whenever 0 < p ≤ 1. ∑ p n =1 n ∞ ∞ ● The Integral Test states a series a converges if and only if f ()x dx converges. ∑ n ∫1 n =1 ∞ ● In the Direct Comparison Test, ∑ an converges if its terms are less than those of a known convergent n =1 series, and diverges if its terms are greater than those of a known convergent series. ∞ an ● The Limit Comparison Test states: If lim exists and is a positive number, then positive series ∑ an n → ∞ bn n =1 ∞ and ∑ bn either both converge or both diverge. n =1 A downside to the Comparison Tests is that they require a suitable series to use for the comparison. In contrast, the Ratio Test and the Root Test require only the series itself. ∞ ∞ an+1 Ratio Test (Theorem 9.15) Given a positive series an for which lim = r : a. If 0 ≤ r < 1, then an ∑ n→∞ ∑ n =1 an n =1 ∞ an+1 converges. b. If r > 1, then an diverges. c. If r = 1 or lim does not exist, no conclusion. ∑ n→∞ n =1 an The proof of part a. relies upon the definition of limits and the “creation” of a geometric series which converges to which we compare our original series. Briefly, by the nature of inequalities there exists a value s for which an+1 0 ≤ r < s < 1.
    [Show full text]
  • MATH 166 TEST 3 REVIEW SHEET General Comments and Advice
    MATH 166 TEST 3 REVIEW SHEET General Comments and Advice: The student should regard this review sheet only as a sample of potential test problems, and not an end-all-be-all guide to its content. Anything and everything which we have discussed in class is fair game for the test. The test will cover roughly Sections 10.1, 10.2, 10.3, 10.4, and 10.5. Don't limit your studying to this sheet; if you feel you don't fully understand a particular topic, then try to do more problems out of your textbook! Summary of Relative Growth Rates. For two sequences (an) and (bn) such that (an) ! 1 and (bn) ! 1, let the symbols (an) << (bn) denote that (bn) grows faster than (an). Then the following is a summary of our most commonly encountered growth rates: (ln n) << ((ln n)r) << (nq) << (n) << (np) << (bn) << (n!) << (nn), where r > 1, 0 < q < 1, p > 1, and b > 1. General Strategy for Determining Convergence of a Series. There is no hard and fast rule for determining whether a series converges or diverges, and in general the student should build up their own intuition on the subject through practice. However, the following mental checklist can be a helpful guideline. 1 X (1) Divergence Test. Given a series an, the first thing one should always n=1 ask is, do the terms (an) ! 0? If not, we are done and the series diverges by the DT. If the terms do shrink to zero, however, we have to put more thought into the problem.
    [Show full text]
  • The Direct Comparison Test (Day #1)
    9.4--The Direct Comparison Test (day #1) When applying the Direct Comparison Test, you will usually compare a tricky series against a geometric series or a p-series whose convergence/divergence is already known. Use the Direct Comparison Test to determine the convergence or divergence of the series: ∞ 1) 1 3 n + 7 n=1 9.4--The Direct Comparison Test (day #1) Use the Direct Comparison Test to determine the convergence or divergence of the series: ∞ 2) 1 n - 2 n=3 Use the Direct Comparison Test to determine the convergence or divergence of the series: ∞ 3) 5n n 2 - 1 n=1 9.4--The Direct Comparison Test (day #1) Use the Direct Comparison Test to determine the convergence or divergence of the series: ∞ 4) 1 n 4 + 3 n=1 9.4--The Limit Comparison Test (day #2) The Limit Comparison Test is useful when the Direct Comparison Test fails, or when the series can't be easily compared with a geometric series or a p-series. 9.4--The Limit Comparison Test (day #2) Use the Limit Comparison Test to determine the convergence or divergence of the series: 5) ∞ 3n2 - 2 n3 + 5 n=1 Use the Limit Comparison Test to determine the convergence or divergence of the series: 6) ∞ 4n5 + 9 10n7 n=1 9.4--The Limit Comparison Test (day #2) Use the Limit Comparison Test to determine the convergence or divergence of the series: 7) ∞ 1 n 4 - 1 n=1 Use the Limit Comparison Test to determine the convergence or divergence of the series: 8) ∞ 5 3 2 n - 6 n=1 9.4--Comparisons of Series (day #3) (This is actually a review of 9.1-9.4) page 630--Converging or diverging? Tell which test you used.
    [Show full text]
  • Direct and Limit Comparison Tests
    Joe Foster Direct and Limit Comparison Tests We have seen that a given improper integral converges if its integrand is less than the integrand of another integral known to converge. Similarly, a given improper integral diverges if its integrand is greater than the integrand of another integral known to diverge. We now apply the same idea to infinite series instead. Direct Comparison Test for Series: If0 a b for all n N, for some N, then, ≤ n ≤ n ≥ ∞ ∞ 1. If bn converges, then so does an. nX=1 nX=1 ∞ ∞ 2. If an diverges, then so does bn. nX=1 nX=1 a The Limit Comparison Test: Suppose a > 0 and b > 0 for all n. If lim n = L, where L is finite and L> 0, then n n →∞ n bn the two series an and bn either both converge or both diverge. X X ∞ 1 Example 1: Determine whether the series converges or diverges. 2n + n nX=1 1 1 We have for all n 1. So, 2n + n ≤ 2n ≥ ∞ ∞ 1 1 . 2n + n ≤ 2n nX=1 nX=1 1 Since the series on the right is a geometric series with r = , it converges. So we determine that our series of interest also 2 converges. ∞ 1 Example 2: Determine whether the series converges or diverges. n2 + n +1 nX=1 1 1 We have for all n 1. So, n2 + n +1 ≤ n2 ≥ ∞ ∞ 1 1 . n2 + n +1 ≤ n2 nX=1 nX=1 Since the series on the right is a p series with p = 2 > 1, it converges.
    [Show full text]
  • Comparison Tests for Integrals
    Joe Foster Direct and Limit Comparison Tests Tests for Convergence: When we cannot evaluate an improper integral directly, we try to determine whether it con- verges of diverges. If the integral diverges, we are done. If it converges we can use numerical methods to approximate its value. The principal tests for convergence or divergence are the Direct Comparison Test and the Limit Comparison Test. Direct Comparison Test for Integrals: If0 ≤ f(x) ≤ g(x) on the interval (a, ∞], where a ∈ R, then, ∞ ∞ 1. If g(x) dx converges, then so does f(x) dx. ˆa ˆa ∞ ∞ 2. If f(x) dx diverges, then so does g(x) dx. ˆa ˆa Why does this make sense? 1. If the area under the curve of g(x) is finite and f(x) is bounded above by g(x) (and below by 0), then the area under the curve of f(x) must be less than or equal to the area under the curve of g(x). A positive number less that a finite number is also finite. 2. If the area under the curve of f(x) is infinite and g(x) is bounded below by f(x), then the area under the curve of g(x) must be “less than or equal to” the area under the curve of g(x). Since there is no finite number “greater than” infinity, the area under g(x) must also be infinite. Example 1: Determine if the following integral is convergent or divergent. ∞ cos2(x) 2 dx. ˆ2 x cos2(x) cos2(x) We want to find a function g(x) such that for some a ∈ R, f(x)= ≤ g(x) or f(x)= ≥ g(x) for all x ≥ a.
    [Show full text]
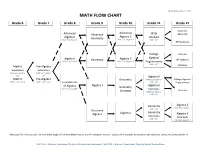
  • Math Flow Chart
    Updated November 12, 2014 MATH FLOW CHART Grade 6 Grade 7 Grade 8 Grade 9 Grade 10 Grade 11 Grade 12 Calculus Advanced Advanced Advanced Math AB or BC Algebra II Algebra I Geometry Analysis MAP GLA-Grade 8 MAP EOC-Algebra I MAP - ACT AP Statistics College Calculus Algebra/ Algebra I Geometry Algebra II AP Statistics MAP GLA-Grade 8 MAP EOC-Algebra I Trigonometry MAP - ACT Math 6 Pre-Algebra Statistics Extension Extension MAP GLA-Grade 6 MAP GLA-Grade 7 or or Algebra II Math 6 Pre-Algebra Geometry MAP EOC-Algebra I College Algebra/ MAP GLA-Grade 6 MAP GLA-Grade 7 MAP - ACT Foundations Trigonometry of Algebra Algebra I Algebra II Geometry MAP GLA-Grade 8 Concepts Statistics Concepts MAP EOC-Algebra I MAP - ACT Geometry Algebra II MAP EOC-Algebra I MAP - ACT Discovery Geometry Algebra Algebra I Algebra II Concepts Concepts MAP - ACT MAP EOC-Algebra I Additional Full Year Courses: General Math, Applied Technical Mathematics, and AP Computer Science. Calculus III is available for students who complete Calculus BC before grade 12. MAP GLA – Missouri Assessment Program Grade Level Assessment; MAP EOC – Missouri Assessment Program End-of-Course Exam Mathematics Objectives Calculus Mathematical Practices 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Linear and Nonlinear Functions • Write equations of linear and nonlinear functions in various formats.
    [Show full text]
  • Which Convergence Test Should I Use?
    Which Convergence Test Should I Use? 1 X 1. Is the series a geometric series? I.e. arn. n=0 Then: Converges for jrj < 1 and diverges otherwise. 1 X 1 2. Is the series a p-series? I.e. np n=0 Then: Converges for p > 1 and diverges otherwise. 3. Check the nth Term Divergence Test. Then: Diverges if lim an 6= 0. No information, otherwise. n!1 4. Is the series a positive series? I.e. an ≥ 0 for all n. Then: Check the following tests, in order. (a) The Direct Comparison Test: Can you find a larger series that converges or a smaller series which diverges? This is usually done by dropping terms from the numerator or denominator. 1 1 1 1 I.e. p < , but p > . n2 + n n2 n2 − n n2 Then: Larger series converging implies convergence, and smaller series diverging implies diver- gence. (b) The Limit Comparison Test: Can you find a comparison with a known convergent or divergent series, but the inequality is the wrong way for the Direct Comparison Test? Consider the \dom- 1 1 inant" term in the series. I.e. p is dominated by n2, so compare with . n2 − n n2 an X X Then: Consider lim = L. If L > 0, an and bn both converge or both diverge. If n!1 bn X X X L = 0, convergence of bn implies convergence of an. If L = 1, convergence of an X implies convergence of bn. (c) The Ratio Test: Does the series contain terms with factorials (i.e n!) or exponentials (i.e.
    [Show full text]
  • Of 13 MATH 1C: EXAM INFORMATION for SEQUENCES and SERIES (SS) LESSONS
    MATH 1C: EXAM INFORMATION FOR MULTIVARIABLE DIFFERENTIATION (MD) LESSONS MD LESSONS 0: THE LEAST-SQUARES PROBLEM ☐ Discuss the major themes of part 1 of Math 1C: State the limit definition of the ordinary derivative from Math 1A. State the second derivative test from Math 1A. Given a single variable function, find the maximum and minimum values of this function using the second derivative test from Math 1A. Describe the forward and backward problems of single-variable differentiation. Make explicit connections to the work you did in Math 1AB. Describe the forward and backward problems of multivariable-variable differentiation. Make explicit connections to the work you will do in Math 1CD. Compare and contrast single-variable differentiation with multivariable differentiation. Construct a linear least-squares problem using a given data set. Make sure you can • Set up a model for the error �! between the ith data point (�!, �!) and any associated linear model � = � � = �� + �. • Using the model for the errors, set up the least-squares problem for this input data. In particular, create a two variable function �!(�, �) that you can use to solve create the ``best-fit'' model for this data. Explain in detail the choices that you made to construct your error function �!. Why do you use the total squared error (and not the sum of the individual errors �! or the sum of the absolute value of the individual errors �! )? • Explain how we will use multivariable calculus to find the line of best fit. Make explicit connections with the second
    [Show full text]
  • Math 131Infinite Series, Part IV: the Limit Comparisontest
    21 The Limit Comparison Test While the direct comparison test is very useful, there is another comparison test that focuses only on the tails of the series that we want to compare. This makes it more widely applicable and simpler to use. We don’t need to verify that an ≤ bn for all (or most) n. However, it will require our skills in evaluating limits at infinity! THEOREM 14.7 (The Limit Comparison Test). Assume that an > 0 and bn > 0 for all n (or at least all n ≥ k) and that a lim n = L. n!¥ bn ¥ (1) If 0 < L < ¥ (i.e., L is a positive, finite number), then either the series ∑ an and n=1 ¥ ∑ bn both converge or both diverge. n=1 ¥ ¥ (2) If L = 0 and ∑ bn converges, then ∑ an converges. n=1 n=1 ¥ ¥ (3) If L = ¥ and ∑ bn diverges, then ∑ an diverges. n=1 n=1 an The idea of the theorem is since lim = L, then eventually an ≈ Lbn. So if one n!¥ bn of the series converges (diverges) so does the other since the two are ‘essentially’ scalar multiples of each other. ¥ 1 EXAMPLE 14.19. Does converge? ∑ 2 − + n=1 3n n 6 SOLUTION. scrap work: Let’s apply the limit comparison test. Notice that the terms are always positive since the polynomial 3n2 − n + 6 has no roots. In any event, the terms are eventually positive since this an upward-opening parabola. If we focus on ¥ 1 highest powers, then the series looks a like the p-series ∑ 2 which converges.
    [Show full text]
  • INTRODUCTION of INFINITE SERIES in HIGH SCHOOL LEVEL CALCULUS Ericka Bella John Carroll University, [email protected]
    John Carroll University Carroll Collected Masters Essays Master's Theses and Essays Summer 2019 INTRODUCTION OF INFINITE SERIES IN HIGH SCHOOL LEVEL CALCULUS Ericka Bella John Carroll University, [email protected] Follow this and additional works at: https://collected.jcu.edu/mastersessays Part of the Mathematics Commons Recommended Citation Bella, Ericka, "INTRODUCTION OF INFINITE SERIES IN HIGH SCHOOL LEVEL CALCULUS" (2019). Masters Essays. 122. https://collected.jcu.edu/mastersessays/122 This Essay is brought to you for free and open access by the Master's Theses and Essays at Carroll Collected. It has been accepted for inclusion in Masters Essays by an authorized administrator of Carroll Collected. For more information, please contact [email protected]. INTRODUCTION OF INFINITE SERIES IN HIGH SCHOOL LEVEL CALCULUS An Essay Submitted to the Office of Graduate Studies College of Arts & Sciences of John Carroll University In Partial Fulfillment of the Requirements For the Degree of Master of Arts By Ericka L. Bella 2019 The essay of Ericka L. Bella is hereby accepted: ___________________________________________ _____________________ Advisor – Barbara K. D’Ambrosia Date I certify that this is the original document ___________________________________________ _____________________ Author – Ericka L. Bella Date Table of Contents Introduction ..........................................................................................................................1 Lesson 1: Introduction to Sequences and Series Teacher Notes ...................................................................................................................3
    [Show full text]