Transformation Models: the Tram Package
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Free Tram Zone
Melbourne’s Free Tram Zone Look for the signage at tram stops to identify the boundaries of the zone. Stop 0 Stop 8 For more information visit ptv.vic.gov.au Peel Street VICTORIA ST Victoria Street & Victoria Street & Peel Street Carlton Gardens Stop 7 Melbourne Star Observation Wheel Queen Victoria The District Queen Victoria Market ST ELIZABETH Melbourne Museum Market & IMAX Cinema t S n o s WILLIAM ST WILLIAM l o DOCKLANDS DR h ic Stop 8 N Melbourne Flagstaff QUEEN ST Gardens Central Station Royal Exhibition Building St Vincent’s LA TROBE ST LA TROBE ST VIC. PDE Hospital SPENCER ST KING ST WILLIAM ST ELIZABETH ST ST SWANSTON RUSSELL ST EXHIBITION ST HARBOUR ESP HARBOUR Flagstaff Melbourne Stop 0 Station Central State Library Station VICTORIA HARBOUR WURUNDJERI WAY of Victoria Nicholson Street & Victoria Parade LONSDALE ST LONSDALE ST Stop 0 Parliament Station Parliament Station VICTORIA HARBOUR PROMENADE Nicholson Street Marvel Stadium Library at the Dock SPRING ST Parliament BOURKE ST BOURKE ST BOURKE ST House YARRA RIVER COLLINS ST Old Treasury Southern Building Cross Station KING ST WILLIAM ST ST MARKET QUEEN ST ELIZABETH ST ST SWANSTON RUSSELL ST EXHIBITION ST COLLINS ST SPENCER ST COLLINS ST COLLINS ST Stop 8 St Paul’s Cathedral Spring Street & Collins Street Fitzroy Gardens Immigration Treasury Museum Gardens WURUNDJERI WAY FLINDERS ST FLINDERS ST Stop 8 Spring Street SEA LIFE Melbourne & Flinders Street Aquarium YARRA RIVER Flinders Street Station Federation Square Stop 24 Stop Stop 3 Stop 6 Don’t touch on or off if Batman Park Flinders Street Federation Russell Street Eureka & Queensbridge Tower Square & Flinders Street you’re just travelling in the SkyDeck Street Arts Centre city’s Free Tram Zone. -

Interstate Commerce Commission Washington
INTERSTATE COMMERCE COMMISSION WASHINGTON REPORT NO. 3374 PACIFIC ELECTRIC RAILWAY COMPANY IN BE ACCIDENT AT LOS ANGELES, CALIF., ON OCTOBER 10, 1950 - 2 - Report No. 3374 SUMMARY Date: October 10, 1950 Railroad: Pacific Electric Lo cation: Los Angeles, Calif. Kind of accident: Rear-end collision Trains involved; Freight Passenger Train numbers: Extra 1611 North 2113 Engine numbers: Electric locomo tive 1611 Consists: 2 muitiple-uelt 10 cars, caboose passenger cars Estimated speeds: 10 m. p h, Standing ft Operation: Timetable and operating rules Tracks: Four; tangent; ] percent descending grade northward Weather: Dense fog Time: 6:11 a. m. Casualties: 50 injured Cause: Failure properly to control speed of the following train in accordance with flagman's instructions - 3 - INTERSTATE COMMERCE COMMISSION REPORT NO, 3374 IN THE MATTER OF MAKING ACCIDENT INVESTIGATION REPORTS UNDER THE ACCIDENT REPORTS ACT OF MAY 6, 1910. PACIFIC ELECTRIC RAILWAY COMPANY January 5, 1951 Accident at Los Angeles, Calif., on October 10, 1950, caused by failure properly to control the speed of the following train in accordance with flagman's instructions. 1 REPORT OF THE COMMISSION PATTERSON, Commissioner: On October 10, 1950, there was a rear-end collision between a freight train and a passenger train on the Pacific Electric Railway at Los Angeles, Calif., which resulted in the injury of 48 passengers and 2 employees. This accident was investigated in conjunction with a representative of the Railroad Commission of the State of California. 1 Under authority of section 17 (2) of the Interstate Com merce Act the above-entitled proceeding was referred by the Commission to Commissioner Patterson for consideration and disposition. -
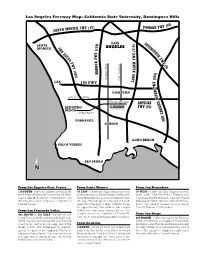
Freeway and Campus Combo
Los Angeles Freeway Map: California State University, Dominguez Hills 0) ) Y (1 ONICA FWY (10 POMONA FW SANTA M ) LOS I ) N 0 SANTA 0 T 1 E MONICA S ANGELES 1 R 1 A 7 ( S N ( T A Y D Y T I E E W G W F F O F W F R Y H W O C (5 Y B A ) R ( E 4 A B 0 ) H 5 G 5 ) 0 N 6 Avalon Blvd. ( Central Ave. O LAX L 105 FWY Y W W F F R R E COMPTON E V V I Artesia Blvd. I R R L Victoria Street L E ARTESIA E I I R REDONDO FWY (91) R B B A BEACH A G 190th Street G N N A A S TORRANCE S CARSON LONG BEACH PALOS VERDES SAN PEDRO N ➢ From Los Angeles Civic Center From Santa Monica From San Bernadino 110 SOUTH - Follow the Harbor Freeway (110) 10 EAST - Follow the Santa Monica Freeway 10 WEST - Follow the San Gabriel Freeway to the Artesia Freeway (91) east to Avalon Blvd. (10) east to the San Diego Freeway (405) south (605) south. Take the Artesia Freeway (91) Take Avalon Blvd. south to Victoria Street, turn toward Long Beach. Exit at the Vermont Avenue west toward Redondo Beach. Take the Central left. The entrance to campus is a right turn at off-ramp. Turn left (east) at the end of the off- Avenue exit and turn left; turn right onto Victoria Tamcliff Avenue. ramp onto 190th Street. -

SAN GABRIEL VALLEY Sb 1 Funding Subregional Overview Reducing Safer Emissions Fact Sheet Roads
YOUR STATE TRANSPORTATION DOLLARS AT WORK IN SAN GABRIEL VALLEY sb 1 funding subregional overview Reducing Safer Emissions Fact Sheet Roads Filling More > More safety improvements and Potholes expanding bike and pedestrian networks along the Glendora Urban Train and Greenway, Pasadena, Alhambra, Baldwin Park and Rosemead Funding for cities and unincorporated areas to: > More electric buses and expanded > Repair potholes and sidewalks bus routes for Arcadia, Claremont and Foothill Transit LA COUNTY > Install upgraded traffic signals and pedestrian lights > More active transportation projects State Investment to keep schools and students safer > Repave local streets in the Pasadena Unified School > Improve pedestrian and bike District $1 BILLION safety, and upgrade bus shelters > New safety and highway improvements for the SR-57/-60 PER YEAR Confluence and the SR-71 gap conversion projects Smoother Commutes Stretching your Measure M > Fixing overpasses and roads on Dollars the SR-60 freight corridor for truck safety > Improving traffic flow on the I-210, > Extending the Metro Gold Line from I-10 and SR-134, and repaving and Azusa to Montclair in partnership re-striping highways with San Bernardino County > Critical safety-enhancing grade Transportation Authority separations in Montebello and > Building a 17.3 mile dedicated Bus Industry/Rowland Heights Rapid Transit route that creates a > Operational and station connection between San Fernando improvements on the Metrolink Valley and San Gabriel Valley commuter rail system > Implementing “complete streets” > Funding for the Freeway Service pedestrian, road and bike safety Patrol to relieve congestion on improvements along Temple Av highways between Walnut and Pomona SAN GABRIEL VALLEY SUBREGION The state is investing approximately $1 billion per year in transportation funding in LA County from the new gas taxes and fees authorized by Senate Bill 1 (SB 1). -

Los Angeles Transportation Transit History – South LA
Los Angeles Transportation Transit History – South LA Matthew Barrett Metro Transportation Research Library, Archive & Public Records - metro.net/library Transportation Research Library & Archive • Originally the library of the Los • Transportation research library for Angeles Railway (1895-1945), employees, consultants, students, and intended to serve as both academics, other government public outreach and an agencies and the general public. employee resource. • Partner of the National • Repository of federally funded Transportation Library, member of transportation research starting Transportation Knowledge in 1971. Networks, and affiliate of the National Academies’ Transportation • Began computer cataloging into Research Board (TRB). OCLC’s World Catalog using Library of Congress Subject • Largest transit operator-owned Headings and honoring library, forth largest transportation interlibrary loan requests from library collection after U.C. outside institutions in 1978. Berkeley, Northwestern University and the U.S. DOT’s Volpe Center. • Archive of Los Angeles transit history from 1873-present. • Member of Getty/USC’s L.A. as Subject forum. Accessing the Library • Online: metro.net/library – Library Catalog librarycat.metro.net – Daily aggregated transportation news headlines: headlines.metroprimaryresources.info – Highlights of current and historical documents in our collection: metroprimaryresources.info – Photos: flickr.com/metrolibraryarchive – Film/Video: youtube/metrolibrarian – Social Media: facebook, twitter, tumblr, google+, -

Googledrive: an Interface to Google Drive
Package ‘googledrive’ July 8, 2021 Title An Interface to Google Drive Version 2.0.0 Description Manage Google Drive files from R. License MIT + file LICENSE URL https://googledrive.tidyverse.org, https://github.com/tidyverse/googledrive BugReports https://github.com/tidyverse/googledrive/issues Depends R (>= 3.3) Imports cli (>= 3.0.0), gargle (>= 1.2.0), glue (>= 1.4.2), httr, jsonlite, lifecycle, magrittr, pillar, purrr (>= 0.2.3), rlang (>= 0.4.9), tibble (>= 2.0.0), utils, uuid, vctrs (>= 0.3.0), withr Suggests covr, curl, downlit, dplyr (>= 1.0.0), knitr, mockr, rmarkdown, roxygen2, sodium, spelling, testthat (>= 3.0.0) VignetteBuilder knitr Config/Needs/website pkgdown, tidyverse, r-lib/downlit, tidyverse/tidytemplate Config/testthat/edition 3 Encoding UTF-8 Language en-US RoxygenNote 7.1.1.9001 NeedsCompilation no Author Lucy D'Agostino McGowan [aut], Jennifer Bryan [aut, cre] (<https://orcid.org/0000-0002-6983-2759>), RStudio [cph, fnd] Maintainer Jennifer Bryan <[email protected]> Repository CRAN Date/Publication 2021-07-08 09:10:06 UTC 1 2 R topics documented: R topics documented: as_dribble . .3 as_id . .4 as_shared_drive . .5 dribble . .6 dribble-checks . .6 drive_about . .7 drive_auth . .8 drive_auth_configure . 11 drive_browse . 12 drive_cp . 13 drive_create . 15 drive_deauth . 17 drive_download . 18 drive_empty_trash . 20 drive_endpoints . 20 drive_examples . 21 drive_extension . 22 drive_fields . 23 drive_find . 24 drive_get . 27 drive_has_token . 30 drive_link . 30 drive_ls . 31 drive_mime_type . 32 drive_mkdir . 33 drive_mv . 35 drive_publish . 37 drive_put . 38 drive_read_string . 40 drive_rename . 41 drive_reveal . 42 drive_rm . 45 drive_share . 46 drive_token . 48 drive_trash . 49 drive_update . 50 drive_upload . 51 drive_user . 54 googledrive-configuration . 55 request_generate . 57 request_make . 58 shared_drives . -

The Neighborly Substation the Neighborly Substation Electricity, Zoning, and Urban Design
MANHATTAN INSTITUTE CENTER FORTHE RETHINKING DEVELOPMENT NEIGHBORLY SUBstATION Hope Cohen 2008 er B ecem D THE NEIGHBORLY SUBstATION THE NEIGHBORLY SUBstATION Electricity, Zoning, and Urban Design Hope Cohen Deputy Director Center for Rethinking Development Manhattan Institute In 1879, the remarkable thing about Edison’s new lightbulb was that it didn’t burst into flames as soon as it was lit. That disposed of the first key problem of the electrical age: how to confine and tame electricity to the point where it could be usefully integrated into offices, homes, and every corner of daily life. Edison then designed and built six twenty-seven-ton, hundred-kilowatt “Jumbo” Engine-Driven Dynamos, deployed them in lower Manhattan, and the rest is history. “We will make electric light so cheap,” Edison promised, “that only the rich will be able to burn candles.” There was more taming to come first, however. An electrical fire caused by faulty wiring seriously FOREWORD damaged the library at one of Edison’s early installations—J. P. Morgan’s Madison Avenue brownstone. Fast-forward to the massive blackout of August 2003. Batteries and standby generators kicked in to keep trading alive on the New York Stock Exchange and the NASDAQ. But the Amex failed to open—it had backup generators for the trading-floor computers but depended on Consolidated Edison to cool them, so that they wouldn’t melt into puddles of silicon. Banks kept their ATM-control computers running at their central offices, but most of the ATMs themselves went dead. Cell-phone service deteriorated fast, because soaring call volumes quickly drained the cell- tower backup batteries. -

Heavy Duty Safety Switches 600 Volt Class H Fuse Provisions
Heavy Duty Safety Switches 600 Volt Class 3110 / Refer to Catalog 3100CT0901 ZZZVFKQHLGHUHOHFWULFXV Table 3.10: 600 Volts—Single Throw Fusible Horsepower Ratings c NEMA 4, 4X, 5 a 480 Vac 600 Vac 304 Stainless Steel NEMA 3R NEMA 12K NEMA 12, 3R b Max. Std. Max. NEMA 1 Rainproof (for 316 stainless, see With Knockouts Without Knockouts Std. page 3-7) Dust tight, (Using (Using (Using (Using System Amperes Indoor (Bolt-on Hubs, (Watertight Hubs, (Watertight Hubs, Dual Fast Dual dc e page 3-10) Watertight, Corrosion page 3-10) page 3-10) Fast Resistant Acting, Element, Acting, Element, (Watertight Hubs, page 3-10) Time One Time One Time Delay Time Delay Fuses) Fuses) Fuses) Fuses) Cat. No. $ Price Cat. No. $ Price Cat. No. $ Price Cat. No. $ Price Cat. No. $ Price 3Ø 3Ø 3Ø 3Ø 250 600 2-Wire (2 Blades and Fuseholders)—600 Vac, 600 Vdc 30 — — — ——— 60 Use three-wire devices — — — ——— 100 for two-wire applications — — — ——— 200 — — — ——— 400 H265 4206.00 H265R 5424.00 H265DS 14961.00 — — H265AWK 5025.00 100 d 250 d — — 50 50 600 H266 6653.00 H266R 10686.00 H266DS 21399.00 — — H266AWK 7341.00 150 d 400 d — — 50 50 800 H267 10365.00 H267R g 16385.00 — — — — H267AWK 15276.00 — — — — 50 50 1200 H268 14570.00 H268R g 17991.00 — — — — H268AWK 18044.00 — — — — 50 50 3-Wire (3 Blades and Fuseholders)—600 Vac, 600 Vdc e 30 H361 528.00 H361RB 899.00 H361DS 2520.00 H361A 1014.00 H361AWK 956.00 5 15 7-1/2 20 5 15 30 H361-2 f 617.00 H3612RB f 1049.00 — — H361-2A f 1035.00 H3612AWK f 977.00 5 15 7-1/2 20 — 15 60 H362 638.00 H362RB 1055.00 H362DS 2771.00 H362A -

1981 Caltrans Inventory of Pacific Electric Routes
1981 Inventory of PACIFIC ELECTRIC ROUTES I J..,. I ~ " HE 5428 . red by I58 ANGELES - DISTRICT 7 - PUBLIC TRANSPORTATION BRANCH rI P37 c.2 " ' archive 1981 INVENTORY OF PACIFIC ELECTRIC ROUTES • PREPARED BY CALIFORNIA DEPARTMENT OF TRANSPORTATION (CALTRANS) DISTRICT 07 PUBLIC TRANSPORTATION BRANCH FEBRUARY 1982 • TABLE OF CONTENTS PAGE I. EXECUTIVE SUMMARY 1 Pacific Electric Railway Company Map 3a Inventory Map 3b II. NQR'I'HIRN AND EASTERN DISTRICTS 4 A. San Bernardino Line 6 B. Monrovia-Glendora Line 14 C. Alhambra-San Gabriel Line 19 D. Pasadena Short Line 21 E. Pasadena Oak Knoll Line 23 F. Sierra Madre Line 25 G. South Pasadena Line 27 H. North Lake Avenue Line 30 10 North Fair Oaks Avenue Line 31 J. East Colorado Street Line 32 K. Pomona-Upland Line 34 L. San Bernardino-Riverside Line 36 M. Riverside-Corona Line 41 III. WESTERN DISTRICT 45 A. Glendale-Burbank Line 47 B. Hollywood Line Segment via Hill Street 52 C. South Hollywood-Sherman Line 55 D. Subway Hollywood Line 58 i TABLE OF CONTENTS (Contd. ) -PAGE III. WESTERN DISTRICT (Conta. ) E. San Fernando valley Line 61 F. Hollywood-Venice Line 68 o. Venice Short Line 71 H. Santa Monica via Sawtelle Line 76 I. westgate Line 80 J. Santa Monica Air Line 84 K. Soldier's Home Branch Line 93 L. Redondo Beach-Del Rey Line 96 M. Inglewood Line 102 IV. SOUTHIRN DISTRICT 106 A. Long Beach Line 108 B. American Avenue-North Long Beach Line 116 c. Newport-Balboa Line 118 D. E1 Segundo Line 123 E. San Pedro via Dominguez Line 129 F. -

History of El Sereno 1 Message
Richard Williams <[email protected]> History of El Sereno 1 message El Sereno Historical Society <[email protected]> Mon, Jun 24, 2013 at 2:02 PM To: Richard Williams <[email protected]> Hi Mr. Williams, please submit the attached PDF and this e-mail to Motion 11-2057 as a public comment. The attachment is a pdf copy of the researched History of El Sereno. This document is a respected, accurate, and well researched which is held as a reference by the Los Angeles City Public Library. This document provides accurate information on the History of El Sereno and contradicts the file that Anthony Manzano has submitted as the archived history of Rose Hills. A simple comparison of the two documents will show the difference between a well researched and accurate document, as is the history of El Sereno, to one that has superficial research and almost no evidence, such as the archived history of Rose Hills. It is also important to point out that although the front page of the archived history of Rose Hills states that it has been submitted to the Historical Society of Southern California for consideration and support in recognizing the community of Rose Hills, the archived history of Rose Hills has already been rejected by the Historical Society of Southern California for its lack of research and lack of supporting evidence. Thank you for your time. Regards, Jorge Garcia El Sereno Historical Society www.ElSereno90032.org Facebook Sow ing the Seeds of Know ledge Today; To Cultivate a Dynamic El Sereno Community Tomorrow El Sereno Official History-reset NO Color.pdf 17635K EL SERE}IO BR.t· . -

R-PUD Application Template
APPLICATION TO ESTABLISH A RESIDENTIAL GF#:___-___-___ PLANNED UNIT DEVELOPMENT MARSHALL COUNTY, IOWA To: The Marshall County Zoning Administrator. The undersigned is/are the owners of the property located in the unincorporated area of Marshall County, Iowa and request that the Zoning Administrator consider said property for establishment of a Residential Planned Unit Development: 911 Address of Property:______________________ Proposed Use:________________________ Current Zoning:___________________________ Proposed Zoning:________________________ The application fee to establish a 5-10 acre R-P.U.D. is $100.00, a 10-20 acre R-P.U.D. is $200.00, and a R-P.U.D. of more than 20 acres is $500.00 This fee is non-refundable. All submittals shall include the information listed in Article XI A, Section 12, Subsection A., (1-14) for items to be included on a preliminary residential planned unit development request. A site plan is required whenever an applicant asks for a change of zoning to either R-3, C-1, C-2 or F-P zoning. Requirements for a site plan are as stipulated in Article XVI of the Marshall County Zoning Ordinance No. 3. This application, the fee and the site plan (if necessary) are required to be submitted jointly. If any of these items are not included, it is considered an incomplete application and will not be accepted. The Marshall County R-PUD Review Staff will conduct a site review and will make comments on the application for the Zoning Commission and Board of Supervisors’ consideration. Please indicate if the property is involved -

Southeast Los Angeles County, CA Railroad and Goods Movement
Presented by: Michael Fischer, P.E. Cambridge Systematics In Association with: Jerry R. Wood, P.E. Director of Transportation and Engineering Gateway Cities Council of Governments Southeast Los Angeles County, CA Railroad and Goods Movement Southeast Los Angeles County, CA Railroad and Goods Movement Gateway Cities Council of Governments (GCCOG) Representing People in a Prime Goods Movement Area • Sub-regional agency of Southeast Los Angeles County, CA representing 27 cities, unincorporated portions of Los Angeles County and the Port of Long Beach (2.2 million residents.) • Located landside of the Ports of Long Beach and Los Angeles, the largest port complex in the U.S. (and 5th largest in the world.) • About 40% of nations imports enter U.S. through these two ports – volumes could grow from 12-13M TEUs (current) to maximum of 43M (2035-2040) • I-710 Freeway is primary port access route -- highest truck-related accident rates in the state and no permanent, operating truck inspection facilities in the GCCOG area. • This area has the highest concentration of freight train, tracks and warehouse and distribution centers in the country. 2 Southeast Los Angeles County, CA Railroad and Goods Movement • GCCOG Boundaries and Cities • Southeast & East L.A. County, CA Downtown L.A. GCCOG Ports of Long Beach & Los Angeles 3 Southeast Los Angeles County, CA Railroad and Goods Movement Economics Analysis of Ports • The two ports handle 40-45% of the nation’s imported goods (by some estimates, 25% to local markets and 75% for national distribution)