In Spherical Geometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Proofs with Perpendicular Lines
3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units. -

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

Using Non-Euclidean Geometry to Teach Euclidean Geometry to K–12 Teachers
Using non-Euclidean Geometry to teach Euclidean Geometry to K–12 teachers David Damcke Department of Mathematics, University of Portland, Portland, OR 97203 [email protected] Tevian Dray Department of Mathematics, Oregon State University, Corvallis, OR 97331 [email protected] Maria Fung Mathematics Department, Western Oregon University, Monmouth, OR 97361 [email protected] Dianne Hart Department of Mathematics, Oregon State University, Corvallis, OR 97331 [email protected] Lyn Riverstone Department of Mathematics, Oregon State University, Corvallis, OR 97331 [email protected] January 22, 2008 Abstract The Oregon Mathematics Leadership Institute (OMLI) is an NSF-funded partner- ship aimed at increasing mathematics achievement of students in partner K–12 schools through the creation of sustainable leadership capacity. OMLI’s 3-week summer in- stitute offers content and leadership courses for in-service teachers. We report here on one of the content courses, entitled Comparing Different Geometries, which en- hances teachers’ understanding of the (Euclidean) geometry in the K–12 curriculum by studying two non-Euclidean geometries: taxicab geometry and spherical geometry. By confronting teachers from mixed grade levels with unfamiliar material, while mod- eling protocol-based pedagogy intended to emphasize a cooperative, risk-free learning environment, teachers gain both content knowledge and insight into the teaching of mathematical thinking. Keywords: Cooperative groups, Euclidean geometry, K–12 teachers, Norms and protocols, Rich mathematical tasks, Spherical geometry, Taxicab geometry 1 1 Introduction The Oregon Mathematics Leadership Institute (OMLI) is a Mathematics/Science Partner- ship aimed at increasing mathematics achievement of K–12 students by providing professional development opportunities for in-service teachers. -

And Are Lines on Sphere B That Contain Point Q
11-5 Spherical Geometry Name each of the following on sphere B. 3. a triangle SOLUTION: are examples of triangles on sphere B. 1. two lines containing point Q SOLUTION: and are lines on sphere B that contain point Q. ANSWER: 4. two segments on the same great circle SOLUTION: are segments on the same great circle. ANSWER: and 2. a segment containing point L SOLUTION: is a segment on sphere B that contains point L. ANSWER: SPORTS Determine whether figure X on each of the spheres shown is a line in spherical geometry. 5. Refer to the image on Page 829. SOLUTION: Notice that figure X does not go through the pole of ANSWER: the sphere. Therefore, figure X is not a great circle and so not a line in spherical geometry. ANSWER: no eSolutions Manual - Powered by Cognero Page 1 11-5 Spherical Geometry 6. Refer to the image on Page 829. 8. Perpendicular lines intersect at one point. SOLUTION: SOLUTION: Notice that the figure X passes through the center of Perpendicular great circles intersect at two points. the ball and is a great circle, so it is a line in spherical geometry. ANSWER: yes ANSWER: PERSEVERANC Determine whether the Perpendicular great circles intersect at two points. following postulate or property of plane Euclidean geometry has a corresponding Name two lines containing point M, a segment statement in spherical geometry. If so, write the containing point S, and a triangle in each of the corresponding statement. If not, explain your following spheres. reasoning. 7. The points on any line or line segment can be put into one-to-one correspondence with real numbers. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -

On the Standard Lengths of Angle Bisectors and the Angle Bisector Theorem
Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, pp.15-27 ON THE STANDARD LENGTHS OF ANGLE BISECTORS AND THE ANGLE BISECTOR THEOREM G.W INDIKA SHAMEERA AMARASINGHE ABSTRACT. In this paper the author unveils several alternative proofs for the standard lengths of Angle Bisectors and Angle Bisector Theorem in any triangle, along with some new useful derivatives of them. 2010 Mathematical Subject Classification: 97G40 Keywords and phrases: Angle Bisector theorem, Parallel lines, Pythagoras Theorem, Similar triangles. 1. INTRODUCTION In this paper the author introduces alternative proofs for the standard length of An- gle Bisectors and the Angle Bisector Theorem in classical Euclidean Plane Geometry, on a concise elementary format while promoting the significance of them by acquainting some prominent generalized side length ratios within any two distinct triangles existed with some certain correlations of their corresponding angles, as new lemmas. Within this paper 8 new alternative proofs are exposed by the author on the angle bisection, 3 new proofs each for the lengths of the Angle Bisectors by various perspectives with also 5 new proofs for the Angle Bisector Theorem. 1.1. The Standard Length of the Angle Bisector Date: 1 February 2012 . 15 G.W Indika Shameera Amarasinghe The length of the angle bisector of a standard triangle such as AD in figure 1.1 is AD2 = AB · AC − BD · DC, or AD2 = bc 1 − (a2/(b + c)2) according to the standard notation of a triangle as it was initially proved by an extension of the angle bisector up to the circumcircle of the triangle. -

Geometry: Euclid and Beyond, by Robin Hartshorne, Springer-Verlag, New York, 2000, Xi+526 Pp., $49.95, ISBN 0-387-98650-2
BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 39, Number 4, Pages 563{571 S 0273-0979(02)00949-7 Article electronically published on July 9, 2002 Geometry: Euclid and beyond, by Robin Hartshorne, Springer-Verlag, New York, 2000, xi+526 pp., $49.95, ISBN 0-387-98650-2 1. Introduction The first geometers were men and women who reflected on their experiences while doing such activities as building small shelters and bridges, making pots, weaving cloth, building altars, designing decorations, or gazing into the heavens for portentous signs or navigational aides. Main aspects of geometry emerged from three strands of early human activity that seem to have occurred in most cultures: art/patterns, navigation/stargazing, and building structures. These strands developed more or less independently into varying studies and practices that eventually were woven into what we now call geometry. Art/Patterns: To produce decorations for their weaving, pottery, and other objects, early artists experimented with symmetries and repeating patterns. Later the study of symmetries of patterns led to tilings, group theory, crystallography, finite geometries, and in modern times to security codes and digital picture com- pactifications. Early artists also explored various methods of representing existing objects and living things. These explorations led to the study of perspective and then projective geometry and descriptive geometry, and (in the 20th century) to computer-aided graphics, the study of computer vision in robotics, and computer- generated movies (for example, Toy Story ). Navigation/Stargazing: For astrological, religious, agricultural, and other purposes, ancient humans attempted to understand the movement of heavenly bod- ies (stars, planets, Sun, and Moon) in the apparently hemispherical sky. -

Project 2: Euclidean & Spherical Geometry Applied to Course Topics
Project 2: Euclidean & Spherical Geometry Applied to Course Topics You may work alone or with one other person. During class you will write down your top problems (unranked) and from this you will be assigned one problem. In this project, we will use intuition from previous Euclidean geometry knowledge along with experiences from hands-on models and/or research. The purpose of this assignment is an introduction to the concepts in the course syllabus as we explore diverse geometric perspectives. Project Components: a) Review content related to your problem that applies to the geometry of the plane / Euclidean geometry / flat geometry. For example, if you have Problem 1 then you might review the definitions of lines and how to calculate them, for Problem 9 you might review some information related to area and surface area, for Problem 10 you might review coordinate systems... You may use our book, the internet, or other sources. b) Why the topic is important in mathematics and the real-world? Conduct searches like \trian- gles are important" or a search word related to your problem and then (with and without quotations) words like important, interesting, useful, or real-life applications. You might also pick some specific fields to see if there are applications such as: Pythagorean theorem chemistry c) Summarize diverse spherical perspectives. You do not need to prove an answer or completely resolve the issue on the sphere. You should look for various perspectives related to spherical geometry, and summarize those in your own words. Try different combinations of search terms related to your problem along with words like sphere, spherical, earth, or spherical geometry. -

Advanced Euclidean Geometry
Advanced Euclidean Geometry Paul Yiu Summer 2016 Department of Mathematics Florida Atlantic University July 18, 2016 Summer 2016 Contents 1 Some Basic Theorems 101 1.1 The Pythagorean Theorem . ............................ 101 1.2 Constructions of geometric mean . ........................ 104 1.3 The golden ratio . .......................... 106 1.3.1 The regular pentagon . ............................ 106 1.4 Basic construction principles ............................ 108 1.4.1 Perpendicular bisector locus . ....................... 108 1.4.2 Angle bisector locus . ............................ 109 1.4.3 Tangency of circles . ......................... 110 1.4.4 Construction of tangents of a circle . ............... 110 1.5 The intersecting chords theorem ........................... 112 1.6 Ptolemy’s theorem . ................................. 114 2 The laws of sines and cosines 115 2.1 The law of sines . ................................ 115 2.2 The orthocenter ................................... 116 2.3 The law of cosines .................................. 117 2.4 The centroid ..................................... 120 2.5 The angle bisector theorem . ............................ 121 2.5.1 The lengths of the bisectors . ........................ 121 2.6 The circle of Apollonius . ............................ 123 3 The tritangent circles 125 3.1 The incircle ..................................... 125 3.2 Euler’s formula . ................................ 128 3.3 Steiner’s porism ................................... 129 3.4 The excircles .................................... -

4 3 E B a C F 2
See-Saw Geometry and the Method of Mass-Points1 Bobby Hanson February 27, 2008 Give me a place to stand on, and I can move the Earth. — Archimedes. 1. Motivating Problems Today we are going to explore a kind of geometry similar to regular Euclidean Geometry, involving points and lines and triangles, etc. The main difference that we will see is that we are going to give mass to the points in our geometry. We will call such a geometry, See-Saw Geometry (we’ll understand why, shortly). Before going into the details of See-Saw Geometry, let’s look at some problems that might be solved using this different geometry. Note that these problems are perfectly solvable using regular Euclidean Geometry, but we will find See-Saw Geometry to be very fast and effective. Problem 1. Below is the triangle △ABC. Side BC is divided by D in a ratio of 5 : 2, and AB is divided by E in a ration of 3 : 4. Find the ratios in which F divides the line segments AD and CE; i.e., find AF : F D and CF : F E. (Note: in Figure 1, below, only the ratios are shown; the actual lengths are unknown). B 3 E 5 4 F D 2 A C Figure 1 1My notes are shamelessly stolen from notes by Tom Rike, of the Berkeley Math Circle available at http://mathcircle.berkeley.edu/archivedocs/2007 2008/lectures/0708lecturespdf/MassPointsBMC07.pdf . 1 2 Problem 2. In Figure 2, below, D and E divide sides BC and AB, respectively, as before. -

Spherical Geometry
987023 2473 < % 52873 52 59 3 1273 ¼4 14 578 2 49873 3 4 7∆��≌ ≠ 3 δ � 2 1 2 7 5 8 4 3 23 5 1 ⅓β ⅝Υ � VCAA-AMSI maths modules 5 1 85 34 5 45 83 8 8 3 12 5 = 2 38 95 123 7 3 7 8 x 3 309 �Υβ⅓⅝ 2 8 13 2 3 3 4 1 8 2 0 9 756 73 < 1 348 2 5 1 0 7 4 9 9 38 5 8 7 1 5 812 2 8 8 ХФУШ 7 δ 4 x ≠ 9 3 ЩЫ � Ѕ � Ђ 4 � ≌ = ⅙ Ё ∆ ⊚ ϟϝ 7 0 Ϛ ό ¼ 2 ύҖ 3 3 Ҧδ 2 4 Ѽ 3 5 ᴂԅ 3 3 Ӡ ⍰1 ⋓ ӓ 2 7 ӕ 7 ⟼ ⍬ 9 3 8 Ӂ 0 ⤍ 8 9 Ҷ 5 2 ⋟ ҵ 4 8 ⤮ 9 ӛ 5 ₴ 9 4 5 € 4 ₦ € 9 7 3 ⅘ 3 ⅔ 8 2 2 0 3 1 ℨ 3 ℶ 3 0 ℜ 9 2 ⅈ 9 ↄ 7 ⅞ 7 8 5 2 ∭ 8 1 8 2 4 5 6 3 3 9 8 3 8 1 3 2 4 1 85 5 4 3 Ӡ 7 5 ԅ 5 1 ᴂ - 4 �Υβ⅓⅝ 0 Ѽ 8 3 7 Ҧ 6 2 3 Җ 3 ύ 4 4 0 Ω 2 = - Å 8 € ℭ 6 9 x ℗ 0 2 1 7 ℋ 8 ℤ 0 ∬ - √ 1 ∜ ∱ 5 ≄ 7 A guide for teachers – Years 11 and 12 ∾ 3 ⋞ 4 ⋃ 8 6 ⑦ 9 ∭ ⋟ 5 ⤍ ⅞ Geometry ↄ ⟼ ⅈ ⤮ ℜ ℶ ⍬ ₦ ⍰ ℨ Spherical Geometry ₴ € ⋓ ⊚ ⅙ ӛ ⋟ ⑦ ⋃ Ϛ ό ⋞ 5 ∾ 8 ≄ ∱ 3 ∜ 8 7 √ 3 6 ∬ ℤ ҵ 4 Ҷ Ӂ ύ ӕ Җ ӓ Ӡ Ҧ ԅ Ѽ ᴂ 8 7 5 6 Years DRAFT 11&12 DRAFT Spherical Geometry – A guide for teachers (Years 11–12) Andrew Stewart, Presbyterian Ladies’ College, Melbourne Illustrations and web design: Catherine Tan © VCAA and The University of Melbourne on behalf of AMSI 2015. -
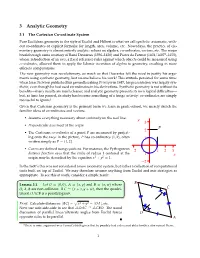
3 Analytic Geometry
3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2).