Shoreline Change Rate Estimation and Its Forecast: Remote Sensing, Geographical Information System and Statistics-Based Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Problems of Salination of Land in Coastal Areas of India and Suitable Protection Measures
Government of India Ministry of Water Resources, River Development & Ganga Rejuvenation A report on Problems of Salination of Land in Coastal Areas of India and Suitable Protection Measures Hydrological Studies Organization Central Water Commission New Delhi July, 2017 'qffif ~ "1~~ cg'il'( ~ \jf"(>f 3mft1T Narendra Kumar \jf"(>f -«mur~' ;:rcft fctq;m 3tR 1'j1n WefOT q?II cl<l 3re2iM q;a:m ~0 315 ('G),~ '1cA ~ ~ tf~q, 1{ffit tf'(Chl '( 3TR. cfi. ~. ~ ~-110066 Chairman Government of India Central Water Commission & Ex-Officio Secretary to the Govt. of India Ministry of Water Resources, River Development and Ganga Rejuvenation Room No. 315 (S), Sewa Bhawan R. K. Puram, New Delhi-110066 FOREWORD Salinity is a significant challenge and poses risks to sustainable development of Coastal regions of India. If left unmanaged, salinity has serious implications for water quality, biodiversity, agricultural productivity, supply of water for critical human needs and industry and the longevity of infrastructure. The Coastal Salinity has become a persistent problem due to ingress of the sea water inland. This is the most significant environmental and economical challenge and needs immediate attention. The coastal areas are more susceptible as these are pockets of development in the country. Most of the trade happens in the coastal areas which lead to extensive migration in the coastal areas. This led to the depletion of the coastal fresh water resources. Digging more and more deeper wells has led to the ingress of sea water into the fresh water aquifers turning them saline. The rainfall patterns, water resources, geology/hydro-geology vary from region to region along the coastal belt. -

Draft Initial Environmental Examination
Initial Environmental Examination Document stage: Draft for Consultation Project Number: 43253-027 May 2018 IND: Karnataka Integrated Urban Water Management Investment Program (Tranche 2) – Improvements for 24 x 7 Water Supply System for Town Municipal Council in Kundapura Package No. 02KDP01 Prepared by Karnataka Urban Infrastructure Development and Finance Corporation, Government of Karnataka for the Asian Development Bank. CURRENCY EQUIVALENTS (as of 11 May 2018) Currency unit – Indian rupee (₹) ₹1.00 = $0.0149 $1.00 = ₹67.090 ABBREVIATIONS ADB – Asian Development Bank CFE – consent for establishment CFO – consent for operation CGWB – Central Ground Water Board CPCB – Central Pollution Control Board CRZ – Coastal Regulation Zone DLIC – District Level Implementation Committee EHS – Environmental, Health and Safety EIA – environmental impact assessment EMP – environmental management plan GRC – grievance redress committee GRM – grievance redress mechanism HSC – house service connection H&S – health and safety IEE – initial environmental examination IFC – International Finance Corporation KCZMA – Karnataka Coastal Zone Management Authority KIUWMIP – Karnataka Integrated Urban Water Management Investment Program KSPCB – Karnataka State Pollution Control Board KUDCEMP – Karnataka Urban Development and Costal Environmental Management Project KUIDFC – Karnataka Urban Infrastructure Development and Finance Corporation MoEFCC – Ministry of Environment, Forest and Climate Change NGO – nongovernment organization OHT – overhead tank O&M – operation -

Integrated Coastal Zone Management Plan for Udupi Coast Using Remote Sensing, Geographical Information System and Global Position System
Journal of Applied Remote Sensing, Vol. 2, 023515 (14 April 2008) Integrated coastal zone management plan for Udupi coast using remote sensing, geographical information system and global position system G. S. Dwarakish,a S. A. Vinay,b S. M. Dinakar,c Jagadeesha B. Pai,d K. Mahaganesha,e and Usha Natesanf a Asst. Professor, Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal, Srinivasnagar. P. O. 575 025, India. [email protected], [email protected] b P.G. Student, Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal, Srinivasnagar. P. O. 575 025, India. [email protected] c Research Assistant, Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal, Srinivasnagar. P. O. 575 025, India. [email protected] d Research Scholar, Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal, Srinivasnagar. P. O. 575 025, India. [email protected] e Research Scholar, Department of Applied Mechanics and Hydraulics, National Institute of Technology Karnataka, Surathkal, Srinivasnagar. P. O. 575 025, India. [email protected] f Asst. Professor, Centre for Environmental Studies, Anna University, Chennai- 600 025, India. [email protected] Abstract: Coastal areas are under great pressure due to increase in human population and industrialization/commercialization and hence these areas are vulnerable to environmental degradation, resource reduction and user conflicts. In the present study an Integrated Coastal Zone Management Plan (ICZMP) has been developed for Udupi Coast in Karnataka, along West Coast of India. The various data products used in the present study includes IRS-1C LISS-III + PAN and IRS-P6 LISS III remotely sensed data, Naval Hydrographic Charts and Survey of India (SOI) toposheets, in addition to ground truth data. -

District Disaster Management Plan- Udupi
DISTRICT DISASTER MANAGEMENT PLAN- UDUPI UDUPI DISTRICT 2015-16 -1- -2- Executive Summary The District Disaster Management Plan is a key part of an emergency management. It will play a significant role to address the unexpected disasters that occur in the district effectively. The information available in DDMP is valuable in terms of its use during disaster. Based on the history of various disasters that occur in the district, the plan has been so designed as an action plan rather than a resource book. Utmost attention has been paid to make it handy, precise rather than bulky one. This plan has been prepared which is based on the guidelines from the National Institute of Disaster Management (NIDM). While preparing this plan, most of the issues, relevant to crisis management, have been carefully dealt with. During the time of disaster there will be a delay before outside help arrives. At first, self-help is essential and depends on a prepared community which is alert and informed. Efforts have been made to collect and develop this plan to make it more applicable and effective to handle any type of disaster. The DDMP developed touch upon some significant issues like Incident Command System (ICS), In fact, the response mechanism, an important part of the plan is designed with the ICS. It is obvious that the ICS, a good model of crisis management has been included in the response part for the first time. It has been the most significant tool for the response manager to deal with the crisis within the limited period and to make optimum use of the available resources. -

Coastal Zone Environmental Management in Udupi District, Karnataka State, India
RESEARCH INVENTY: International Journal of Engineering and Science ISSN: 2278-4721, Vol. 1, Issue 3 (Sept 2012), PP 08-11 www.researchinventy.com Coastal Zone Environmental Management in Udupi District, Karnataka State, India 1. 2 3 Dodda Aswathanarayana Swamy, .Dr.B.E.Basavarajappa, .Prof.E.T.Puttaiah, Research Scholar 1Dept. of PG Studies & Research in Environmental Science, Kuvempu University Shankaraghatta-577451, Karnataka State 2Professor, Department of Chemistry, Bapuji Institute of Engineering and Technology, Davangere, Karnataka State, India 3Professor, Department of Environmental Science, Kuvempu University Shankaraghatta-577451, Karnataka State, India Abstract: The Udupi coastal zone represents varied and highly productive ecosystems such as mangroves, coral reefs and sand dunes. These ecosystems are under pressure on account of increased anthropogenic activities such as discharge of industrial and municipal sewage, land use, tourism, maritime transport, dumping at sea degrade the coast. It is necessary to protect these coastal ecosystems to ensure sustainable development. This requires information on habitats, landforms, coastal processes, water quality, natural hazards on a repetitive basis. The Coastal zone environmental management plan tool is also required for protection of environmental components. I. Introduction. Karnataka’s coast stretches for 320 kilometres along the three districts of Dakshina Kannada, Udupi and Uttara Kannada. Of these, Uttara Kannada has 160-kilometre long coastline while 98 kilometres are in Udupi district and the rest in Dakshina Kannada. It’s three distinct agro-climatic zones range from coastal flatlands in the west with undulating hills and valleys in the middle and high hill ranges in the east that separates it from the peninsula. There is a narrow strip of coastal plains with varying width between the mountain and the Arabian Sea, the average width being about 20 km. -

GI Journal No. 77 1 November 30, 2015
GI Journal No. 77 1 November 30, 2015 GOVERNMENT OF INDIA GEOGRAPHICAL INDICATIONS JOURNAL NO.77 NOVEMBER 30, 2015 / AGRAHAYANA 09, SAKA 1936 GI Journal No. 77 2 November 30, 2015 INDEX S. No. Particulars Page No. 1 Official Notices 4 2 New G.I Application Details 5 3 Public Notice 6 4 GI Applications Guledgudd Khana - GI Application No.210 7 Udupi Sarees - GI Application No.224 16 Rajkot Patola - GI Application No.380 26 Kuthampally Dhoties & Set Mundu - GI Application No.402 37 Waghya Ghevada - GI Application No.476 47 Navapur Tur Dal - GI Application No.477 53 Vengurla Cashew - GI Application No.489 59 Lasalgaon Onion - GI Application No.491 68 Maddalam of Palakkad (Logo) - GI Application No.516 76 Brass Broidered Coconut Shell Craft of Kerala (Logo) - GI 81 Application No.517 Screw Pine Craft of Kerala (Logo) - GI Application No.518 89 6 General Information 94 7 Registration Process 96 GI Journal No. 77 3 November 30, 2015 OFFICIAL NOTICES Sub: Notice is given under Rule 41(1) of Geographical Indications of Goods (Registration & Protection) Rules, 2002. 1. As per the requirement of Rule 41(1) it is informed that the issue of Journal 77 of the Geographical Indications Journal dated 30th November 2015 / Agrahayana 09th, Saka 1936 has been made available to the public from 30th November 2015. GI Journal No. 77 4 November 30, 2015 NEW G.I APPLICATION DETAILS App.No. Geographical Indications Class Goods 530 Tulaipanji Rice 31 Agricultural 531 Gobindobhog Rice 31 Agricultural 532 Mysore Silk 24, 25 and 26 Handicraft 533 Banglar Rasogolla 30 Food Stuffs 534 Lamphun Brocade Thai Silk 24 Textiles GI Journal No. -

20/10/2020 Government of Karnataka Page:363
20/10/2020 GOVERNMENT OF KARNATAKA PAGE:363 DEPARTMENT OF PRE UNIVERSITY EDUCATION LIST OF PU COLLEGES IN UDUPI DISTRICT AS ON 20/10/2020 ******************************************************************************** SLNO COLCD NAME AND ADDRESS YEAR OF OPEN & COLL TYPE OPENING & AIDED GO NOS. WITH DATE ******************************************************************************** 4882 SU0012 GOVT PU COLLEGE 71-72 GOVT PU COL PALIMAR ED 40 SLB 70 DT 30-04-1971 UDUPI TQ 574112 -------------------------------------------------------------------------------- 4883 SU0013 GOVT PU COLLEGE GOVT PU COL HEJAMADI UDUPI TQ 574103 -------------------------------------------------------------------------------- 4884 SU0021 POORNAPRAJNA PU COLLEGE 60-61 BIFUR PU COL UDUPI 576101 -------------------------------------------------------------------------------- 4885 SU0023 SVS PU COLLEGE 72-73 AIDED PU COL KATAPADI ED 19 TPU 72 DT 16-05-1972 UDUPI TQ 574105 ED 43 UDC 71 DT 07/08/1972 -------------------------------------------------------------------------------- 4886 SU0024 MAHATMAGANDHI MEMO PU COL 49-50 BIFUR PU COL UDUPI ROP 44 DZ 7/50-51 DT 5-10-1950 576102 -------------------------------------------------------------------------------- 4887 SU0025 GOVT PU COLLEGE 72-73 GOVT PU COL HIRIADKA UDUPI TQ 576113 -------------------------------------------------------------------------------- 4888 SU0026 MANIPAL PU COLLEGE 72-73 AIDED PU COL VIDYANAGAR MANIPAL ED 43 UDC 71 DT 07-08-1972 UDUPI TQ 576119 ED 43 UDC 71 DT 07/08/1972 -------------------------------------------------------------------------------- -

District Census Handbook, Dakshina, Part XII-A, Series-11
CENSUS OF INDIA 1991 Series -11 KARNATAKA DISTRICT CENSUS HANDBOOK DAKSHINA KANNADA DISTRICT PART XII - A VILLAGE AND TOWN DIRECTORY SOBHA NAMBISAN Director of Census Operations. Karnataka CONTENTS Page No. FOREWORD v-vi PREFACE vii-viii IMPORTANT STATISTICS xi-xiv ANALYTICAL NOTE xv-xliv Section,·I • Village Directory Explanatory Notc 1-9 Alphabetical List of Villages - Bantval C.O.Block 13-15 Village Directory Statement - Bantvill C.O.Block 16-33 Alphabetical List of Villages - Beltangadi C.O.Block 37-39 Village Directory Statement - Bcltangadi C.D.Block 40-63 Alphabetical List of Villages - Karkal C.D.Block 67-69 Village Directory Statement - Karkal C.D.Block 70-91 Alphabetical List of Villages - Kundapura C.O.Block 95-97 Village Directory Statement - Kundapur C.O.Block 98-119 Alphabetical List of Villages • Mangalore C.O.Block 123-124 Village Directory Statement - Mangalorc C.D.Block 126-137 Alphabetical List of Villages - PuHur C.D.Block 141-142 Village Directory Statement - Pullur C.D.Block 144-155 Alphabetical List of Villages - Sulya C.O.Block 159-160 Village Directory Statement - Sulya C.D.Block 162-171 Alphabetical List of Villages - Udupi C.D.Block 175-177 Village Directory Statement - Udupi C.D.Block 178-203 Appendix I!"IV • I Community Devclopment Blockwise Abstract for Educational, Medical and Other Amenities 206-209 II Land Utilisation Data in respect of Non-Municipal Census Towns 208-209 III List of Villages where no amenities except Drinking Water arc available 210 IV-A List of Villages according to the proportion of Scheduled Castes to Total Population by Ranges 211-216 IV-B List of Villages according to the proportion of Scheduled Tribes to Total Population by Ranges 217-222 (iii) Section-II - Town Din'ctory Explanatory Note 225-21:; Statement . -

July 2021.Pmd
MANGALORE TODAY - SEPTEMBER 2021 1 2 MANGALORE TODAY - SEPTEMBER 2021 PPPOWER POINT PICTURE OF THE MONTH Hands-on Experience! Union Minister of State for Agriculture and Farmers' Welfare Shobha Karandlaje joins farmers in cultivating a fallow land at Kadekar village in Udupi as part of Hadilu Bhoomi Revival Scheme. ““““““ WWWORDSWORTH ”””””” “We must break the walls of “The musical world has caste, religion, superstitions the immense power to as well as mistrust that attract lakhs of people as create impediments in the music plays a very key role path of our progress” in enlivening our minds Prof Sabeeha B.Gowda, Professor, Dept of and hearts” Kannada Studies of Mangalore University at noted singer Ajay Warrior at the inaurual of a farewell ceremony on the occasion of her “Knowledge of local Karavali Music Camp in Mangaluru. retirement from service. languages will go a long way in assisting the police “Ranga Mandiras need to be “Man can lead a peaceful to efficiently maintain law protected if we have to life when he incorporates and order as well as in preserve and promote the good values and shuns his investigation of crimes” theatrical field” ego” City Police Commissioner N Shashi eminent Kannada movie director Rajendra Prof. P S Yadapadittaya, Vice Chancellor of Kumar at the inaugural of the month Singh Babu while launching the fund raising Mangalore University at the Kanaka lecture long Tulu learning workshop for police drive for the renovation of Don Bosco Hall in series at the University. officers and personnel. Mangaluru. MANGALORE TODAY - SEPTEMBER 2021 3 EEEDITOR’’’SSS EDGE VOL 24 ISSUE 7 SEPTEMBER 2021 Publisher and Editor V. -
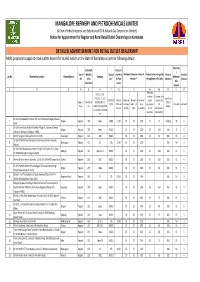
Final for Advertisement.Xlsx
MANGALORE REFINERY AND PETROCHEMICALS LIMITED (A Govt of India Enterprise and Subsidiary of Oil & Natural Gas Corporation Limited) Notice for Appointment for Regular and Rural Retail Outlet Dealerships in Karnataka DETAILED ADVERTISEMENT FOR RETAIL OUTLET DEALERSHIP MRPL proposes to appoint retail outlets dealers for its HiQ outlets in the State of Karnataka as per the following details: Fixed Fee Estimated Rent per / Type of Monthly Type of month in Minimum Dimension /Area of Finance to be arranged by Mode of Security Loc.No Name of the Location Revnue District Category Minimum RO Sales Site* Rs.P per the site ** the applicant in Rs Lakhs Selection Deposit Bid Potential # Sq.mt amount 1 2 3 4 5 6 7 7A 8 9a 9b 10 11 12 Estimated SC/SC CC-1/SC working Estimated fund PH/ST/ST CC-1/ST Draw of Lots CODO/DOD Only for Minimum Minimum Minimum capital required for Regular / MS+HSD in PH/OBC/OBC CC- (DOL) / O/CFS CODO and Frontage Depth (in Area requirement RO in Rs Lakhs in Rs Lakhs Rural KLs 1/OBC PH/OPEN/OPEN Bidding CFS sites (in Mts) Mts) (in Sq.Mts) for RO infrastructure CC-1/OPEN CC-2/OPEN operation development PH On LHS From Mezban Function Hall To Indal Circle On Belgavi Bauxite 1 Belgavi Regular 240 Open CODO 51.00 20 20 600 25 15 Bidding 30 5 Road On LHS From Kerala Hotel In Biranholi Village To Hanuman Temple 2 Belgavi Regular 230 Open DODO - 35 35 1225 25 100 DOL 15 5 ,Ukkad On Kolhapur To Belgavi - NH48 3 Within Tanigere Panchayath Limit On SH 76 Davangere Regular 105 OBC DODO - 30 30 900 25 75 DOL 15 4 On LHS Of NH275 From Byrapatna (Channapatna Taluk) Towards 4 Ramnagara Regular 171 SC CFS 22.90 35 35 1225 - - DOL Nil 3 Mysore On LHS From Sharanabasaveshwar Temple To St Xaviers P U College 5 Kalburgi Regular 225 Open CC-1 DODO - 35 35 1225 25 100 DOL 15 5 On NH50 (Kalburgi To Vijaypura Road) 6 Within 02 Kms From Km Stone No. -

CENTRE for DISTANCE EDUCATION I M.Com 2018-19 Register No
MANGALORE UNIVERSITY CENTRE FOR DISTANCE EDUCATION I M.com 2018-19 Register No. Candidate Name Gender Email Mobile Caste Address DDNO Date Amount Category CHAITHRA 2 chaithrara996@g 7204941233 GM Sri Raj Nivas, Arya Samaj Road, 2nd 2282 05.10.2018 6900 mail.com Cross, Balmatta, Mangalore - 575 003 1 ASHWINI T 2 9844373336 GM Thotanthila House, Alankar Post & Village, 1961 26.09.2018 6900 Puttur Tq, D.K - 574 285 2 SHRUTHI C H 2 9400228657 GM Chennumoole House, P.O Vaninagar, 1955 26.09.2018 6900 Kasaragod Dist, Kerala - 671 552 3 MANASA 2 manasaalekki@g 9741139717 GM Alekki House, Kaniyoor Post & Village, 1967 26.09.2018 6900 mail.com Belthangady Tq - 574 217 4 RADHIKA KUMARI 2 radhikar845@gm 7899966039 GM D/o Mahabala, Hulimane Kirimanjeshwara, 1872 25.09.2018 6900 ail.com Kundapura - 576 219 5 PANCHAMI R D 2 panchamird789@ 9071876554 GM D/o Radha Krishna D., E-1 Block, D.No. 003560 26.09.2018 6900 gmail.com 102, KSRP Police Quartes, Assaigoli, 6 Konaje, Mangalore, D.K - 574 199 SUPRIYA 2 supriyagowda@g 7353712756 / GM Kawate House, Laila Post & Village, 003546 26.09.2018 6900 mail.com 9945991879 Belthangady Tq, D.K - 574214 7 HARINAKSHI P L 2 harini106@gmail. 7025001705 ST Payaradka House, Samekochi Post, 1957 26.09.2018 6900 com Chengala Via, Kasaragod Dist, Kerala - 671 8 541 WENSON ROLLEN PINTO 2 wensonpinto1@g 9902632498 GM Christha Kiran, Iruvail Road, Thodar Post, 3125 29.10.2018 6900 mail.com Masthikatte, Moodbidri - 574 227 9 SHOBHITHA 2 shobhitha.udy@g 7619637856 GM Padala House, Uppinangady Post & 3169 16.11.2018 6900 mail.com Village, Puttur Tq, D.K - 574 241 10 SUSHMITHA 2 sushmithahedrala 9686310478 GM D/o B Sundara Acharya, Bedrala Nekkare 2795 15.11.2018 6900 @gmail.com House, Chikkamudnoor Post & Village, 11 Puttur Tq, D.K - 574 203 M TAUSIF 1 tausifspete@gma 9972361344 GM Ashraf Manzil, D.No. -

District Census Handbook, Udupi, Part XII-A & B, Series-30
CENSUS OF INDIA 2001 SERIES - 30 KARNATAKA PART XII - A & B : VILLAGE AND TOWN DIRECTORY & PRIMARY CENSUS ABSTRACT DISTRICT CENSUS HANDBOOK UDUPI DIRECTORATE OF CENSUS OPERATIONS, KARNATAKA,BANGALORE MOT -DMrid Stt~'$ 'Silhrurrull ii:s lkorcm1lJ.orll Ime4llf ~ ;a :sJImlllll w!IniirdIn IImIllre iitt ttlhe 'S!DdIiiestt: ({l)if aIIIl1tlbYe ii'SibmInll'S :amrdl giiwe tt:IDWYII!l «\)jf ttlhe~. lTlt iis uiir.dl ttlbmtt: ~ iitt :l!l 1tJruIle Soo1tltil Sea tOIDD.:oxum:. ~ ttIhm: :l!lllle ~ ;mmH lbmti\rrdl iiJm 11498 «lDll rnre «\)jf ~ iislli2ll1lulls \\\VlInDdIn line ~ sallitiiih :are mUlw gIDll)wwu lhmne.. fie ~ ii'S ~ fM "!Ell P'cadrlOO c&e Saonltat M;anU'_ llit ii'S ifino>m ttlInii'S ttlhalt Ulbrese iitt-s ifamooJrs lI:ro!rs:allit IrtOY.ck$., \\WIIniirdIn Ihmw: ~d iitmnlID D:s_.dl$ ~ 1IlIneiiJr ~ mtme_. TIney;:me jjrumt ;a br tOIDlhm!l!lll1l!'£ cammIl .'SlP'lliitt iilm1nol ~ mIDlMliic.. lP~ ~ JlDlRIDjeatitmm; @ mIDdk lriisiilmg \OOlIl1: @fttlhe ~ ttl1niis ii'S ltlhre (QDD]]Y ~ m1Jim:dtii;a ~ ~ mdks m(j)w «(l)j[ AIr_fum Sea IrIOXllllllrdi <allMxmtt: M;m])p.e.. "'Ulme ~ 1IlIJP> m ~ jp)~ if(jj)~. lflIl):(lQ: iisTharrmll ii'S ~ ;a :sqJ_turmre mmiiIke iilm area DWI lIllM mnrOlfIf: ttlhrm_ 15(0) y.anndk; iiIm wMirdhtlIn.. lIlt Jhm; (()1l):Q00JIlIlt ~ D I s T INDIA KARNATAKA DISTRICT UDUPI Km 5 o 5 [0 [5 Km Ul C.D. Block boundary of Udupi is co-terminus o -with laluk boundary , TOTAL AREA OF DISTRICT (IN SQ.KM) __ _______ __ 38.880.00 ..... -. TOTAL POPULATION OF DISTRICT ____________ __ __ 1.112.243 I TOTAL NUMBER OF TOWNS IN" DISTRICT •••• __ ._ .06 :"- TOTAL NU MBER OF VILLAGES [N DISTRICT _____ .