7.Computing Correlation Coefficients
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

04 – Everything You Want to Know About Correlation but Were
EVERYTHING YOU WANT TO KNOW ABOUT CORRELATION BUT WERE AFRAID TO ASK F R E D K U O 1 MOTIVATION • Correlation as a source of confusion • Some of the confusion may arise from the literary use of the word to convey dependence as most people use “correlation” and “dependence” interchangeably • The word “correlation” is ubiquitous in cost/schedule risk analysis and yet there are a lot of misconception about it. • A better understanding of the meaning and derivation of correlation coefficient, and what it truly measures is beneficial for cost/schedule analysts. • Many times “true” correlation is not obtainable, as will be demonstrated in this presentation, what should the risk analyst do? • Is there any other measures of dependence other than correlation? • Concordance and Discordance • Co-monotonicity and Counter-monotonicity • Conditional Correlation etc. 2 CONTENTS • What is Correlation? • Correlation and dependence • Some examples • Defining and Estimating Correlation • How many data points for an accurate calculation? • The use and misuse of correlation • Some example • Correlation and Cost Estimate • How does correlation affect cost estimates? • Portfolio effect? • Correlation and Schedule Risk • How correlation affect schedule risks? • How Shall We Go From Here? • Some ideas for risk analysis 3 POPULARITY AND SHORTCOMINGS OF CORRELATION • Why Correlation Is Popular? • Correlation is a natural measure of dependence for a Multivariate Normal Distribution (MVN) and the so-called elliptical family of distributions • It is easy to calculate analytically; we only need to calculate covariance and variance to get correlation • Correlation and covariance are easy to manipulate under linear operations • Correlation Shortcomings • Variances of R.V. -

11. Correlation and Linear Regression
11. Correlation and linear regression The goal in this chapter is to introduce correlation and linear regression. These are the standard tools that statisticians rely on when analysing the relationship between continuous predictors and continuous outcomes. 11.1 Correlations In this section we’ll talk about how to describe the relationships between variables in the data. To do that, we want to talk mostly about the correlation between variables. But first, we need some data. 11.1.1 The data Table 11.1: Descriptive statistics for the parenthood data. variable min max mean median std. dev IQR Dan’s grumpiness 41 91 63.71 62 10.05 14 Dan’s hours slept 4.84 9.00 6.97 7.03 1.02 1.45 Dan’s son’s hours slept 3.25 12.07 8.05 7.95 2.07 3.21 ............................................................................................ Let’s turn to a topic close to every parent’s heart: sleep. The data set we’ll use is fictitious, but based on real events. Suppose I’m curious to find out how much my infant son’s sleeping habits affect my mood. Let’s say that I can rate my grumpiness very precisely, on a scale from 0 (not at all grumpy) to 100 (grumpy as a very, very grumpy old man or woman). And lets also assume that I’ve been measuring my grumpiness, my sleeping patterns and my son’s sleeping patterns for - 251 - quite some time now. Let’s say, for 100 days. And, being a nerd, I’ve saved the data as a file called parenthood.csv. -

Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10
International Journal of Environmental Research and Public Health Article Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10 Rudy de Barros Ahrens 1,*, Luciana da Silva Lirani 2 and Antonio Carlos de Francisco 3 1 Department of Business, Faculty Sagrada Família (FASF), Ponta Grossa, PR 84010-760, Brazil 2 Department of Health Sciences Center, State University Northern of Paraná (UENP), Jacarezinho, PR 86400-000, Brazil; [email protected] 3 Department of Industrial Engineering and Post-Graduation in Production Engineering, Federal University of Technology—Paraná (UTFPR), Ponta Grossa, PR 84017-220, Brazil; [email protected] * Correspondence: [email protected] Received: 1 September 2020; Accepted: 29 September 2020; Published: 9 October 2020 Abstract: The purpose of this study was to validate the construct and reliability of an instrument to assess the work environment as a single tool based on quality of life (QL), quality of work life (QWL), and organizational climate (OC). The methodology tested the construct validity through Exploratory Factor Analysis (EFA) and reliability through Cronbach’s alpha. The EFA returned a Kaiser–Meyer–Olkin (KMO) value of 0.917; which demonstrated that the data were adequate for the factor analysis; and a significant Bartlett’s test of sphericity (χ2 = 7465.349; Df = 1225; p 0.000). ≤ After the EFA; the varimax rotation method was employed for a factor through commonality analysis; reducing the 14 initial factors to 10. Only question 30 presented commonality lower than 0.5; and the other questions returned values higher than 0.5 in the commonality analysis. Regarding the reliability of the instrument; all of the questions presented reliability as the values varied between 0.953 and 0.956. -
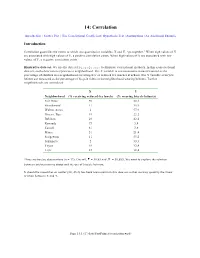
14: Correlation
14: Correlation Introduction | Scatter Plot | The Correlational Coefficient | Hypothesis Test | Assumptions | An Additional Example Introduction Correlation quantifies the extent to which two quantitative variables, X and Y, “go together.” When high values of X are associated with high values of Y, a positive correlation exists. When high values of X are associated with low values of Y, a negative correlation exists. Illustrative data set. We use the data set bicycle.sav to illustrate correlational methods. In this cross-sectional data set, each observation represents a neighborhood. The X variable is socioeconomic status measured as the percentage of children in a neighborhood receiving free or reduced-fee lunches at school. The Y variable is bicycle helmet use measured as the percentage of bicycle riders in the neighborhood wearing helmets. Twelve neighborhoods are considered: X Y Neighborhood (% receiving reduced-fee lunch) (% wearing bicycle helmets) Fair Oaks 50 22.1 Strandwood 11 35.9 Walnut Acres 2 57.9 Discov. Bay 19 22.2 Belshaw 26 42.4 Kennedy 73 5.8 Cassell 81 3.6 Miner 51 21.4 Sedgewick 11 55.2 Sakamoto 2 33.3 Toyon 19 32.4 Lietz 25 38.4 Three are twelve observations (n = 12). Overall, = 30.83 and = 30.883. We want to explore the relation between socioeconomic status and the use of bicycle helmets. It should be noted that an outlier (84, 46.6) has been removed from this data set so that we may quantify the linear relation between X and Y. Page 14.1 (C:\data\StatPrimer\correlation.wpd) Scatter Plot The first step is create a scatter plot of the data. -

Uses for Census Data in Market Research
Uses for Census Data in Market Research MRS Presentation 4 July 2011 Andrew Zelin, Director, Sampling & RMC, Ipsos MORI Why Census Data is so critical to us Use of Census Data underlies almost all of our quantitative work activities and projects Needed to ensure that: – Samples are balanced and representative – ie Sampling; – Results derived from samples reflect that of target population – ie Weighting; – Understanding how demographic and geographic factors affect the findings from surveys – ie Analysis. How would we do our jobs without the use of Census Data? Our work withoutCensusData Our work Regional Assembly What I will cover Introduction, overview and why Census Data is so critical; Census data for sampling; Census data for survey weighting; Census data for statistical analysis; Use of SARs; The future (eg use of “hypercubes”); Our work without Census Data / use of alternatives; Conclusions Census Data for Sampling For Random (pre-selected) Samples: – Need to define stratum sample sizes and sampling fractions; – Need to define cluster size, esp. if PPS – (Need to define stratum / cluster) membership; For any type of Sample: – To balance samples across demographics that cannot be included as quota controls or stratification variables – To determine number of sample points by geography – To create accurate booster samples (eg young people / ethnic groups) Census Data for Sampling For Quota (non-probability) Samples: – To set appropriate quotas (based on demographics); Data are used here at very localised level – ie Census Outputs Census Data for Sampling Census Data for Survey Weighting To ensure that the sample profile balances the population profile Census Data are needed to tell you what the population profile is ….and hence provide accurate weights ….and hence provide an accurate measure of the design effect and the true level of statistical reliability / confidence intervals on your survey measures But also pre-weighting, for interviewer field dept. -

CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (Moderately Hard)Or
5 COMPUTING CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (moderately hard)or WHAT YOU WILLpost, LEARN IN THIS CHAPTER • Understanding what correlations are and how they work • Computing a simple correlation coefficient • Interpretingcopy, the value of the correlation coefficient • Understanding what other types of correlations exist and when they notshould be used Do WHAT ARE CORRELATIONS ALL ABOUT? Measures of central tendency and measures of variability are not the only descrip- tive statistics that we are interested in using to get a picture of what a set of scores 76 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 5 ■ Computing Correlation Coefficients 77 looks like. You have already learned that knowing the values of the one most repre- sentative score (central tendency) and a measure of spread or dispersion (variability) is critical for describing the characteristics of a distribution. However, sometimes we are as interested in the relationship between variables—or, to be more precise, how the value of one variable changes when the value of another variable changes. The way we express this interest is through the computation of a simple correlation coefficient. For example, what’s the relationship between age and strength? Income and years of education? Memory skills and amount of drug use? Your political attitudes and the attitudes of your parents? A correlation coefficient is a numerical index that reflects the relationship or asso- ciation between two variables. The value of this descriptive statistic ranges between −1.00 and +1.00. -

What Is Statistic?
What is Statistic? OPRE 6301 In today’s world. ...we are constantly being bombarded with statistics and statistical information. For example: Customer Surveys Medical News Demographics Political Polls Economic Predictions Marketing Information Sales Forecasts Stock Market Projections Consumer Price Index Sports Statistics How can we make sense out of all this data? How do we differentiate valid from flawed claims? 1 What is Statistics?! “Statistics is a way to get information from data.” Statistics Data Information Data: Facts, especially Information: Knowledge numerical facts, collected communicated concerning together for reference or some particular fact. information. Statistics is a tool for creating an understanding from a set of numbers. Humorous Definitions: The Science of drawing a precise line between an unwar- ranted assumption and a forgone conclusion. The Science of stating precisely what you don’t know. 2 An Example: Stats Anxiety. A business school student is anxious about their statistics course, since they’ve heard the course is difficult. The professor provides last term’s final exam marks to the student. What can be discerned from this list of numbers? Statistics Data Information List of last term’s marks. New information about the statistics class. 95 89 70 E.g. Class average, 65 Proportion of class receiving A’s 78 Most frequent mark, 57 Marks distribution, etc. : 3 Key Statistical Concepts. Population — a population is the group of all items of interest to a statistics practitioner. — frequently very large; sometimes infinite. E.g. All 5 million Florida voters (per Example 12.5). Sample — A sample is a set of data drawn from the population. -

Questionnaire Analysis Using SPSS
Questionnaire design and analysing the data using SPSS page 1 Questionnaire design. For each decision you make when designing a questionnaire there is likely to be a list of points for and against just as there is for deciding on a questionnaire as the data gathering vehicle in the first place. Before designing the questionnaire the initial driver for its design has to be the research question, what are you trying to find out. After that is established you can address the issues of how best to do it. An early decision will be to choose the method that your survey will be administered by, i.e. how it will you inflict it on your subjects. There are typically two underlying methods for conducting your survey; self-administered and interviewer administered. A self-administered survey is more adaptable in some respects, it can be written e.g. a paper questionnaire or sent by mail, email, or conducted electronically on the internet. Surveys administered by an interviewer can be done in person or over the phone, with the interviewer recording results on paper or directly onto a PC. Deciding on which is the best for you will depend upon your question and the target population. For example, if questions are personal then self-administered surveys can be a good choice. Self-administered surveys reduce the chance of bias sneaking in via the interviewer but at the expense of having the interviewer available to explain the questions. The hints and tips below about questionnaire design draw heavily on two excellent resources. SPSS Survey Tips, SPSS Inc (2008) and Guide to the Design of Questionnaires, The University of Leeds (1996). -

4. Introduction to Statistics Descriptive Statistics
Statistics for Engineers 4-1 4. Introduction to Statistics Descriptive Statistics Types of data A variate or random variable is a quantity or attribute whose value may vary from one unit of investigation to another. For example, the units might be headache sufferers and the variate might be the time between taking an aspirin and the headache ceasing. An observation or response is the value taken by a variate for some given unit. There are various types of variate. Qualitative or nominal; described by a word or phrase (e.g. blood group, colour). Quantitative; described by a number (e.g. time till cure, number of calls arriving at a telephone exchange in 5 seconds). Ordinal; this is an "in-between" case. Observations are not numbers but they can be ordered (e.g. much improved, improved, same, worse, much worse). Averages etc. can sensibly be evaluated for quantitative data, but not for the other two. Qualitative data can be analysed by considering the frequencies of different categories. Ordinal data can be analysed like qualitative data, but really requires special techniques called nonparametric methods. Quantitative data can be: Discrete: the variate can only take one of a finite or countable number of values (e.g. a count) Continuous: the variate is a measurement which can take any value in an interval of the real line (e.g. a weight). Displaying data It is nearly always useful to use graphical methods to illustrate your data. We shall describe in this section just a few of the methods available. Discrete data: frequency table and bar chart Suppose that you have collected some discrete data. -

Eight Things You Need to Know About Interpreting Correlations
Research Skills One, Correlation interpretation, Graham Hole v.1.0. Page 1 Eight things you need to know about interpreting correlations: A correlation coefficient is a single number that represents the degree of association between two sets of measurements. It ranges from +1 (perfect positive correlation) through 0 (no correlation at all) to -1 (perfect negative correlation). Correlations are easy to calculate, but their interpretation is fraught with difficulties because the apparent size of the correlation can be affected by so many different things. The following are some of the issues that you need to take into account when interpreting the results of a correlation test. 1. Correlation does not imply causality: This is the single most important thing to remember about correlations. If there is a strong correlation between two variables, it's easy to jump to the conclusion that one of the variables causes the change in the other. However this is not a valid conclusion. If you have two variables, X and Y, it might be that X causes Y; that Y causes X; or that a third factor, Z (or even a whole set of other factors) gives rise to the changes in both X and Y. For example, suppose there is a correlation between how many slices of pizza I eat (variable X), and how happy I am (variable Y). It might be that X causes Y - so that the more pizza slices I eat, the happier I become. But it might equally well be that Y causes X - the happier I am, the more pizza I eat. -

Chapter 11 -- Correlation
Contents 11 Association Between Variables 795 11.4 Correlation . 795 11.4.1 Introduction . 795 11.4.2 Correlation Coe±cient . 796 11.4.3 Pearson's r . 800 11.4.4 Test of Signi¯cance for r . 810 11.4.5 Correlation and Causation . 813 11.4.6 Spearman's rho . 819 11.4.7 Size of r for Various Types of Data . 828 794 Chapter 11 Association Between Variables 11.4 Correlation 11.4.1 Introduction The measures of association examined so far in this chapter are useful for describing the nature of association between two variables which are mea- sured at no more than the nominal scale of measurement. All of these measures, Á, C, Cramer's xV and ¸, can also be used to describe association between variables that are measured at the ordinal, interval or ratio level of measurement. But where variables are measured at these higher levels, it is preferable to employ measures of association which use the information contained in these higher levels of measurement. These higher level scales either rank values of the variable, or permit the researcher to measure the distance between values of the variable. The association between rankings of two variables, or the association of distances between values of the variable provides a more detailed idea of the nature of association between variables than do the measures examined so far in this chapter. While there are many measures of association for variables which are measured at the ordinal or higher level of measurement, correlation is the most commonly used approach. -

Three Kinds of Statistical Literacy: What Should We Teach?
ICOTS6, 2002: Schield THREE KINDS OF STATISTICAL LITERACY: WHAT SHOULD WE TEACH? Milo Schield Augsburg College Minneapolis USA Statistical literacy is analyzed from three different approaches: chance-based, fallacy-based and correlation-based. The three perspectives are evaluated in relation to the needs of employees, consumers, and citizens. A list of the top 35 statistically based trade books in the US is developed and used as a standard for what materials statistically literate people should be able to understand. The utility of each perspective is evaluated by reference to the best sellers within each category. Recommendations are made for what content should be included in pre-college and college statistical literacy textbooks from each kind of statistical literacy. STATISTICAL LITERACY Statistical literacy is a new term and both words (statistical and literacy) are ambiguous. In today’s society literacy means functional literacy: the ability to review, interpret, analyze and evaluate written materials (and to detect errors and flaws therein). Anyone who lacks this type of literacy is functionally illiterate as a productive worker, an informed consumer or a responsible citizen. Functional illiteracy is a modern extension of literal literacy: the ability to read and comprehend written materials. Statistics have two functions depending on whether the data is obtained from a random sample. If a statistic is not from a random sample then one can only do descriptive statistics and statistical modeling even if the data is the entire population. If a statistic is from a random sample then one can also do inferential statistics: sampling distributions, confidence intervals and hypothesis tests.