RESEARCH ARTICLE Identification of Peaks and Summits in Surface Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Complete 230 Fellranger Tick List A
THE LAKE DISTRICT FELLS – PAGE 1 A-F CICERONE Fell name Height Volume Date completed Fell name Height Volume Date completed Allen Crags 784m/2572ft Borrowdale Brock Crags 561m/1841ft Mardale and the Far East Angletarn Pikes 567m/1860ft Mardale and the Far East Broom Fell 511m/1676ft Keswick and the North Ard Crags 581m/1906ft Buttermere Buckbarrow (Corney Fell) 549m/1801ft Coniston Armboth Fell 479m/1572ft Borrowdale Buckbarrow (Wast Water) 430m/1411ft Wasdale Arnison Crag 434m/1424ft Patterdale Calf Crag 537m/1762ft Langdale Arthur’s Pike 533m/1749ft Mardale and the Far East Carl Side 746m/2448ft Keswick and the North Bakestall 673m/2208ft Keswick and the North Carrock Fell 662m/2172ft Keswick and the North Bannerdale Crags 683m/2241ft Keswick and the North Castle Crag 290m/951ft Borrowdale Barf 468m/1535ft Keswick and the North Catbells 451m/1480ft Borrowdale Barrow 456m/1496ft Buttermere Catstycam 890m/2920ft Patterdale Base Brown 646m/2119ft Borrowdale Caudale Moor 764m/2507ft Mardale and the Far East Beda Fell 509m/1670ft Mardale and the Far East Causey Pike 637m/2090ft Buttermere Bell Crags 558m/1831ft Borrowdale Caw 529m/1736ft Coniston Binsey 447m/1467ft Keswick and the North Caw Fell 697m/2287ft Wasdale Birkhouse Moor 718m/2356ft Patterdale Clough Head 726m/2386ft Patterdale Birks 622m/2241ft Patterdale Cold Pike 701m/2300ft Langdale Black Combe 600m/1969ft Coniston Coniston Old Man 803m/2635ft Coniston Black Fell 323m/1060ft Coniston Crag Fell 523m/1716ft Wasdale Blake Fell 573m/1880ft Buttermere Crag Hill 839m/2753ft Buttermere -

Landform Studies in Mosedale, Northeastern Lake District: Opportunities for Field Investigations
Field Studies, 10, (2002) 177 - 206 LANDFORM STUDIES IN MOSEDALE, NORTHEASTERN LAKE DISTRICT: OPPORTUNITIES FOR FIELD INVESTIGATIONS RICHARD CLARK Parcey House, Hartsop, Penrith, Cumbria CA11 0NZ AND PETER WILSON School of Environmental Studies, University of Ulster at Coleraine, Cromore Road, Coleraine, Co. Londonderry BT52 1SA, Northern Ireland (e-mail: [email protected]) ABSTRACT Mosedale is part of the valley of the River Caldew in the Skiddaw upland of the northeastern Lake District. It possesses a diverse, interesting and problematic assemblage of landforms and is convenient to Blencathra Field Centre. The landforms result from glacial, periglacial, fluvial and hillslopes processes and, although some of them have been described previously, others have not. Landforms of one time and environment occur adjacent to those of another. The area is a valuable locality for the field teaching and evaluation of upland geomorphology. In this paper, something of the variety of landforms, materials and processes is outlined for each district in turn. That is followed by suggestions for further enquiry about landform development in time and place. Some questions are posed. These should not be thought of as being the only relevant ones that might be asked about the area: they are intended to help set enquiry off. Mosedale offers a challenge to students at all levels and its landforms demonstrate a complexity that is rarely presented in the textbooks. INTRODUCTION Upland areas attract research and teaching in both earth and life sciences. In part, that is for the pleasure in being there and, substantially, for relative freedom of access to such features as landforms, outcrops and habitats, especially in comparison with intensively occupied lowland areas. -

LOW BECKSIDE FARM Mungrisdale, Cumbria
LOW BECKSIDE FARM mungrisdale, cumbria LOW BECKSIDE FARM MUNGRISDALE, CUMBRIA, CA11 0XR highly regarded upland farm within the lake district national park Traditional farmhouse with four bedrooms Bungalow with three bedrooms Traditional stone barns Extensive modern livestock buildings Lot 1 – Low Beckside Farm set in approx. 195 acres of pasture, plus grazing rights on the common Lot 2 – 209 acres of off lying rough grazing, pasture and woodland IN ALL ABOUT 404 ACRES (163 HECTARES) For sale as a whole or in two lots A66 Trunk Road – 1.6 miles u Keswick – 9 miles u Penrith – 12 miles (All distances are approximate) Savills York Savills Carlisle River House, 17 Museum Street, York, YO1 7DJ 64 Warwick Road, [email protected] Carlisle, CA1 1DR 01904 617831 savills.co.uk Introduction Low Beckside Farm lies to the north of the A66 plantations adds to the amenity aspect of the holding. Across Mungrisdale fell and Bowscale fell. The farm has been in approximately 12 miles west of Penrith and just south of the road is a further 123 acres of permanent pasture plus valuable ELS and HLS Environmental Stewardship Schemes the hamlet of Mungrisdale. The farm has benefited from some rough grazing and woodland. one of which is rolling over on an annual basis. considerable investment in the state of the art livestock building completed in 2017 which was specifically designed Lot 2 comprises approximately 209 acres of pasture and Low Beckside Farm is likely to appeal to commercial farmers for sheep husbandry. The farm in all extends to approximately rough grazing including 29 acres of established woodland as well as lifestyle buyers seeking a manageable sized 404 acres offered for sale in two lots. -

The Western Fells (646M, 2119Ft) the WESTERN FELLS
Seatoller FR OM Blakeley Raise THE BASE BROWN NORTH Heckbarley FR Honister GREY KNOTTS OM GREEN GABLE GRIKE GREAT GABLE Pass THE LANK RIGG BRANDRETH FLEETWITH PIKE SOUTH CRAG FELL FR OM BUCKBARROW HAYSTACKS THE KIRK FELL EAS IRON CRAG Black Sail Pass Whin Fell MIDDLE FELL FR T Stockdale Scarth Gap Mosser OM HIGH CRAG Hatteringill Head Buttermer THE Moor FELLBARROW W SEATALLAN (801m, 2628ft) (801m, asdale WES YEWBARROW HIGH STILE Smithy Fell CAW FELL e Head PILLAR 12 Green Gable Green 12 T Sourfoot Fell BUCKBARROW LOW FELL RED PIKE (W) Darling Dodd GREA SCOAT FELL F Loweswater G ell ABLE GREEN GABLE HAYCOCK STEEPLE Styhead Crummock T RED PIKE (W) Pass SEATALLAN SCOAT FELL MELLBREAK Oswen Fell MIDDLE FELL Black Crag Wa HAYCOCK BRANDRETH te BR BASE (899m, 2949ft) (899m, r STARLING DODD Burnbank Fell OW PILLAR SCOAT FELL W N LOW FELL Lamplugh ast RED PIKE (W) 11 Great Gable Great 11 Sharp Knott Wa Black Crag CAW FELL GREY KNOTTS te FELLBARR BLAKE FELL r HEN COMB PILLAR KNOCK MURTON Honister GREAT BORNE Fothergill Head Pass HIGH CRAG YEWBARROW OW FLEETWITH PIKE GAVEL FELL Carling Knott MELLBREAK HIGH STILE Looking Stead RED PIKE (B) BLAKE FELL (616m, 2021ft) (616m, Burnbank Fell Floutern Cop STARLING DODD Floutern Pass W asdale KIRK FELL Oswen Fell 10 Great Borne Great 10 GREAT BORNE GREAT BORNE Buttermer Head Ennerdale Gale Fell KNOCK MURTON STARLING DODD Floutern Cop e Beck Head Wa RED PIKE (B) te HEN COMB r HIGH STILE GAVEL FELL GREAT GABLE CRAG FELL HIGH CRAG MELLBREAK Scarth Gap GRIKE Crummock THE (526m, 1726ft) (526m, HAYSTACKS Styhead -

4-Night Southern Lake District Guided Walking Holiday
4-Night Southern Lake District Guided Walking Holiday Tour Style: Guided Walking Destinations: Lake District & England Trip code: CNBOB-4 2, 3 & 5 HOLIDAY OVERVIEW Relax and admire magnificent mountain views from our Country House on the shores of Conistonwater. Walk in the footsteps of Wordsworth, Ruskin and Beatrix Potter, as you discover the places that stirred their imaginations. Enjoy the stunning mountain scenes with lakeside strolls, taking a cruise across the lake on the steam yacht Gondola, or enjoy getting nose-to-nose with the high peaks as you explore their heights. Whatever your passion, you’ll be struck with awe as you explore this much-loved area of the Lake District. HOLIDAYS HIGHLIGHTS • Head out on guided walks to discover the varied beauty of the South Lakes on foot • Choose a valley bottom stroll or reach for the summits on fell walks and horseshoe hikes • Let our experienced leaders bring classic routes and hidden gems to life • Visit charming Lakeland villages • A relaxed pace of discovery in a sociable group keen to get some fresh air in one of England’s most beautiful walking areas www.hfholidays.co.uk PAGE 1 [email protected] Tel: +44(0) 20 3974 8865 • Evenings in our country house where you can share a drink and re-live the day’s adventures TRIP SUITABILITY This trip is graded Activity Level 2, 3 and 5. Our best-selling Guided Walking holidays run throughout the year - with their daily choice of up to 3 walks, these breaks are ideal for anyone who enjoys exploring the countryside on foot. -

Hill Bagging 2018
HILL BAGGING 2019 Life before lockdown. Members write about their hill-bagging year: List completions; Simms completion; Core Europe Ultras completion; island bagging; kayaking; climbing; backpacking; close shaves; poems; book reviews; adventures at home and overseas. To jump to an item, click on its title (avoid MS edge browser). Press Ctrl+Home at any time to return to Contents Contents Completions ................................................................................................................................................................... 3 Relative Hills Society Events ........................................................................................................................................... 4 Spring Bagger Rambles, Islay, Port Charlotte YHA: rescheduled to April 23 – 26, 2021 ................................................. 4 Dinner and AGM, The Moorings Hotel, Banavie, Fort William: rescheduled to Sat May 15, 2021 ................................. 4 Summer Isles SIB bagging, Ullapool: hopefully rescheduled to May 2021 .................................................................... 4 Sept 11 – 15, 2020: St Kilda Island Marilyns, Leverburgh, Harris .................................................................................. 4 October – December, 2020: St Kilda Stacs .................................................................................................................. 4 November, 2020 – Autumn Bagger Rambles @TBD ?Northern England ..................................................................... -
2011 'Alerts' Are Now Included Among the List of Incidents - for General Interest and As a Result of a Change in National Reporting Policy
2011 'Alerts' are now included among the list of incidents - for general interest and as a result of a change in national reporting policy. These 'alerts', however, are not added to the tally of 'rescues'. A man, walking alone, reported himself to be lost in the Cat Bells area. We spoke to him on his Cat Bells - Maiden Moor mobile phone and were able to ascertain that he had a torch and GPS and was on a path. Putting 01-Jan 18:59 area everything together, he was advised to walk downhill to, hopefully, arrive in Grange village - which he did by 20:15 hrs. A 46 year old lady slipped on ice and broke her arm. Conditions were very cold, so it was fortunate for all concerned that the Great North Air Ambulance was able to fly to the scene and 1 03-Jan 13:00 Blencathra summit take her to hospital in Carlisle. 15 members - 1 hour 30 minutes 2 walkers got lost in a whiteout and went to ground in a stone shelter. We worked out where they probably were from information given over the phone. We found them very cold but 2 07-Jan 15:20 Bowscale Fell summit otherwise well and walked them back down to the valley. 23 members - 3 hours 25 minutes 2 climbers got into trouble when completing the climb and requested help in getting out of the Great End - Left Hand 3 08-Jan 17:10 gully. They were encountered by 2 other climbers doing the same route, who were able to help Groove them out of their predicament. -

Carrock Fell, June-September 2009 – Part II Mapping Project
Carrock Fell, June-September 2009 – Part II mapping project Last summer I went to the English Lake District and mapped Carrock Fell, a 660-metre hill, and some of the surrounding fell-sides. I was based at a very nice campsite* (in a caravan) just off the main road half way between Penrith and Keswick, and the mapping area was half-an-hour bike ride to the north. The area is visited Conveniently I could cycle along tracks and bridleways quite far into the mapping area in several different places so there wasn’t also a long walk at the start of each day to find somewhere new or interesting to look at! View to E along River Caldew. Carrock Fell on left of photo, Bowscale fell on the right. * Which I would highly recommend to anyone visiting the area – excellent showers, friendly staff, a 30 minute bus ride from Penrith and Keswick, with most of the ‘Northern Fells’ according to Wainwright within walking (if not cycling) distance. For caravans, static caravans and tents†. http://www.campingandcaravanningclub.co.uk/siteseeker/aspx/details.aspx?id=9010 † Incidentally, I’m not on a commission. Unfortunately I did not take a camera with me during mapping, as I would have ended up spending all of my time taking wildlife photos instead of mapping, but as part of the area was visited on the Part IB field trip to Sedbergh, the photos included in this report are from then. I was mainly lucky with the weather, with only a couple of days’ rain; I missed the really bad stuff in August as I was away in Tanzania (as it turns out, four weeks climbing Lakeland fells actually is good training for something like Kilimanjaro). -

PANORAMA from Grisedale Pike (GR 199226)
PANORAMA from Grisedale Pike (GR 199226) PANORAMA Lord’s Seat Seat How Longlands Fell arm f Binsey Skiddaw Blencathra Ling Fell Broom Fell Overwater Ullock Pike Skiddaw Little Man Great Mell Fell Bothelwind North Pennines 3 AONB 2 7 8 4 5 6 1 Comb Dodd Plantation Latrigg KESWICK Hobcarton End PORTINSCALE 1 Whinlatter 2 Ladies Table 3 Brae Fell BRAITHWAITE 4 Long Side 5 Carl Side 6 Carsleddam Kinn N 7 Bowscale Fell 8 Lonscale Fell E Clough Head Raise Great Rigg High Raise Glaramara Great End Great Dodd Helvellyn Ullscarf Pike o’Stickle Bowfell Scafell Pike Fairfield Causey Pike Eagle Crag Dale Head Esk Pike Great Robinson Crag 1 2 3 4 5 11 12 13 6 7 10 14 Walla Crag Maiden Moor High Spy Hindscarth Derwent Water 8 Scar Crags Barrow 9 Sail Stile End Outerside E 1 Stybarrow Dodd 2 White Side 3 Catstycam 4 Nethermost Pike 5 Dollwaggon Pike 6 Bleaberry Fell 7 High Seat S 8 Catbells 9 Rowling End 10 Grange Fell 11 Harrison Stickle 12 Wetherlam 13 Swirl How 14 Great Gable Kirk Fell Eel Crag Red Pike Grasmoor Sand Hill (Buttermere) Gavel Fell Whiteside Hopegill Head Dove Eel Crags Crag Coledale Hause subsidiary top Hobcarton Crag S Hobcarton Gill valley W ISLE OF WHITHORN DUNDRENNEN Bengairn Screel Hill KIPPFORD DUMFRIES Whinlatter Low F ell F ellbarrow Covend Coast Criffel Caerlaverock Hatteringill Head Solway Firth COCKERMOUTH Graystones Ling Fell Swinside Hobcarton End W Hobcarton Gill valley N This graphic is an extract from The North-Western Fells, volume six in the Lakeland Fellranger series to be published in April 2011 by Cicerone Press Ltd (c) Mark Richards 2010. -

Complete the Wainwright's in 36 Walks - the Check List Thirty-Six Circular Walks Covering All the Peaks in Alfred Wainwright's Pictorial Guides to the Lakeland Fells
Complete the Wainwright's in 36 Walks - The Check List Thirty-six circular walks covering all the peaks in Alfred Wainwright's Pictorial Guides to the Lakeland Fells. This list is provided for those of you wishing to complete the Wainwright's in 36 walks. Simply tick off each mountain as completed when the task of climbing it has been accomplished. Mountain Book Walk Completed Arnison Crag The Eastern Fells Greater Grisedale Horseshoe Birkhouse Moor The Eastern Fells Greater Grisedale Horseshoe Birks The Eastern Fells Greater Grisedale Horseshoe Catstye Cam The Eastern Fells A Glenridding Circuit Clough Head The Eastern Fells St John's Vale Skyline Dollywaggon Pike The Eastern Fells Greater Grisedale Horseshoe Dove Crag The Eastern Fells Greater Fairfield Horseshoe Fairfield The Eastern Fells Greater Fairfield Horseshoe Glenridding Dodd The Eastern Fells A Glenridding Circuit Gowbarrow Fell The Eastern Fells Mell Fell Medley Great Dodd The Eastern Fells St John's Vale Skyline Great Mell Fell The Eastern Fells Mell Fell Medley Great Rigg The Eastern Fells Greater Fairfield Horseshoe Hart Crag The Eastern Fells Greater Fairfield Horseshoe Hart Side The Eastern Fells A Glenridding Circuit Hartsop Above How The Eastern Fells Kirkstone and Dovedale Circuit Helvellyn The Eastern Fells Greater Grisedale Horseshoe Heron Pike The Eastern Fells Greater Fairfield Horseshoe Mountain Book Walk Completed High Hartsop Dodd The Eastern Fells Kirkstone and Dovedale Circuit High Pike (Scandale) The Eastern Fells Greater Fairfield Horseshoe Little Hart Crag -

The Northern Fells
Northern Lake District Wainwright Bagging Holiday - the Northern Fells Tour Style: Guided Walking Destinations: Lake District & England Trip code: DBWBC Trip Walking Grade: 6 HOLIDAY OVERVIEW Wainwright bagging, perfect when you want to release your inner explorer! Alfred Wainwright’s Pictorial Guides have provided the inspiration for many a fell walker, with over two million copies of the books selling since their publication. There are 214 fells described within his books and this holiday takes in all of the fells he enthuses about in his Northern Fells pictorial guide, in one fabulous, challenging holiday. Bag the Northern Fell Wainwrights of the Lake District with fellow walking enthusiasts as you experience a moorland feel in a quiet, remote area north of the other ranges. Each day, our experienced leaders will be taking you to 4 to 6 Wainwrights covering over 10 miles of ground – discovering magnificent views to Scotland, walking the well known Skiddaw mountain and visiting local, upbeat market towns. WHAT'S INCLUDED • Great value: all prices include Full Board en-suite accommodation, a full programme of walks with all transport to and from the walks, and evening activities • Great walking: enjoy the challenge of bagging all of the summits in Wainwright’s Northern Fells pictorial www.hfholidays.co.uk PAGE 1 [email protected] Tel: +44(0) 20 3974 8865 guide, accompanied by an experienced leader • Accommodation: enjoy a lakeside location just two miles from Keswick, with fantastic views of the surrounding fells HOLIDAYS HIGHLIGHTS -
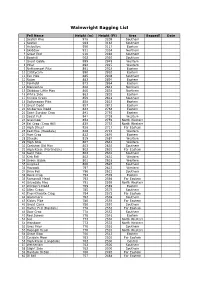
Wainwright Bagging List
Wainwright Bagging List Fell Name Height (m) Height (Ft) Area Bagged? Date 1 Scafell Pike 978 3209 Southern 2 Scafell 964 3163 Southern 3 Helvellyn 950 3117 Eastern 4 Skiddaw 931 3054 Northern 5 Great End 910 2986 Southern 6 Bowfell 902 2959 Southern 7 Great Gable 899 2949 Western 8 Pillar 892 2927 Western 9 Nethermost Pike 891 2923 Eastern 10 Catstycam 890 2920 Eastern 11 Esk Pike 885 2904 Southern 12 Raise 883 2897 Eastern 13 Fairfield 873 2864 Eastern 14 Blencathra 868 2848 Northern 15 Skiddaw Little Man 865 2838 Northern 16 White Side 863 2832 Eastern 17 Crinkle Crags 859 2818 Southern 18 Dollywagon Pike 858 2815 Eastern 19 Great Dodd 857 2812 Eastern 20 Stybarrow Dodd 843 2766 Eastern 21 Saint Sunday Crag 841 2759 Eastern 22 Scoat Fell 841 2759 Western 23 Grasmoor 852 2759 North Western 24 Eel Crag (Crag Hill) 839 2753 North Western 25 High Street 828 2717 Far Eastern 26 Red Pike (Wasdale) 826 2710 Western 27 Hart Crag 822 2697 Eastern 28 Steeple 819 2687 Western 29 High Stile 807 2648 Western 30 Coniston Old Man 803 2635 Southern 31 High Raise (Martindale) 802 2631 Far Eastern 32 Swirl How 802 2631 Southern 33 Kirk Fell 802 2631 Western 34 Green Gable 801 2628 Western 35 Lingmell 800 2625 Southern 36 Haycock 797 2615 Western 37 Brim Fell 796 2612 Southern 38 Dove Crag 792 2598 Eastern 39 Rampsgill Head 792 2598 Far Eastern 40 Grisedale Pike 791 2595 North Western 41 Watson's Dodd 789 2589 Eastern 42 Allen Crags 785 2575 Southern 43 Thornthwaite Crag 784 2572 Far Eastern 44 Glaramara 783 2569 Southern 45 Kidsty Pike 780 2559 Far