DOCSLIB.ORG

Analysis of Variance: the Fundamental Concepts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Analysis of Variance: the Fundamental Concepts Analysis of Variance: The Fundamental Concepts STEVEN F. SAWYER, PT, PhD nalysis of variance (ANOVA) is a procedures (or post hoc tests), effect size, ANOVA General Linear Models statistical tool used to detect differ- statistical power, etc. How do these terms ences between experimental group pertain to p values and statistical signifi- ANOVA is based mathematically on lin- A ear regression and general linear models means. ANOVA is warranted in experi- cance? What precisely is meant by a “sta- mental designs with one dependent vari- tistically significant ANOVA”? How does that quantify the relationship between the dependent variable and the indepen- able that is a continuous parametric nu- analyzing variance result in an inferential 1 merical outcome measure, and multiple decision about differences in group dent variable(s) . There are three different experimental groups within one or more means? Can ANOVA be performed on general linear models for ANOVA: (i) independent (categorical) variables. In non-parametric data? What are the vir- Fixed effects model (Model 1)makes infer- ANOVA terminology, independent vari- tues and potential pitfalls of ANOVA? ences that are specific and valid only to ables are called factors, and groups within These are the issues to be addressed in the populations and treatments of the each factor are referred to as levels. The this primer on the use and interpretation study. For example, if three treatments array of terms that are part and parcel of of ANOVA. The intent is to provide the involve three different doses of a drug, ANOVA can be intimidating to the un- clinician reader, whose misspent youth inferential conclusions can only be drawn initiated, such as: partitioning of vari- did not include an enthusiastic reading of for those specific drug doses. The levels ance, main effects, interactions, factors, statistics textbooks, an understanding of within each factor are fixed as defined by sum of squares, mean squares, F scores, the fundamentals of this widely used the experimental design. (ii) Random ef- familywise alpha, multiple comparison form of inferential statistical analysis. fects model (Model 2) makes inferences about levels of the factor that are not used in the study, such as a continuum of drug doses when the study only used three ABSTRACT: Analysis of variance (ANOVA) is a statistical test for detecting differences doses. This model pertains to random ef- in group means when there is one parametric dependent variable and one or more indepen- fects within levels, and makes inferences dent variables. This article summarizes the fundamentals of ANOVA for an intended benefit about a population’s random variation. of the clinician reader of scientific literature who does not possess expertise in statistics. The (iii) Mixed effects model (Model 3) con- emphasis is on conceptually-based perspectives regarding the use and interpretation of tains both Fixed and Random effects. ANOVA, with minimal coverage of the mathematical foundations. Computational exam- In most types of orthopedic reha- ples are provided. Assumptions underlying ANOVA include parametric data measures, bilitation clinical research, the Fixed ef- normally distributed data, similar group variances, and independence of subjects. However, fects model is relevant since the statistical normality and variance assumptions can often be violated with impunity if sample sizes are inferences being sought are fixed to the sufficiently large and there are equal numbers of subjects in each group. A statistically sig- levels of the experimental design. For this nificant ANOVA is typically followed up with a multiple comparison procedure to identify reason, the Fixed effects model will be the which group means differ from each other. The article concludes with a discussion of effect focus of this article. Computer statistics size and the important distinction between statistical significance and clinical significance. programs typically default to the Fixed KEYWORDS: Analysis of Variance, Interaction, Main Effects, Multiple Comparison effects model for ANOVA analysis, but Procedures higher end programs can perform ANOVA with all three models. Department of Rehabilitation Sciences, School of Allied Health Sciences, Texas Tech University Health Sciences Center, Lubbock, TX Address all correspondence and requests for reprints to: Steven F. Sawyer, PT, PhD, [email protected] THE JOURNAL OF MANUAL & MANIPULATIVE THERAPY n VOLUME 17 n NUMBER 2 [E27] ANALYSIS OF VARIANCE: THE FUNDAMENtaL CONCEPTS Assumptions of ANOVA as a way to infer whether the normal dis- A normal distribution curve will have tribution curves of different data sets are skewness = 0 and kurtosis = 3. (Note that Assumptions for ANOVA pertain to the best thought of as being from the same an alternative definition of kurtosis sub- underlying mathematics of general lin- population or different populations tracts 3 from the final value so that a ear models. Specifically, a data set should (Figure 1). It follows that a fundamental normal distribution will have kurtosis = meet the following criteria before being assumption of parametric ANOVA is 0. This “minus 3” kurtosis value is some- subjected to ANOVA: that each group of data (each level) be times referred to as “excess kurtosis” to Parametric data: A parametric normally distributed. The Shapiro-Wilk distinguish it from the value obtained ANOVA, the topic of this article, re- test2 is commonly used to test for nor- with the standard kurtosis function. The quires parametric data (ratio or interval mality for group sample sizes (N) less kurtosis value calculated by many statis- measures). There are non-parametric, than 50; D’Agnostino’s modification3 is tical programs is the “minus 3” variant one-factor versions of ANOVA for non- useful for larger samplings (N>50). but is referred to, somewhat mislead- parametric ordinal (ranked) data, spe- A normal distribution curve can be ingly, as “kurtosis.”). Normality of a data cifically the Kruskal-Wallis test for inde- described by whether it has symmetry set can be assessed with a z-test in refer- pendent groups and the Friedman test about the mean and the appropriate ence to the standard error of skewness for repeated measures analysis. width and height (peakedness). These (estimated as √[6 / N) and the standard Normally distributed data within attributes are defined statistically by error of kurtosis (estimated as √[24 / each group: ANOVA can be thought of “skewness” and “kurtosis”, respectively. N)4. A conservative alpha of 0.01 (z ≥ FIGURE 1. Graphical representation of statistical Null and Alternative hypotheses for ANOVA in the case of one dependent variable (change in ankle ROM pre/post manual therapy treatment, in units of degrees), and one independent variable with three levels (three different types of manual therapy treatments). For this fictitious data, the group (sample) means are 13, 14 and 18 degrees of increased ankle ROM for treatment type groups 1, 2 and 3, respectively (raw data are presented in Figure 2). The Null hypothesis is represented in the left graph, in which the population means for all three groups are assumed be identical to each other (in spite of difference in sample means calculated from the experimental data). Since in the Null hypothesis the subjects in the three groups are considered to compose a single population, by definition the population means of each group are equal to each other, and are equal to the Grand mean (mean for all data scores in the three groups). The corresponding normal distribution curves are identical and precisely overlap along the X-axis. The Alternative hypothesis is shown in right graph, in which differences in group sample means are inferred to represent true differences in group population means. These normal distribution curves do not overlap along the X-axis because each group of subjects are considered to be distinct populations with respect to ankle ROM, created from the original single population that experienced different efficacies of the three treatments. Graph is patterned after Wilkinson et al11. ANOVA Null Hypothesis: ANOVA Null Hypothesis: Identical Normal distribution curve Different Normal distribution curve ensity Function ensity Function D D robability robability robability P P Increased elbow ROM (degree) Increased elbow ROM (degree) [E28] THE JOURNAL OF MANUAL & MANIPULATIVE THERAPY n VOLUME 17 n NUMBER 2 ANALYSIS OF VARIANCE: THE FUNDAMENtaL CONCEPTS 2.56) is appropriate, due to the overly the F score calculation are warranted. so9,10. If normality and homogeneity of sensitive nature of these tests, especially The two most commonly used correc- variance violations are problematic, for large sample sizes (>100)4. As a com- tion methods are the Greenhouse- there are three options: (i) Mathemati- putational example, for N = 20, the esti- Geisser and Huynh-Feldt, which calcu- cally transform (log, arcsin, etc.) the mation of standard error of skewness = late a descriptive statistic called epsilon, data to best mitigate the violation, with √[6 / 20] = 0.55, and any skewness value which is a measure of the extent to which the cost of cognitive fog in understand- greater than ±2.56 x 0.55 = ±1.41 would sphericity has been violated. The range ing the meaning to the ANOVA results indicate non-normality. Perhaps the of values for epsilon are 1 (no sphericity (e.g., “A statistically significant main ef- best “test” is what always should be violation) to a lower boundary of 1 / fect was obtained for the arcsin transfor- done: examine a histogram of the distri- (m—1), where m = number of levels. For mation of degrees of ankle range of mo- bution of the data. In practice, any dis- example, with three groups, the range tion”). (ii) Use one of the non-parametric tribution that resembles a bell-shaped would be 1 to 0.50. The closer epsilon is ANOVAs mentioned above, but at the curve will be “normal enough” to pass to the lower boundary, the greater the cost of reduced power and being limited normality tests, especially if the sample degree of violation.
Load more

Recommended publications
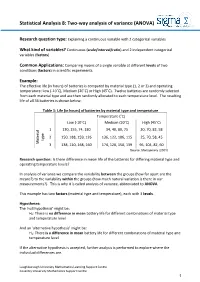
  • Statistical Analysis 8: Two-Way Analysis of Variance (ANOVA)
    Statistical Analysis 8: Two-way analysis of variance (ANOVA) Research question type: Explaining a continuous variable with 2 categorical variables What kind of variables? Continuous (scale/interval/ratio) and 2 independent categorical variables (factors) Common Applications: Comparing means of a single variable at different levels of two conditions (factors) in scientific experiments. Example: The effective life (in hours) of batteries is compared by material type (1, 2 or 3) and operating temperature: Low (-10˚C), Medium (20˚C) or High (45˚C). Twelve batteries are randomly selected from each material type and are then randomly allocated to each temperature level. The resulting life of all 36 batteries is shown below: Table 1: Life (in hours) of batteries by material type and temperature Temperature (˚C) Low (-10˚C) Medium (20˚C) High (45˚C) 1 130, 155, 74, 180 34, 40, 80, 75 20, 70, 82, 58 2 150, 188, 159, 126 136, 122, 106, 115 25, 70, 58, 45 type Material 3 138, 110, 168, 160 174, 120, 150, 139 96, 104, 82, 60 Source: Montgomery (2001) Research question: Is there difference in mean life of the batteries for differing material type and operating temperature levels? In analysis of variance we compare the variability between the groups (how far apart are the means?) to the variability within the groups (how much natural variation is there in our measurements?). This is why it is called analysis of variance, abbreviated to ANOVA. This example has two factors (material type and temperature), each with 3 levels. Hypotheses: The 'null hypothesis' might be: H0: There is no difference in mean battery life for different combinations of material type and temperature level And an 'alternative hypothesis' might be: H1: There is a difference in mean battery life for different combinations of material type and temperature level If the alternative hypothesis is accepted, further analysis is performed to explore where the individual differences are.
    [Show full text]
  • 5. Dummy-Variable Regression and Analysis of Variance
    Sociology 740 John Fox Lecture Notes 5. Dummy-Variable Regression and Analysis of Variance Copyright © 2014 by John Fox Dummy-Variable Regression and Analysis of Variance 1 1. Introduction I One of the limitations of multiple-regression analysis is that it accommo- dates only quantitative explanatory variables. I Dummy-variable regressors can be used to incorporate qualitative explanatory variables into a linear model, substantially expanding the range of application of regression analysis. c 2014 by John Fox Sociology 740 ° Dummy-Variable Regression and Analysis of Variance 2 2. Goals: I To show how dummy regessors can be used to represent the categories of a qualitative explanatory variable in a regression model. I To introduce the concept of interaction between explanatory variables, and to show how interactions can be incorporated into a regression model by forming interaction regressors. I To introduce the principle of marginality, which serves as a guide to constructing and testing terms in complex linear models. I To show how incremental I -testsareemployedtotesttermsindummy regression models. I To show how analysis-of-variance models can be handled using dummy variables. c 2014 by John Fox Sociology 740 ° Dummy-Variable Regression and Analysis of Variance 3 3. A Dichotomous Explanatory Variable I The simplest case: one dichotomous and one quantitative explanatory variable. I Assumptions: Relationships are additive — the partial effect of each explanatory • variable is the same regardless of the specific value at which the other explanatory variable is held constant. The other assumptions of the regression model hold. • I The motivation for including a qualitative explanatory variable is the same as for including an additional quantitative explanatory variable: to account more fully for the response variable, by making the errors • smaller; and to avoid a biased assessment of the impact of an explanatory variable, • as a consequence of omitting another explanatory variables that is relatedtoit.
    [Show full text]
  • Analysis of Variance and Analysis of Variance and Design of Experiments of Experiments-I
    Analysis of Variance and Design of Experimentseriments--II MODULE ––IVIV LECTURE - 19 EXPERIMENTAL DESIGNS AND THEIR ANALYSIS Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur 2 Design of experiment means how to design an experiment in the sense that how the observations or measurements should be obtained to answer a qqyuery inavalid, efficient and economical way. The desigggning of experiment and the analysis of obtained data are inseparable. If the experiment is designed properly keeping in mind the question, then the data generated is valid and proper analysis of data provides the valid statistical inferences. If the experiment is not well designed, the validity of the statistical inferences is questionable and may be invalid. It is important to understand first the basic terminologies used in the experimental design. Experimental unit For conducting an experiment, the experimental material is divided into smaller parts and each part is referred to as experimental unit. The experimental unit is randomly assigned to a treatment. The phrase “randomly assigned” is very important in this definition. Experiment A way of getting an answer to a question which the experimenter wants to know. Treatment Different objects or procedures which are to be compared in an experiment are called treatments. Sampling unit The object that is measured in an experiment is called the sampling unit. This may be different from the experimental unit. 3 Factor A factor is a variable defining a categorization. A factor can be fixed or random in nature. • A factor is termed as fixed factor if all the levels of interest are included in the experiment.
    [Show full text]
  • Statistical Significance Testing in Information Retrieval:An Empirical
    Statistical Significance Testing in Information Retrieval: An Empirical Analysis of Type I, Type II and Type III Errors Julián Urbano Harlley Lima Alan Hanjalic Delft University of Technology Delft University of Technology Delft University of Technology The Netherlands The Netherlands The Netherlands [email protected] [email protected] [email protected] ABSTRACT 1 INTRODUCTION Statistical significance testing is widely accepted as a means to In the traditional test collection based evaluation of Information assess how well a difference in effectiveness reflects an actual differ- Retrieval (IR) systems, statistical significance tests are the most ence between systems, as opposed to random noise because of the popular tool to assess how much noise there is in a set of evaluation selection of topics. According to recent surveys on SIGIR, CIKM, results. Random noise in our experiments comes from sampling ECIR and TOIS papers, the t-test is the most popular choice among various sources like document sets [18, 24, 30] or assessors [1, 2, 41], IR researchers. However, previous work has suggested computer but mainly because of topics [6, 28, 36, 38, 43]. Given two systems intensive tests like the bootstrap or the permutation test, based evaluated on the same collection, the question that naturally arises mainly on theoretical arguments. On empirical grounds, others is “how well does the observed difference reflect the real difference have suggested non-parametric alternatives such as the Wilcoxon between the systems and not just noise due to sampling of topics”? test. Indeed, the question of which tests we should use has accom- Our field can only advance if the published retrieval methods truly panied IR and related fields for decades now.
    [Show full text]
  • THE ONE-SAMPLE Z TEST
    10 THE ONE-SAMPLE z TEST Only the Lonely Difficulty Scale ☺ ☺ ☺ (not too hard—this is the first chapter of this kind, but youdistribute know more than enough to master it) or WHAT YOU WILL LEARN IN THIS CHAPTERpost, • Deciding when the z test for one sample is appropriate to use • Computing the observed z value • Interpreting the z value • Understandingcopy, what the z value means • Understanding what effect size is and how to interpret it not INTRODUCTION TO THE Do ONE-SAMPLE z TEST Lack of sleep can cause all kinds of problems, from grouchiness to fatigue and, in rare cases, even death. So, you can imagine health care professionals’ interest in seeing that their patients get enough sleep. This is especially the case for patients 186 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 10 ■ The One-Sample z Test 187 who are ill and have a real need for the healing and rejuvenating qualities that sleep brings. Dr. Joseph Cappelleri and his colleagues looked at the sleep difficul- ties of patients with a particular illness, fibromyalgia, to evaluate the usefulness of the Medical Outcomes Study (MOS) Sleep Scale as a measure of sleep problems. Although other analyses were completed, including one that compared a treat- ment group and a control group with one another, the important analysis (for our discussion) was the comparison of participants’ MOS scores with national MOS norms. Such a comparison between a sample’s mean score (the MOS score for par- ticipants in this study) and a population’s mean score (the norms) necessitates the use of a one-sample z test.
    [Show full text]
  • Tests of Hypotheses Using Statistics
    Tests of Hypotheses Using Statistics Adam Massey¤and Steven J. Millery Mathematics Department Brown University Providence, RI 02912 Abstract We present the various methods of hypothesis testing that one typically encounters in a mathematical statistics course. The focus will be on conditions for using each test, the hypothesis tested by each test, and the appropriate (and inappropriate) ways of using each test. We conclude by summarizing the di®erent tests (what conditions must be met to use them, what the test statistic is, and what the critical region is). Contents 1 Types of Hypotheses and Test Statistics 2 1.1 Introduction . 2 1.2 Types of Hypotheses . 3 1.3 Types of Statistics . 3 2 z-Tests and t-Tests 5 2.1 Testing Means I: Large Sample Size or Known Variance . 5 2.2 Testing Means II: Small Sample Size and Unknown Variance . 9 3 Testing the Variance 12 4 Testing Proportions 13 4.1 Testing Proportions I: One Proportion . 13 4.2 Testing Proportions II: K Proportions . 15 4.3 Testing r £ c Contingency Tables . 17 4.4 Incomplete r £ c Contingency Tables Tables . 18 5 Normal Regression Analysis 19 6 Non-parametric Tests 21 6.1 Tests of Signs . 21 6.2 Tests of Ranked Signs . 22 6.3 Tests Based on Runs . 23 ¤E-mail: [email protected] yE-mail: [email protected] 1 7 Summary 26 7.1 z-tests . 26 7.2 t-tests . 27 7.3 Tests comparing means . 27 7.4 Variance Test . 28 7.5 Proportions . 28 7.6 Contingency Tables .
    [Show full text]
  • Statistical Significance
    Statistical significance In statistical hypothesis testing,[1][2] statistical signif- 1.1 Related concepts icance (or a statistically significant result) is at- tained whenever the observed p-value of a test statis- The significance level α is the threshhold for p below tic is less than the significance level defined for the which the experimenter assumes the null hypothesis is study.[3][4][5][6][7][8][9] The p-value is the probability of false, and something else is going on. This means α is obtaining results at least as extreme as those observed, also the probability of mistakenly rejecting the null hy- given that the null hypothesis is true. The significance pothesis, if the null hypothesis is true.[22] level, α, is the probability of rejecting the null hypothe- Sometimes researchers talk about the confidence level γ sis, given that it is true.[10] This statistical technique for = (1 − α) instead. This is the probability of not rejecting testing the significance of results was developed in the the null hypothesis given that it is true. [23][24] Confidence early 20th century. levels and confidence intervals were introduced by Ney- In any experiment or observation that involves drawing man in 1937.[25] a sample from a population, there is always the possibil- ity that an observed effect would have occurred due to sampling error alone.[11][12] But if the p-value of an ob- 2 Role in statistical hypothesis test- served effect is less than the significance level, an inves- tigator may conclude that that effect reflects the charac- ing teristics of the
    [Show full text]
  • Understanding Statistical Hypothesis Testing: the Logic of Statistical Inference
    Review Understanding Statistical Hypothesis Testing: The Logic of Statistical Inference Frank Emmert-Streib 1,2,* and Matthias Dehmer 3,4,5 1 Predictive Society and Data Analytics Lab, Faculty of Information Technology and Communication Sciences, Tampere University, 33100 Tampere, Finland 2 Institute of Biosciences and Medical Technology, Tampere University, 33520 Tampere, Finland 3 Institute for Intelligent Production, Faculty for Management, University of Applied Sciences Upper Austria, Steyr Campus, 4040 Steyr, Austria 4 Department of Mechatronics and Biomedical Computer Science, University for Health Sciences, Medical Informatics and Technology (UMIT), 6060 Hall, Tyrol, Austria 5 College of Computer and Control Engineering, Nankai University, Tianjin 300000, China * Correspondence: [email protected]; Tel.: +358-50-301-5353 Received: 27 July 2019; Accepted: 9 August 2019; Published: 12 August 2019 Abstract: Statistical hypothesis testing is among the most misunderstood quantitative analysis methods from data science. Despite its seeming simplicity, it has complex interdependencies between its procedural components. In this paper, we discuss the underlying logic behind statistical hypothesis testing, the formal meaning of its components and their connections. Our presentation is applicable to all statistical hypothesis tests as generic backbone and, hence, useful across all application domains in data science and artificial intelligence. Keywords: hypothesis testing; machine learning; statistics; data science; statistical inference 1. Introduction We are living in an era that is characterized by the availability of big data. In order to emphasize the importance of this, data have been called the ‘oil of the 21st Century’ [1]. However, for dealing with the challenges posed by such data, advanced analysis methods are needed.
    [Show full text]
  • ANALYSIS of VARIANCE and MISSING OBSERVATIONS in COMPLETELY RANDOMIZED, RANDOMIZED BLOCKS and LATIN SQUARE DESIGNS a Thesis
    ANALYSIS OF VARIANCE AND MISSING OBSERVATIONS IN COMPLETELY RANDOMIZED, RANDOMIZED BLOCKS AND LATIN SQUARE DESIGNS A Thesis Presented to The Department of Mathematics Kansas State Teachers College, Emporia, Kansas In Partial Fulfillment of the Requirements for the Degree Master of Science by Kiritkumar K. Talati May 1972 c; , ACKNOWLEDGEMENTS Sincere thanks and gratitude is expressed to Dr. John Burger for his assistance, patience, and his prompt attention in all directions in preparing this paper. A special note of appreciation goes to Dr. Marion Emerson, Dr. Thomas Davis, Dr. George Poole, Dr. Darrell Wood, who rendered assistance in the research of this paper. TABLE OF CONTENTS CHAPTER I. INTRODUCTION • • • • • • • • • • • • • • • • 1 A. Preliminary Consideration. • • • • • • • 1 B. Purpose and Assumptions of the Analysis of Variance • • • • • • • • •• 1 C. Analysis of Covariance • • • • • • • • • 2 D. Definitions. • • • • • • • • • • • • • • ) E. Organization of Paper. • • • • • • • • • 4 II. COMPLETELY RANDOMIZED DESIGN • • • • • • • • 5 A. Description............... 5 B. Randomization. • • • • • • • • • • • • • 5 C. Problem and Computations •••••••• 6 D. Conclusion and Further Applications. •• 10 III. RANDOMIZED BLOCK DESIGN. • • • • • • • • • • 12 A. Description............... 12 B. Randomization. • • • • • • • • • • • • • 1) C. Problem and Statistical Analysis • • • • 1) D. Efficiency of Randomized Block Design as Compared to Completely Randomized Design. • • • • • • • • • •• 20 E. Missing Observations • • • • • • • • •• 21 F.
    [Show full text]
  • What Are Confidence Intervals and P-Values?
    What is...? series Second edition Statistics Supported by sanofi-aventis What are confidence intervals and p-values? G A confidence interval calculated for a measure of treatment effect Huw TO Davies PhD shows the range within which the true treatment effect is likely to lie Professor of Health (subject to a number of assumptions). Care Policy and G A p-value is calculated to assess whether trial results are likely to have Management, occurred simply through chance (assuming that there is no real University of St difference between new treatment and old, and assuming, of course, Andrews that the study was well conducted). Iain K Crombie PhD G Confidence intervals are preferable to p-values, as they tell us the range FFPHM Professor of of possible effect sizes compatible with the data. Public Health, G p-values simply provide a cut-off beyond which we assert that the University of Dundee findings are ‘statistically significant’ (by convention, this is p<0.05). G A confidence interval that embraces the value of no difference between treatments indicates that the treatment under investigation is not significantly different from the control. G Confidence intervals aid interpretation of clinical trial data by putting upper and lower bounds on the likely size of any true effect. G Bias must be assessed before confidence intervals can be interpreted. Even very large samples and very narrow confidence intervals can mislead if they come from biased studies. G Non-significance does not mean ‘no effect’. Small studies will often report non-significance even when there are important, real effects which a large study would have detected.
    [Show full text]
  • Understanding Statistical Significance: a Short Guide
    UNDERSTANDING STATISTICAL SIGNIFICANCE: A SHORT GUIDE Farooq Sabri and Tracey Gyateng September 2015 Using a control or comparison group is a powerful way to measure the impact of an intervention, but doing this in a robust way requires statistical expertise. NPC’s Data Labs project, funded by the Oak Foundation, aims to help charities by opening up government data that will allow organisations to compare the longer-term outcomes of their service to non-users. This guide explains the terminology used in comparison group analysis and how to interpret the results. Introduction With budgets tightening across the charity sector, it is helpful to test whether services are actually helping beneficiaries by measuring their impact. Robust evaluation means assessing whether programmes have made a difference over and above what would have happened without them1. This is known as the ‘counterfactual’. Obviously we can only estimate this difference. The best way to do so is to find a control or comparison group2 of people who have similar characteristics to the service users, the only difference being that they did not receive the intervention in question. Assessment is made by comparing the outcomes for service users with the comparison group to see if there is any statistically significant difference. Creating comparison groups and testing for statistical significance can involve complex calculations, and interpreting the results can be difficult, especially when the result is not clear cut. That’s why NPC launched the Data Labs project to respond to this need for robust quantitative evaluations. This paper is designed as an introduction to the field, explaining the key terminology to non-specialists.
    [Show full text]
  • Analysis of Variance in the Modern Design of Experiments
    Analysis of Variance in the Modern Design of Experiments Richard DeLoach* NASA Langley Research Center, Hampton, Virginia, 23681 This paper is a tutorial introduction to the analysis of variance (ANOVA), intended as a reference for aerospace researchers who are being introduced to the analytical methods of the Modern Design of Experiments (MDOE), or who may have other opportunities to apply this method. One-way and two-way fixed-effects ANOVA, as well as random effects ANOVA, are illustrated in practical terms that will be familiar to most practicing aerospace researchers. I. Introduction he Modern Design of Experiments (MDOE) is an integrated system of experiment design, execution, and T analysis procedures based on industrial experiment design methods introduced at the beginning of the 20th century for various product and process improvement applications. MDOE is focused on the complexities and special requirements of aerospace ground testing. It was introduced to the experimental aeronautics community at NASA Langley Research Center in the 1990s as part of a renewed focus on quality and productivity improvement in wind tunnel testing, and has been used since then in numerous other applications as well. MDOE has been offered as a more productive, less costly, and higher quality alternative to conventional testing methods used widely in the aerospace industry, and known in the literature of experiment design as ―One Factor At a Time‖ (OFAT) testing. The basic principles of MDOE are documented in the references1-4, and some representative examples of its application in aerospace research are also provided5-16. The MDOE method provides productivity advantages over conventional testing methods by generating more information per data point.
    [Show full text]