Exploratory Factor Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Anomalous Perception in a Ganzfeld Condition - a Meta-Analysis of More Than 40 Years Investigation [Version 1; Peer Review: Awaiting Peer Review]](https://docslib.b-cdn.net/cover/5459/anomalous-perception-in-a-ganzfeld-condition-a-meta-analysis-of-more-than-40-years-investigation-version-1-peer-review-awaiting-peer-review-5459.webp)
Anomalous Perception in a Ganzfeld Condition - a Meta-Analysis of More Than 40 Years Investigation [Version 1; Peer Review: Awaiting Peer Review]
F1000Research 2021, 10:234 Last updated: 08 SEP 2021 RESEARCH ARTICLE Stage 2 Registered Report: Anomalous perception in a Ganzfeld condition - A meta-analysis of more than 40 years investigation [version 1; peer review: awaiting peer review] Patrizio E. Tressoldi 1, Lance Storm2 1Studium Patavinum, University of Padua, Padova, Italy 2School of Psychology, University of Adelaide, Adelaide, Australia v1 First published: 24 Mar 2021, 10:234 Open Peer Review https://doi.org/10.12688/f1000research.51746.1 Latest published: 24 Mar 2021, 10:234 https://doi.org/10.12688/f1000research.51746.1 Reviewer Status AWAITING PEER REVIEW Any reports and responses or comments on the Abstract article can be found at the end of the article. This meta-analysis is an investigation into anomalous perception (i.e., conscious identification of information without any conventional sensorial means). The technique used for eliciting an effect is the ganzfeld condition (a form of sensory homogenization that eliminates distracting peripheral noise). The database consists of studies published between January 1974 and December 2020 inclusive. The overall effect size estimated both with a frequentist and a Bayesian random-effect model, were in close agreement yielding an effect size of .088 (.04-.13). This result passed four publication bias tests and seems not contaminated by questionable research practices. Trend analysis carried out with a cumulative meta-analysis and a meta-regression model with Year of publication as covariate, did not indicate sign of decline of this effect size. The moderators analyses show that selected participants outcomes were almost three-times those obtained by non-selected participants and that tasks that simulate telepathic communication show a two- fold effect size with respect to tasks requiring the participants to guess a target. -

Dentist's Knowledge of Evidence-Based Dentistry and Digital Applications Resources in Saudi Arabia
PTB Reports Research Article Dentist’s Knowledge of Evidence-based Dentistry and Digital Applications Resources in Saudi Arabia Yousef Ahmed Alomi*, BSc. Pharm, MSc. Clin Pharm, BCPS, BCNSP, DiBA, CDE ABSTRACT Critical Care Clinical Pharmacists, TPN Objectives: Drug information resources provide clinicians with safer use of medications and play a Clinical Pharmacist, Freelancer Business vital role in improving drug safety. Evidence-based medicine (EBM) has become essential to medical Planner, Content Editor, and Data Analyst, Riyadh, SAUDI ARABIA. practice; however, EBM is still an emerging dentistry concept. Therefore, in this study, we aimed to Anwar Mouslim Alshammari, B.D.S explore dentists’ knowledge about evidence-based dentistry resources in Saudi Arabia. Methods: College of Destiney, Hail University, SAUDI This is a 4-month cross-sectional study conducted to analyze dentists’ knowledge about evidence- ARABIA. based dentistry resources in Saudi Arabia. We included dentists from interns to consultants and Hanin Sumaydan Saleam Aljohani, those across all dentistry specialties and located in Saudi Arabia. The survey collected demographic Ministry of Health, Riyadh, SAUDI ARABIA. information and knowledge of resources on dental drugs. The knowledge of evidence-based dental care and knowledge of dental drug information applications. The survey was validated through the Correspondence: revision of expert reviewers and pilot testing. Moreover, various reliability tests had been done with Dr. Yousef Ahmed Alomi, BSc. Pharm, the study. The data were collected through the Survey Monkey system and analyzed using Statistical MSc. Clin Pharm, BCPS, BCNSP, DiBA, CDE Critical Care Clinical Pharmacists, TPN Package of Social Sciences (SPSS) and Jeffery’s Amazing Statistics Program (JASP). -

04 – Everything You Want to Know About Correlation but Were
EVERYTHING YOU WANT TO KNOW ABOUT CORRELATION BUT WERE AFRAID TO ASK F R E D K U O 1 MOTIVATION • Correlation as a source of confusion • Some of the confusion may arise from the literary use of the word to convey dependence as most people use “correlation” and “dependence” interchangeably • The word “correlation” is ubiquitous in cost/schedule risk analysis and yet there are a lot of misconception about it. • A better understanding of the meaning and derivation of correlation coefficient, and what it truly measures is beneficial for cost/schedule analysts. • Many times “true” correlation is not obtainable, as will be demonstrated in this presentation, what should the risk analyst do? • Is there any other measures of dependence other than correlation? • Concordance and Discordance • Co-monotonicity and Counter-monotonicity • Conditional Correlation etc. 2 CONTENTS • What is Correlation? • Correlation and dependence • Some examples • Defining and Estimating Correlation • How many data points for an accurate calculation? • The use and misuse of correlation • Some example • Correlation and Cost Estimate • How does correlation affect cost estimates? • Portfolio effect? • Correlation and Schedule Risk • How correlation affect schedule risks? • How Shall We Go From Here? • Some ideas for risk analysis 3 POPULARITY AND SHORTCOMINGS OF CORRELATION • Why Correlation Is Popular? • Correlation is a natural measure of dependence for a Multivariate Normal Distribution (MVN) and the so-called elliptical family of distributions • It is easy to calculate analytically; we only need to calculate covariance and variance to get correlation • Correlation and covariance are easy to manipulate under linear operations • Correlation Shortcomings • Variances of R.V. -

11. Correlation and Linear Regression
11. Correlation and linear regression The goal in this chapter is to introduce correlation and linear regression. These are the standard tools that statisticians rely on when analysing the relationship between continuous predictors and continuous outcomes. 11.1 Correlations In this section we’ll talk about how to describe the relationships between variables in the data. To do that, we want to talk mostly about the correlation between variables. But first, we need some data. 11.1.1 The data Table 11.1: Descriptive statistics for the parenthood data. variable min max mean median std. dev IQR Dan’s grumpiness 41 91 63.71 62 10.05 14 Dan’s hours slept 4.84 9.00 6.97 7.03 1.02 1.45 Dan’s son’s hours slept 3.25 12.07 8.05 7.95 2.07 3.21 ............................................................................................ Let’s turn to a topic close to every parent’s heart: sleep. The data set we’ll use is fictitious, but based on real events. Suppose I’m curious to find out how much my infant son’s sleeping habits affect my mood. Let’s say that I can rate my grumpiness very precisely, on a scale from 0 (not at all grumpy) to 100 (grumpy as a very, very grumpy old man or woman). And lets also assume that I’ve been measuring my grumpiness, my sleeping patterns and my son’s sleeping patterns for - 251 - quite some time now. Let’s say, for 100 days. And, being a nerd, I’ve saved the data as a file called parenthood.csv. -

Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10
International Journal of Environmental Research and Public Health Article Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10 Rudy de Barros Ahrens 1,*, Luciana da Silva Lirani 2 and Antonio Carlos de Francisco 3 1 Department of Business, Faculty Sagrada Família (FASF), Ponta Grossa, PR 84010-760, Brazil 2 Department of Health Sciences Center, State University Northern of Paraná (UENP), Jacarezinho, PR 86400-000, Brazil; [email protected] 3 Department of Industrial Engineering and Post-Graduation in Production Engineering, Federal University of Technology—Paraná (UTFPR), Ponta Grossa, PR 84017-220, Brazil; [email protected] * Correspondence: [email protected] Received: 1 September 2020; Accepted: 29 September 2020; Published: 9 October 2020 Abstract: The purpose of this study was to validate the construct and reliability of an instrument to assess the work environment as a single tool based on quality of life (QL), quality of work life (QWL), and organizational climate (OC). The methodology tested the construct validity through Exploratory Factor Analysis (EFA) and reliability through Cronbach’s alpha. The EFA returned a Kaiser–Meyer–Olkin (KMO) value of 0.917; which demonstrated that the data were adequate for the factor analysis; and a significant Bartlett’s test of sphericity (χ2 = 7465.349; Df = 1225; p 0.000). ≤ After the EFA; the varimax rotation method was employed for a factor through commonality analysis; reducing the 14 initial factors to 10. Only question 30 presented commonality lower than 0.5; and the other questions returned values higher than 0.5 in the commonality analysis. Regarding the reliability of the instrument; all of the questions presented reliability as the values varied between 0.953 and 0.956. -
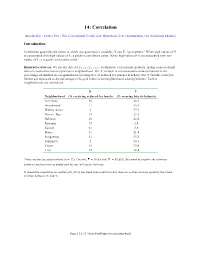
14: Correlation
14: Correlation Introduction | Scatter Plot | The Correlational Coefficient | Hypothesis Test | Assumptions | An Additional Example Introduction Correlation quantifies the extent to which two quantitative variables, X and Y, “go together.” When high values of X are associated with high values of Y, a positive correlation exists. When high values of X are associated with low values of Y, a negative correlation exists. Illustrative data set. We use the data set bicycle.sav to illustrate correlational methods. In this cross-sectional data set, each observation represents a neighborhood. The X variable is socioeconomic status measured as the percentage of children in a neighborhood receiving free or reduced-fee lunches at school. The Y variable is bicycle helmet use measured as the percentage of bicycle riders in the neighborhood wearing helmets. Twelve neighborhoods are considered: X Y Neighborhood (% receiving reduced-fee lunch) (% wearing bicycle helmets) Fair Oaks 50 22.1 Strandwood 11 35.9 Walnut Acres 2 57.9 Discov. Bay 19 22.2 Belshaw 26 42.4 Kennedy 73 5.8 Cassell 81 3.6 Miner 51 21.4 Sedgewick 11 55.2 Sakamoto 2 33.3 Toyon 19 32.4 Lietz 25 38.4 Three are twelve observations (n = 12). Overall, = 30.83 and = 30.883. We want to explore the relation between socioeconomic status and the use of bicycle helmets. It should be noted that an outlier (84, 46.6) has been removed from this data set so that we may quantify the linear relation between X and Y. Page 14.1 (C:\data\StatPrimer\correlation.wpd) Scatter Plot The first step is create a scatter plot of the data. -
![Arxiv:1908.07390V1 [Stat.AP] 19 Aug 2019](https://docslib.b-cdn.net/cover/4781/arxiv-1908-07390v1-stat-ap-19-aug-2019-334781.webp)
Arxiv:1908.07390V1 [Stat.AP] 19 Aug 2019
An Overview of Statistical Data Analysis Rui Portocarrero Sarmento Vera Costa LIAAD-INESC TEC FEUP, University of Porto PRODEI - FEUP, University of Porto [email protected] [email protected] August 21, 2019 Abstract The use of statistical software in academia and enterprises has been evolving over the last years. More often than not, students, professors, workers and users in general have all had, at some point, exposure to statistical software. Sometimes, difficulties are felt when dealing with such type of software. Very few persons have theoretical knowledge to clearly understand software configurations or settings, and sometimes even the presented results. Very often, the users are required by academies or enterprises to present reports, without the time to explore or understand the results or tasks required to do a optimal prepara- tion of data or software settings. In this work, we present a statistical overview of some theoretical concepts, to provide a fast access to some concepts. Keywords Reporting Mathematics Statistics and Applications · · 1 Introduction Statistics is a set of methods used to analyze data. The statistic is present in all areas of science involving the collection, handling and sorting of data, given the insight of a particular phenomenon and the possibility that, from that knowledge, inferring possible new results. One of the goals with statistics is to extract information from data to get a better understanding of the situations they represent. Thus, the statistics can be thought of as the science of learning from data. Currently, the high competitiveness in search technologies and markets has caused a constant race for the information. -

Discriminant Function Analysis
Discriminant Function Analysis Discriminant Function Analysis ● General Purpose ● Computational Approach ● Stepwise Discriminant Analysis ● Interpreting a Two-Group Discriminant Function ● Discriminant Functions for Multiple Groups ● Assumptions ● Classification General Purpose Discriminant function analysis is used to determine which variables discriminate between two or more naturally occurring groups. For example, an educational researcher may want to investigate which variables discriminate between high school graduates who decide (1) to go to college, (2) to attend a trade or professional school, or (3) to seek no further training or education. For that purpose the researcher could collect data on numerous variables prior to students' graduation. After graduation, most students will naturally fall into one of the three categories. Discriminant Analysis could then be used to determine which variable(s) are the best predictors of students' subsequent educational choice. A medical researcher may record different variables relating to patients' backgrounds in order to learn which variables best predict whether a patient is likely to recover completely (group 1), partially (group 2), or not at all (group 3). A biologist could record different characteristics of similar types (groups) of flowers, and then perform a discriminant function analysis to determine the set of characteristics that allows for the best discrimination between the types. To index Computational Approach Computationally, discriminant function analysis is very similar to analysis of variance (ANOVA ). Let us consider a simple example. Suppose we measure height in a random sample of 50 males and 50 females. Females are, on the average, not as tall as http://www.statsoft.com/textbook/stdiscan.html (1 of 11) [2/11/2008 8:56:30 AM] Discriminant Function Analysis males, and this difference will be reflected in the difference in means (for the variable Height ). -

Factor Analysis
Factor Analysis Qian-Li Xue Biostatistics Program Harvard Catalyst | The Harvard Clinical & Translational Science Center Short course, October 27, 2016 1 Well-used latent variable models Latent Observed variable scale variable scale Continuous Discrete Continuous Factor Discrete FA analysis IRT (item response) LISREL Discrete Latent profile Latent class Growth mixture analysis, regression General software: MPlus, Latent Gold, WinBugs (Bayesian), NLMIXED (SAS) Objectives § What is factor analysis? § What do we need factor analysis for? § What are the modeling assumptions? § How to specify, fit, and interpret factor models? § What is the difference between exploratory and confirmatory factor analysis? § What is and how to assess model identifiability? 3 What is factor analysis § Factor analysis is a theory driven statistical data reduction technique used to explain covariance among observed random variables in terms of fewer unobserved random variables named factors 4 An Example: General Intelligence (Charles Spearman, 1904) Y1 δ1 δ Y2 2 δ General Y3 3 Intelligence Y4 δ4 F Y5 δ5 5 Why Factor Analysis? 1. Testing of theory § Explain covariation among multiple observed variables by § Mapping variables to latent constructs (called “factors”) 2. Understanding the structure underlying a set of measures § Gain insight to dimensions § Construct validation (e.g., convergent validity) 3. Scale development § Exploit redundancy to improve scale’s validity and reliability 6 Part I. Exploratory Factor Analysis (EFA) 7 One Common Factor Model: Model Specification Y δ1 λ1 1 Y1 = λ1F +δ1 λ2 Y δ F 2 2 Y2 = λ2 F +δ 2 λ3 Y δ 3 3 Y3 = λ3F +δ3 § The factor F is not observed; only Y1, Y2, Y3 are observed § δi represent variability in the Yi NOT explained by F § Yi is a linear function of F and δi 8 One Common Factor Model: Model Assumptions λ Y δ1 1 1 Y1 = λ1F +δ1 λ2 Y δ F 2 2 Y2 = λ2 F +δ 2 λ3 Y δ 3 3 Y3 = λ3F +δ3 § Factorial causation § F is independent of δj, i.e. -

CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (Moderately Hard)Or
5 COMPUTING CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (moderately hard)or WHAT YOU WILLpost, LEARN IN THIS CHAPTER • Understanding what correlations are and how they work • Computing a simple correlation coefficient • Interpretingcopy, the value of the correlation coefficient • Understanding what other types of correlations exist and when they notshould be used Do WHAT ARE CORRELATIONS ALL ABOUT? Measures of central tendency and measures of variability are not the only descrip- tive statistics that we are interested in using to get a picture of what a set of scores 76 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 5 ■ Computing Correlation Coefficients 77 looks like. You have already learned that knowing the values of the one most repre- sentative score (central tendency) and a measure of spread or dispersion (variability) is critical for describing the characteristics of a distribution. However, sometimes we are as interested in the relationship between variables—or, to be more precise, how the value of one variable changes when the value of another variable changes. The way we express this interest is through the computation of a simple correlation coefficient. For example, what’s the relationship between age and strength? Income and years of education? Memory skills and amount of drug use? Your political attitudes and the attitudes of your parents? A correlation coefficient is a numerical index that reflects the relationship or asso- ciation between two variables. The value of this descriptive statistic ranges between −1.00 and +1.00. -

Covid-19 Epidemiological Factor Analysis: Identifying Principal Factors with Machine Learning
medRxiv preprint doi: https://doi.org/10.1101/2020.06.01.20119560; this version posted June 5, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. It is made available under a CC-BY-NC-ND 4.0 International license . Covid-19 Epidemiological Factor Analysis: Identifying Principal Factors with Machine Learning Serge Dolgikh1[0000-0001-5929-8954] Abstract. Based on a subset of Covid-19 Wave 1 cases at a time point near TZ+3m (April, 2020), we perform an analysis of the influencing factors for the epidemics impacts with several different statistical methods. The consistent con- clusion of the analysis with the available data is that apart from the policy and management quality, being the dominant factor, the most influential factors among the considered were current or recent universal BCG immunization and the prevalence of smoking. Keywords: Infectious epidemiology, Covid-19 1 Introduction A possible link between the effects of Covid-19 pandemics such as the rate of spread and the severity of cases; and a universal immunization program against tuberculosis with BCG vaccine (UIP, hereinafter) was suggested in [1] and further investigated in [2]. Here we provide a factor analysis based on the available data for the first group of countries that encountered the epidemics (Wave 1) by applying several commonly used factor-ranking methods. The intent of the work is to repeat similar analysis at several different points in the time series of cases that would allow to make a confident conclusion about the epide- miological and social factors with strong influence on the course of the epidemics. -

T-Test & Factor Analysis
University of Brighton Parametric tests T-test & factor analysis Better than non parametric tests Stringent assumptions More strings attached Assumes population distribution of sample is normal Major problem Alternatives • Continue using parametric test if the sample is large or enough evidence available to prove the usage • Transforming and manipulating variables • Use non parametric test Dr. Paurav Shukla t-test Tests used for significant differences between Used when they are two groups only groups Compares the mean score on some continuous Independent sample t-test variable Paired sample t-test Largely used in measuring before – after effect One-way ANOVA (between groups) Also called intervention effect One-way ANOVA (repeated groups) Option 1: Same sample over a period of time Two-way ANOVA (between groups) Option 2: Two different groups at a single point of MANOVA time Assumptions associated with t-test Why t-test is important? Population distribution of sample is normal Highly used technique for hypothesis testing Probability (random) sampling Can lead to wrong conclusions Level of measurement Type 1 error Dependent variable is continuous • Reject null hypothesis instead of accepting – When we assume there is a difference between groups, when it Observed or measured data must be is not independent Type 2 error If interaction is unavoidable use a stringent alpha • Accept null hypothesis instead of rejecting value (p<.01) – When we assume there is no difference between groups, when Homogeneity of variance there is Assumes that samples are obtained from populations Solution of equal variance • Interdependency between both errors ANOVA is reasonably robust against this • Selection of alpha level Dr.