Linking Rivers in the Ganges-Brahmaputra River Basin: Exploring the Transboundary Effects
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Interlinking of Rivers in India: Proposed Sharda-Yamuna Link
IOSR Journal of Environmental Science, Toxicology and Food Technology (IOSR-JESTFT) e-ISSN: 2319-2402,p- ISSN: 2319-2399.Volume 9, Issue 2 Ver. II (Feb 2015), PP 28-35 www.iosrjournals.org Interlinking of rivers in India: Proposed Sharda-Yamuna Link Anjali Verma and Narendra Kumar Department of Environmental Science, Babasaheb Bhimrao Ambedkar University (A Central University), Lucknow-226025, (U.P.), India. Abstract: Currently, about a billion people around the world are facing major water problems drought and flood. The rainfall in the country is irregularly distributed in space and time causes drought and flood. An approach for effective management of droughts and floods at the national level; the Central Water Commission formulated National Perspective Plan (NPP) in the year, 1980 and developed a plan called “Interlinking of Rivers in India”. The special feature of the National Perspective Plan is to provide proper distribution of water by transferring water from surplus basin to deficit basin. About 30 interlinking of rivers are proposed on 37 Indian rivers under NPP plan. Sharda to Yamuna Link is one of the proposed river inter links. The main concern of the paper is to study the proposed inter-basin water transfer Sharda – Yamuna Link including its size, area and location of the project. The enrouted and command areas of the link canal covers in the States of Uttarakhand and Uttar Pradesh in India. The purpose of S-Y link canal is to transfer the water from surplus Sharda River to deficit Yamuna River for use of water in drought prone western areas like Uttar Pradesh, Haryana, Rajasthan and Gujarat of the country. -

The Conservation Action Plan the Ganges River Dolphin
THE CONSERVATION ACTION PLAN FOR THE GANGES RIVER DOLPHIN 2010-2020 National Ganga River Basin Authority Ministry of Environment & Forests Government of India Prepared by R. K. Sinha, S. Behera and B. C. Choudhary 2 MINISTER’S FOREWORD I am pleased to introduce the Conservation Action Plan for the Ganges river dolphin (Platanista gangetica gangetica) in the Ganga river basin. The Gangetic Dolphin is one of the last three surviving river dolphin species and we have declared it India's National Aquatic Animal. Its conservation is crucial to the welfare of the Ganga river ecosystem. Just as the Tiger represents the health of the forest and the Snow Leopard represents the health of the mountainous regions, the presence of the Dolphin in a river system signals its good health and biodiversity. This Plan has several important features that will ensure the existence of healthy populations of the Gangetic dolphin in the Ganga river system. First, this action plan proposes a set of detailed surveys to assess the population of the dolphin and the threats it faces. Second, immediate actions for dolphin conservation, such as the creation of protected areas and the restoration of degraded ecosystems, are detailed. Third, community involvement and the mitigation of human-dolphin conflict are proposed as methods that will ensure the long-term survival of the dolphin in the rivers of India. This Action Plan will aid in their conservation and reduce the threats that the Ganges river dolphin faces today. Finally, I would like to thank Dr. R. K. Sinha , Dr. S. K. Behera and Dr. -

Assessment on the Impact of the Tripura Earthquake
www.gi.sanu.ac.rs, www.doiserbia.nb.rs J. Geogr. Inst. Cvijic. 2021, 71(1), pp. 1–13 Original scientific paper UDC: 911.2:5580.34(540)“2017” https://doi.org/10.2298/IJGI2101001D Received: October 8, 2020 Reviewed: March 15, 2021 Accepted: March 22, 2021 ASSESSMENT ON THE IMPACT OF THE TRIPURA EARTHQUAKE (JANUARY 3, 2017, MW = 5.6) IN NORTHEAST INDIA Jimmi Debbarma1, Jatan Debnath1* 1Tripura University, Department of Geography & Disaster Management, Suryamaninagar, Tripura, India; e-mails: [email protected]; [email protected] Abstract: The northeastern part of the Indian subcontinent, considered as the most active seismic zone of the Indian subcontinent, was hit by an earthquake of Mw 5.6 on January 3, 2017. The epicenter of this earthquake was Kanchanbari located in the Dhalai district of Tripura. The present study aims to assess the environmental and socio-economic impact of this earthquake in the vicinity of the epicenter. To assess and determine the level of damage, the affected areas were visited during the first week of the 2017 earthquake. Various Government offices were also consulted to acquire data on damages caused by the earthquake. Moreover, Remote Sensing and Geographical Information System (RS & GIS) techniques were applied to address the influence of this earthquake on bank erosion. During the field visit, the striking features of soil liquefaction generated by the earthquake were observed in the flood plain area of the Manu River. Landslide, with three casualties in India and the neighbor Bangladesh, and damages of infrastructure were also reported. Additionally, an assessment of the bank erosion study revealed that the rate of the post-earthquake bank erosion increased to 592%, compared to the pre-earthquake bank erosion within the study length of the Manu River. -

National Ganga River Basin Authority (Ngrba)
NATIONAL GANGA RIVER BASIN AUTHORITY (NGRBA) Public Disclosure Authorized (Ministry of Environment and Forests, Government of India) Public Disclosure Authorized Environmental and Social Management Framework (ESMF) Public Disclosure Authorized Volume I - Environmental and Social Analysis March 2011 Prepared by Public Disclosure Authorized The Energy and Resources Institute New Delhi i Table of Contents Executive Summary List of Tables ............................................................................................................... iv Chapter 1 National Ganga River Basin Project ....................................................... 6 1.1 Introduction .................................................................................................. 6 1.2 Ganga Clean up Initiatives ........................................................................... 6 1.3 The Ganga River Basin Project.................................................................... 7 1.4 Project Components ..................................................................................... 8 1.4.1.1 Objective ...................................................................................................... 8 1.4.1.2 Sub Component A: NGRBA Operationalization & Program Management 9 1.4.1.3 Sub component B: Technical Assistance for ULB Service Provider .......... 9 1.4.1.4 Sub-component C: Technical Assistance for Environmental Regulator ... 10 1.4.2.1 Objective ................................................................................................... -

Water Wars: the Brahmaputra River and Sino-Indian Relations
U.S. Naval War College U.S. Naval War College Digital Commons CIWAG Case Studies 10-2013 Water Wars: The Brahmaputra River and Sino-Indian Relations Mark Christopher Follow this and additional works at: https://digital-commons.usnwc.edu/ciwag-case-studies Recommended Citation Christopher, Mark, "MIWS_07 - Water Wars: The Brahmaputra River and Sino-Indian Relations" (2013). CIWAG Case Studies. 7. https://digital-commons.usnwc.edu/ciwag-case-studies/7 This Book is brought to you for free and open access by U.S. Naval War College Digital Commons. It has been accepted for inclusion in CIWAG Case Studies by an authorized administrator of U.S. Naval War College Digital Commons. For more information, please contact [email protected]. Draft as of 121916 ARF R W ARE LA a U nd G A E R R M R I E D n o G R R E O T U N P E S C U N E IT EG ED L S OL TA R C TES NAVAL WA Water Wars: The Brahmaputra River and Sino-Indian Relations Mark Christopher United States Naval War College Newport, Rhode Island Water Wars: The Brahmaputra River and Sino-Indian Relations Mark Christopher Center on Irregular Warfare & Armed Groups (CIWAG) US Naval War College, Newport, RI [email protected] CHRISTOPHER: WATER WARS CIWAG Case Studies Bureaucracy Does Its Thing (in Afghanistan) – Todd Greentree Operationalizing Intelligence Dominance – Roy Godson An Operator’s Guide to Human Terrain Teams – Norman Nigh Organizational Learning and the Marine Corps: The Counterinsurgency Campaign in Iraq – Richard Shultz Piracy – Martin Murphy Reading the Tea Leaves: Proto-Insurgency in Honduras – John D. -

Protection of Endangered Ganges River Dolphin in Brahmaputra River, Assam, India
PROTECTION OF ENDANGERED GANGES RIVER DOLPHIN IN BRAHMAPUTRA RIVER, ASSAM, INDIA Final Technical Report to Sir Peter Scott Fund, IUCN Report submitted by - Abdul Wakid, Ph. D. Programme Leader Gangetic Dolphin Research & Conservation Programme, Aaranyak Survey, Beltola, Guwahati-781028 Assam, India Gill Braulik Sea Mammal Research Unit University of St. Andrews St. Andrews, Fife KY16 8LB, UK Page | 2 ACKNOWLEDGEMENT We are expressing our sincere thanks to Sir Peter Scott Fund of IUCN for funding this project. We are thankful to the Department of Environment & Forest (wildlife) and the management authority of Kaziranga National Park, Government of Assam for the permission to carry out the study, especially within Kaziranga National Park. Without the tremendous help of Sanjay Das, Dhruba Chetry, Abdul Mazid and Lalan Sanjib Baruah, the Project would not have reached its current status and we are therefore grateful to all these team members for their field assistance. The logistic support provided by the DFO of Tinsukia Wildlife Division and the Mongoldoi Wildlife Division are highly acknowledged. Special thanks to Inspector General of Police (special branch) of Assam Police Department for organizing the security of the survey team in all districts in the Brahamputra Valley. In particular Colonel Sanib, Captain Amrit, Captain Bikash of the Indian Army for the security arrangement in Assam-Arunachal Pradesh border and Assistant Commandant Vijay Singh of the Border Security Force for security help in the India-Bangladesh border area. We also express our sincere thanks to the Director of Inland Water Transport, Alfresco River Cruise, Mr. Kono Phukan, Mr. Bhuban Pegu and Mr. -

Water Resource Competition in the Brahmaputra River Basin: China, India, and Bangladesh Nilanthi Samaranayake, Satu Limaye, and Joel Wuthnow
Water Resource Competition in the Brahmaputra River Basin: China, India, and Bangladesh Nilanthi Samaranayake, Satu Limaye, and Joel Wuthnow May 2016 Distribution unlimited This document represents the best opinion of CNA at the time of issue. Distribution Distribution unlimited. Specific authority contracting number: 14-106755-000-INP. For questions or comments about this study, contact Nilanthi Samaranayake at [email protected] Cover Photography: Brahmaputra River, India: people crossing the Brahmaputra River at six in the morning. Credit: Encyclopædia Britannica ImageQuest, "Brahmaputra River, India," Maria Stenzel / National Geographic Society / Universal Images Group Rights Managed / For Education Use Only, http://quest.eb.com/search/137_3139899/1/137_3139899/cite. Approved by: May 2016 Ken E Gause, Director International Affairs Group Center for Strategic Studies Copyright © 2016 CNA Abstract The Brahmaputra River originates in China and runs through India and Bangladesh. China and India have fought a war over contested territory through which the river flows, and Bangladesh faces human security pressures in this basin that will be magnified by upstream river practices. Controversial dam-building activities and water diversion plans could threaten regional stability; yet, no bilateral or multilateral water management accord exists in the Brahmaputra basin. This project, sponsored by the MacArthur Foundation, provides greater understanding of the equities and drivers fueling water insecurity in the Brahmaputra River basin. After conducting research in Dhaka, New Delhi, and Beijing, CNA offers recommendations for key stakeholders to consider at the subnational, bilateral, and multilateral levels to increase cooperation in the basin. These findings lay the foundation for policymakers in China, India, and Bangladesh to discuss steps that help manage and resolve Brahmaputra resource competition, thereby strengthening regional security. -

Conservation of Gangetic Dolphin in Brahmaputra River System, India
CONSERVATION OF GANGETIC DOLPHIN IN BRAHMAPUTRA RIVER SYSTEM, INDIA Final Technical Report A. Wakid Project Leader, Gangetic Dolphin Conservation Project Assam, India Email: [email protected] 2 ACKNOWLEDGEMENT There was no comprehensive data on the conservation status of Gangetic dolphin in Brahmaputra river system for last 12 years. Therefore, it was very important to undertake a detail study on the species from the conservation point of view in the entire river system within Assam, based on which site and factor specific conservation actions would be worthwhile. However, getting the sponsorship to conduct this task in a huge geographical area of about 56,000 sq. km. itself was a great problem. The support from the BP Conservation Programme (BPCP) and the Rufford Small Grant for Nature Conservation (RSG) made it possible for me. I am hereby expressing my sincere thanks to both of these Funding Agencies for their great support to save this endangered species. Besides their enormous workload, Marianne Dunn, Dalgen Robyn, Kate Stoke and Jaimye Bartake of BPCP spent a lot of time for my Project and for me through advise, network and capacity building, which helped me in successful completion of this project. I am very much grateful to all of them. Josh Cole, the Programme Manager of RSG encouraged me through his visit to my field area in April, 2005. I am thankful to him for this encouragement. Simon Mickleburgh and Dr. Martin Fisher (Flora & Fauna International), Rosey Travellan (Tropical Biology Association), Gill Braulik (IUCN), Brian Smith (IUCN), Rundall Reeves (IUCN), Dr. A. R. Rahmani (BNHS), Prof. -
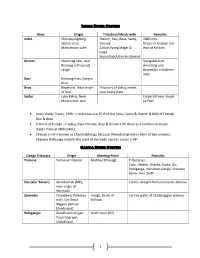
1 Indus River System River Origin Tributries/Meets with Remarks
Indus River System River Origin Tributries/Meets with Remarks Indus Chemayungdung Jhelum, Ravi, Beas, Satluj, 2880 Kms Glacier near Chenab Drains in Arabian sea Mansarovar Lake Zaskar,Syang,Shigar & east of Karachi Gilgit Shyok,Kabul,Kurram,Gomal Jhelum Sheshnag lake, near Navigable b/w Beninag in Pirpanjal Anantnag and range Baramulla in Kashmir vally Ravi Rohtang Pass, Kangra Distt. Beas Beaskund, Near origin Tributary of Satluj, meets of Ravi near Kapurthala Satluj Lake Rakas, Near Enters HP near Shipki Mansarovar lake La Pass Indus Water Treaty, 1960 :-> India can use 20 % of the Indus, Satluj & Jhelum & 80% of Chenab Ravi & Beas 5 Rivers of Punjab :-> Satluj, Ravi, Chenab, Beas & Jhelum ( All these as a combined stream meets Indus at Mithankot) Chenab in HP is known as Chandrabhanga because Chenab originate in form of two streams: Chandra & Bhanga on both the sides of the Bada Laccha La pass in HP. Ganga River System Ganga Tributary Origin Meeting Point Remarks Yamuna Yamunotri Glaciar Allahbad (Prayag) Tributaries: Tons, Hindon, Sharda, Kunta, Gir, Rishiganga, Hanuman Ganga, Chambal, Betwa, Ken, Sindh Son (aka ‘Savan’) Amarkantak (MP), Comes straight from peninsular plateau near origin of Narmada Damodar Chandawa, Palamau Hoogli, South of Carries water of Chotanagpur plateau distt. On Chota Kolkata Nagpur plateau (Jharkhand) Ramganga: Doodhatoli ranges, Ibrahimpur (UP) Pauri Gharwal, Uttrakhand 1 Gandak Nhubine Himal Glacier, Sonepur, Bihar It originates as ‘Kali Gandak’ Tibet-Mustang border Called ‘Narayani’ in Nepal nepal Bhuri Gandak Bisambharpur, West Khagaria, Bihar Champaran district Bhagmati Where three headwater streams converge at Bāghdwār above the southern edge of the Shivapuri Hills about 15 km northeast of Kathmandu Kosi near Kursela in the Formed by three main streams: the Katihar district Tamur Koshi originating from Mt. -

Reconciling Drainage and Receiving Basin Signatures of the Godavari River System
Biogeosciences, 15, 3357–3375, 2018 https://doi.org/10.5194/bg-15-3357-2018 © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Reconciling drainage and receiving basin signatures of the Godavari River system Muhammed Ojoshogu Usman1, Frédérique Marie Sophie Anne Kirkels2, Huub Michel Zwart2, Sayak Basu3, Camilo Ponton4, Thomas Michael Blattmann1, Michael Ploetze5, Negar Haghipour1,6, Cameron McIntyre1,6,7, Francien Peterse2, Maarten Lupker1, Liviu Giosan8, and Timothy Ian Eglinton1 1Geological Institute, ETH Zürich, Sonneggstrasse 5, 8092 Zürich, Switzerland 2Department of Earth Sciences, Utrecht University, Heidelberglaan 2, 3584 CS Utrecht, the Netherlands 3Department of Earth Sciences, Indian Institute of Science Education and Research Kolkata, 741246 Mohanpur, West Bengal, India 4Division of Geological and Planetary Science, California Institute of Technology, 1200 East California Boulevard, Pasadena, California 91125, USA 5Institute for Geotechnical Engineering, ETH Zürich, Stefano-Franscini-Platz 3, 8093 Zürich, Switzerland 6Laboratory of Ion Beam Physics, ETH Zürich, Otto-Stern-Weg 5, 8093 Zürich, Switzerland 7Scottish Universities Environmental Research Centre AMS Laboratory, Rankine Avenue, East Kilbride, G75 0QF Glasgow, Scotland 8Geology and Geophysics Department, Woods Hole Oceanographic Institution, 86 Water Street, Woods Hole, Massachusetts 02543, USA Correspondence: Muhammed Ojoshogu Usman ([email protected]) Received: 12 January 2018 – Discussion started: 8 February 2018 Revised: 18 May 2018 – Accepted: 24 May 2018 – Published: 7 June 2018 Abstract. The modern-day Godavari River transports large sediment mineralogy, largely driven by provenance, plays an amounts of sediment (170 Tg per year) and terrestrial organic important role in the stabilization of OM during transport carbon (OCterr; 1.5 Tg per year) from peninsular India to the along the river axis, and in the preservation of OM exported Bay of Bengal. -

Suspended Sediment Transport in the Ganges-Brahmaputra
SUSPENDED SEDIMENT TRANSPORT IN THE GANGES-BRAHMAPUTRA RIVER SYSTEM, BANGLADESH A Thesis by STEPHANIE KIMBERLY RICE Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE August 2007 Major Subject: Oceanography SUSPENDED SEDIMENT TRANSPORT IN THE GANGES-BRAHMAPUTRA RIVER SYSTEM, BANGLADESH A Thesis by STEPHANIE KIMBERLY RICE Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Approved by: Co-Chairs of Committee, Beth L. Mullenbach Wilford D. Gardner Committee Members, Mary Jo Richardson Head of Department, Robert R. Stickney August 2007 Major Subject: Oceanography iii ABSTRACT Suspended Sediment Transport in the Ganges-Brahmaputra River System, Bangladesh. (August 2007) Stephanie Kimberly Rice, B.S., The University of Mississippi Co-Chairs of Advisory Committee: Dr. Beth L. Mullenbach Dr. Wilford D. Gardner An examination of suspended sediment concentrations throughout the Ganges- Brahmaputra River System was conducted to assess the spatial variability of river sediment in the world’s largest sediment dispersal system. During the high-discharge monsoon season, suspended sediment concentrations vary widely throughout different geomorphological classes of rivers (main river channels, tributaries, and distributaries). An analysis of the sediment loads in these classes indicates that 7% of the suspended load in the system is diverted from the Ganges and Ganges-Brahmaputra rivers into southern distributaries. Suspended sediment concentrations are also used to calculate annual suspended sediment loads of the main river channels. These calculations show that the Ganges carries 262 million tons/year and the Brahmaputra carries 387 million tons/year. -

Inter Linking of Rivers - a Review
International Journal of Innovations in Engineering and Technology (IJIET) http://dx.doi.org/10.21172/ijiet.144.14 Inter Linking of Rivers - a Review Harbir Singh Scientist ‘C’, CSMRS, New Delhi Abstract. The rivers in India are truly speaking not only life-line of masses but also for nature. The rivers play a very important role in the life of the People. The river system facilitate us in irrigation, potable water, cheap transportation, energy as well as a resource of living for our ever growing population. Some of the major cities of India are located at the bank of holy rivers. Proper supervision of river water is the need of the hour. Indian agriculture mainly depends upon Monsoon which is always vague in nature. Hence, there is a rigorous problem of lack of irrigation in one region and water logging in other region. Damage to crops due to deficiency and pathetic drainage facility could be managed. Depleting and declining status of water resources may be one of the most essential resource issues in the 21stcentury. The core idea of the paper is to study issues and challenges in interlinking of rivers in India and to study ecological collision of Inter-River Linking Project (IRL). Inter-River Linking Project (IRL), issues and challenges Inter-River Linking Project involves multifaceted issues and challenges related to financially viable, environmental, and social costs. I. INTRODUCTION The Inter-linking of Rivers in India proposal has a long history. During the British colonial rule during 19th century engineer Arthur Cotton proposed the plan to interlink major Indian rivers in order to hasten import and export of goods from its colony in South Asia, as well as to address water shortages and droughts in southeastern India (now Andhra Pradesh and Orissa).In 1970s, Dr.