DOCSLIB.ORG

Spatial Patterns of Institutional Innovations Within a Modernizing Society

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spatial Patterns of Institutional Innovations Within a Modernizing Society a . , .. - - - * ■ *• — — - I 72-4595. ' NWALA, Eze Ogbueri Ajoku, 1940- SPATIAL PATTERNS OF INSTITUTIONAL INNOVATIONS WITHIN A MODERNIZING SOCIETY. The Ohio State University, Ph.D., 1971 Geography University Microfilms, A XEROX Company, Ann Arbor, Michigan <0, Copyr i ght by Eze Ogbueri Ajoku Nwala 1971 THIS DISSERTATION HAS BEEN MICROFILMED EXACTLY AS RECEIVED SPATIAL PATTERNS OF INSTITUTIONAL INNOVATIONS WITHIN A MODERNIZING SOCIETY DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Eise Ogbueri Ajoku Nwala, B.A. (Hons), M.A« The Ohio State University 1971 Approved by Advj. sor Department of Geography PLEASE NOTE: Some Pages have indistinct print. Filmed as received. UNIVERSITY MICROFILMS ACKNOWLEDGMENTS Many persons have helped me by their interest, encour­ agement, criticisms and comments during the preparation of this study. They certainly merit my warm appreciation and thanks. I wish to thank Dr. L. A. Brown, my adviser, for the stimulus, comments and direction that made the logical presentation of this research possible. My thanks are extended to Dr. G. J. Demko for his keen interest, help and comments. Dr. H. L. Gauthier, Dr. K. R. Cox and Dr. R. K. Serople are thanked for encouragement and comments that helped elucidate some ideas that were hazy to the author during the study. Dr. E. J. Taaffe, Chairman, Department of Geography and the Graduate School, The Ohio State University, are deeply thanked for providing the con­ ducive working time and an award of a teaching assistant- ship that made this task a reality. The staff of the Inter-Library Loan of The Ohio State University Library are remembered. My thanks also are for Eastern Nigerians at Ohio State for their encouragement. In particular, I wish to thank Dr. E. Okechukwu Odita, Division of the History of To Late Chief Nwokogba Amadi Nwala c VITA August 5, 1940 • . Born - Egwi-Etche, Port Harcourt, Nigeria 1967 ......... B.A. (Hons), University of Durham, England 1967-1968. ........... Research Assistant, Department of Geography, University of Ottawa, Canada 1969 ......... M.A., University of Ottawa, Canada 1968-197 1 ............. Teaching Associate, Department of Geography, The Ohio State Univer­ sity, Columbus, Ohio. FIELDS OF STUDY Major Field: Geography Urban Geography. Professors L. A. Brown, R. G. Golledge and L. J. King Social/Population Geography. Professors L. A. Brown, G. J. Demko and K. R. Cox Development Geography, professors H. L. Gauthier, G. J. DemRo and R. K. Semple ( v TABLE OF CONTENTS Page ACKNOWLEDGMENTS. ............. ................ i:Li VITA ..................... .............................. v LIST OF TABLES ....................... viii LIST OF FIGURES.........................xi Chapter I. INTRODUCTION..................... 1 II. DIFFUSION STUDIES IN GEOGRAPHY.......... 7 Introduction ............................. 7 Spatial Diffusion Patterns ............. 7 Spatial Diffusion Processes. ........... Innovation Types ................ ■j’® Methodological Notes . ............. ** Overview of the Research Design..... 24 III. SETTING, DATA, VARIABLES AND HYPOTHESES . 26 Introduction ......................... 26 Setting. ................................26 Data Sources ............................34 Nature of Variables. ..............38 Urban Place Variables. 39 Administrative District Variables. .. 40 Hypotheses ......................... 41 IV. EMPIRICAL TESTS - ORIGIN TIMES OF ADOPTION.....................................45 Introduction ................... ... 45 Origin Times Adoption Test Results - Individual Central Places...... 48 vi CONTENTS (continued) Chapter Page IV. (continued) Origin Time Adoption Test Results - Administrative Districts........... 57 Summary............................... 67 V. EMPIRICAL TESTS - RATES OF ADOPTION TEST. 71 Introduction ................... 71 Rates of Adoption Results - Individual Central Places. «.............. 71 Rates of Adoption Test Results - Administrative Districts. • • • • • 79 VI. SPATIAL DIMENSIONS OF INSTITUTIONAL INNOVATION PATTERNS IN EASTERN NIGERIA. 88 Introduction ................ ••••• 88 Principal Components Results - Summary ............. 90 Secondary School Diffusion Patterns - Basic Structural Dimensions. • ... 91 Hospital Diffusion Patterns - Basic Structural Dimensions .....•• 101 Summary............. 107 VII. SUMMARY, CONCLUSIONS AND IMPLICATIONS . H I Summary and Conclusions. ........... Ill Implications for Future Research . 114 APPENDIX A. DATA SOURCES................................ 118 B. SECONDARY SCHOOL DIFFUSION IN EASTERN NIGERIA .................... H 8 BIBLIOGRAPHY 123 LIST OF TABLES TABLE Page 1. CITY SIZE DISTRIBUTIONS IN EASTERN NIGERIA. 35 2. SIMPLE CORRELATION COEFFICIENTS BET I VEEN ADOPTION TIMES OF SECONDARY SCHOOLS AND EIGHT INDEPENDENT VARIABLES (INDIVIDUAL CENTER LEVEL) ................................ 3. SIMPLE CORRELATION COEFFICIENTS BETWEEN ADOPTION TIMES OF HOSPITALS AND EIGHT INDEPENDENT VARIABLES ........................ 50 4. MULTIPLE STEPWISE REGRESSION RESULTS - ADOPTION TIMES OF SECONDARY SCHOOLS (INDIVIDUAL CENTER LEVEL) ................... 52 5. •MULTIPLE STEPWISE REGRESSION RESULTS - ADOPTION TIMES OF HOSPITALS (INDIVIDUAL CENTER LEVEL) ................................ 54 6. SIMPLE CORRELATION COEFFICIENTS BETWEEN ADOPTION TIMES OF SECONDARY SCHOOLS AND 17 INDEPENDENT VARIABLES (DISTRICT LEVEL) . 58 7. MULTIPLE STEPWISE REGRESSION RESULTS - ADOPTION TIMES OF SECONDARY SCHOOLS (ADMINISTRATIVE DISTRICT LEVEL) ............. 6* 8. COMPUTED REGRESSION RESULTS AT THE SEVENTH ORDER OF VARIABLE ENTRY ........................ 63 9. COMPUTED REGRESSION RESULTS AT THE FIFTEENTH ORDER OF VARIABLE ENTRY 65 10. SIMPLE CORRELATION COEFFICIENTS BETWEEN RATES OF DIFFUSION OF SECONDARY SCHOOLS AND EIGHT INDEPENDENT VARIABLES (INDIVIDUAL CENTER LEVEL) .............................. v• m• » TABLES (continued) TABLE Page 11. MULTIPLE STEPWISE REGRESSION RESULTS - RATES OF ADOPTION OF SECONDARY SCHOOLS (INDIVIDUAL CENTERS) ........................ 74 12. SIMPLE CORRELATION COEFFICIENTS OF RATES OF ADOPTION OF HOSPITALS AND EIGHT INDEPENDENT VARIABLES (INDIVIDUAL CENTER LEVEL)......... 76 13. MULTIPLE STEPWISE REGRESSION RESULTS - RATES OF ADOPTION OF HOSPITALS (INDIVIDUAL CENTER LEVEL)................................. 77 14. SIMPLE CORRELATION COEFFICIENTS BETWEEN RATES OF ADOPTION OF SECONDARY SCHOOLS AND SIXTEEN INDEPENDENT VARIABLES (ADMINIS­ TRATIVE DISTRICT LEVEL) ..................... 80 15. SIMPLE CORRELATION COEFFICIENTS BETWEEN RATES OF ADOPTION OF HOSPITALS AND SIXTEEN INDEPENDENT VARIABLES (ADMINISTRATIVE DISTRICT LEVEL).................................. 81 16. MULTIPLE STEPWISE REGRESSION RESULTS - RATES OF ADOPTION OF SECONDARY SCHOOLS (ADMINISTRATIVE DISTRICT LEVEL)................ 82 17. MULTIPLE STEPWISE REGRESSION RESULTS - RATES OF ADOPTION OF HOSPITALS (ADMINIS­ TRATIVE DISTRICT LEVEL)......................... 84 18. LIST OF HIGH INTERCORRELATION COEFFICIENTS AMONGST INDEPENDENT VARIABLES. , ........... 86 19. COMPONENTS OF SECONDARY SCHOOL ADOPTIONS (INDIVIDUAL CENTER LEVEL) - POPULATION- WEALTH DIMENSION, ROTATED FACTOR ONE .... 92 20. COMPONENTS OF SECONDARY SCHOOL ADOPTIONS (INDIVIDUAL CENTER LEVEL) - HIERARCHICAL DIMENSION, ROTATED FACTOR TWO ............... 96 21. COMPONENTS OF SECONDARY SCHOOL ADOPTIONS (INDIVIDUAL CENTER LEVEL) - NEIGHBORKOOD- ACCESSIBILITY DIMENSION, ROTATED FACTOR THREE............. * 98 ix TABLES (continued) TABLE Page 22. COMPONENTS OF HOSPITAL ADOPTIONS (INDIVIDUAL CENTER LEVEL) - POPULATION- WEALTH DIMENSION, ROTATED FACTOR ONE . 102 23. COMPONENTS OF HOSPITAL ADOPTIONS (INDIVIDUAL CENTER LEVEL - NEIGHBORHOOD EFFECT DIMENSION, ROTATED FACTOR TWO . 103 24. COMPONENTS OF HOSPITAL ADOPTIONS (INDIVIDUAL CENTER LEVEL) - HIERARCHICAL DIMENSION, ROTATED FACTOR THREE........... 104 x LIST OF FIGURES FIGURE Page 1. Eastern Nigeria Traditional Marketing Network................................. 27 2. Eastern Nigeria - Administrative Organisa­ tion 1900-1954 ........... * ............. 30 3. Eastern Nigeria - Administrative Provinces and Divisions 1955-1965.................. 31 4. Eastern Nigeria - Highway Transportation System 1914-1965 ......................... 33 5. Eastern Nigeria - Urban Places 1953 . • • • 36 6. Eastern Nigeria - Urban Places 1963 • • • • 37 7. Eastern Nigeria - Temporal Phases of Secondary School Adoptions ...•••• 46 8. Location of Study Centers • •••#.#•• 47 9* Residuals from Regression .................. 69 10# Rotated Factor One Scores - Economic Wealth Development Dimension ........... ®3 11# Rotated Factor Two Scores - Hierarchical Effect Dimension ........... ............. 12# Rotated Factor Three Scores - Accessibility Effect Dimension •••*•• ........... *00 13# Rotated Factor One Scores - Hospitals Economic Wealth Development Dimension • 105 xi (' CHAPTER I INTRODUCTION Diffusion studies focusing on processes and patterns have long been recognized as a major concern for research amongst the social sciences, /nthropologists, rural sociologists, economists and geographers have shown deep- seated interest in diffusion research. The result of this interdisciplinary interest has been an accumulation of an extensive literature relating to diffusion problems. Although such a massive build up of literature in diffusion studies abounds, it is, nevertheless, true to note that majority of these papers have concentrated heavily on diffusion of innovations within the highly urbanized and developed
Load more

Recommended publications
  • Citizens Wealth Platform 2017
    2017 FEDERAL CAPITAL BUDGET PULLOUT Of the States in the SOUTH-EAST Geo-Political Zone C P W Citizens Wealth Platform Citizen Wealth Platform (CWP) (Public Resources Are Made To Work And Be Of Benefit To All) 2017 FEDERAL CAPITAL BUDGET of the States in the SOUTH EAST Geo-Political Zone Compiled by VICTOR EMEJUIWE For Citizens Wealth Platform (CWP) (Public Resources Are Made To Work And Be Of Benefit To All) 2017 SOUTH EAST FEDERAL CAPITAL BUDGET PULLOUT Page 2 First Published in August 2017 By Citizens Wealth Platform C/o Centre for Social Justice 17 Yaounde Street, Wuse Zone 6, Abuja Email: [email protected] Website: www.csj-ng.org Tel: 08055070909. Blog: csj-blog.org. Twitter:@censoj. Facebook: Centre for Social Justice, Nigeria 2017 SOUTH EAST FEDERAL CAPITAL BUDGET PULLOUT Page 3 Table of Contents Foreword 5 Abia State 6 Anambra State 26 Embonyi State 46 Enugu State 60 Imo State 82 2017 SOUTH EAST FEDERAL CAPITAL BUDGET PULLOUT Page 4 Foreword In the spirit of the mandate of the Citizens Wealth Platform to ensure that public resources are made to work and be of benefit to all, we present the South East Capital Budget Pullout for the financial year 2017. This has been our tradition in the last six years to provide capital budget information to all Nigerians. The pullout provides information on federal Ministries, Departments and Agencies, names of projects, amount allocated and their location. The Economic Recovery and Growth Plan (ERGP) is the Federal Government’s blueprint for the resuscitation of the economy and its revival from recession.
    [Show full text]
  • Article Download
    wjert, 2018, Vol. 4, Issue 6, 95 -102. Original Article ISSN 2454-695X Ibeje etWorld al. Journal of Engineering World Journal ofResearch Engineering and Research Tech andnology Technology WJERT www.wjert.org SJIF Impact Factor: 5.218 IMPACTS OF LAND USE ON INFILTRATION A. O. Ibeje*1, J. C. Osuagwu2 and O. R. Onosakponome2 1Department of Civil Engineering, Imo State University, P.M.B. 2000, Owerri, Nigeria. 2Department of Civil Engineering, Federal University of Technology, Owerri, Nigeria. Article Received on 12/09/2018 Article Revised on 03/10/2018 Article Accepted on 24/10/2018 ABSTRACT *Corresponding Author Land use can affect natural ecological processes such as infiltration. A. O. Ibeje There are many land uses applied at Ikeduru L.G.A. in Imo State, Department of Civil Nigeria, thus, the area is selected as a case study. The objective of Engineering, Imo State University, P.M.B. 2000, study is to determine the effects of land use on infiltration by three Owerri, Nigeria. different land use types; 34 of them are in farmlands, 34 in Bamboo field and 32 in forestlands. Within each land use type, multiple regression are used to determine degree of association between the rates of infiltration, moisture content, porosity, bulk density and particle sizes. Non-parametric Kruskal-Wallis analysis of variance is used to determine whether significant differences in infiltration rates existed between different land uses. The mean steady state infiltration rate of farmlands, bamboo fields and forestland are 1.98 cm/h, 2.44cm/h and 2.43cm/h respectively. The regression model shows that infiltration rate decreases with increase in moisture content and bulk density but increases with the increase of soil particle sizes and porosity.
    [Show full text]
  • DETERMINATION of the ERODIBILITY STATUS of SOME SOILS in IKEDURU LOCAL GOVERNMENT AREA of IMO STATE, NIGERIA Chukwuocha N., *Amangabara G.T., and Amaechi C
    International Journal of Geology, Earth and Environmental Sciences ISSN: 2277-2081 (Online) An Open Access, Online International Journal Available at http://www.cibtech.org/jgee.htm 2014 Vol. 4 (1) January-April, pp. 236-243/Chukwuocha et al. Research Article DETERMINATION OF THE ERODIBILITY STATUS OF SOME SOILS IN IKEDURU LOCAL GOVERNMENT AREA OF IMO STATE, NIGERIA Chukwuocha N., *Amangabara G.T., and Amaechi C. 1Department of Environmental Technology, Federal University of Technology, PMB 1526 Owerri *Author for Correspondence ABSTRACT Determination of soil erodibility status in four selected communities of Ikeduru LGA was conducted. Soil samples were collected randomly from Cassava farm, Bamboo field, Fallow land and sparse grassland and were analysed for moisture content, particle size distribution, textural class, organic matter content, permeability and aggregate structure using oven drying method, sieve analysis, triangular chart, and permeability/soil type table. Laboratory results were subjected to statistical analyses. Narrow variation was seen in all the particle size distribution (ranged from 25.10 – 35.15) with samples from sparse grass land vegetation having the least value (35.20), samples from cassava farm and bamboo field had their values as 35.15 and 29.40 respectively. The clay, silt and MC had a negative non-significant relationship with the erodibility status with values of correlation -.412, -.532 and -.836 respectively. While sand percentage content had a positive non significant relationship with erodibility factor K having the values of .670. OMC percentage content had a high positive significant relationship with erodibility factor K, with the value of correlation as 1.000**. There was a high level of significance between clay, silt, sand, OMC, and MC with values of correlation as -.753**, -.714**, -.831**, and .955** respectively.
    [Show full text]
  • Employment Creation and Constraints to Fish Farming in the Niger Delta Region of Nigeria
    Research Article Int J Environ Sci Nat Res Volume 23 Issue 2 - January 2020 DOI: 10.19080/IJESNR.2020.23.556108 Copyright © All rights are reserved by Robert Ugochukwu Onyeneke Employment Creation and Constraints to Fish Farming in the Niger Delta Region of Nigeria Robert Ugochukwu Onyeneke1*, Felix Abinotam Iruo2 and Christopher Chiedozie Eze3 1Department of Agriculture (Agricultural Economics and Extension Programme), Alex Ekwueme Federal University Ndufu-Alike, Nigeria 2Department of Agricultural Economics and Rural Sociology, Niger Delta University, Nigeria 3Department of Agricultural Economics, Federal University of Technology Owerri, Nigeria Submission: Published: *Corresponding December author: 16, 2019; January 06, 2020 Robert Ugochukwu Onyeneke, Department of Agriculture (Agricultural Economics and Extension Programme), Alex Ekwueme Federal University Ndufu-Alike, Ebonyi State, Nigeria Abstract The study analysed employment creation and constraints to fish farming in Nigeria’s Niger Delta region. A combination of purposive and multistage sampling techniques was used in selecting 360 fish farmers for this study while a structured questionnaire was designed and used for data collection. Our results show that a total of 3,360 jobs were generated from fish production, fish marketing, processing and distribution as well as inputs distribution. Farmers used the income realized from fish farming to acquire assets such as land, cars, motorcycles, buildings and household facilities and provision of education to their children. High cost of feed and other inputs (92.2%) was the major challenge facing fish farming.Keywords: Research and technology on alternative cost-effective sources of feed and other inputs in the region be explored. Fish farming; Niger delta; Employment creation; constraints Introduction determined: neglected but important sector.
    [Show full text]
  • Imo State Government of Nigeria Revised Budget 2020 Summary of Capital Expenditure
    IMO STATE GOVERNMENT OF NIGERIA REVISED BUDGET 2020 SUMMARY OF CAPITAL EXPENDITURE HEAD SUB-SECTORS APPROVED APPROVED REVISED COVID-19 BUDGET BUDGET BUDGET RESPONSIVE 2019 2020 2020 ECONOMIC SECTOR 82,439,555,839 63,576,043,808 20,555,468,871 2,186,094,528 SOCIAL SERVICES SECTOR 50,399,991,403 21,139,598,734 7,190,211,793 3,043,134,650 GENERAL ADMIN: (MDA'S) 72,117,999,396 17,421,907,270 12,971,619,207 1,150,599,075 GENERAL ADMIN: (GOVT COUNTERPART FUND PAYMENTS) 9,690,401,940 4,146,034,868 48,800,000 - GENERAL ADMIN: (GOVT TRANSFER - ISOPADEC) - - 4,200,000,000 - GRAND TOTAL CAPITAL EXPENDITURE 214,647,948,578 106,283,584,680 44,966,099,871 6,379,828,253 1of 1 IMO STATE GOVERNMENT OF NIGERIA IMO STATE GOVERNMENT OF NIGERIA REVISED BUDGET 2020 MINISTERIAL SUMMARY OF CAPITAL EXPENDITURE ECONOMIC SECTOR APPROVED 2019 APPROVED 2020 REVISED 2020 COVID-19 RESPONSIVE O414 MINISTRY OF AGRICULTURE AND FOOD SECURITY 1,499,486,000 2,939,000,000 1,150,450,000 - 0 AGRIC & FOOD SECURITY 1,499,486,000 0414-2 MINISTRY OF LIVESTOCK DEVELOPMENT 1,147,000,000 367,000,000 367,000,000 - 0 LIVESTOCK 1,147,000,000 697000000 1147000000 0414-1 MINISTRY OF ENVIRONMENT AND NATURAL RESOURCES 13,951,093,273 1,746,000,000 620,000,000 - 0 MINISTRY OF ENVIRONMENT 13951093273 450000000 O415 MINISTRY OF COMMERCE AND INDUSTRY 7,070,700,000 2,650,625,077 1,063,000,000 - -5,541,800,000 MINISTRY OF COMMERCE, INDUSTRY AND ENTREPRENEURSHIP1528900000 0419-2 MINISTRY OF WATER RESOURCES 2,880,754,957 2,657,000,000 636,869,000 - 1,261,745,492 MINISTRY OF PUBLIC UTILITIES 4,142,500,449
    [Show full text]
  • A Study of Chikum Microfinance Bank Limited
    University of San Diego Digital USD Dissertations Theses and Dissertations 2020-08-31 Institutional Logics and the Double Bottom Line: A Study of Chikum Microfinance Bank Limited Daniel Anyanwu University of San Diego Follow this and additional works at: https://digital.sandiego.edu/dissertations Part of the Entrepreneurial and Small Business Operations Commons, and the Leadership Studies Commons Digital USD Citation Anyanwu, Daniel, "Institutional Logics and the Double Bottom Line: A Study of Chikum Microfinance Bank Limited" (2020). Dissertations. 183. https://digital.sandiego.edu/dissertations/183 This Dissertation: Open Access is brought to you for free and open access by the Theses and Dissertations at Digital USD. It has been accepted for inclusion in Dissertations by an authorized administrator of Digital USD. For more information, please contact [email protected]. University of San Diego Digital USD Dissertations Theses and Dissertations 2020-08-31 Institutional Logics and the Double Bottom Line: A Study of Chikum Microfinance Bank Limited Daniel Anyanwu Follow this and additional works at: https://digital.sandiego.edu/dissertations Part of the Entrepreneurial and Small Business Operations Commons, and the Leadership Studies Commons INSTITUTIONAL LOGICS AND THE DOUBLE BOTTOM LINE: A STUDY OF CHIKUM MICROFINANCE BANK LIMITED by Daniel Amanze Anyanwu A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy August 2020 Dissertation Committee Hans Peter Schmitz, PhD Robert Donmoyer,
    [Show full text]
  • New Projects Inserted by Nass
    NEW PROJECTS INSERTED BY NASS CODE MDA/PROJECT 2018 Proposed Budget 2018 Approved Budget FEDERAL MINISTRY OF AGRICULTURE AND RURAL SUPPLYFEDERAL AND MINISTRY INSTALLATION OF AGRICULTURE OF LIGHT AND UP COMMUNITYRURAL DEVELOPMENT (ALL-IN- ONE) HQTRS SOLAR 1 ERGP4145301 STREET LIGHTS WITH LITHIUM BATTERY 3000/5000 LUMENS WITH PIR FOR 0 100,000,000 2 ERGP4145302 PROVISIONCONSTRUCTION OF SOLAR AND INSTALLATION POWERED BOREHOLES OF SOLAR IN BORHEOLEOYO EAST HOSPITALFOR KOGI STATEROAD, 0 100,000,000 3 ERGP4145303 OYOCONSTRUCTION STATE OF 1.3KM ROAD, TOYIN SURVEYO B/SHOP, GBONGUDU, AKOBO 0 50,000,000 4 ERGP4145304 IBADAN,CONSTRUCTION OYO STATE OF BAGUDU WAZIRI ROAD (1.5KM) AND EFU MADAMI ROAD 0 50,000,000 5 ERGP4145305 CONSTRUCTION(1.7KM), NIGER STATEAND PROVISION OF BOREHOLES IN IDEATO NORTH/SOUTH 0 100,000,000 6 ERGP445000690 SUPPLYFEDERAL AND CONSTITUENCY, INSTALLATION IMO OF STATE SOLAR STREET LIGHTS IN NNEWI SOUTH LGA 0 30,000,000 7 ERGP445000691 TOPROVISION THE FOLLOWING OF SOLAR LOCATIONS: STREET LIGHTS ODIKPI IN GARKUWARI,(100M), AMAKOM SABON (100M), GARIN OKOFIAKANURI 0 400,000,000 8 ERGP21500101 SUPPLYNGURU, YOBEAND INSTALLATION STATE (UNDER OF RURAL SOLAR ACCESS STREET MOBILITY LIGHTS INPROJECT NNEWI (RAMP)SOUTH LGA 0 30,000,000 9 ERGP445000692 TOSUPPLY THE FOLLOWINGAND INSTALLATION LOCATIONS: OF SOLAR AKABO STREET (100M), LIGHTS UHUEBE IN AKOWAVILLAGE, (100M) UTUH 0 500,000,000 10 ERGP445000693 ANDEROSION ARONDIZUOGU CONTROL IN(100M), AMOSO IDEATO - NCHARA NORTH ROAD, LGA, ETITI IMO EDDA, STATE AKIPO SOUTH LGA 0 200,000,000 11 ERGP445000694
    [Show full text]
  • Updated-Imo-ESMF.Pdf
    FEDERAL GOVERNMENT OF NIGERIA Public Disclosure Authorized SECOND RURAL ACCESS AND MOBILITY PROJECT (RAMP II) ENVIRONMENTAL AND SOCIAL MANAGEMENT FRAMEWORK (ESMF) Public Disclosure Authorized Public Disclosure Authorized IN IMO STATES, NIGERIA. BY FEDERAL MINISTRY OF AGRICULTURE & RURAL DEVELOPMENT FEDERAL PROJECT MANAGEMENT UNIT (FPMU) SECOND RURAL ACCESS & MOBILITY PROJECT (RAMP 2) NAIC HOUSE, PLOT 590, AO CENTRAL AREA, ABUJA. Public Disclosure Authorized NOVEMBER, 2016 Federal Project Management Unit (FPMU), Rural Access & Mobility Project (RAMP), September, 2016 Environmental and Social Management Framework (ESMF) for RAMP II States (Adamawa, Enugu, Niger, Osun and Imo) TABLE OF CONTENTS Content Page Title Page i Table of Contents ii List of Tables iv List of Figures iv List of Boxes iv List of Maps v List of Plates v List of Appendices v List of Acronyms vi Executive Summary ix CHAPTER ONE: BACKGROUND AND INTRODUCTION 1 1.0 Project Background 1 1.1 Project Beneficiaries 1 1.2 The RAMP II Project 1 1.3 Purpose of the ESMF 2 CHAPTER TWO:POLICY, LEGAL AND REGULATORY FRAME WORK 3 2.0 Introduction 3 2.1 Institutional Arrangement for ESMF 3 2.2 World Bank’s Environmental and Social Guidelines 5 2.3 Nigeria EA Guidelines and World Bank EA Guidelines 6 CHAPTER THREE: PROJECT DESCRIPTION 9 3.0 Introduction 9 3.1 Project Components 9 3.2 Applicable Safeguard Policies 9 3.3 Road Selection in Imo State 10 3.4 Analysis of Institutional Capacity 13 CHAPTER FOUR: DESCRIPTIONS OF BASELINE CONDITIONS OF STATES 14 4.0 Introduction 14 4.1 Project location
    [Show full text]
  • National Assembly 260 2013 Appropriation
    FEDERAL GOVERNMENT OF NIGERIA 2013 BUDGET SUMMARY FEDERAL MINISTRY OF WATER RESOURCES TOTAL TOTAL PERSONNEL TOTAL CODE MDA OVERHEAD TOTAL RECURRENT TOTAL CAPITAL COST ALLOCATION COST =N= =N= =N= =N= =N= FEDERAL MINISTRY OF WATER RESOURCES - 0252001001 1,062,802,556 434,615,687 1,497,418,243 28,714,910,815 30,212,329,058 HQTRS 0252037001 ANAMBRA/ IMO RBDA 455,494,870 69,652,538 525,147,408 7,223,377,629 7,748,525,037 252038001 BENIN/ OWENA RBDA 310,381,573 48,517,004 358,898,577 2,148,547,575 2,507,446,152 0252039001 CHAD BASIN RBDA 349,481,944 66,930,198 416,412,142 2,090,796,556 2,507,208,698 0252040001 CROSS RIVER RBDA 336,692,834 69,271,822 405,964,656 5,949,000,000 6,354,964,656 0252051001 GURARA WATER MANAGEMENT AUTHORITY 17,112,226 70,346,852 87,459,078 167,000,000 254,459,078 0252041001 HADEJIA-JAMAļARE RBDA 384,683,182 53,037,247 437,720,429 5,322,607,552 5,760,327,981 0252042001 LOWER BENUE RBDA 305,996,666 49,183,926 355,180,592 4,684,200,000 5,039,380,592 0252043001 LOWER NIGER RBDA 510,037,910 66,419,289 576,457,199 5,452,950,000 6,029,407,199 0252044001 NIGER DELTA RBDA 509,334,321 77,714,503 587,048,824 4,382,640,000 4,969,688,824 NIGERIA INTEGRATED WATER MANAGEMENT 0252050001 143,297,122 89,122,355 232,419,477 154,000,000 386,419,477 COMMISSION NATIONAL WATER RESOURCES INSTITUTE- 0252049001 266,646,342 40,532,007 307,178,349 403,000,000 710,178,349 KADUNA 0252045001 OGUN/ OSUN RBDA 387,437,686 79,556,978 466,994,664 3,500,153,045 3,967,147,709 0252046001 SOKOTO RIMA RBDA 431,782,730 83,609,292 515,392,022 6,827,983,001 7,343,375,023
    [Show full text]
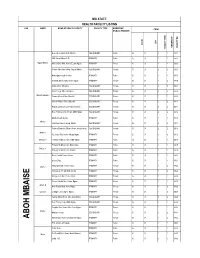
  • List of Coded Health Facilities in Imo State.Pdf
    IMO STATE HEALTH FACILITY LISTING LGA WARD NAME OF HEALTH FACILITY FACILITY TYPE OWNERSHIP CODE (PUBLIC/ PRIVATE) LGA STATE OWNERSHIP FACILITY NO FACILITY FACILITY TYPE FACILITY General Hospital Aboh Mbaise SECONDARY Public 16 01 2 1 0001 IWC Aboh Mbaise HQ PRIMARY Public 16 01 1 1 0002 Nguru Nweke Mrs.S. Osuji Mat. Home Ezuhu Nguru PRIMARY Private 16 01 1 2 0003 County Specialist Hosp. Nguru Mbaise SECONDARY Private 16 01 2 2 0004 Nkworgwu Health Centre PRIMARY Public 16 01 1 1 0005 Kenneth Memo Mat. Home Nguru PRIMARY Private 16 01 1 2 0006 Arugo Clinic Oboama SECONDARY Private 16 01 2 2 0007 Avian Hosp. Oboetiti Nguru SECONDARY Private 16 01 2 2 0008 Nguru Nwankwo Panma Memo Clinic Oboetiti SECONDARY Private 16 01 2 2 0009 Chiloko Memo Clinic Oboetiti SECONDARY Private 16 01 2 2 0010 Regina Caeli Umuoji Hosp (mission) SECONDARY Private 16 01 2 2 0011 Holy Trinity Comm. Hosp. Obibi Nguru SECONDARY Private 16 01 2 2 0012 Mbutu Health Centre PRIMARY Public 16 01 1 1 0013 Mbutu I Christian Mission Hosp. Mbutu SECONDARY Private 16 01 2 2 0014 Sydney Ewunonu Memo Hosp. Avutu mbutu SECONDARY Private 16 01 2 2 0015 Mbutu II St. Judes Mat. Home Mbutu Ngwa PRIMARY Private 16 01 1 2 0016 Mbutu IV Primary Health Centre Isiala Mbutu PRIMARY Public 16 01 1 1 0017 Primary Health Centre Nkwuogwu PRIMARY Public 16 01 1 1 0018 Mbutu V Primary Health Centre Umuhu PRIMARY Public 16 01 1 1 0019 Basic Health Centre Uvuru PRIMARY Public 16 01 1 1 0020 Uvuru Disp.
    [Show full text]
  • The Effects of “Permanent Migration” on the Economy of Owerri Province, Eastern Nigeria, 1950-1967
    Asian Journal of Social Sciences & Humanities Vol. 4(1) February 2015 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ The Effects of “Permanent Migration” on the Economy of Owerri Province, Eastern Nigeria, 1950-1967 Austine Uchechukwu Igwe1, Nwachukwu Obiakor2 Department of History & International Studies, Nnamdi Azikiwe University, Awka, NIGERIA. [email protected] ABSTRACT This paper focuses on internally generated economically motivated or modern migrations within Eastern Nigeria in the twentieth century, especially from 1950 to 1967 and its effects on the economy of Owerri Province. From the dawn of colonial rule in Nigeria, modern migration was characterized by rural-urban drift in diverse forms. It emerged as a consequence of the development of a money economy, which created employment opportunities in the new centres of development. During the period, migrant labour became coterminous with ‘wage’ labour because of the intrusion of people from the rural areas to the new centres of commerce for the purpose of wage employment. However, as from the end of the Second World War, “permanent migration” began to manifest in Eastern Nigeria
    [Show full text]
  • April 2011: Combating the Nigerian Security Challenge
    Journal of Policy and Development Studies Vol. 9, No. 3, May 2015 ISSN: 157-9385 Website: www.arabianjbmr.com/JPDS_index.php APRIL 2011: COMBATING THE NIGERIAN SECURITY CHALLENGE Bar. (Mrs) Adeline Idike. A Eme, Okechukwu Innocent [email protected] Department of Public Administration, And Local Government Studies University of Nigeria, Nsukka Abstract The rising wave of violence in the run up to the April polls calls for concerted efforts from all stake holders to stem the tide of the critical election are not to be threatened or marred. Across the polity, violent conflicts are raising fresh concerns on the prospects of smith conduct of the polls which are less than two months away. In Amaimo, Ikeduru Local Government Area of Imo State, recently, unknown gun men disrupted the senatorial campaign rally of the Action congress of Nigeria. When the dust neared, an ACN Stalwart, Dr Charles Anokwa was discovered missing. There have also been reports of violence in Gboko, Benue State and Bayelsa State, between rival political parties. Also, on February 25, 2010, unexploded bombs were recovered at the VIP pavilion during the flag-off of campaign for re-election of Government Sullivan Chime of Enugu State. It is significant to up this undesirable trend in the bud before it becomes the hallmark of the coming elections. The paper identifies the absence and lack of democratic norms among politicians and the politics of winner takes all with scant regard for service delivery to the populace has enthroned a do or die” political culture in which contestants are determined to win at costs, and what ever means, fair or foul are the major threats to April 2011 elections.
    [Show full text]