Ohm's and Kirchhoff's Circuit Laws Abstract Introduction and Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Topic 0991 Electrochemical Units Electric Current the SI Base
Topic 0991 Electrochemical Units Electric Current The SI base electrical unit is the AMPERE which is that constant electric current which if maintained in two straight parallel conductors of infinite length and of negligible circular cross section and placed a metre apart in a vacuum would produce between these conductors a force equal to 2 x 10-7 newton per metre length. It is interesting to note that definition of the Ampere involves a derived SI unit, the newton. Except in certain specialised applications, electric currents of the order ‘amperes’ are rare. Starter motors in cars require for a short time a current of several amperes. When a current of one ampere passes through a wire about 6.2 x 1018 electrons pass a given point in one second [1,2]. The coulomb (symbol C) is the electric charge which passes through an electrical conductor when an electric current of one A flows for one second. Thus [C] = [A s] (a) Electric Potential In order to pass an electric current thorough an electrical conductor a difference in electric potential must exist across the electrical conductor. If the energy expended by a flow of one ampere for one second equals one Joule the electric potential difference across the electrical conductor is one volt [3]. Electrical Resistance and Conductance If the electric potential difference across an electrical conductor is one volt when the electrical current is one ampere, the electrical resistance is one ohm, symbol Ω [4]. The inverse of electrical resistance , the conductance, is measured using the unit siemens, symbol [S]. -

The Decibel Scale R.C
The Decibel Scale R.C. Maher Fall 2014 It is often convenient to compare two quantities in an audio system using a proportionality ratio. For example, if a linear amplifier produces 2 volts (V) output amplitude when its input amplitude is 100 millivolts (mV), the voltage gain is expressed as the ratio of output/input: 2V/100mV = 20. As long as the two quantities being compared have the same units--volts in this case--the proportionality ratio is dimensionless. If the proportionality ratios of interest end up being very large or very small, such as 2x105 and 2.5x10-4, manipulating and interpreting the results can become rather unwieldy. In this situation it can be helpful to compress the numerical range by taking the logarithm of the ratio. It is customary to use a base-10 logarithm for this purpose. For example, 5 log10(2x10 ) = 5 + log10(2) = 5.301 and -4 log10(2.5x10 ) = -4 + log10(2.5) = -3.602 If the quantities in the proportionality ratio both have the units of power (e.g., 2 watts), or intensity (watts/m ), then the base-10 logarithm log10(power1/power0) is expressed with the unit bel (symbol: B), in honor of Alexander Graham Bell (1847 -1922). The decibel is a unit representing one tenth (deci-) of a bel. Therefore, a figure reported in decibels is ten times the value reported in bels. The expression for a proportionality ratio expressed in decibel units (symbol dB) is: 10 푝표푤푒푟1 10 Common Usage 푑퐵 ≡ ∙ 푙표푔 �푝표푤푒푟0� The power dissipated in a resistance R ohms can be expressed as V2/R, where V is the voltage across the resistor. -

A HISTORICAL OVERVIEW of BASIC ELECTRICAL CONCEPTS for FIELD MEASUREMENT TECHNICIANS Part 1 – Basic Electrical Concepts
A HISTORICAL OVERVIEW OF BASIC ELECTRICAL CONCEPTS FOR FIELD MEASUREMENT TECHNICIANS Part 1 – Basic Electrical Concepts Gerry Pickens Atmos Energy 810 Crescent Centre Drive Franklin, TN 37067 The efficient operation and maintenance of electrical and metal. Later, he was able to cause muscular contraction electronic systems utilized in the natural gas industry is by touching the nerve with different metal probes without substantially determined by the technician’s skill in electrical charge. He concluded that the animal tissue applying the basic concepts of electrical circuitry. This contained an innate vital force, which he termed “animal paper will discuss the basic electrical laws, electrical electricity”. In fact, it was Volta’s disagreement with terms and control signals as they apply to natural gas Galvani’s theory of animal electricity that led Volta, in measurement systems. 1800, to build the voltaic pile to prove that electricity did not come from animal tissue but was generated by contact There are four basic electrical laws that will be discussed. of different metals in a moist environment. This process They are: is now known as a galvanic reaction. Ohm’s Law Recently there is a growing dispute over the invention of Kirchhoff’s Voltage Law the battery. It has been suggested that the Bagdad Kirchhoff’s Current Law Battery discovered in 1938 near Bagdad was the first Watts Law battery. The Bagdad battery may have been used by Persians over 2000 years ago for electroplating. To better understand these laws a clear knowledge of the electrical terms referred to by the laws is necessary. Voltage can be referred to as the amount of electrical These terms are: pressure in a circuit. -

The ST System of Units Leading the Way to Unification
The ST system of units Leading the way to unification © Xavier Borg B.Eng.(Hons.) - Blaze Labs Research First electronic edition published as part of the Unified Theory Foundations (Feb 2005) [1] Abstract This paper shows that all measurable quantities in physics can be represented as nothing more than a number of spatial dimensions differentiated by a number of temporal dimensions and vice versa. To convert between the numerical values given by the space-time system of units and the conventional SI system, one simply multiplies the results by specific dimensionless constants. Once the ST system of units presented here is applied to any set of physics parameters, one is then able to derive all laws and equations without reference to the original theory which presented said relationship. In other words, all known principles and numerical constants which took hundreds of years to be discovered, like Ohm's Law, energy mass equivalence, Newton's Laws, etc.. would simply follow naturally from the spatial and temporal dimensions themselves, and can be derived without any reference to standard theoretical background. Hundreds of new equations can be derived using the ST table included in this paper. The relation between any combination of physical parameters, can be derived at any instant. Included is a step by step worked example showing how to derive any free space constant and quantum constant. 1 Dimensions and dimensional analysis One of the most powerful mathematical tools in science is dimensional analysis. Dimensional analysis is often applied in different scientific fields to simplify a problem by reducing the number of variables to the smallest number of "essential" parameters. -

Resistor Selection Application Notes Resistor Facts and Factors
Resistor Selection Application Notes RESISTOR FACTS AND FACTORS A resistor is a device connected into an electrical circuit to resistor to withstand, without deterioration, the temperature introduce a specified resistance. The resistance is measured in attained, limits the operating temperature which can be permit- ohms. As stated by Ohm’s Law, the current through the resistor ted. Resistors are rated to dissipate a given wattage without will be directly proportional to the voltage across it and inverse- exceeding a specified standard “hot spot” temperature and the ly proportional to the resistance. physical size is made large enough to accomplish this. The passage of current through the resistance produces Deviations from the standard conditions (“Free Air Watt heat. The heat produces a rise in temperature of the resis- Rating”) affect the temperature rise and therefore affect the tor above the ambient temperature. The physical ability of the wattage at which the resistor may be used in a specific applica- tion. SELECTION REQUIRES 3 STEPS Simple short-cut graphs and charts in this catalog permit rapid 1.(a) Determine the Resistance. determination of electrical parameters. Calculation of each (b) Determine the Watts to be dissipated by the Resistor. parameter is also explained. To select a resistor for a specific application, the following steps are recommended: 2.Determine the proper “Watt Size” (physical size) as controlled by watts, volts, permissible temperatures, mounting conditions and circuit conditions. 3.Choose the most suitable kind of unit, including type, terminals and mounting. STEP 1 DETERMINE RESISTANCE AND WATTS Ohm’s Law Why Watts Must Be Accurately Known 400 Stated non-technically, any change in V V (a) R = I or I = R or V = IR current or voltage produces a much larger change in the wattage (heat to be Ohm’s Law, shown in formula form dissipated by the resistor). -

The International System of Units (SI)
NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303. -

Supplementary Notes on Natural Units Units
Physics 8.06 Feb. 1, 2005 SUPPLEMENTARY NOTES ON NATURAL UNITS These notes were prepared by Prof. Jaffe for the 1997 version of Quantum Physics III. They provide background and examples for the material which will be covered in the first lecture of the 2005 version of 8.06. The primary motivation for the first lecture of 8.06 is that physicists think in natural units, and it’s about time that you start doing so too. Next week, we shall begin studying the physics of charged particles mov- ing in a uniform magnetic field. We shall be lead to consider Landau levels, the integer quantum hall effect, and the Aharonov-Bohm effect. These are all intrinsically and profoundly quantum mechanical properties of elemen- tary systems, and can each be seen as the starting points for vast areas of modern theoretical and experimental physics. A second motivation for to- day’s lecture on units is that if you were a physicist working before any of these phenomena had been discovered, you could perhaps have predicted im- portant aspects of each of them just by thinking sufficiently cleverly about natural units. Before getting to that, we’ll learn about the Chandrasekhar mass, namely the limiting mass of a white dwarf or neutron star, supported against collapse by what one might loosely call “Pauli pressure”. There too, natural units play a role, although it is too much to say that you could have predicted the Chandrasekhar mass only from dimensional analysis. What is correct is the statement that if you understood the physics well enough to realize 2 that Mchandrasekhar ∝ 1/mproton, then thinking about natural units would have been enough to get you to Chandrasekhar’s result. -

Approximate Molecular Electronic Structure Methods
APPROXIMATE MOLECULAR ELECTRONIC STRUCTURE METHODS By CHARLES ALBERT TAYLOR, JR. A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY UNIVERSITY OF FLORIDA 1990 To my grandparents, Carrie B. and W. D. Owens ACKNOWLEDGMENTS It would be impossible to adequately acknowledge all of those who have contributed in one way or another to my “graduate school experience.” However, there are a few who have played such a pivotal role that I feel it appropriate to take this opportunity to thank them: • Dr. Michael Zemer for his enthusiasm despite my more than occasional lack thereof. • Dr. Yngve Ohm whose strong leadership and standards of excellence make QTP a truly unique environment for students, postdocs, and faculty alike. • Dr. Jack Sabin for coming to the rescue and providing me a workplace in which to finish this dissertation. I will miss your bookshelves which I hope are back in order before you read this. • Dr. William Weltner who provided encouragement and seemed to have confidence in me, even when I did not. • Joanne Bratcher for taking care of her boys and keeping things running smoothly at QTP-not to mention Sanibel. Of course, I cannot overlook those friends and colleagues with whom I shared much over the past years: • Alan Salter, the conservative conscience of the clubhouse and a good friend. • Bill Parkinson, the liberal conscience of the clubhouse who, along with his family, Bonnie, Ryan, Danny, and Casey; helped me keep things in perspective and could always be counted on for a good laugh. -

A) B) C) D) 1. Which Is an SI Unit for Work Done on an Object? A) Kg•M/S
1. Which is an SI unit for work done on an object? 10. Which is an acceptable unit for impulse? A) B) A) N•m B) J/s C) J•s D) kg•m/s C) D) 11. Using dimensional analysis, show that the expression has the same units as acceleration. [Show all the 2. Which combination of fundamental units can be used to express energy? steps used to arrive at your answer.] A) kg•m/s B) kg•m2/s 12. Which quantity and unit are correctly paired? 2 2 2 C) kg•m/s D) kg•m /s A) 3. A joule is equivalent to a B) A) N•m B) N•s C) N/m D) N/s C) 4. A force of 1 newton is equivalent to 1 A) B) D) C) D) 13. Which two quantities are measured in the same units? 5. Which two quantities can be expressed using the same A) mechanical energy and heat units? B) energy and power A) energy and force C) momentum and work B) impulse and force D) work and power C) momentum and energy 14. Which is a derived unit? D) impulse and momentum A) meter B) second 6. Which pair of quantities can be expressed using the same C) kilogram D) Newton units? 15. Which combination of fundamental unit can be used to A) work and kinetic energy express the weight of an object? B) power and momentum A) kilogram/second C) impulse and potential energy B) kilogram•meter D) acceleration and weight C) kilogram•meter/second 7. -

CTS-Prep Workshop II Ohm's Law, Impedance and Decibels Italy, April
CTS-Prep Workshop II Ohm’s Law, Impedance and Decibels Italy, April 2020 Jose Mozota CTS, CTS-I 1 © 2017 AVIXA Goals • Review Ohm’s Law - Calculate V, I, R and P - Understand Bus Power in AV systems • Calculate Speaker Systems Impedance (Z) • Understand Impedance matching with amplifiers • Review the concept of Decibel • Understand Decibel calculations • Review Speaker configurations 2 © 2017 AVIXA Circuits Circuits have: - Source - Load - Conductor 3 © 2017 AVIXA Ohm's Law V = I * R V (voltage) - volts I (current) - amperes R (resistance) - ohms 4 © 2017 AVIXA Introduction to Ohm's Law • Expresses the relationships between Voltage (V), Current (I) and Resistance (R) in an electrical circuit V = I * R • Helps calculate the Power (P) in a circuit P = I * V P = V2 /R P = I2 * R • If you know any 2 values, you can find the third one. 5 © 2017 AVIXA Current and Voltage • Expressed in amps by the symbol “I” • The force that causes the electrons to - The flow of electrons in a circuit flow. - In a DC circuit the flow is in one - Expressed in Volts or V (or E, Electromotive Force) direction back to source - Mic level .002V - In an AC circuit the flow reverses - Line level 0.316V (consumer) or periodically. 1.23V(pro) • I = V / R - Loudspeaker level up to 100V • V = I * R 6 © 2017 AVIXA Resistance • The opposition to the flow of electrons - Expressed in ohms (O) and by the symbol R - Applies to DC (e.g. battery) - For AC is called Impedance (Z), to be discussed later • R = V / I 7 © 2017 AVIXA Activity: Ohm's Law Calculations Calculate the current in a circuit where the voltage is 2V and resistance is 8 ohms. -
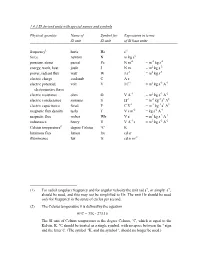
1.4.3 SI Derived Units with Special Names and Symbols
1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.