DOCSLIB.ORG

Measuring Relative Accuracy of Malware Detectors in the Absence of Ground Truth

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measuring Relative Accuracy of Malware Detectors in the Absence of Ground Truth Milcom 2018 Track 3 - Cyber Security and Trusted Computing Measuring Relative Accuracy of Malware Detectors in the Absence of Ground Truth John Charlton Pang Du Jin-Hee Cho Shouhuai Xu Depart. of Computer Science Depart. of Statistics Depart. of Computer Science Depart. of Computer Science UT San Antonio Virginia Tech Virginia Tech UT San Antonio Abstract—In this paper, we measure the relative accuracy of assumptions that were made in [4]. Although the relative accu- malware detectors in the absence of ground truth regarding the racy of malware detectors is weaker than the absolute accuracy, quality of malware detectors (i.e., the detection accuracy) or the it is still useful in regards to comparing malware detectors. class of sample files, (i.e., malicious or benign). In particular, we are interested in measuring the ordinal scale of malware Therefore, this paper aims at answering the following research detectors in the absence of the ground truth of their actual question: “How can we rank the accuracy of malware detectors detection quality. To this end, we propose an algorithm to in the absence of ground truth?” estimate the relative accuracy of the malware detectors. Based This work has the following key contributions: (i) This on synthetic data with known ground truth, we characterize study offers a method to formulate how to estimate the when the proposed algorithm leads to accurately estimating the relative accuracy of the malware detectors. We show the relative accuracy of malware detectors. This method can be measured relative accuracy of real-world malware detectors using used when one needs to choose one malware detector over our proposed algorithm based on a real dataset consisting of 10.7 others; and (ii) The proposed algorithm measuring the relative million files and 62 malware detectors, obtained from VirusTotal. detection accuracy of a malware detector is validated based on a real world malware dataset consisting of 62 detectors, given Index Terms—Malware detection, security metrics, security measurement, ground truth, estimation, statistical estimators. synthetic data with known ground truth values. The rest of the paper is organized as follows. Section II pro- vides the overview of the related state-of-the-art approaches. I. INTRODUCTION Section III presents a problem statement and our proposed Measuring security metrics is a vital but challenging open methodology to solve the given problem. Section IV describes research problem that has not been well addressed. The major the experimental setup and results, with the discussion of key problems in measuring security metrics are two-fold: (1) what findings. Section V concludes the paper and suggests future to measure, which questions how to define new, useful security research directions. metrics; and (2) how to measure, which asks how to devise II. RELATED WORK new methods to measure security metrics. In this work, we are interested in answering the latter question, how to measure a In practice, obtaining ground truth is highly challenging and security metric where the ground truth does not exist for the almost not feasible due to high noise, uncertain data, and/or detection accuracy of a malware detector as well as for the the inherent nature of imperfect estimation. For example, class (i.e., malicious or benign) of the files. when using machine learning techniques to train cyber defense When measuring the quality of malware detectors, many models, we need to know the ground truth labels of training methods have been used based on certain heuristics such samples. For a small set of samples, we can use human experts as using the labels of a few malware detectors as ground to grade them and derive their ground truth. However, even truth [1, 2, 3]. These heuristic-based approaches are trou- in this case, the perfect evaluation is not guaranteed because blesome because of the well-known fact that each malware humans are also error-prone and can make mistakes due to detector has a different quality of detection accuracy. Although their inherent cognitive limitations. Accordingly, for a large some methods have been proposed to answer how to measure set of samples, it is obviously not feasible for human experts security metrics [4, 5], measuring the relative accuracy of to derive the ground truth. Therefore, it is true that many third- malware detectors has not been addressed in existing works. party datasets (e.g., blacklisted websites [6, 7, 8, 9]) are not In particular, this work is inspired by our prior work [4] necessarily trustworthy due to these inherent limitations. which measured the quality of malware detectors assuming Several studies have been conducted in order to investigate that a voting-based estimation of detection accuracy is true. the accuracy of malware detectors when there exists no ground Unlike [4], this work aims to estimate the relative accuracy truth of their accuracy [4, 5, 10, 11]. These studies used of malware detectors, which are obtained without making the different assumptions in order to estimate the accuracy of the malware detectors. Kantchelian et al. [5] used the na¨ıve This work is done when Jin-Hee Cho was with US Army Research Bayesian method and treated the unknown ground truth labels Laboratory. as hidden variables, while the Expectation-Maximization (EM) 978-1-5386-7185-6/18/$31.00 ©2018 IEEE 450 Milcom 2018 Track 3 - Cyber Security and Trusted Computing method [10, 11] is used to estimate the accuracy of malware more interested in knowing which detector is more accurate detectors using well-known metrics such as false-positive rate, than others, leading to generating the ranks of examined false-negative rate, or accuracy. In [5], the authors assumed the detectors. Based on our proposed methodology, we obtain homogeneity of false positives in all detectors, an independent their respective relative accuracy as T1 = 100%, T2 = 90%, and decision of each detector, and low false positives but high false T3 = 70%, which gives the performance of relative accuracy of negatives assumed for all detectors, and so forth. However, the detectors: D1 > D2 > D3. However, the relative accuracy these assumptions should be removed in order to reflect real does not approximate the true accuracy. Moreover, when we world applications. Xu et al. [4] used a frequentist approach consider a set of files scanned by detectors, D1, D2, D3, to design a statistical metric estimator to measure the quality and D4, letting the true accuracy of D1-D3 remain the same metrics of malware detectors with only two of the four as- while the true accuracy of D4 is 95%, then the resulting sumptions made in [5]. All the above works [4, 5, 10, 11] make relative accuracy may be T1 = 80%, T2 = 60%, T3 = 50%, and certain assumptions. In contrast, the present paper investigates T4 = 100%. This leads to the relative accuracy of the detectors the relative accuracy of malware detectors without making being D4 > D1 > D2 > D3. This is because the detector with those assumptions. the highest relative accuracy is always normalized to have a The paper falls into the study of security metrics, which is relative accuracy of 100% and the relative accuracy is always an integral part of the Cybersecurity Dynamics framework [12, measured over a set of detectors. 13] and indeed one of the most fundamental open problems B. Methodology that have yet to be adequately tackled [14]. Recent advance- The basic underlying idea of estimating the relative accuracy ment in security metrics includes [14, 15, 16, 17, 18, 19]. For of malware detectors is to measure the similarity between each example, the effectiveness of firewalls and DMZs is studied in pair of detectors. To do so, we iteratively create the relative [18] and the effectiveness of enforcing network-wide software accuracy of the malware detectors, given that the initial relative diversity is investigated in [17]. Orthogonal to security metrics accuracy of each detector is set to 1, assuming that each research are the first-principle modeling of cybersecurity from detector is equally accurate. a holistic perspective [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30] 1) Similarity Matrix: To measure the relative accuracy of and cybersecurity data analytics [31, 32, 33, 34, 35]. detectors, the concept of a similarity matrix is introduced to III. PROBLEM STATEMENT AND METHODOLOGY collectively represent the similarity between malware detectors according to their decisions in labeling files as benign or A. Definitions of Relative Accuracy of Malware Detectors malicious. In this matrix, denoted by S = (Sik), the i-th row Suppose that there are m files, denoted by F1;:::;Fj;:::;Fm corresponds to detector Di and the k-th column corresponds and n malware detectors, denoted by D1;:::;Di;:::;Dn. The to detector Dk, where 1 ≤ i;k ≤ n. Element Sik denotes the input dataset is represented by a matrix V = (Vi j)1≤i≤n;1≤ j≤m, similarity between detectors Di and Dk in terms of their which is defined where capabilities in detecting malware. Naturally, we require (i) 8 Sik = Ski because the similarity should be symmetric; and (ii) >1 if Di detects Fj as malicious, < Sii = 1 for any 1 ≤ i ≤ n. Intuitively, the similarity between Di Vi j = 0 if Di detects Fj as benign, and Dk, Sik, is defined by the ratio of the number of decisions :> −1 if Di did not scan Fj. where Di and Dk agree with each other over the total number of files scanned by both detectors, D and D . Vector V = (V ;:::;V ;:::;V ), where 1 ≤ i ≤ n, represents i k i i1 i j im To clearly define S in a modular fashion, two auxiliary the outcome of using detector D to label m files. ik i matrices are defined: the agreement matrix, denoted by A = With respect to a set of n detectors, the relative accuracy of (A ) , and the count matrix, denoted by C = (C ) .
Load more

Recommended publications
  • Testing Anti-Virus in Linux: How Effective Are the Solutions Available for Desktop Computers?
    Royal Holloway University of London ISG MSc Information Security thesis series 2021 Testing anti-virus in Linux: How effective are the solutions available for desktop computers? Authors Giuseppe Raffa, MSc (Royal Holloway, 2020) Daniele Sgandurra, Huawei, Munich Research Center. (Formerly ISG, Royal Holloway.) Abstract Anti-virus (AV) programs are widely recognized as one of the most important defensive tools available for desktop computers. Regardless of this, several Linux users consider AVs unnec- essary, arguing that this operating system (OS) is “malware-free”. While Windows platforms are undoubtedly more affected by malicious software, there exist documented cases of Linux- specific malware. In addition, even though the estimated market share of Linux desktop sys- tems is currently only at 2%, it is certainly possible that it will increase in the near future. Considering all this, and the lack of up-to-date information about Linux-compatible AV solutions, we evaluated the effectiveness of some anti-virus products by using local installations, a well- known on-line malware scanning service (VirusTotal) and a renowned penetration testing tool (Metasploit). Interestingly, in our tests, the average detection rate of the locally-installed AV programs was always above 80%. However, when we extended our analysis to the wider set of anti-virus solutions available on VirusTotal, we found out that the average detection rate barely reached 60%. Finally, when evaluating malicious files created with Metasploit, we verified that the AVs’ heuristic detection mechanisms performed very poorly, with detection rates as low as 8.3%.a aThis article is published online by Computer Weekly as part of the 2021 Royal Holloway informa- tion security thesis series https://www.computerweekly.com/ehandbook/Royal-Holloway-Testing-antivirus- efficacy-in-Linux.
    [Show full text]
  • Hostscan 4.8.01064 Antimalware and Firewall Support Charts
    HostScan 4.8.01064 Antimalware and Firewall Support Charts 10/1/19 © 2019 Cisco and/or its affiliates. All rights reserved. This document is Cisco public. Page 1 of 76 Contents HostScan Version 4.8.01064 Antimalware and Firewall Support Charts ............................................................................... 3 Antimalware and Firewall Attributes Supported by HostScan .................................................................................................. 3 OPSWAT Version Information ................................................................................................................................................. 5 Cisco AnyConnect HostScan Antimalware Compliance Module v4.3.890.0 for Windows .................................................. 5 Cisco AnyConnect HostScan Firewall Compliance Module v4.3.890.0 for Windows ........................................................ 44 Cisco AnyConnect HostScan Antimalware Compliance Module v4.3.824.0 for macos .................................................... 65 Cisco AnyConnect HostScan Firewall Compliance Module v4.3.824.0 for macOS ........................................................... 71 Cisco AnyConnect HostScan Antimalware Compliance Module v4.3.730.0 for Linux ...................................................... 73 Cisco AnyConnect HostScan Firewall Compliance Module v4.3.730.0 for Linux .............................................................. 76 ©201 9 Cisco and/or its affiliates. All rights reserved. This document is Cisco Public.
    [Show full text]
  • Page 1 of 3 Virustotal
    VirusTotal - Free Online Virus, Malware and URL Scanner Page 1 of 3 VT Community Sign in ▼ Languages ▼ Virustotal is a service that analyzes suspicious files and URLs and facilitates the quick detection of viruses, worms, trojans, and all kinds of malware detected by antivirus engines. More information... 0 VT Community user(s) with a total of 0 reputation credit(s) say(s) this sample is goodware. 0 VT Community VT Community user(s) with a total of 0 reputation credit(s) say(s) this sample is malware. File name: wsusoffline71.zip Submission date: 2011-11-01 08:16:44 (UTC) Current status: finished not reviewed Result: 0 /40 (0.0%) Safety score: - Compact Print results Antivirus Version Last Update Result AhnLab-V3 2011.10.31.00 2011.10.31 - AntiVir 7.11.16.225 2011.10.31 - Antiy-AVL 2.0.3.7 2011.11.01 - Avast 6.0.1289.0 2011.11.01 - AVG 10.0.0.1190 2011.11.01 - BitDefender 7.2 2011.11.01 - CAT-QuickHeal 11.00 2011.11.01 - ClamAV 0.97.3.0 2011.11.01 - Commtouch 5.3.2.6 2011.11.01 - Comodo 10625 2011.11.01 - Emsisoft 5.1.0.11 2011.11.01 - eSafe 7.0.17.0 2011.10.30 - eTrust-Vet 36.1.8650 2011.11.01 - F-Prot 4.6.5.141 2011.11.01 - F-Secure 9.0.16440.0 2011.11.01 - Fortinet 4.3.370.0 2011.11.01 - GData 22 2011.11.01 - Ikarus T3.1.1.107.0 2011.11.01 - Jiangmin 13.0.900 2011.10.31 - K7AntiVirus 9.116.5364 2011.10.31 - Kaspersky 9.0.0.837 2011.11.01 - McAfee 5.400.0.1158 2011.11.01 - McAfee-GW-Edition 2010.1D 2011.10.31 - Microsoft 1.7801 2011.11.01 - NOD32 6591 2011.11.01 - Norman 6.07.13 2011.10.31 - nProtect 2011-10-31.01 2011.10.31 - http://www.virustotal.com/file -scan/report.html?id=874d6968eaf6eeade19179712d53 ..
    [Show full text]
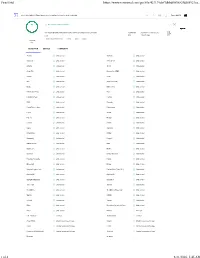
  • Virustotal Scan on 2020.08.21 for Pbidesktopsetup 2
    VirusTotal https://www.virustotal.com/gui/file/423139def3dbbdf0f5682fdd88921ea... 423139def3dbbdf0f5682fdd88921eaface84ff48ef2e2a8d20e4341ca4a4364 Patch My PC No engines detected this file 423139def3dbbdf0f5682fdd88921eaface84ff48ef2e2a8d20e4341ca4a4364 269.49 MB 2020-08-21 11:39:09 UTC setup Size 1 minute ago invalid-rich-pe-linker-version overlay peexe signed Community Score DETECTION DETAILS COMMUNITY Acronis Undetected Ad-Aware Undetected AegisLab Undetected AhnLab-V3 Undetected Alibaba Undetected ALYac Undetected Antiy-AVL Undetected SecureAge APEX Undetected Arcabit Undetected Avast Undetected AVG Undetected Avira (no cloud) Undetected Baidu Undetected BitDefender Undetected BitDefenderTheta Undetected Bkav Undetected CAT-QuickHeal Undetected ClamAV Undetected CMC Undetected Comodo Undetected CrowdStrike Falcon Undetected Cybereason Undetected Cyren Undetected eScan Undetected F-Secure Undetected FireEye Undetected Fortinet Undetected GData Undetected Ikarus Undetected Jiangmin Undetected K7AntiVirus Undetected K7GW Undetected Kaspersky Undetected Kingsoft Undetected Malwarebytes Undetected MAX Undetected MaxSecure Undetected McAfee Undetected Microsoft Undetected NANO-Antivirus Undetected Palo Alto Networks Undetected Panda Undetected Qihoo-360 Undetected Rising Undetected Sangfor Engine Zero Undetected SentinelOne (Static ML) Undetected Sophos AV Undetected Sophos ML Undetected SUPERAntiSpyware Undetected Symantec Undetected TACHYON Undetected Tencent Undetected TrendMicro Undetected TrendMicro-HouseCall Undetected VBA32 Undetected
    [Show full text]
  • An Analysis of Domain Classification Services
    Mis-shapes, Mistakes, Misfits: An Analysis of Domain Classification Services Pelayo Vallina Victor Le Pochat Álvaro Feal IMDEA Networks Institute / imec-DistriNet, KU Leuven IMDEA Networks Institute / Universidad Carlos III de Madrid Universidad Carlos III de Madrid Marius Paraschiv Julien Gamba Tim Burke IMDEA Networks Institute IMDEA Networks Institute / imec-DistriNet, KU Leuven Universidad Carlos III de Madrid Oliver Hohlfeld Juan Tapiador Narseo Vallina-Rodriguez Brandenburg University of Universidad Carlos III de Madrid IMDEA Networks Institute/ICSI Technology ABSTRACT ACM Reference Format: Domain classification services have applications in multiple areas, Pelayo Vallina, Victor Le Pochat, Álvaro Feal, Marius Paraschiv, Julien including cybersecurity, content blocking, and targeted advertising. Gamba, Tim Burke, Oliver Hohlfeld, Juan Tapiador, and Narseo Vallina- Rodriguez. 2020. Mis-shapes, Mistakes, Misfits: An Analysis of Domain Yet, these services are often a black box in terms of their method- Classification Services. In ACM Internet Measurement Conference (IMC ’20), ology to classifying domains, which makes it difficult to assess October 27ś29, 2020, Virtual Event, USA. ACM, New York, NY, USA, 21 pages. their strengths, aptness for specific applications, and limitations. In https://doi.org/10.1145/3419394.3423660 this work, we perform a large-scale analysis of 13 popular domain classification services on more than 4.4M hostnames. Our study empirically explores their methodologies, scalability limitations, 1 INTRODUCTION label constellations, and their suitability to academic research as The need to classify websites became apparent in the early days well as other practical applications such as content filtering. We of the Web. The first generation of domain classification services find that the coverage varies enormously across providers, ranging appeared in the late 1990s in the form of web directories.
    [Show full text]
  • Security Survey 2014
    Security Survey 2014 www.av-comparatives.org IT Security Survey 2014 Language: English Last Revision: 28th February 2014 www.av-comparatives.org - 1 - Security Survey 2014 www.av-comparatives.org Overview Use of the Internet by home and business users continues to grow in all parts of the world. How users access the Internet is changing, though. There has been increased usage of smartphones by users to access the Internet. The tablet market has taken off as well. This has resulted in a drop in desktop and laptop sales. With respect to attacks by cyber criminals, this means that their focus has evolved. This is our fourth1 annual survey of computer users worldwide. Its focus is which security products (free and paid) are employed by users, OS usage, and browser usage. We also asked respondents to rank what they are looking for in their security solution. Survey methodology Report results are based on an Internet survey run by AV-Comparatives between 17th December 2013 and 17th January 2014. A total of 5,845 computer users from around the world anonymously answered the questions on the subject of computers and security. Key Results Among respondents, the three most important aspects of a security protection product were (1) Low impact on system performance (2) Good detection rate (3) Good malware removal and cleaning capabilities. These were the only criteria with over 60% response rate. Europe, North America and Central/South America were similar in terms of which products they used, with Avast topping the list. The share of Android as the mobile OS increased from 51% to 70%, while Symbian dropped from 21% to 5%.
    [Show full text]
  • Page 1 of 375 6/16/2021 File:///C:/Users/Rtroche
    Page 1 of 375 :: Access Flex Bear High Yield ProFund :: Schedule of Portfolio Investments :: April 30, 2021 (unaudited) Repurchase Agreements(a) (27.5%) Principal Amount Value Repurchase Agreements with various counterparties, 0.00%, dated 4/30/21, due 5/3/21, total to be received $129,000. $ 129,000 $ 129,000 TOTAL REPURCHASE AGREEMENTS (Cost $129,000) 129,000 TOTAL INVESTMENT SECURITIES 129,000 (Cost $129,000) - 27.5% Net other assets (liabilities) - 72.5% 340,579 NET ASSETS - (100.0%) $ 469,579 (a) The ProFund invests in Repurchase Agreements jointly with other funds in the Trust. See "Repurchase Agreements" in the Appendix to view the details of each individual agreement and counterparty as well as a description of the securities subject to repurchase. Futures Contracts Sold Number Value and Unrealized of Expiration Appreciation/ Contracts Date Notional Amount (Depreciation) 5-Year U.S. Treasury Note Futures Contracts 3 7/1/21 $ (371,977) $ 2,973 Centrally Cleared Swap Agreements Credit Default Swap Agreements - Buy Protection (1) Implied Credit Spread at Notional Premiums Unrealized Underlying Payment Fixed Deal Maturity April 30, Amount Paid Appreciation/ Variation Instrument Frequency Pay Rate Date 2021(2) (3) Value (Received) (Depreciation) Margin CDX North America High Yield Index Swap Agreement; Series 36 Daily 5 .00% 6/20/26 2.89% $ 450,000 $ (44,254) $ (38,009) $ (6,245) $ 689 (1) When a credit event occurs as defined under the terms of the swap agreement, the Fund as a buyer of credit protection will either (i) receive from the seller of protection an amount equal to the par value of the defaulted reference entity and deliver the reference entity or (ii) receive a net amount equal to the par value of the defaulted reference entity less its recovery value.
    [Show full text]
  • Aluria Security Center Avira Antivir Personaledition Classic 7
    Aluria Security Center Avira AntiVir PersonalEdition Classic 7 - 8 Avira AntiVir Personal Free Antivirus ArcaVir Antivir/Internet Security 09.03.3201.9 x64 Ashampoo FireWall Ashampoo FireWall PRO 1.14 ALWIL Software Avast 4.0 Grisoft AVG 7.x Grisoft AVG 6.x Grisoft AVG 8.x Grisoft AVG 8.x x64 Avira Premium Security Suite 2006 Avira WebProtector 2.02 Avira AntiVir Personal - Free Antivirus 8.02 Avira AntiVir PersonalEdition Premium 7.06 AntiVir Windows Workstation 7.06.00.507 Kaspersky AntiViral Toolkit Pro BitDefender Free Edition BitDefender Internet Security BullGuard BullGuard AntiVirus BullGuard AntiVirus x64 CA eTrust AntiVirus 7 CA eTrust AntiVirus 7.1.0192 eTrust AntiVirus 7.1.194 CA eTrust AntiVirus 7.1 CA eTrust Suite Personal 2008 CA Licensing 1.57.1 CA Personal Firewall 9.1.0.26 CA Personal Firewall 2008 CA eTrust InoculateIT 6.0 ClamWin Antivirus ClamWin Antivirus x64 Comodo AntiSpam 2.6 Comodo AntiSpam 2.6 x64 COMODO AntiVirus 1.1 Comodo BOClean 4.25 COMODO Firewall Pro 1.0 - 3.x Comodo Internet Security 3.8.64739.471 Comodo Internet Security 3.8.64739.471 x64 Comodo Safe Surf 1.0.0.7 Comodo Safe Surf 1.0.0.7 x64 DrVirus 3.0 DrWeb for Windows 4.30 DrWeb Antivirus for Windows 4.30 Dr.Web AntiVirus 5 Dr.Web AntiVirus 5.0.0 EarthLink Protection Center PeoplePC Internet Security 1.5 PeoplePC Internet Security Pack / EarthLink Protection Center ESET NOD32 file on-access scanner ESET Smart Security 3.0 eTrust EZ Firewall 6.1.7.0 eTrust Personal Firewall 5.5.114 CA eTrust PestPatrol Anti-Spyware Corporate Edition CA eTrust PestPatrol
    [Show full text]
  • Ten Strategies of a World-Class Cybersecurity Operations Center Conveys MITRE’S Expertise on Accumulated Expertise on Enterprise-Grade Computer Network Defense
    Bleed rule--remove from file Bleed rule--remove from file MITRE’s accumulated Ten Strategies of a World-Class Cybersecurity Operations Center conveys MITRE’s expertise on accumulated expertise on enterprise-grade computer network defense. It covers ten key qualities enterprise- grade of leading Cybersecurity Operations Centers (CSOCs), ranging from their structure and organization, computer MITRE network to processes that best enable effective and efficient operations, to approaches that extract maximum defense Ten Strategies of a World-Class value from CSOC technology investments. This book offers perspective and context for key decision Cybersecurity Operations Center points in structuring a CSOC and shows how to: • Find the right size and structure for the CSOC team Cybersecurity Operations Center a World-Class of Strategies Ten The MITRE Corporation is • Achieve effective placement within a larger organization that a not-for-profit organization enables CSOC operations that operates federally funded • Attract, retain, and grow the right staff and skills research and development • Prepare the CSOC team, technologies, and processes for agile, centers (FFRDCs). FFRDCs threat-based response are unique organizations that • Architect for large-scale data collection and analysis with a assist the U.S. government with limited budget scientific research and analysis, • Prioritize sensor placement and data feed choices across development and acquisition, enteprise systems, enclaves, networks, and perimeters and systems engineering and integration. We’re proud to have If you manage, work in, or are standing up a CSOC, this book is for you. served the public interest for It is also available on MITRE’s website, www.mitre.org. more than 50 years.
    [Show full text]
  • Measuring and Modeling the Label Dynamics of Online Anti-Malware Engines
    Measuring and Modeling the Label Dynamics of Online Anti-Malware Engines Shuofei Zhu1, Jianjun Shi1,2, Limin Yang3 Boqin Qin1,4, Ziyi Zhang1,5, Linhai Song1, Gang Wang3 1The Pennsylvania State University 2Beijing Institute of Technology 3University of Illinois at Urbana-Champaign 4Beijing University of Posts and Telecommunications 5University of Science and Technology of China 1 VirusTotal • The largest online anti-malware scanning service – Applies 70+ anti-malware engines – Provides analysis reports and rich metadata • Widely used by researchers in the security community report API scan API Metadata Submitter Sample Reports 2 Challenges of Using VirusTotal • Q1: When VirusTotal labels are trustworthy? McAfee ✔️ ⚠️ ⚠️ ✔️ ✔️ Day 1 2 3 4 5 6 Time Sample 3 Challenges of Using VirusTotal • Q1: When VirusTotal labels are trustworthy? • Q2: How to aggregate labels from different engines? • Q3: Are different engines equally trustworthy? Engines Results McAfee ⚠️ ⚠️ Microsoft ✔️ ✔️ Kaspersky ✔️ Avast ⚠️ … 3 Challenges of Using VirusTotal • Q1: When VirusTotal labels are trustworthy? • Q2: How to aggregate labels from different engines? • Q3: Are different engines equally trustworthy? Equally trustworthy? 3 Literature Survey on VirusTotal Usages • Surveyed 115 top-tier conference papers that use VirusTotal • Our findings: – Q1: rarely consider label changes – Q2: commonly use threshold-based aggregation methods – Q3: often treat different VirusTotal engines equally Consider Label Changes Threshold-Based Method Reputable Engines Yes Yes No Yes
    [Show full text]
  • Heuristic / Behavioural Protection Test 2013
    Anti‐Virus Comparative ‐ Retrospective test – March 2013 www.av‐comparatives.org Anti-Virus Comparative Retrospective/Proactive test Heuristic and behavioural protection against new/unknown malicious software Language: English March 2013 Last revision: 16th August 2013 www.av-comparatives.org ‐ 1 ‐ Anti‐Virus Comparative ‐ Retrospective test – March 2013 www.av‐comparatives.org Contents 1. Introduction 3 2. Description 3 3. False-alarm test 5 4. Test Results 5 5. Summary results 6 6. Awards reached in this test 7 7. Copyright and disclaimer 8 ‐ 2 ‐ Anti‐Virus Comparative ‐ Retrospective test – March 2013 www.av‐comparatives.org 1. Introduction This test report is the second part of the March 2013 test1. The report is delivered several months later due to the large amount of work required, deeper analysis, preparation and dynamic execution of the retrospective test-set. This type of test is performed only once a year and includes a behavioural protection element, where any malware samples are executed, and the results observed. Although it is a lot of work, we usually receive good feedback from various vendors, as this type of test allows them to find bugs and areas for improvement in the behavioural routines (as this test evaluates specifically the proactive heuristic and behavioural protection components). The products used the same updates and signatures that they had on the 28th February 2013. This test shows the proactive protection capabilities that the products had at that time. We used 1,109 new, unique and very prevalent malware samples that appeared for the first time shortly after the freezing date. The size of the test-set has also been reduced to a smaller set containing only one unique sam- ple per variant, in order to enable vendors to peer-review our results in a timely manner.
    [Show full text]
  • ESET THREAT REPORT Q3 2020 | 2 ESET Researchers Reveal That Bugs Similar to Krøøk Affect More Chip Brands Than Previously Thought
    THREAT REPORT Q3 2020 WeLiveSecurity.com @ESETresearch ESET GitHub Contents Foreword Welcome to the Q3 2020 issue of the ESET Threat Report! 3 FEATURED STORY As the world braces for a pandemic-ridden winter, COVID-19 appears to be losing steam at least in the cybercrime arena. With coronavirus-related lures played out, crooks seem to 5 NEWS FROM THE LAB have gone “back to basics” in Q3 2020. An area where the effects of the pandemic persist, however, is remote work with its many security challenges. 9 APT GROUP ACTIVITY This is especially true for attacks targeting Remote Desktop Protocol (RDP), which grew throughout all H1. In Q3, RDP attack attempts climbed by a further 37% in terms of unique 13 STATISTICS & TRENDS clients targeted — likely a result of the growing number of poorly secured systems connected to the internet during the pandemic, and possibly other criminals taking inspiration from 14 Top 10 malware detections ransomware gangs in targeting RDP. 15 Downloaders The ransomware scene, closely tracked by ESET specialists, saw a first this quarter — an attack investigated as a homicide after the death of a patient at a ransomware-struck 17 Banking malware hospital. Another surprising twist was the revival of cryptominers, which had been declining for seven consecutive quarters. There was a lot more happening in Q3: Emotet returning 18 Ransomware to the scene, Android banking malware surging, new waves of emails impersonating major delivery and logistics companies…. 20 Cryptominers This quarter’s research findings were equally as rich, with ESET researchers: uncovering 21 Spyware & backdoors more Wi-Fi chips vulnerable to KrØØk-like bugs, exposing Mac malware bundled with a cryptocurrency trading application, discovering CDRThief targeting Linux VoIP softswitches, 22 Exploits and delving into KryptoCibule, a triple threat in regard to cryptocurrencies.
    [Show full text]