Energy-Efficient ARM64 Cluster with Cryptanalytic Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HTC Desire 826 Dual Sim 2 Contents Contents
User guide HTC Desire 826 dual sim 2 Contents Contents What's new Android 6.0 Marshmallow 9 Software and app updates 10 Unboxing HTC Desire 826 11 nano UIM and nano SIM cards 12 Storage card 14 Battery 16 Switching the power on or off 16 Managing your nano UIM and nano SIM cards with Dual network manager 17 Phone setup and transfer Setting up HTC Desire 826 for the first time 18 Restoring content from HTC Backup 19 Transferring content from an Android phone 19 Ways of transferring content from an iPhone 20 Transferring iPhone content through iCloud 20 Transferring contacts from your old phone through Bluetooth 20 Other ways of getting contacts and other content 21 Transferring photos, videos, and music between your phone and computer 22 Using Quick Settings 22 Getting to know your settings 24 Updating your phone's software 24 Getting apps from Google Play 26 Downloading apps from the web 27 Uninstalling an app 28 Your first week with your new phone Basics 29 HTC Sense Home widget 37 Lock screen 39 Notifications 42 Working with text 43 HTC Help 47 Phone calls Making a call with Smart dial 48 3 Contents Making a call with your voice 48 Dialing an extension number 49 Returning a missed call 49 Speed dial 49 Calling a number in a message, email, or calendar event 49 Making an emergency call 50 Receiving calls 50 What can I do during a call? 50 Setting up a conference call (GSM) 51 Call History 52 Switching between silent, vibrate, and normal modes 52 Home dialing 53 Messages Sending a text message (SMS) 54 Sending a multimedia message (MMS) -

Factory Model Device Model
Factory Model Device Model Acer A1-713 acer_aprilia Acer A1-811 mango Acer A1-830 ducati Acer A3-A10 G1EA3 Acer A3-A10 mtk6589_e_lca Acer A3-A10 zara Acer A3-A20 acer_harley Acer A3-A20FHD acer_harleyfhd Acer Acer E320-orange C6 Acer Aspire A3 V7 Acer AT390 T2 Acer B1-723 oban Acer B1-730 EverFancy D40 Acer B1-730 vespatn Acer CloudMobile S500 a9 Acer DA220HQL lenovo72_we_jb3 Acer DA222HQL N451 Acer DA222HQLA A66 Acer DA222HQLA Flare S3 Power Acer DA226HQ tianyu72_w_hz_kk Acer E330 C7 Acer E330 GT-N7105T Acer E330 STUDIO XL Acer E350 C8n Acer E350 wiko Acer G100W maya Acer G1-715 A510s Acer G1-715 e1808_v75_hjy1_5640_maxwest Acer Icona One 7 vespa Acer Iconia One 7 AT1G* Acer Iconia One 7 G1-725 Acer Iconia One 7 m72_emmc_s6_pcb22_1024_8g1g_fuyin Acer Iconia One 7 vespa2 Acer Iconia One 8 vespa8 Acer Iconia Tab 7 acer_apriliahd Acer Iconia Tab 8 ducati2fhd Acer Iconia Tab 8 ducati2hd Acer Iconia Tab 8 ducati2hd3g Acer Iconia Tab 8 Modelo II - Professor Acer Iconia Tab A100 (VanGogh) vangogh Acer Iconia Tab A200 s7503 Acer Iconia Tab A200 SM-N9006 Acer Iconia Tab A501 ELUGA_Mark Acer Iconia Tab A501 picasso Acer Iconia Tab A510 myPhone Acer Iconia Tab A510 picasso_m Acer Iconia Tab A510 ZUUM_M50 Acer Iconia Tab A701 picasso_mf Acer Iconia Tab A701 Revo_HD2 Acer Iconia TalkTab 7 acer_a1_724 Acer Iconia TalkTab 7 AG CHROME ULTRA Acer Liquid a1 Acer Liquid C1 I1 Acer Liquid C1 l3365 Acer Liquid E1 C10 Acer Liquid E2 C11 Acer Liquid E3 acer_e3 Acer Liquid E3 acer_e3n Acer Liquid E3 LS900 Acer Liquid E3 Quasar Acer Liquid E600 e600 Acer Liquid -
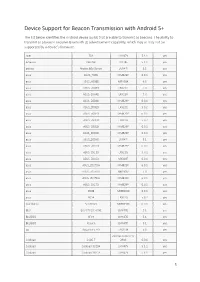
Device Support for Beacon Transmission with Android 5+
Device Support for Beacon Transmission with Android 5+ The list below identifies the Android device builds that are able to transmit as beacons. The ability to transmit as a beacon requires Bluetooth LE advertisement capability, which may or may not be supported by a device’s firmware. Acer T01 LMY47V 5.1.1 yes Amazon KFFOWI LVY48F 5.1.1 yes archos Archos 80d Xenon LMY47I 5.1 yes asus ASUS_T00N MMB29P 6.0.1 yes asus ASUS_X008D MRA58K 6.0 yes asus ASUS_Z008D LRX21V 5.0 yes asus ASUS_Z00AD LRX21V 5.0 yes asus ASUS_Z00AD MMB29P 6.0.1 yes asus ASUS_Z00ED LRX22G 5.0.2 yes asus ASUS_Z00ED MMB29P 6.0.1 yes asus ASUS_Z00LD LRX22G 5.0.2 yes asus ASUS_Z00LD MMB29P 6.0.1 yes asus ASUS_Z00UD MMB29P 6.0.1 yes asus ASUS_Z00VD LMY47I 5.1 yes asus ASUS_Z010D MMB29P 6.0.1 yes asus ASUS_Z011D LRX22G 5.0.2 yes asus ASUS_Z016D MXB48T 6.0.1 yes asus ASUS_Z017DA MMB29P 6.0.1 yes asus ASUS_Z017DA NRD90M 7.0 yes asus ASUS_Z017DB MMB29P 6.0.1 yes asus ASUS_Z017D MMB29P 6.0.1 yes asus P008 MMB29M 6.0.1 yes asus P024 LRX22G 5.0.2 yes blackberry STV100-3 MMB29M 6.0.1 yes BLU BLU STUDIO ONE LMY47D 5.1 yes BLUBOO XFire LMY47D 5.1 yes BLUBOO Xtouch LMY47D 5.1 yes bq Aquaris E5 HD LRX21M 5.0 yes ZBXCNCU5801712 Coolpad C106-7 291S 6.0.1 yes Coolpad Coolpad 3320A LMY47V 5.1.1 yes Coolpad Coolpad 3622A LMY47V 5.1.1 yes 1 CQ CQ-BOX 2.1.0-d158f31 5.1.1 yes CQ CQ-BOX 2.1.0-f9c6a47 5.1.1 yes DANY TECHNOLOGIES HK LTD Genius Talk T460 LMY47I 5.1 yes DOOGEE F5 LMY47D 5.1 yes DOOGEE X5 LMY47I 5.1 yes DOOGEE X5max MRA58K 6.0 yes elephone Elephone P7000 LRX21M 5.0 yes Elephone P8000 -

新到货~ 14天机(定稿) 看货时间 ︰11Am 截标时间 : 4Pm 交货时间: 5Pm 投标前请仔细阅读本司关于各级别及相关退货定义 参与投标者则代表已阅读及同意该规则及退货定义 清单摘要: 任何数量, 均可以出价! 一
光义有限公司 投标清单 表格编号: F-007-02 投标日期: 2021-10-06 供货商及等级: 新到货~ 14天机(定稿) 看货时间 ︰11am 截标时间 : 4pm 交货时间: 5pm 投标前请仔细阅读本司关于各级别及相关退货定义 参与投标者则代表已阅读及同意该规则及退货定义 清单摘要: 任何数量, 均可以出价! 一. 周三竞标日(2021-10-06)14天机竞标总数 188641台(苹果手机10395台、三星高档手机 8427台)。 二. 其中, 苹果I-phone 12// 11系列1215台、I-phone XS/XS Max系列184台、iPhone X/XR系列61台、iPhone 8/8 Plus 系列199台、iPhone 7/7Plus系列2769台、iPhone 6s/6s Plus系列1089台、iPhone 6/6 Plus系列1728台、I-pad系列776 台 、 。 三星G988/G986 0台、N960F/N970F/N976F 7台、G970/G973/G975/G977 35台、F700/F900 0台。 三. 以下是重要型号分布 品牌 型号 数量 级别 Lot 7 Mobiphone 3G 合计 1000 汇总 美国V版原箱单投 美国V版原箱单投 合计 379 汇总 Apple I-Phone 12 Pro Max 合计 46 汇总 Apple I-Phone 12 Pro 合计 32 汇总 Apple I-Phone 12 合计 89 汇总 Apple I-Phone 12 Mini 合计 40 汇总 Apple I-Phone 11 Pro Max 合计 59 汇总 Apple I-Phone 11 Pro 合计 85 汇总 Apple I-Phone 11 合计 438 汇总 Apple I-Phone XS Max 合计 149 汇总 Apple I-Phone XS 合计 14 汇总 Apple I-Phone XR 合计 39 汇总 Apple I-Phone X 合计 11 汇总 Apple I-Phone 8 Plus 合计 49 汇总 Apple I-Phone 8 合计 95 汇总 Apple I-Phone 7 Plus 合计 196 汇总 Apple I-Phone 7 合计 2496 汇总 Apple I-Phone 6S Plus 合计 120 汇总 Apple I-Phone 6S 合计 906 汇总 Apple I-Phone 6 Plus 合计 331 汇总 Apple I-Phone 6 合计 1280 汇总 Apple I-Phone 5S 合计 435 汇总 Apple I-Phone 5C 合计 315 汇总 Apple I-Phone SE2 合计 71 汇总 Apple I-Phone SE 合计 93 汇总 Apple I-Phone 5 合计 73 汇总 Apple I-Phone 4S 合计 277 汇总 Apple I-Phone 4 合计 256 汇总 Apple 云 合计 834 汇总 Apple I-Pad 合计 242 汇总 四. -
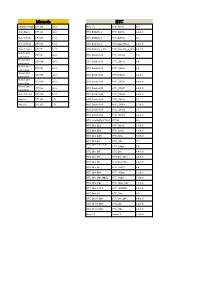
Motorola HTC DROIDTURBO XT1254 4.4.3 HTC 10 HTC M10h 6.0
Motorola HTC DROIDTURBO XT1254 4.4.3 HTC 10 HTC_M10h 6.0 Moto Maxx XT1225 4.4.3 HTC Butterfly 2 HTC_B810x 4.4-6.0 Moto X Play XT1563 5.1.1 HTC Butterfly 3 HTC_B830x 6.0 Moto X Play XT1562 5.1.1 HTC Butterfly s HTC_Butterfly_s 4.4-5.0 Moto X Style XT1572 5.1.1 HTC Butterfly s 4G HTC_Butterfly_s_901s 4.4-5.0 MotoX 2nd XT1097 4.4.3 HTC Desire 530 HTC_D530x 6.0 generation MotoX 2nd XT1094 4.4.3 HTC Desire 610 HTC_D610x 4.4 generation MotoX 2nd XT1093 4.4.3 HTC Desire 620 HTC_D620x 4.4 generation MotoX 2nd XT1095 4.4.3 HTC Desire 626 HTC_D626x 4.4-5.1 generation MotoX 2nd XT1096 4.4.3 HTC Desire 816 HTC_D816x 4.4-6.0 generation MotoX 2nd XT1092 4.4.3 HTC Desire 820 HTC_D820f 4.4-6.0 generation Moto X Force XT1580 5.1.1 HTC Desire 820 HTC_D820u 4.4-6.0 Nexus 6 XT1103 5.0 HTC Desire 825 HTC_D825x 6.0 Nexus 6 XT1100 5.0 HTC Desire 826 HTC_D826x 5.0-6.0 HTC Desire 830 HTC_D830x 5.1 HTC Desire Eye HTC_M910x 4.4-6.0 HTC J butterfly HTV31 HTV31 6.0 HTC One (E8) HTC_M8Sx 4.4-6.0 HTC One (E8) HTC_M8Sy 4.4-6.0 HTC One (M9) HTC_M9u 5.0-6.0 HTC One A9 HTC_A9u 6.0 HTC One E9+ Dual HTC_E9pw 5.0 SIM HTC One M7 HTC One 4.4-5.0 HTC One M7 HTC One 801e 4.4-5.0 HTC One M7 HTC One 801s 4.4-5.0 HTC One M7 HTC_PN071 4.4 HTC One M9+ HTC_M9pw 5.0-6.0 HTC One M9+ (極光) HTC_M9px 5.0-6.0 HTC One max HTC_One_max 4.4-5.0 HTC One mini 2 HTC_M8MINx 4.4-6.0 HTC One X9 HTC_X9u 6.0 HTC One® (M8) HTC One_M8 4.4-6.0 HTC One® (M8) HTC_M8 4.4-6.0 HTC One® (M8) HTC_M8x 4.4-6.0 Nexus 9 Nexus 9 5.0-6.0 HUAWEI LG HUAWEI GRA- P8 6.0 AKA LG-H788n 4.4 L09 P8 Lite HUAWEI ALE-L21 5.0 F90 -

Electronic 3D Models Catalogue (On July 26, 2019)
Electronic 3D models Catalogue (on July 26, 2019) Acer 001 Acer Iconia Tab A510 002 Acer Liquid Z5 003 Acer Liquid S2 Red 004 Acer Liquid S2 Black 005 Acer Iconia Tab A3 White 006 Acer Iconia Tab A1-810 White 007 Acer Iconia W4 008 Acer Liquid E3 Black 009 Acer Liquid E3 Silver 010 Acer Iconia B1-720 Iron Gray 011 Acer Iconia B1-720 Red 012 Acer Iconia B1-720 White 013 Acer Liquid Z3 Rock Black 014 Acer Liquid Z3 Classic White 015 Acer Iconia One 7 B1-730 Black 016 Acer Iconia One 7 B1-730 Red 017 Acer Iconia One 7 B1-730 Yellow 018 Acer Iconia One 7 B1-730 Green 019 Acer Iconia One 7 B1-730 Pink 020 Acer Iconia One 7 B1-730 Orange 021 Acer Iconia One 7 B1-730 Purple 022 Acer Iconia One 7 B1-730 White 023 Acer Iconia One 7 B1-730 Blue 024 Acer Iconia One 7 B1-730 Cyan 025 Acer Aspire Switch 10 026 Acer Iconia Tab A1-810 Red 027 Acer Iconia Tab A1-810 Black 028 Acer Iconia A1-830 White 029 Acer Liquid Z4 White 030 Acer Liquid Z4 Black 031 Acer Liquid Z200 Essential White 032 Acer Liquid Z200 Titanium Black 033 Acer Liquid Z200 Fragrant Pink 034 Acer Liquid Z200 Sky Blue 035 Acer Liquid Z200 Sunshine Yellow 036 Acer Liquid Jade Black 037 Acer Liquid Jade Green 038 Acer Liquid Jade White 039 Acer Liquid Z500 Sandy Silver 040 Acer Liquid Z500 Aquamarine Green 041 Acer Liquid Z500 Titanium Black 042 Acer Iconia Tab 7 (A1-713) 043 Acer Iconia Tab 7 (A1-713HD) 044 Acer Liquid E700 Burgundy Red 045 Acer Liquid E700 Titan Black 046 Acer Iconia Tab 8 047 Acer Liquid X1 Graphite Black 048 Acer Liquid X1 Wine Red 049 Acer Iconia Tab 8 W 050 Acer -

Phone Compatibility
Phone Compatibility • Compatible with iPhone models 4S and above using iOS versions 7 or higher. Last Updated: February 14, 2017 • Compatible with phone models using Android versions 4.1 (Jelly Bean) or higher, and that have the following four sensors: Accelerometer, Gyroscope, Magnetometer, GPS/Location Services. • Phone compatibility information is provided by phone manufacturers and third-party sources. While every attempt is made to ensure the accuracy of this information, this list should only be used as a guide. As phones are consistently introduced to market, this list may not be all inclusive and will be updated as new information is received. Please check your phone for the required sensors and operating system. Brand Phone Compatible Non-Compatible Acer Acer Iconia Talk S • Acer Acer Jade Primo • Acer Acer Liquid E3 • Acer Acer Liquid E600 • Acer Acer Liquid E700 • Acer Acer Liquid Jade • Acer Acer Liquid Jade 2 • Acer Acer Liquid Jade Primo • Acer Acer Liquid Jade S • Acer Acer Liquid Jade Z • Acer Acer Liquid M220 • Acer Acer Liquid S1 • Acer Acer Liquid S2 • Acer Acer Liquid X1 • Acer Acer Liquid X2 • Acer Acer Liquid Z200 • Acer Acer Liquid Z220 • Acer Acer Liquid Z3 • Acer Acer Liquid Z4 • Acer Acer Liquid Z410 • Acer Acer Liquid Z5 • Acer Acer Liquid Z500 • Acer Acer Liquid Z520 • Acer Acer Liquid Z6 • Acer Acer Liquid Z6 Plus • Acer Acer Liquid Zest • Acer Acer Liquid Zest Plus • Acer Acer Predator 8 • Alcatel Alcatel Fierce • Alcatel Alcatel Fierce 4 • Alcatel Alcatel Flash Plus 2 • Alcatel Alcatel Go Play • Alcatel Alcatel Idol 4 • Alcatel Alcatel Idol 4s • Alcatel Alcatel One Touch Fire C • Alcatel Alcatel One Touch Fire E • Alcatel Alcatel One Touch Fire S • 1 Phone Compatibility • Compatible with iPhone models 4S and above using iOS versions 7 or higher. -

HTC Desire 826 Dual Sim 2 Contents Contents
User guide HTC Desire 826 dual sim 2 Contents Contents What's new Android 6.0 Marshmallow 9 Software and app updates 10 Unboxing HTC Desire 826 11 nano UIM and nano SIM cards 12 Storage card 14 Battery 16 Switching the power on or off 16 Managing your nano UIM and nano SIM cards with Dual network manager 17 Phone setup and transfer Setting up HTC Desire 826 for the first time 18 Restoring content from HTC Backup 19 Transferring content from an Android phone 19 Ways of transferring content from an iPhone 20 Transferring iPhone content through iCloud 20 Transferring contacts from your old phone through Bluetooth 20 Other ways of getting contacts and other content 21 Transferring photos, videos, and music between your phone and computer 22 Using Quick Settings 22 Getting to know your settings 24 Updating your phone's software 24 Getting apps from Google Play 26 Downloading apps from the web 27 Uninstalling an app 28 Your first week with your new phone Basics 29 HTC Sense Home widget 37 Lock screen 39 Notifications 42 Working with text 43 HTC Help 47 Phone calls Making a call with Smart dial 48 3 Contents Making a call with your voice 48 Dialing an extension number 49 Returning a missed call 49 Speed dial 49 Calling a number in a message, email, or calendar event 49 Making an emergency call 50 Receiving calls 50 What can I do during a call? 50 Setting up a conference call (GSM) 51 Call History 52 Switching between silent, vibrate, and normal modes 52 Home dialing 53 Messages Sending a text message (SMS) 54 Sending a multimedia message (MMS) -

Factory Model Device Model
Factory Model Device Model Acer A1-713 acer_aprilia Acer A1-830 Avvio_753 Acer A1-830 X958E Acer A3-A20 8675 Acer Acer E320-orange C6 Acer Acer E320-orange Oysters T72MR 3G Acer AT390 QMobile i10 Acer AT390 T2 Acer AT390 Xiaomi Acer B1-723 oban Acer B1-730 a29 Acer B1-820 i-mobile2.8 Acer CloudMobile S500 a9 Acer DA220HQL gilda_p8081 Acer DA226HQ sm618_w_ztc_72lca Acer E120 K2 Acer E310 lava75_cu_jb Acer E330 A37 Acer E330 C7 Acer E330 G910 Acer E330 msm8x25q_d5 Acer E330 Z50_Nova Acer E350 C8n Acer G100W F13 Acer Iconia Tab 7 acer_apriliahd Acer Iconia Tab A211 g12refM805 Acer Iconia Tab A211 MYPHONE_AGUA_OCEAN_MINI Acer Iconia Tab A501 E353I Acer Iconia Tab A510 K235 Acer Iconia TalkTab 7 acer_a1_724 Acer Iconia TalkTab 7 d3268_ctp_q_mobile Acer Liquid a1 Acer Liquid C1 I1 Acer Liquid C1 s620_f_h1_trx_j401_ec Acer Liquid E1 C10 Acer Liquid E2 C11 Acer Liquid E3 acer_e3 Acer Liquid E3 acer_e3n Acer Liquid E3 D7.2 3G Acer Liquid E3 hedy89_we_jb2 Acer Liquid E3 SOLO Acer Liquid E600 e600 Acer Liquid E600 S5J Acer Liquid E600 z3368 Acer Liquid E700 acer_e39 Acer Liquid Gallant E350 C8 Acer Liquid Jade acer_S55 Acer Liquid Jade S acer_S56 Acer Liquid Jade Z ABCD Acer Liquid Jade Z acer_S57 Acer Liquid Jade Z k002_gfen Acer Liquid Jade Z mobiistar BUDDY Acer Liquid Mini Bmobile.AX800 Acer Liquid Mini C4R Acer Liquid S1 a10 Acer Liquid S2 a12 Acer Liquid S2 B706 Acer Liquid S3 FIREFLY_S10DUAL Acer Liquid S3 s3 Acer Liquid X2 acer_S59 Acer Liquid X2 g517_d1e_less26 Acer Liquid Z200 A1000s Acer Liquid Z200 acer_z200 Acer Liquid Z200 s9201b Acer -

Fnac Reprise
FNAC REPRISE Liste des smartphones éligibles au programme de reprise au 19/08/2016 ACER LIQUID Z4 APPLE IPHONE 5 BLACK 64GB ACER INCORPORATED LIQUID Z530S APPLE IPHONE 5 WHITE 16GB ACER INCORPORATED LIQUID Z630S APPLE IPHONE 5 WHITE 32GB ALBA ALBA 4.5INCH 5MP 4G 8GB APPLE IPHONE 5 WHITE 64GB ALBA DUAL SIM APPLE IPHONE 5C ALCATEL IDOL 3 8GB APPLE IPHONE 5C BLUE 16GB ALCATEL ONE TOUCH 228 APPLE IPHONE 5C BLUE 32GB ALCATEL ONE TOUCH 903 APPLE IPHONE 5C BLUE 8GB ALCATEL ONE TOUCH 903X APPLE IPHONE 5C GREEN 16GB ALCATEL ONE TOUCH IDOL 2 MINI S APPLE IPHONE 5C GREEN 32GB ALCATEL ONE TOUCH TPOP APPLE IPHONE 5C GREEN 8GB ALCATEL ONETOUCH POP C3 APPLE IPHONE 5C PINK 16GB AMAZON FIRE PHONE APPLE IPHONE 5C PINK 32GB APPLE APPLE WATCH EDITION 42MM APPLE IPHONE 5C PINK 8GB APPLE IPHONE 3G APPLE IPHONE 5C WHITE 16GB APPLE IPHONE 3G BLACK 16GB APPLE IPHONE 5C WHITE 32GB APPLE IPHONE 3G BLACK 8GB APPLE IPHONE 5C WHITE 8GB APPLE IPHONE 3G WHITE 16GB APPLE IPHONE 5C YELLOW 16GB APPLE IPHONE 3GS APPLE IPHONE 5C YELLOW 32GB APPLE IPHONE 3GS 8GB APPLE IPHONE 5C YELLOW 8GB APPLE IPHONE 3GS BLACK 16GB APPLE IPHONE 5S APPLE IPHONE 3GS BLACK 32GB APPLE IPHONE 5S BLACK 16GB APPLE IPHONE 3GS WHITE 16GB APPLE IPHONE 5S BLACK 32GB APPLE IPHONE 3GS WHITE 32GB APPLE IPHONE 5S BLACK 64GB APPLE IPHONE 4 APPLE IPHONE 5S GOLD 16GB APPLE IPHONE 4 BLACK 16GB APPLE IPHONE 5S GOLD 32GB APPLE IPHONE 4 BLACK 32GB APPLE IPHONE 5S GOLD 64GB APPLE IPHONE 4 BLACK 8GB APPLE IPHONE 5S WHITE 16GB APPLE IPHONE 4 WHITE 16GB APPLE IPHONE 5S WHITE 32GB APPLE IPHONE 4 WHITE 32GB APPLE IPHONE -

ETUI W Kolorze Czarnym ALCATEL A3
ETUI w kolorze czarnym ALCATEL A3 5.0'' CZARNY ALCATEL PIXI 4 4.0'' 4034A CZARNY ALCATEL PIXI 4 5.0'' 5045X CZARNY ALCATEL POP C3 4033A CZARNY ALCATEL POP C5 5036A CZARNY ALCATEL POP C7 7041X CZARNY ALCATEL POP C9 7047D CZARNY ALCATEL U5 5044D 5044Y CZARNY HTC 10 CZARNY HTC DESIRE 310 CZARNY HTC DESIRE 500 CZARNY HTC DESIRE 516 CZARNY HTC DESIRE 610 CZARNY HTC DESIRE 616 CZARNY HTC DESIRE 626 CZARNY HTC DESIRE 650 CZARNY HTC DESIRE 816 CZARNY HTC ONE A9 CZARNY HTC ONE A9s CZARNY HTC ONE M9 CZARNY HTC U11 CZARNY HUAWEI ASCEND G510 CZARNY HUAWEI ASCEND Y530 CZARNY HUAWEI ASCEND Y600 CZARNY HUAWEI G8 GX8 CZARNY HUAWEI HONOR 4C CZARNY HUAWEI HONOR 6X CZARNY HUAWEI HONOR 7 LITE 5C CZARNY HUAWEI HONOR 8 CZARNY HUAWEI HONOR 9 CZARNY HUAWEI MATE 10 CZARNY HUAWEI MATE 10 LITE CZARNY HUAWEI MATE 10 PRO CZARNY HUAWEI MATE S CZARNY HUAWEI P10 CZARNY HUAWEI P10 LITE CZARNY HUAWEI P10 PLUS CZARNY HUAWEI P8 CZARNY HUAWEI P8 LITE 2017 CZARNY HUAWEI P8 LITE CZARNY HUAWEI P9 CZARNY HUAWEI P9 LITE CZARNY HUAWEI P9 LITE MINI CZARNY HUAWEI Y3 2017 CZARNY HUAWEI Y3 II CZARNY HUAWEI Y5 2017 Y6 2017 CZARNY HUAWEI Y5 Y560 CZARNY HUAWEI Y520 Y540 CZARNY HUAWEI Y541 CZARNY HUAWEI Y6 II CZARNY HUAWEI Y625 CZARNY HUAWEI Y7 CZARNY iPHONE 5C CZARNY iPHONE 5G CZARNY iPHONE 6 4.7'' CZARNY iPHONE 7 4.7'' 8 4.7'' CZARNY iPHONE 7 PLUS 5.5'' 8 PLUS CZARNY iPHONE X A1865 A1901 CZARNY LENOVO K6 NOTE CZARNY LENOVO MOTO C CZARNY LENOVO MOTO C PLUS CZARNY LENOVO MOTO E4 CZARNY LENOVO MOTO E4 PLUS CZARNY LENOVO MOTO G4 XT1622 CZARNY LENOVO VIBE C2 CZARNY LENOVO VIBE K5 CZARNY -

Elenco Device Android.Xlsx
Manufacturer,Model Name,Model Code,RAM (TotalMem),Form Factor,System on Chip,Screen Sizes,Screen Densities,ABIs,Android SDK Versions,OpenGL ES Versions 10.or,10or_G2,G2,3742-5747MB,Phone,Qualcomm SDM636,1080x2246,480,arm64-v8a 10.or,E,E,1857-2846MB,Phone,Qualcomm MSM8937,1080x1920,480,arm64-v8a 10.or,G,G,2851-3582MB,Phone,Qualcomm MSM8953,1080x1920,480,arm64-v8a 10.or,D,10or_D,2868-2874MB,Phone,Qualcomm MSM8917,720x1280,320,arm64-v8a 7mobile,SWEGUE,SWEGUE,1836MB,Phone,Mediatek MT6737T,1080x1920,480,arm64-v8a 7mobile,Kamba 2,7mobile_Kamba_2,2884MB,Phone,Mediatek MT6739CH,720x1440,320,arm64-v8a A1,A1 Alpha 20+,P671F60,3726MB,Phone,Mediatek MT6771T,1080x2340,480,arm64-v8a Accent,FAST10,FAST10,1819MB,Tablet,Spreadtrum SC9863A,1280x800,213,arm64-v8a ACE France,BUZZ 2,BUZZ_2,850MB,Phone,Spreadtrum SC9863A,720x1560,320,armeabi-v7a ACE France,BUZZ 2,BUZZ_2_Plus,1819MB,Phone,Spreadtrum SC9863A,720x1560,320,arm64-v8a ACE France,URBAN 2,URBAN_2,2824MB,Phone,Spreadtrum SC9863A,720x1560,320,arm64-v8a ACE France,AS0518,AS0518,1822MB,Phone,Mediatek MT6762,720x1440,320,arm64-v8a ACE France,URBAN 1,URBAN_1,1839MB,Phone,Mediatek MT6739WA,720x1440,320,arm64-v8a ACE France,AS0618,AS0618,2826MB,Phone,Mediatek MT6752,720x1500,320,arm64-v8a Acer,Iconia Tab 10,acer_asgard,1970MB,Tablet,Mediatek MT8176A,800x1280,160,arm64-v8a Acer,Iconia Tab 10,acer_asgardfhd,1954MB,Tablet,Mediatek MT8167B,1920x1200,240,arm64-v8a Acer,Iconia Tab 10,acer_Titan,3959MB,Tablet,Mediatek MT8176A,1200x1920,240,arm64-v8a Acer,Liquid Z530S,acer_t05,2935MB,Phone,Mediatek MT6753,720x1280,320,arm64-v8a