DOCSLIB.ORG

Glitches in Superfluid Neutron Stars

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Glitches in Superfluid Neutron Stars GLITCHES IN SUPERFLUID NEUTRON STARS Marco Antonelli [email protected] Centrum Astronomiczne im. Mikołaja Kopernika Polskiej Akademii Nauk Quantum Turbulence: Cold Atoms, Heavy Ions ans Neutron Stars INT, Seattle (WA) – April 16, 2019 Outline Summary: Why glitches (in radio pulsars) tell us something about rotating neutron stars? - A bit of hystory: why superfluidity is needed to explain glitches. Intrinsic difficulty: model the exchange of angular momentum that causes the glitch (mutual friction) - Many-scales (coherence length → stellar radius) - Possible memory effects (also observed in He-II experiments) Which microscopic input do we need? I will focus on two quantities: - Pinning forces (or better, the critical current for unpinning) - Entrainment Is it possible to use glitches to obtain “model-independent” statements about neutron stars interiors? SPOILER: yes, we have at the moment 2 models: 1 – Activity test → “entrainment” 2 – Largest glitch test → “pinning forces” Question: is it possible to go beyond these two tests? What can be done? Neutron stars – RPPs What we observe, since: What we think it is, since: Hewish, Bell et al., Observation of a rapidly pulsating Pacini, Energy emission from a neutron star (1967) radio source (1968) Gold, Rotating neutron stars as the origin of the pulsating radio sources (1968) Magnetic field lines Radiation beam Coordinated observations with three telescopes: 22-s data slice of the pulsed radiation at four different radio Open issue: precise description bands obtained of the 1.2 s pulsar B1113+16. of beamed emission mechanism Why? Coherent (i.e. non-thermal) emission + brightness + small period: only possible for very compact objects A vibrating WD or NS? excluded by pulsar-timing data: P increases with time. BH accretion? No regular pulses... SOLUTION: pulsars are strongly magnetized rotating neutrons stars. Neutron stars - structure Sketch of nuclear matter phase diagram What we can not observe: internal structure Main idea: compressing matter liberates degrees of freedom. Gravity, holds the star together Electromagnetism, makes pulsars pulse and magnetars flare Strong interaction, determines the internal composition and prevents gravitational collapse Weak interaction, determines the internal composition and affects reaction rates (chemical equilibrium and neutrino cooling) Neutron stars – M-R relation TOV equations: hydrostatic equilibrium in GR TOV inversion: Lindblom, ApJ 398, 569 (1992) EOS lines not intersecting the J1614-2230 band are ruled out. Rotation increases the maximum possible mass for each EOS: ≲2% correction for P~3 ms. Demorest et al. Nature 467 (2010) Shapiro delay forPSR J1614-2230 PB Demorest Residuals “with GR” Residuals “without GR” Shapiro delay functional form In In contrast withX-ray-based mass/radius measurements,Shapiro delay providesno information about the NS radius. et al. Nature 467 ,1081-1083 (2010) (0.500±0.006) M helium-carbon-oxygen WD Companion: andthe companion. infer the masses of both the neutron pulsar star systems, Shapiro delay For allows to nearly edge-on millisecond radio (1.97±0.04) M Millisecond pulsar ⊙ ⊙ Shapiro delay: high-mass MSP J0740-6620 Cromartie et al. arXiv:1904.06759 A very massive neutron star: relativistic Shapiro delay measurements of PSR J0740+6620 12-year data set yielded a pulsar mass of 2.17+/-0.10 MSun at 68.3% credibility. Modeling the thermal pulse profile of this MSP at X-ray energies will aid in constraining both M and R. Pulsartiming Period derivative ( s/s ) Infer red feld ma gnet Perio ic d d ( s ) derivative) are precisely determined. Period P and spin-down rate (period a very small glitch in a binary system). magnetars and millisecond pulsars and catalogue (including few glitches in objects reported in To date the ~500 Jodrell glitch Bank events irregularities (glitches). in ~170 down... except Stable clocks for with random predictable timing spin- the second derivative ofis P needed. Sanity check from the braking index, but B). regions (inferred age and magnetic field Different classes populate different Pulsar glitches “Lack” of radiative/pulse profile changes (in RPPs): → Evidence for internal origin Vela: almost no recovery Long recoveries: → Impossible to explain if viscosity is present Diverse phenomenology in RPPs: → probably due to different age (temperature), mass, rotational parameters... Crab: nearly complete recovery Key point: to describe glitches we need that a NS is comprised of (at least) two components that exchange angular momentum. Can we identify the (two?) components ? Which part of the NS provides the angular momentum needed to spin-up the “observable component” ? Starquake model Ruderman, Nature 223, 597 (1969) Liquid interior The quake causes a sudden rearrangement of the moment of inertia and ultimately a glitch. With this model it is possible to explain only the “jump”, not the subsequent relaxation. Further problem: according to this theory, glitches should be rare: Baym&Pines, Ann. Phys. 66 (1971) ( in the Vela every ~3 yrs, not enough time to develop stresses, Giliberti et al. arXiv:1902.06345 ) Glitch recovery The recovery from glitches in not uniform: - Sometimes an “exponential” relaxation is observed, sometimes a “step-like” increase of the frequency. - Both behaviours can be seen in the same object! The instantaneous jump may be described in terms of a sudden rearrangement of the star crust, but not the recover. We need another ingredient (the superfluid) to describe glitches. Two-component model Baym et al. “Spin Up in Neutron Stars : The Future of the Vela Pulsar”, Nature (1969) The long recovery time-scales (of order months) observed after the first Vela glitch were considered to be evidence for a weakly coupled superfluid component in the stellar interior. Superfluidity → “no viscosity” → long relaxation timescale “crust” “neutrons” bra tor ki qu ng e (“mu Intern tual f al to rictio rque n”) Neutron drip → Inner core? → Two-component model Two-component Superfluidity → “no viscosity” → long relaxation timescale the stellar interior. evidence for a weakly coupled superfluid component in observed after glitch the were first considered Vela to be The long recovery time-scales (of order months) Baym etal. “SpinPulsar”, Nature Up (1969)in Neutron FutureTheStars : ofthe Vela “c “n rust eutr ” ons” bra tor qu ki ng e (“mu Intern tual f al toal rictio rque n”) (too much oblateness and building stress rate needed) → → Coupling timescale: fitted from post-glitch relaxation. the “healing parameter” Q. the change in the moment of inertia sets the amplitude and Spin-up is given by the settling of the crust (starquake): Still problems with very large glitches Relaxation is always exponential -5 Angular velocity (~10 rad/s) # o s t - g l i t c $ s % i n - d o w n m o d e l !"servational # "lac windor w e - Time (~wee s) (~wee Time g l i t c $ s % i n - d o w n (1-Q) m o d e ΔΩ l gl ΔΩ gl (1-Q) Q ΔΩ gl ΔΩ gl Glitch mechanism (vortex mediated) Anderson & Itoh Pulsar glitches and restlessness as a hard superfluidity phenomenon (1975) - The charged component steadily looses angular momentum t x s e - Vortices are pinned the superfluid cannot spin-down a t p r o w v o l → vortex line carried by the charged component a F → a velocity lag builds up → neutron current in the frame of the normal component Magnus force - Magnus force ≃ pinning force: the vortex line unpins → analogy between unpinning lag and critical current in superconductors → vortices can move: mutual friction between the components Expulsion of vortex lines from bulk superfluid Local: vortex creep Global: vortex avalanche (thermally activated) (trigger?) Analogy: “noisiness” in superconductors velocity of flux-lines S. Field et al. Superconducting Vortex Avalanches (1995) velocity of flux-lines “Strong pinning regimes by spherical inclusions in anisotropic type-II superconductors” R. Willa et al. (2018) In the complete phase diagram of the dynamical phases also the variable J should be considered! Hydrodynamics in neutron stars The dynamics of vortices is hidden inside this term. Pinning modifies the mutual friction (when all vortices are perfectly pinned the mutual friction is zero) (x = n or p) Assumption: the charged component Widely used approximation: (and possibly the superfluid core) circular flow (no meridional circulation) rotates as a rigid body On the other hand, the superfluid in the crust can rotate non-uniformly. - - - - Entrainment coupling: crustand core In the core: the In In the crust: the In → Alpar et al. coupled to the crust on the timescale of a second. → - Local effect: m*<1 different mechanism: actually - Very idea similarmore toA&B the original - Entrainment is due to the strong interaction between protons and neutrons star core, Chamel N., Haensel P. for pulsar glitch theory. component: reduced mobility of free neutrons is a potential problem → - Bragg scattering by crustal lattice, non-local effect: m* > 1 the framework of the band theory of solids, Chamel N. Consequence #2: Dipole-dipole interaction with flux-tubes (core pinning?) Consequence #1: Scattering of electrons off vortex cores: the core is Consequence: the crustal superfluid is entrained by the normal Phys. Rev. C 73 (2006). Phys. Rev. Neutron conduction in the inner crust of a neutron star in Rapid postglitch spin-up of the superfluid core in pulsars(1984) Entrainment parameters in a cold superfluid neutron Phys Rev C 85 (2012) Core of the vortex line Attached magnetic field E Vortex n d t I r line n r a d a t i h g n u e g e c e d e n d d p e v r u e o e t l t r e l o o o c n n c t r s i t o f y l n a u f s n i d i d e l d i n Test #1: entrainment Entrainment parameters: Chamel, N.
Load more

Recommended publications
  • Timing Behavior of the Magnetically Active Rotation-Powered Pulsar in the Supernova Remnant Kesteven 75
    https://ntrs.nasa.gov/search.jsp?R=20090038692 2019-08-30T08:05:59+00:00Z View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NASA Technical Reports Server Timing Behavior of the Magnetically Active Rotation-Powered Pulsar in the Supernova Remnant Kesteven 75 Margaret A. Livingstone 1 , Victoria M. Kaspi Department of Physics, Rutherford Physics Building, McGill University, 3600 University Street, Montreal, Quebec, H3A 2T8, Canada and Fotis. P. Gavriil NASA Goddard Space Flight Center, Astrophysics Science Division, Code 662, Greenbelt, MD 20771 Center for Research and Exploration in Space Science and Technology, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21 250 ABSTRACT We report a large spin-up glitch in PSR J1846-0258 which coincided with the onset of magnetar-like behavior on 2006 May 31. We show that the pul- sar experienced an unusually large glitch recovery, with a recovery fraction of Q = 5.9 ± 0.3, resulting in a net decrease of the pulse frequency. Such a glitch recovery has never before been observed in a rotation-powered pulsar, however, similar but smaller glitch over-recovery has been recently reported in the magne- tar AXP 4U 0142+61 and may have occurred in the SGR 1900+14. We discuss the implications of the unusual timing behavior in PSR J1846-0258 on its status as the first identified magnetically active rotation-powered pulsar. Subject headings: pulsars: general—pulsars: individual (PSR J1846-0258)—X- rays: stars 1. Introduction PSR J1846-0258 is a. young (-800 yr), 326 ms pulsar, discovered in 2000 with the Rossi X-ray Timing Explorer (RXTE; Gotthelf et al.
    [Show full text]
  • Rotational Glitches in Radio Pulsars and Magnetars
    UvA-DARE (Digital Academic Repository) Rotational glitches in radio pulsars and magnetars Antonopoulou, D. Publication date 2015 Document Version Final published version Link to publication Citation for published version (APA): Antonopoulou, D. (2015). Rotational glitches in radio pulsars and magnetars. General rights It is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), other than for strictly personal, individual use, unless the work is under an open content license (like Creative Commons). Disclaimer/Complaints regulations If you believe that digital publication of certain material infringes any of your rights or (privacy) interests, please let the Library know, stating your reasons. In case of a legitimate complaint, the Library will make the material inaccessible and/or remove it from the website. Please Ask the Library: https://uba.uva.nl/en/contact, or a letter to: Library of the University of Amsterdam, Secretariat, Singel 425, 1012 WP Amsterdam, The Netherlands. You will be contacted as soon as possible. UvA-DARE is a service provided by the library of the University of Amsterdam (https://dare.uva.nl) Download date:06 Oct 2021 Rotational glitches in radio pulsars and magnetars ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit van Amsterdam op gezag van de Rector Magnificus prof. dr. D. C. van den Boom ten overstaan van een door het college voor promoties ingestelde commissie, in het openbaar te verdedigen in de Agnietenkapel op woensdag 21 januari 2015, te 14:00 uur door Danai Antonopoulou geboren te Athene, Griekenland Promotiecommissie Promotor: prof.
    [Show full text]
  • Study of Pulsar Wind Nebulae in Very-High-Energy Gamma-Rays with H.E.S.S
    Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S. Michelle Tsirou To cite this version: Michelle Tsirou. Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S.. As- trophysics [astro-ph]. Université Montpellier, 2019. English. NNT : 2019MONTS096. tel-02493959 HAL Id: tel-02493959 https://tel.archives-ouvertes.fr/tel-02493959 Submitted on 28 Feb 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE POUR OBTENIR LE GRADE DE DOCTEUR DE L’UNIVERSITÉ DE MONTPELLIER En Astrophysiques École doctorale I2S Unité de recherche UMR 5299 Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S. Présentée par Michelle TSIROU Le 17 octobre 2019 Sous la direction de Yves A. GALLANT Devant le jury composé de Elena AMATO, Chercheur, INAF - Acetri Rapporteur Arache DJANNATI-ATAȈ, Directeur de recherche, APC - Paris Examinateur Yves GALLANT, Directeur de recherche, LUPM - Montpellier Directeur de thèse Marianne LEMOINE-GOUMARD, Chargée de recherche, CENBG - Bordeaux Rapporteur Alexandre MARCOWITH, Directeur de recherche, LUPM - Montpellier Président du jury Study of Pulsar Wind Nebulae in Very-High-Energy gamma-rays with H.E.S.S.1 Michelle Tsirou 1High Energy Stereoscopic System To my former and subsequent selves, may this wrenched duality amalgamate ultimately.
    [Show full text]
  • The Glitch Activity of Neutron Stars J
    A&A 608, A131 (2017) Astronomy DOI: 10.1051/0004-6361/201731519 & c ESO 2017 Astrophysics The glitch activity of neutron stars J. R. Fuentes1, C. M. Espinoza2, A. Reisenegger1, B. Shaw3, B. W. Stappers3, and A. G. Lyne3 1 Instituto de Astrofísica, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile e-mail: [email protected] 2 Departamento de Física, Universidad de Santiago de Chile, Avenida Ecuador 3493, 9170124 Estación Central, Santiago, Chile 3 Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, The University of Manchester, Manchester M13 9PL, UK Received 6 July 2017 / Accepted 3 October 2017 ABSTRACT We present a statistical study of the glitch population and the behaviour of the glitch activity across the known population of neutron stars. An unbiased glitch database was put together based on systematic searches of radio timing data of 898 rotation-powered pulsars obtained with the Jodrell Bank and Parkes observatories. Glitches identified in similar searches of 5 magnetars were also included. The database contains 384 glitches found in the rotation of 141 of these neutron stars. We confirm that the glitch size distribution is at least bimodal, with one sharp peak at approximately 20 µHz, which we call large glitches, and a broader distribution of smaller glitches. We also explored how the glitch activityν ˙g, defined as the mean frequency increment per unit of time due to glitches, correlates with the spin frequency ν, spin-down rate jν˙j, and various combinations of these, such as energy loss rate, magnetic field, and spin-down age.
    [Show full text]
  • Magnetars: Pion Condensates in the Sky?
    Magnetars: Pion Condensates in the Sky? N.D. Hari Dass TIFR-TCIS, Hyderabad In collaboration with V. Soni(Jamia) & Dipankar Bhattacharya(IUCAA) IWARA 2018, Ollantaytambo, Peru. N.D. Hari Dass Magnetars & Pion Condensates Some References N.D. Hari Dass and V. Soni, Mon. Not. Royal Astron. Soc., 425, 1558-1566 (2012). H.B. Nielsen and V. Soni, Phys. Lett. B726, 41-44 (2013). N.D. Hari Dass Magnetars & Pion Condensates Neutron Stars Nuclear density ρ 2:8 1014gm=cm3. Equivalently 0 ' n 0:17nucleons=fermi3. 0 ' Stable neutron stars can have masses in the range 0.1 solar mass to 2 solar masses. Most observed pulsars have masses about 1.4 solar masses. Neutron stars produced in core collapse are expected with this mass. Heavier neutron stars are believed to be as a result of acretion later on. Typical radii of NS are 10 - 20 kms. Neutron stars can be thought of as giant nuclei with A 1057! ' N.D. Hari Dass Magnetars & Pion Condensates Neutron Star Structure Density ρ decreases as one moves outwards from the centre. The outer kilometre or so is the Crust. It consists of a lattice of bare nuclei and a degenerate electron gas. Next to the crust is a superfluid layer and vortices here contribute to the angular momentum of the star. These vortices also play an important role in the so called glitches whence the star actually speeds up. The least understood part is the core of the NS. Density here can be in the range of 3-10 times nuclear density. It is also very hot.
    [Show full text]
  • Statistical Properties of the Repeating Fast Radio Burst Source FRB 121102
    ISSN: 2641-886X International Journal of Cosmology, Astronomy and Astrophysics Research Article Open Access Statistical properties of the repeating fast radio burst source FRB 121102 Bing Li1-3*, Long-Biao Li4, Zhi-Bin Zhang5, Jin-Jun Geng1,6, Li-Ming Song2,3, Yong-Feng Huang1,6* and Yuan-Pei Yang7,8 1School of Astronomy and Space Science, Nanjing University, Nanjing 210023, China 2Laboratory for Particle Astrophysics, Institute of High Energy Physics, Beijing 100049, China 3Key Laboratory of Particle Astrophysics, Chinese Academy of Sciences, Beijing 100049, China 4School of Mathematics and Physics, Hebei University of Engineering, Handan 056005, China 5College of Physics and Engineering, Qufu Normal University, Qufu 273165, China 6Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, China 7Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, China 8National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China Article Info Abstract *Corresponding authors: Currently, FRB 121102 is the only fast radio burst source that was observed to give Bing Li out bursts repeatedly. It shows a high repeating rate, with more than one hundred bursts School of Astronomy and Space Science Nanjing University being spotted, but with no obvious periodicity in the activities. Thanks to its repetition, Nanjing 210023, China the source was well localized with a subarcsecond accuracy, leading to a red shift E-mail: [email protected] measurement of about 0.2. FRB 121102 is a unique source that can help us understand Yong-Feng Huang the enigmatic nature of fast radio bursts. In this study, we analyze the characteristics of Professor the waiting times between bursts from FRB 121102.
    [Show full text]
  • Properties of the Binary Neutron Star Merger GW170817
    Properties of the Binary Neutron Star Merger GW170817 The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Abbott, B.P. et al. “Properties of the Binary Neutron Star Merger GW170817.” Physical Review X 9, 1 (January 2019): 11001 © 2019 The Authors As Published http://dx.doi.org/10.1103/PhysRevX.9.011001 Publisher American Physical Society Version Final published version Citable link https://hdl.handle.net/1721.1/121211 Detailed Terms https://creativecommons.org/licenses/by/4.0/ PHYSICAL REVIEW X 9, 011001 (2019) Properties of the Binary Neutron Star Merger GW170817 B. P. Abbott et al.* (LIGO Scientific Collaboration and Virgo Collaboration) (Received 6 June 2018; revised manuscript received 20 September 2018; published 2 January 2019) On August 17, 2017, the Advanced LIGO and Advanced Virgo gravitational-wave detectors observed a low-mass compact binary inspiral. The initial sky localization of the source of the gravitational-wave signal, GW170817, allowed electromagnetic observatories to identify NGC 4993 as the host galaxy. In this work, we improve initial estimates of the binary’s properties, including component masses, spins, and tidal parameters, using the known source location, improved modeling, and recalibrated Virgo data. We extend the range of gravitational-wave frequencies considered down to 23 Hz, compared to 30 Hz in the initial analysis. We also compare results inferred using several signal models, which are more accurate and incorporate additional physical effects as compared to the initial analysis. We improve the localization of the gravitational-wave source to a 90% credible region of 16 deg2.
    [Show full text]
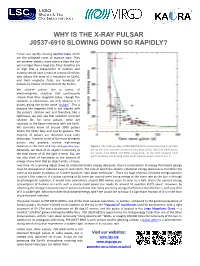
  • Why Is the X-Ray Pulsar J0537-6910 Slowing Down So Rapidly?
    WHY IS THE X-RAY PULSAR J0537-6910 SLOWING DOWN SO RAPIDLY? Pulsars are rapidly-rotating neutron stars, which are the collapsed cores of massive stars. They are extreme objects, more massive than the Sun yet no larger than a large city. Their densities are so high that a teaspoonful of neutron star material would have a mass of around 10 million tons (about the mass of a mountain on Earth), and their magnetic fields are hundreds of millions to trillions of times that of the Earth’s. We observe pulsars due to beams of electromagnetic radiation that continuously stream from their magnetic poles. Though this radiation is continuous, we only observe it in pulses, giving rise to the name “pulsars”. This is because the magnetic field is not aligned with the pulsar's rotation axis and therefore, like a lighthouse, we only see that radiation once per rotation (or, for some pulsars, twice per rotation) as the beam intersects with the Earth. We currently know of around 3000 pulsars within the Milky Way and nearby galaxies. The majority of pulsars are observed using radio telescopes, however some of the most energetic pulsars also produce intense high-energy radiation in the form of X-rays and gamma-rays. Figure 1: The braking index of PSR J0537-6910 as measured using X-ray data Generally, we think of an object’s luminosity as during the time intervals between each pulsar glitch. Red and black points the total power of all the light it emits. But, we are values from NICER and RXTE, respectively.
    [Show full text]
  • Portuguese SKA White Book
    Portuguese SKA White Book Title Portuguese SKA White Book Cover Image credit: Square Kilometre Array Organisation Editorial Board Domingos Barbosa (Instituto de Telecomunicações) Sonia Antón (Universidade of Aveiro, Instituto de Telecomunicações) João Paulo Barraca (Instituto de Telecomunicações, Universidade of Aveiro) Miguel Bergano (Instituto de Telecomunicações) Alexandre Correia (Universidade de Coimbra) Dalmiro Maia (Faculdade de Ciências da Universidade do Porto) Valério Ribeiro (Instituto de Telecomunicações, Universidade de Aveiro) Publisher UA Editora – Universidade de Aveiro ISBN 978-972-789-637-0 Agradecemos o apoio financeiro da Infraestrutura de Investigação E-Ciência Sustentável com o Square Kilometre Array (ENGAGE SKA), referência POCI-01-0145-FEDER-022217, financiada pelo Programa Operacional Competitividade e Internacionalização (COMPETE 2020) e pela Fundação para a Ciência e Tecnologia (FCT), Portugal, o apoio do Instituto de Telecomunicações, da Faculdade de Ciências da Universidade do Porto, da Universidade de Aveiro, da Universidade de Coimbra e do TICE.PT. Este trabalho foi tambem apoiado pela FCT e MCTES através de fundos nacionais e quando aplicável cofinanciado pelo FEDER, no âmbito do Acordo de Parceria PT2020 no âmbito do projeto UID/EEA/50008/2019 e projectos UIDB/50008/2020-UIDP/50008/2020. We acknowledge financial support from Enabling Green E-science for the Square Kilometre Array Research Infrastructure (ENGAGE SKA), grant POCI-01-0145-FEDER-022217, funded by Programa Operacional Competitividade e Internacionalização (COMPETE 2020) and FCT, Portugal, and support from Instituto de Telecomunicações, Faculty of Sciences of University of Porto, University of Coimbra, University of Aveiro and TICE.PT. This work was also funded by the Portuguese Science Foundation (FCT) and Ministério da Ciência, Tecnologia e Ensino Superior (MCTES) through national funds and when applicable co-funded EU funds under the project UIDB/50008/2020-UIDP/50008/2020 and UID/EEA/50008/2019.
    [Show full text]
  • Accretion-Powered Pulsar Reveals Unique Timing Glitch 6 September 2017
    Accretion-powered pulsar reveals unique timing glitch 6 September 2017 stellar materials outwards into space and leaving behind an extremely dense and compact object; this could either be a white dwarf, a neutron star or a black hole. If a neutron star is left, it may have a very strong magnetic field and rotate extremely quickly, emitting a beam of light that can be observed when the beam points towards Earth, in much the same way as a lighthouse beam sweeping past an observer. To the observer on Earth, it looks as though the star is emitting pulses of light, hence the name 'pulsar'. Now a group of scientists from the Middle East Technical University and Ba?kent University in Turkey have discovered a sudden change in the rotation speed of the peculiar pulsar SXP 1062. These jumps in frequency, known as 'glitches', are commonly seen in isolated pulsars, but have so far never been observed in binary pulsars (pulsars orbiting with a companion white dwarf or neutron Composite image of the X-ray pulsar SXP 1062 star) such as SXP 1062. surrounded by the supernova remnant. The false-colour image combines X-ray (blue) and optical data (oxygen: green, hydrogen: red). Credit: ESA / XMM-Newton / L. Oskinova, University of Potsdam, Germany / M. Guerrero, Instituto de Astrofisica de Andalucia, Spain (X- ray); Cerro Tololo Inter-American Observatory / R. Gruendl & Y. H. Chu, University of Illinois at Urbana- Champaign, USA (optical). Credit: Royal Astronomical Society The discovery of the largest timing irregularity yet observed in a pulsar is the first confirmation that pulsars in binary systems exhibit the strange phenomenon known as a 'glitch'.
    [Show full text]
  • Title an Anti-Glitch in a Magnetar Author(S) Archibald, RF
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by HKU Scholars Hub Title An anti-glitch in a magnetar Archibald, R. F.; Kaspi, V. M.; Ng, SCY; Gourgouliatos, K. N.; Author(s) Tsang, D.; Scholz, P.; Beardmore, A. P.; Gehrels, N.; Kennea, J. A. Citation Nature, 2013, v. 497 n. 7451, p. 591-593 Issued Date 2013 URL http://hdl.handle.net/10722/186148 Rights Creative Commons: Attribution 3.0 Hong Kong License An Anti-Glitch in a Magnetar R. F. Archibald1, V. M. Kaspi1, C. -Y. Ng1,2, K. N. Gourgouliatos 1, D. Tsang1, P. Scholz1, A. P. Beardmore3, N. Gehrels4, & J. A. Kennea5 1Department of Physics, McGill University, Montreal QC, H3A 2T8, Canada 2Department of Physics, The University of Hong Kong, Pokfulam Road, Hong Kong 3Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK 4Astrophysics Science Division, NASA Goddard Space Flight Center, Greenbelt, MD 20771 USA 5Department of Astronomy and Astrophysics, 525 Davey Lab, Pennsylvania State University, Uni- versity Park, PA 16802, USA Magnetars are neutron stars showing dramatic X-ray and soft γ-ray outbursting behaviour that is thought to be powered by intense internal magnetic fields1. Like conventional young neutron stars in the form of radio pulsars, magnetars exhibit “glitches” during which angu- lar momentum is believed to be transferred between the solid outer crust and the superfluid component of the inner crust 2–4. Hitherto, the several hundred observed glitches in ra- dio pulsars5, 6 and magnetars7 have involved a sudden spin-up of the star, due presumably to the interior superfluid rotating faster than the crust.
    [Show full text]
  • A Fast Radio Burst Associated with a Galactic Magnetar
    A fast radio burst associated with a Galactic magnetar 1;2;3; 2 4 2 Authors: C. D. Bochenek ∗, V. Ravi , K. V. Belov , G. Hallinan , J. Kocz2;5, S. R. Kulkarni2 & D. L. McKenna6 1 Cahill Center for Astronomy and Astrophysics, MC 249-17, California Institute of Tech- nology, Pasadena CA 91125, USA. 2 Owens Valley Radio Observatory, MC 249-17, California Institute of Technology, Pasadena CA 91125, USA. 3 E-mail: [email protected]. 4 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA. 5 Department of Astronomy, University of California, Berkeley, CA 94720, USA. 6 Caltech Optical Observatories, MC 249-17, California Institute of Technology, Pasadena CA 91125, USA. arXiv:2005.10828v1 [astro-ph.HE] 21 May 2020 1 Since their discovery in 2007, much effort has been devoted to uncover- ing the sources of the extragalactic, millisecond-duration fast radio bursts (FRBs)1. A class of neutron star known as magnetars is a leading candidate source of FRBs. Magnetars have surface magnetic fields in excess of 1014 G, the decay of which powers a range of high-energy phenomena2. Here we present the discovery of a millisecond-duration radio burst from the Galactic magnetar SGR 1935+2154, with a fluence of 1:5 0:3 Mega-Jansky millisec- onds. This event, termed ST 200428A(=FRB 200428),± was detected on 28 April 2020 by the STARE2 radio array3 in the 1281{1468 MHz band. The isotropic-equivalent energy released in ST 200428A is 4 103 times greater than in any Galactic radio burst previously observed on× similar timescales.
    [Show full text]