DOCSLIB.ORG

The Aniline–Water and Aniline–Methanol Complexes in the S1 Excited State

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Aniline–Water and Aniline–Methanol Complexes in the S1 Excited State Chemical Physics 330 (2006) 138–145 www.elsevier.com/locate/chemphys The aniline–water and aniline–methanol complexes in the S1 excited state G. Piani a, M. Pasquini a,b,I.Lo´pez-Toco´n a,c, G. Pietraperzia a,b, M. Becucci a,b,*, E. Castellucci a,b a LENS, via N. Carrara 1, Polo Scientifico Universita` di Firenze, 50019 Sesto Fiorentino (FI), Italy b Dipartimento di Chimica, Universita` di Firenze, Firenze, Italy c Departamento de Quı´mica-Fı´sica, Universidad de Ma´laga, Spain Received 27 March 2006; accepted 2 August 2006 Available online 5 August 2006 Abstract We report an experimental and theoretical study on the properties of the aniline–water and aniline–methanol jet cooled complexes. In both complexes the ligand (H2OorCH3OH) is hydrogen bonded to aniline, the interaction taking place at the lone pair of the nitrogen, in the amino group. The S1 S0 electronic excitation spectrum in both cases exhibits a very broad and weak band, blue shifted with respect to the origin band of aniline by 700 cmÀ1. Ab initio calculations, at different levels of theory with the cc-pvdz electronic basis set, were performed on aniline–water and predict a strong binding energy decrease in the excited state and a large change in geometry, in agreement with experimental results. Ó 2006 Elsevier B.V. All rights reserved. 1. Introduction [3,4]. Recently, different authors have reported on the properties of the anisole–H2O complex [5–7]. The structure Recent studies have reported on the properties of com- of anisole closely resembles that of phenol: the only differ- plex formed by water with organic molecules in gas phase ence is the change of the OH group with the OCH3 group. supersonic expansion [1,2]. In most of the cases, water acts The electronic transition has practically the same character as a base and the complex is stable, both in the ground and for both molecules [8]. Instead, in the case of water com- in the first electronic excited state. In this respect a repre- plex formation the two systems behave quite differently sentative system is the phenol–water complex. In the phe- as water is binding as an acid to anisole. Therefore, due nol–H2O complex, water is bound as a base to the to the decrease of electron density with electronic excitation phenol OH group [1,3,4]. Due to the changes in the elec- in the oxygen atom lone pairs, the origin of the electronic tronic density with the electronic transition, the hydrogen transition for the complex is blue shifted with respect to bond is stronger in the excited state with respect to the the anisole monomer and the hydrogen bond distance ground state. A measure of this change in the interaction increases. A discussion is still open on the nature of the energy is given by the red shift of the electronic transition structural rearrangement of the anisole–water cluster with in the complex with respect to the isolated phenol [4]. Also electronic excitation and on the possible presence of a sec- the hydrogen-bond distance decreases in the excited state ond relevant interaction point between the oxygen atom of water and the aromatic hydrogen atom in ortho position of anisole. Different results were reported for adenine–H O * Corresponding author. Address: Dipartimento di Chimica, Universita` 2 di Firenze, Firenze, Italy. Fax: +39 055 4572 451. [9,10]. The adenine–H2O complex was clearly observed E-mail address: maurizio.becucci@unifi.it (M. Becucci). with high energy excitation (i.e., photons below 200 nm 0301-0104/$ - see front matter Ó 2006 Elsevier B.V. All rights reserved. doi:10.1016/j.chemphys.2006.08.004 G. Piani et al. / Chemical Physics 330 (2006) 138–145 139 wavelength or direct ionization by electronic impact). If the interval between 0 °C and 25 °C. Mass spectra were adenine–H2O complex is excited to the S1 excited state, obtained via multi-photon ionization with different photon then the corresponding cation is observed only if a probe energy, in-resonance and out-of-resonance for the aniline– pulse (used for ionization) is provided with a delay not water complex. The same procedures were applied for the longer than 220 fs with respect to the pump pulse. The study of the aniline–methanol complex. structure of the adenine–H2O 1:1 complex has not been determined by experiments but different models for this 2.2. Ab initio methods system have been reported [11,12]. In some of these models, water is connected to a hydrogen atom of the amino group In order to evaluate the properties of the aniline–H2O and one of the aromatic N atoms [11]. complex in the excited state, we have followed the guide- In this respect, it seems quite interesting to investigate lines provided by Fang for a similar study on phenol– the properties of the simplest aromatic amino molecule, H2O [20]. The equilibrium structure and the interaction i.e., aniline and the complex it forms with water. Our aim energy of the aniline–H2O complex have been calculated is to contribute, with experimental data and quantum cal- by second-order Møller–Plesset (MP2) perturbation theory culation, to the description of the changes in the properties and complete active space-self consistent field (CASSCF) of clusters with electronic excitation. methods in the ground electronic state, S0, and by single It has been shown by microwave spectroscopy experi- configuration interaction (CIS) and CASSCF methods in ments [17] that, in the ground state, aniline acts as a base the first excited electronic state, S1. In order to account with water placed in its symmetry plane above the aromatic for the correlation energy, the CASSCF calculations were ring, connected to the amino group via hydrogen bonding, followed by single point CASPT2 energy calculations. the hydrogens of the amino group being on the opposite The cc-pvdz basis set has been employed in all calculations side of water. The properties of aniline in the gas phase as suggested by previous reports [21,22]. We also used an have been studied in detail both in the ground and the first augmented (aug-cc-pvdz) basis set in order to know its excited electronic state by rotationally resolved experi- effect on the results. The CASSCF active space includes ments [13–15]. Very recently, photon-induced dissociation all p electrons and p orbitals of the aromatic ring (three of anionic clusters containing aniline has been reported. p bonds, three corresponding antibonding orbitals) and There, the electron photo-detachment process have been the nitrogen n lone pair of aniline. This results in an active studied for negative ionic clusters formed by iodide with space of eight electrons in seven orbitals and is denoted by aniline [16]. By the measure in coincidence of the detached CAS(8,7). The oxygen lone pair orbitals of water were not electron and the neutral particles, it has been demonstrated included in the active space due to the difference in the that the cluster is dissociating with quantum yield almost orbital energies from those of p orbitals, which are near- unitary after the electron removal. degenerate. In the case of phenol–H2O complex [20],it We report here on the measure, by resonance-enhanced has been shown that the CASSCF convergence is seriously multi-photon ionization spectroscopy (REMPI), of the degraded when the n orbitals of water were included. The S1 S0 electronic transition of aniline–H2O and the clo- interaction energy derived from this type of calculation is sely related aniline–methanol complex, and on quantum subject to the basis set superposition error (BSSE) that calculations aiming at the description of the system in both can be corrected using the counterpoise method of Boys the ground and the excited. and Bernardi [23]. Therefore, the corrected interaction energy is calculated as: 2. Experimental and computational methods AB AB AB Eint ¼ EABðABÞ À EABðAÞ À EABðBÞ Z 2.1. Experimental methods where we define EY(X) as the energy of a molecular sys- tem X at the equilibrium geometry of the molecular system We have made a search for the S1 S0 electronic tran- Y with the set of basis functions related to the molecular sition of the aniline–H2O complex by REMPI spectroscopy system Z. A better evaluation of the binding energy in experiments in both 2 photon-1 colour and 2 photon-2 col- the complex, called stabilization energy, can be obtained our excitation schemes. The laser spectrometer coupled to a introducing the fragment relaxation in the counterpoise time-of-flight mass spectrometer was already described in scheme according to the expression: detail elsewhere [5]. The molecular beam was prepared by E ¼ E þ E ðAÞA þ E ðBÞB À E ðAÞA À E ðBÞB: flowing an aniline–helium gas mixture through a pulsed stab int AB AB A B valve (500 lm diameter). The stagnation pressure was The first term is the corrected interaction energy and the fol- 300 KPa. Aniline was placed in a temperature controlled lowing four terms represent the relaxation contribution, compartment and its partial pressure regulated controlling which compensates for the geometry distortion of the sub- A B its temperature (in a range between À10 °C and 30 °C). In system in the supermolecule, EAB(A) and EAB(B) , with re- A B order to produce aniline–water complexes, the helium was gard to the isolated optimum geometry, EA(A) and EB(B) flowing also through another external compartment con- [24]. Therefore, seven energy calculation had to be carried taining liquid water held at a temperature ranging in an out, instead of the three needed for the determination of 140 G.
Load more

Recommended publications
  • Mdi), 1,6 Hexamethylene Diisocyanate (Hdi
    4.03.11. PRODUCTION OF ISOCYANATES FOR POLYURETHANE PRO- DUCTION CHEMICALS AND ALLIED APPLICATION NOTE 4.03.11 PRODUCTION OF ISOCYANATES FOR POLYURETHANE PRODUCTION METHYLENE DIPHENYL DIISOCYANATE (MDI), 1,6 HEXAMETHYLENE DIISOCYANATE (HDI) Typical end products Polyurethane foam for different applications, for example, bedding, of materials can be produced to meet the needs for furniture, packaging, coatings and elastomers. specific applications. Chemical curve: R.I. for MDI at Ref. Temp. of 25˚C Application The most commonly used isocyanates for the production of PU are methylene diphenyl diisocyanate (MDI) and toluene diisocyanate (TDI). If color and transparency are important, an aliphatic diisocyanate such as hexamethylene diisocyanate (HDI) is used. The first step in the production of polyurethane is the synthesis of the raw materials. The diisocyanate is typically produced from basic raw materials via nitration, hydrogenation and phosgenation. The feedstock and initial processing steps depend on the Introduction desired isocyanate, but all go through a phosgenation step. Polyurethanes (PUs) are a class of versatile materials with great potential for use in different applications. For instance, for the production of MDI, benzene and They are used in the manufacture of many different nitric acid are reacted to produce nitrobenzene. After items, such as paints, liquid coatings, elastomers, a hydrogeneration step, the nitrobenzene is converted insulators, elastics, foams and integral skins. to aniline. It is then condensed with formaldehyde to produce methylene diphenyl diamine (MDA), the Polyurethanes are produced by polymerization of precursor for MDI. The MDA is fed to a phosgenation a diisocyanate with a polyol. Because a variety of reactor where it reacts with phosgene to produce the diisocyanates and a wide range of polyols can be end-product MDI.
    [Show full text]
  • MDI Process Update Process Economics Program Review 2016-13
    ` IHS CHEMICAL MDI Process Update Process Economics Program Review 2016-13 March 2017 ihs.com PEP Review 2016-13 MDI Process Update Ron Smith Senior Principal Analyst Downloaded 20 March 2017 08:28 AM UTC by Anandpadman Vijayakumar, IHS ([email protected]) IHS Chemical | PEP Review 2016-13 MDI Process Update PEP Review 2016-13 MDI Process Update Ron Smith, Senior Principal Analyst Abstract Isocyanates are a major ingredient for the production of polyurethane products that are formed by the reactive polymerization of isocyanates with polyols. A long and difficult search for a reasonable economic pathway to produce isocyanates by vapor-phase phosgenation of diphenylmethane diamine (MDA) in place of liquid-phase phosgenation of MDA has been developed and commercialized since our last report on isocyanates (PEP Report 1E) was published in August 1992. In this review, we investigate large-scale, single-train integrated technology and economics for the production of methylene diphenyl diisocyanate (MDI), including condensation of aniline with formaldehyde to produce MDA, production of phosgene from carbon monoxide and chlorine, gas-phase phosgenation of MDA to produce crude MDI, and separation/recovery of MDI products. The key gas-phase phosgenation step produces isocyanates from MDA at high pressure and temperature, enabling a significant shortening of residence time in the reactor. The rate determining step is the dissociation of the polymeric MDA–carbonyl chloride intermediate into polymeric MDI and HCl followed by HCl removal. A summary of the process economics for the production of 373 million lbs/yr of crude MDI and 336 million lbs/yr of polymeric MDI (PMDI) and 37 million lbs/yr of pure MDI for continuous vapor-phase isocyanate production shows that on a US Gulf Coast basis, the world-scale, single-train, integrated vapor-phase technology–based plant will meet plant gate costs.
    [Show full text]
  • Reactions of Aromatic Compounds Just Like an Alkene, Benzene Has Clouds of  Electrons Above and Below Its Sigma Bond Framework
    Reactions of Aromatic Compounds Just like an alkene, benzene has clouds of electrons above and below its sigma bond framework. Although the electrons are in a stable aromatic system, they are still available for reaction with strong electrophiles. This generates a carbocation which is resonance stabilized (but not aromatic). This cation is called a sigma complex because the electrophile is joined to the benzene ring through a new sigma bond. The sigma complex (also called an arenium ion) is not aromatic since it contains an sp3 carbon (which disrupts the required loop of p orbitals). Ch17 Reactions of Aromatic Compounds (landscape).docx Page1 The loss of aromaticity required to form the sigma complex explains the highly endothermic nature of the first step. (That is why we require strong electrophiles for reaction). The sigma complex wishes to regain its aromaticity, and it may do so by either a reversal of the first step (i.e. regenerate the starting material) or by loss of the proton on the sp3 carbon (leading to a substitution product). When a reaction proceeds this way, it is electrophilic aromatic substitution. There are a wide variety of electrophiles that can be introduced into a benzene ring in this way, and so electrophilic aromatic substitution is a very important method for the synthesis of substituted aromatic compounds. Ch17 Reactions of Aromatic Compounds (landscape).docx Page2 Bromination of Benzene Bromination follows the same general mechanism for the electrophilic aromatic substitution (EAS). Bromine itself is not electrophilic enough to react with benzene. But the addition of a strong Lewis acid (electron pair acceptor), such as FeBr3, catalyses the reaction, and leads to the substitution product.
    [Show full text]
  • Catalytic Dry Oxidation of Aniline, Benzene, and Pyridine Adsorbed on a Cuo Doped Activated Carbon
    Korean J. Chem. Eng., 26(3), 913-918 (2009) SHORT COMMUNICATION Catalytic dry oxidation of aniline, benzene, and pyridine adsorbed on a CuO doped activated carbon Bingzheng Li*,**, Zhenyu Liu*,***,†, Zhiping Lei*,****, and Zhanggen Huang* *State Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan 030001, P. R. China **Graduate University of Chinese Academy of Sciences, Beijing 100049, P. R. China ***State Key Laboratory of Chemical Resource Engineering, Beijing University of Chemical Technology, Beijing 100029, P. R. China ****School of Chemical & Chemistry, Anhui university of Technology, Maanshan, 243002, P. R. China (Received 31 July 2008 • accepted 27 December 2008) Abstract−Adsorption of aniline, benzene and pyridine from water on a copper oxide doped activated carbon (CuO/ AC) at 30 oC and oxidation behavior of the adsorbed pollutants over CuO/AC in a temperature range up to 500 oC are investigated in TG and tubular-reactor/MS systems. Results show that the AC has little activity towards oxidation of o the pollutants and CuO is the active oxidation site. Oxidation of aniline occurs at 231-349 C and yields mainly CO2, o H2O and N2. Oxidation of pyridine occurs at a narrower temperature range, 255-309 C, after a significant amount of desorption starting at 150 oC. Benzene desorbs at temperatures as low as 105 oC and shows no sign of oxidation. The result suggests that adsorption-catalytic dry oxidation is suitable only for the strongly adsorbed pollutants. Oxidation temperatures of CuO/AC for organic pollutants are higher than 200 oC and pollutants desorbing easily at tempera- tures below 200 oC cannot be treated by the method.
    [Show full text]
  • The Dissociation Constants of Some Disubstituted Anilines and Phenols in Aqueous Solution at 25°C
    JOURNAL OF RESEARCH of th e National Bureau of Standards - A. Physics and Chemistry Vol. 71A, No.3, May- June 1967 The Dissociation Constants of Some Disubstituted Anilines and Phenols in Aqueous Solution at 25°C R. A. Robinson Institute for Materials Research, National Bureau of Standards, Washington, D.C. 20234 (February 21, 1967) The dissociati on constants of s ix di s ubstituted anilines and of fiv e dis ubstituted phenols in aqueous solution a t 25 °C have been measured u sing th e s pectrophotometric method. Consideration is give n to the ex tent to whi c h these di ssociation co nstants can be predicted from corresponding values for monosubs tituted anilines and Dh enols. In addition, the question as to wh eth er the pK value of a sub· stituted anil ine can be predicted from the pK value of a phenol with substituents in the same positions is also investigated. ~ Key Word s: Di ssociation cons tant, subs tituted a nilines, substituted phenols. 1. Introduction OR), Cl, and it is not surprising that there should be steric e ffects whi ch inte rfe re with the additivity In an earlier paper [l]i the results of measurements relation. of the pK values of the six di chloroanilines and the Secondly, it was found that a linear relationship six dichlorophenols in aqueous solution at 25°C have existed between the pK value of a di chloroaniline, been reported. The conclusions drawn from this pKA , and the pK value of the corresponding di chloro­ I work can be summarized brie fl y in two statements.
    [Show full text]
  • Toluene Solvent
    Issued: Data Sheet 23-Jul-2009 Product Name Toluene S Product Code T1402 Africa Product Category Aromatics CAS Registry Number 108-88-3 EINECS Number 203-625-9 Typical Properties Property Unit Method Value Density @15°C kg/l ASTM D4052 0.871 Density @20°C kg/l ASTM D4052 0.867 Cubic Expansion Coefficient @20°C (10^-4)/°C - 11 Refractive Index @20°C - ASTM D1218 1.497 Color Saybolt ASTM D156 +30 Acid Wash Color - ASTM D848 1 Distillation, IBP °C ASTM D86 110 Distillation, DP °C ASTM D86 111 Relative Evaporation Rate (nBuAc=1) - ASTM D3539 1.9 Antoine Constant A # kPa, °C - 6.07577 Antoine Constant B # kPa, °C - 1342.31 Antoine Constant C # kPa, °C - 219.187 Antoine Constants: Temperature range °C - +40 to 100 Vapor Pressure @0°C kPa Calculated 0.89 Vapor Pressure @20°C kPa Calculated 2.9 Saturated Vapor Concentration @20°C g/m³ Calculated 110 Aromatics %v/v GC > 99 Benzene %v/v GC < 0.04 Non-Aromatic Hydrocarbons %v/v GC < 1 Flash Point °C IP 170 4 Auto Ignition Temperature °C ASTM E659 535 Explosion Limit: Lower %v/v - 1.2 Explosion Limit: Upper %v/v - 7.1 Electrical Conductivity @20°C pS/m - < 10 Aniline Point, Mixed °C ASTM D611 9 Kauri-Butanol Value - ASTM D1133 105 Pour Point °C ASTM D97 < -50 Surface Tension @20°C mN/m Du Nouy ring 29 Viscosity @25°C mm²/s ASTM D445 0.64 Hildebrand Solubility Parameter (cal/cm³)^½ - 8.9 Hydrogen Bonding Index - - 4.2 Fractional Polarity - - 0.001 Molecular Weight g/mol Calculated 92 (#) In the Antoine temperature range, the vapor pressure P (kPa) at temperature T (°C) can be calculated by means of the Antoine equation: log P = A - B/(T+C) Test Methods Copies of copyrighted test methods can be obtained from the issuing organisations: American Society for Testing and Materials (ASTM) : www.astm.org Energy Institute (IP) : www.energyinst.org.uk For routine quality control analyses, local test methods may be applied that are different from those mentioned in this datasheet.
    [Show full text]
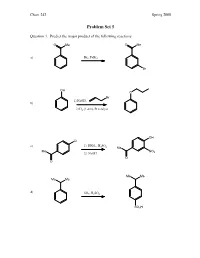
  • Problem Set 5
    Chem 242 Spring 2008 Problem Set 5 Question 1. Predict the major product of the following reactions. O Me O Me a) Br2, FeBr3 Br OH O Br 1) NaOH, b) 2) H2 (1 atm), Pt catalyst OH Cl c) 1) HNO , H SO 3 2 4 Me Me NO 2) NaOH 2 O O Me Me Me Me d) SO3, H2SO4 SO3H Chem 242 Spring 2008 Question 2. Provide reagents that will accomplish the following transformations. Multiple steps may be needed. 1) acetyl chloride, AlCl a) 3 H3C 2) SO3/H2SO4 SO3H O NH2 NO2 Br Br 1) H2 (1 atm), Pd catalyst b) 2) Br2 (no FeCl3 needed) Br Me Me O Me 1) isobutyryl chloride, AlCl3 c) 2) Cl2, FeCl3 Cl Me Me Me Me OH 1) NaOH, Et–I d) 2) t-butyl chloride, AlCl3 OEt Chem 242 Spring 2008 Question 3. A student wanted to synthesize para-nitroaniline by nitration of aniline as shown below. NH2 NH2 HNO3, H2SO4 + some ortho-product NO2 a) Provide a mechanism for the formation of para-nitroaniline. O O O H2SO4 N N N O OH O OH2 O NH NH NH NH NH2 2 2 2 2 O N O2N H O2N H O2N H O2N H O NH2 HSO4 NO2 b) When the experiment was actually attempted, the reaction was very sluggish and the product mixture contained large amounts of meta-nitroaniline. Briefly explain the sluggish rate and the formation of meta-nitroaniline. + In strong acid, the amine will become protonated. An –NH3 group is stongly deactivating and meta-directing.
    [Show full text]
  • Molecular Interactions of Aniline in Toluene + Iso-Butanol System
    Indian Journal of Pure & Applied Physics Vol. 49, December 2011, pp. 803-808 Molecular interactions of aniline in toluene + iso-butanol system G Mahendran & L Palaniappan* Department of Physics, Arignar Anna Government Arts College, Namakkal, Tamil Nadu, India *Department of Physics (DDE), Annamalai University, Annamalainagar 608 002, Tamil Nadu, India *E-mail: [email protected] Received8 February2011; revised 2 September 2011; accepted 17 October 2011 The separation efficiency of aniline by destructing the azeotropic formation in the binary toluene + iso-butanol has been analysed using ultrasonic techniques. Ultrasonic velocity, density and viscosity values have been measured at 303 K in the ternary system of aniline + toluene + iso-butanol and thermo dynamical approach is applied to evaluate the molar volume, adiabatic compressibility, internal pressure, molar cohesive energy and their excess values. Results are interpreted in terms of molecular interactions between the components of the mixtures and compared with molecular interaction parameter that can highlight the role of aniline in the azeotropic destruction of the chosen binary. Observed excess values lend further support to the interactions found in the binary and ternary systems. The dipole type interaction existing between aniline and iso-butanol is found to be the predominant factor for destructing the azeotrope formation. Keywords: Azeotropes, Binary mixtures, Ternary mixtures, Velocity, Density, Molecular interactions 1 Introduction ultrasonic techniques. As alcohols are invariably Velocity of sound waves in a medium is found as a component in petrochemical azeotropes, fundamentally related to the binding forces between iso -butanol is chosen for the present study. Toluene is the atoms or the molecules. The variations of taken as second azeotropic component because of its ultrasonic velocity and related parameters throw some importance in the separation process of petrochemical light on the intermolecular interactions and the intermediates.
    [Show full text]
  • Dissociation Constants of Organic Acids and Bases
    DISSOCIATION CONSTANTS OF ORGANIC ACIDS AND BASES This table lists the dissociation (ionization) constants of over pKa + pKb = pKwater = 14.00 (at 25°C) 1070 organic acids, bases, and amphoteric compounds. All data apply to dilute aqueous solutions and are presented as values of Compounds are listed by molecular formula in Hill order. pKa, which is defined as the negative of the logarithm of the equi- librium constant K for the reaction a References HA H+ + A- 1. Perrin, D. D., Dissociation Constants of Organic Bases in Aqueous i.e., Solution, Butterworths, London, 1965; Supplement, 1972. 2. Serjeant, E. P., and Dempsey, B., Ionization Constants of Organic Acids + - Ka = [H ][A ]/[HA] in Aqueous Solution, Pergamon, Oxford, 1979. 3. Albert, A., “Ionization Constants of Heterocyclic Substances”, in where [H+], etc. represent the concentrations of the respective Katritzky, A. R., Ed., Physical Methods in Heterocyclic Chemistry, - species in mol/L. It follows that pKa = pH + log[HA] – log[A ], so Academic Press, New York, 1963. 4. Sober, H.A., Ed., CRC Handbook of Biochemistry, CRC Press, Boca that a solution with 50% dissociation has pH equal to the pKa of the acid. Raton, FL, 1968. 5. Perrin, D. D., Dempsey, B., and Serjeant, E. P., pK Prediction for Data for bases are presented as pK values for the conjugate acid, a a Organic Acids and Bases, Chapman and Hall, London, 1981. i.e., for the reaction 6. Albert, A., and Serjeant, E. P., The Determination of Ionization + + Constants, Third Edition, Chapman and Hall, London, 1984. BH H + B 7. Budavari, S., Ed., The Merck Index, Twelth Edition, Merck & Co., Whitehouse Station, NJ, 1996.
    [Show full text]
  • Electrical and Optical Properties of Poly(Aniline-Co-8-Anilino-1-Napthalene Sulphonic Acid) — a Material for ESD Applications
    CORE Metadata, citation and similar papers at core.ac.uk Provided by IR@NPL Indian Journal of Pure & Applied Physics Vol. 47, September 2009, pp. 667-675 Electrical and optical properties of poly(aniline-co-8-anilino-1-napthalene sulphonic acid) — A material for ESD applications Vineet Bansal 1,2 , Hema Bhandari 1, M C Bansal 2 & S K Dhawan 1* 1Polymeric & Soft Materials Section, National Physical Laboratory, Dr K S Krishnan Road, New Delhi 110 012 2Department of Physics, M M H College, Ghaziabad 201 009 *E-mail: [email protected] Received 22 January 2009; accepted 12 June 2009 The homopolymer of aniline (An) and its copolymer with 8-anilino-1-napthalene suplhonic acid (8-ANSA) was synthesized by chemical oxidative as well as electrochemical polymerization process in the presence of para -toluene sulphonic acid (PTSA) as a dopant. The spectral, thermal, morphological and electrochemical properties of PTSA doped polyaniline and its copolymer (An-co-8-ANSA) were studied and compared to elucidate the effect of the inclusion of 8-ANSA in the copolymer feed. The resultant copolymer showed better solubility and processibility but this approach usually results in the lowering of conductivity, hence the ratio of aniline and 8-ANSA in the copolymer feed was selected to 80:20. The room temperature conductivity of the PTSA doped polyaniline (PANI-PTS) and poly(An-co-8-ANSA) in 80:20 was found to be in the order of 1.74 S/cm to 9.77×10 −1 S/cm, respectively. Conductivity mechanism of charge transport has been investigated in the range 30-300K.
    [Show full text]
  • CH 2280 Synthesis and Nitration of Acetanilide
    CH 2280 Synthesis and Nitration of Acetanilide Materials From the Chemicals Hood: From the Stockroom (Blue Bin): Week 1: Week 1: Acetic anhydride ½” pea-sized stirbar Aniline Stirbar retriever Week 2: Week 2: Glacial acetic acid 1” stirbar Concentrated sulfuric acid Stirbar retriever 50/50 Nitric acid/ sulfuric acid solution Ethanol Sodium bicarbonate aqueous solution (squirtbottle) 9 cm large Buchner funnel This is another two-step experiment and takes two weeks. The first step is acetylation of aniline to form acetanilide. This is done the first week. The second step is nitration of acetanilide. You will do that reaction the second week. You will determine which isomer of nitroacetanilide you formed using melting point, infrared, and NMR spectroscopy. Procedure – Preparation of Acetanilide Place an ice bath on top of the stir plate in the hood. In the ice bath place a 50-mL Erlenmeyer flask containing 10 mL of acetic anhydride and a magnetic stir bar. Turn the stirring on but keep the heat OFF. Add 10 mL of aniline (CAUTION: see Safety Note 1) 1 mL at a time over 10 minutes. Pour the reaction mixture into a beaker containing a 100 mL of cold water. If a solid does not form immediately, scratch the walls of the beaker with a glass rod for a few minutes. Vacuum filter the crystals and allow them to dry until the next lab period. At that time, determine the melting point, IR, and NMR of the product. 1 Procedure – Nitration of Acetanilide Place 6.5 g of acetanilide in a 125-mL Erlenmeyer flask, add 10 mL of glacial acetic acid (CAUTION: strong irritant), and warm the flask on a steam bath until the acetanilide dissolves.
    [Show full text]
  • Studies in Nitration, 111. Nitration of Aniline and of Certain of Its N-Alkyl, A;-Aryl and N-Acyl Derivatives
    STUDIES IN NITRATION. I395 STUDIES IN NITRATION, 111. NITRATION OF ANILINE AND OF CERTAIN OF ITS N-ALKYL, A;-ARYL AND N-ACYL DERIVATIVES. BY J. BISHOP TINGLEAND F. C. BLANCK. Received June 16,rgo8. Theoretical. The fact that aniline cannot be directly nitrated and that, under ordi- nary conditions, nitric acid converts it into tarry matter, is usually ac- counted for by stating that the acid attacks the amino group more read- ily than the benzene nucleus.2 Such an explanation cannot be accepted unreservedly, not only because it is devoid of experimental foundation, but also because of certain theoretical objections which may be urged against it. Among the latter may br mentioned the view, held by manv chemists, that “substitution” in the nucleus is really preceded by addi- tion or substitution in the side chain if one be present, or, addition in the nucleus itself, followed in each case by subsequent rearrangement. Further, the fact that, in general, the aromatic amine ni~ratcsare usually stable, whereas, the nitrites are either highly unstable or altogether in. capable of isolation suggests that nitrous acid may really be the ac.tive cause of the unfavorable result of direct nitration experiments. This view gains support from the well-known observations made in carrying out the diazo reaction; some resinous matter is always formed. and it is apt. to be the chief; or even the only tangible product of the experiment, unless the conditions are adjusted specially for each individual amine. In view of these considerations, it appeared to us that it would be worth while to reinvestigate the direct nitration of aniline, employing conditions which should exclude nitrous acid as completely as possible from the ma- terials employed, provision being also made for the speedy destruction or removal of any of this acid which might be formed during the course of the experiments.
    [Show full text]