DOCSLIB.ORG

J O U R N a L O F P U R E a N D a P P L I

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
J O U R N a L O F P U R E a N D a P P L I ISSN 0256-4637 VOLUME 31 NUMBER 1 January-March, 2009 J o u r n a l o f P u r e a n d A p p l i e d Ultrasound techniques for characterizing liquids 1 I. broad-band spectrometers — UDO KAATZE Ultrasound techniques for characterizing liquids. 13 II. survey of single frequency methods — UDO KAATZE Ultrasonic internal rotary inspection system (IRIS) for heat 24 exchanger and steam generator tubes — A. JOSEPH, GOVIND K. SHARMA and T. JAYAKUMAR Nondestructive characterization of a lyotropic liquid crystalline system 31 — GIRIDHAR MISHRA, R.R. YADAV and S.K. KOR Report - NSU-XVII 36 Dr. T.K. Saksena - A Profile 38 Information for Authors 40 SOC S IET IC Y N O O F S A I N R D T I A L Website : www.ultrasonicsindia.com U Fo 4 u 97 nded 1 A Publication of — Ultrasonics Society of India A Quarterly Publication of Ultrasonics Society of India SOC S IET IC Y N J o u r n a l o f P u r e a n d A p p l i e d O O F S A I N R D T I A L U F ou 74 nded 19 Ultrasonics Society of India No. 1 Volume 31 Jan.-March, 2009 Ultrasonics Society of India established in 1974, is engaged in the promotion of research and diffusion of Chief Editor Dr. S.K. Jain knowledge concerning the field of ultrasonics and e-mail : [email protected] allied areas. Editorial Board Patrons : Dr. A. R. Verma Prof. S.S. Mathur Ex. Professor, Indian Institute of Technology, Dr. V. N. Bindal New Delhi Prof. E.S.R. Gopal Prof. V.P. Bhatnagar Ex. Professor, Delhi College of Engineering, Executive Board : New Delhi President Dr. Krishan Lal Mr. A.D. Prasad Ex. Chief Engineer, IDPL, Noida (U.P.) Vice Presidents Dr. Janardan Singh Dr. Klaus Beissner Physikalisch Technische- Bundesanstalt, Dr. P. Palanichamy Germany General Secretary Mr. S.K. Singhal Dr. J.N. Som Ex. Scientist, National Physical Laboratory, Treasurer Mr. G.K. Kohli New Delhi Publication Secretary Dr. Mukesh Chandra Publication Committee Joint Secretary Mr. N.K. Sharma Members Mr. Subhash Chandra Dr. Sanjay Yadav National Physical Laboratory, New Delhi Dr. J.N. Som Dr. A.K. Nain Dayal Singh College, New Delhi Dr. S.K. Shrivastava Mr. Subhash Chandra Ex. Technical Officer Mr. V.K. Ojha National Physical Laboratory, New Delhi Co-opted Members Dr. Raja Ram Yadav Mr. Gurmukh Singh Scientist F Mr. S.C. Dhawan E.R.T.L. (North), New Delhi SUBSCRIPTION (postage paid) Membership of the Society is open to individuals without distinction of sex, race or nationality and to Single Rs. 550/- US $ 50/- Annual Rs. 2200/- US $ 200/- bodies who subscribe to the aims and objectives of the USI Member Free Society. The membership fee is as follows : ADVERTISEMENT The Journal offers opportunity of wide and effective publicity for the Class of Membership Subscription manufacturers, suppliers of ultrasonic equipment, device and materials (one time) and also for other scientific instruments and components. Tariff is as follows : Honorary Fellow Nil Back Cover Rs. 2500/- US $ 100/- Fellow/Member Rs. 1200/- Inside Cover Rs. 1500/- US $ 75/- Associate Member Rs. 500/- Full Page Rs. 1000/- US $ 50/- (for 5 yrs.) Half Page Rs. 600/- US $ 30/- Corporate Member Rs. 6000/- Fellow/Member (Foreign) US $ 100/- Discount of 20% is admissible for 4 successive insertions. Corporate Member (Foreign) US $ 500/- Membership forms and the relevant information can The submission of papers and all other correspondence regarding the be downloaded from the website or obtained from : Journal may please be addressed to : Publication Secretary The General Secretary Journal of Pure and Applied Ultrasonics Ultrasonics Society of India C/o Ultrasonics Society of India National Physical Laboratory National Physical Laboratory Dr. K. S. Krishnan Marg Dr. K. S. Krishnan Marg New Delhi-110012 New Delhi-110012 e-mail : [email protected] J. Pure Appl. Ultrason. 31 (2009) pp. 1-12 Ultrasound techniques for characterizing liquids I. broad-band spectrometers† UDO KAATZE Drittes Physikalisches Institut, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany e-mail : [email protected] This tutorial gives a short introduction into the broad-band ultrasonic spectroscopy of liquids. The fundamentals of acoustical methods are summarized. Preference is given to methods using continuous waves and pulse modulated signals. Related techniques, such as time-domain methods with step-like excitation of the sample and with optical monitoring of acoustical waves (Brillouin scattering), are briefly mentioned, too. Constructions of some types of sonic cells for liquids and electronic set-ups for spectral measurements are presented in detail. The merits and limitations of different techniques of measurements, covering the frequency range from almost 10 kHz up to nearly 10 GHz, are discussed. Together with applications in the relaxation properties of liquids, examples of broadband ultrasonic spectra are shown. Key words : Ultrasonic spectroscopy, liquids, relaxations, acoustical absorption coefficient, sound velocity INTRODUCTION The retarded energy transfer between different molecular states of a liquid results in a phase Acoustical signals couple to liquids via lag between pressure and density of a harmonic fundamental parameters, such as the density, acoustic wave. Therefore, acoustic energy is viscosity, and heat capacity1-11. By utilizing these absorbed and dissipated as heat. According to parameters acoustical measurements probe the the fluctuation - dissipation theorem and, by native systems; labels or markers, as required by analogy with the Kramers - Kronig relations12,13, many other measurement techniques for liquids, a characteristic velocity dispersion dc/dν > 0 is are not necessary. Variations in the relevant related with the absorption (c is the sound velocity liquid parameters may result from variations of the liquid). In a relaxing system the relative in the thermodynamic parameters, for example dispersion step [c(ν→0)-c(ν→∞)]/c(ν→∞) is small from changes in the hydrodynamic pressure, the and frequently does not exceed the experimental temperature, or the pH. Variations in the sample property following thereby are often investigated by single-frequency methods which will be the focus of part II of this review. Density, viscosity, and heat capacity of a liquid may also vary with the frequency ν of the sonic field. Such variations happen when an energy barrier exists that prevents molecules, ions, or mesoscopic structures of a liquid from instantaneously following the external field. Fig.1. Sound velocity spectrum of a 0.4 mol/l solution 14 of zinc chloride (ZnCl2) in water at 25°C. The †Invited talk presented at NSU-XVII, B.H.U., Varanasi, line shows the dispersion as calculated from the Dec. 4-6, 2008. J. Pure Appl. Ultrason. Vol. 31 No. 1 (2009) associated absorption spectra 1 errors. Fig. 1 displays already an extraordinarily large dispersion for aqueous systems. Because of the small dispersion amplitude of most liquid relaxations only a comparatively few broad- band sound velocity spectra exist presently. Outstanding exceptions are given, for instance 15 and 16. Because of the typically small dispersion, this part of the review is mainly restricted to ultrasonic absorption measurements. If small effects of thermal conductivity, which play a noticeable role only in liquid metals, are neglected, the laws of conservation of mass and momentum yield the following relation for the complex propagation constant γ =α+iβ of a 1 sinusoidal acoustic wave within a liquid Fig.2. Ultrasonic absorption spectra of a 0.5 mol/l solution of copper chloride (CuCl2) in water at 25°C14 Experimental total absorption-per-wavelength data are shown by points, the asymptotic high-frequency background absorption is represented by the dashed line, and the excess absorption-per-wavelength is (1) indicated by circles. The full line is the graph of a Debye-type relaxation term eq. 8 with the following 2 Here i =-1, α is the absorption coefficient, β = 2π/γ value for the parameters: A = 7. 6·10-3, τ = 0.35 ns where γ = c/ν is the wavelength, ω = 2πν is the angular frequency, ρ is the density, (6) (2) can be separated into two parts. Here is the adiabatic compressibility of the liquid, and ηs and ην are the shear and volume viscosity, respectively. The latter is related to the curl-free (7) part of the acoustic field. At small frequencies -1 is independent of ν if the compressibility does (ω«[κs(4ηs/3+ην] ) follows for the absorption along a wavelength not depend on ν. It is obvious from eq.(1) that a frequency dependent shear viscosity or volume viscosity leads also to a frequency dependent β and thus a frequency dependent cs. As, however, (3) briefly discussed above, the dispersion in the sound velocity of liquids is normally small. Strictly, κS with η and η referring to very low frequencies. s0 ν0 must be replaced by κS∞ in eq. (7). Because of molecular interactions, indicated by the internal energy barriers mentioned before, both Normally, in liquid spectroscopy we are the shear viscosity and the volume viscosity may interested in the excess absorption-per-wavelength be subject to relaxation and may thus depend on (αλ)exc(ν) only. Nevertheless the asymptotic high- frequency. If we write frequency term Bν in eq. (6) acts a considerable influence on the measurements. Due to its frequency ν (4) dependence, proportional to , it dominates the total absorption-per-wavelength αλ at high frequencies and and restricts measurements of liquids to frequencies below some GHz. An illustrative example, in which (αλ)exc ≈ 0.1·(αλ) only at 1 GHz, is given in Fig. 2. (5) It is the asymptotic high-frequency ("background") term Bν which necessitates different methods of with η = η (ν→∞) and η = η (ν→∞) denoting s∞ s ν∞ ν measurements at low and high frequencies.
Load more

Recommended publications
  • LLB(Hons)Isem 2018.Xlsx
    Roll No Enrol No Name Father;s Name Mother's NamM1 M2 M3 M4 M5 M6 M7 Total Result Unit 1812201 D1771001 ABDUL BASIT JALEEL AHMAD DURDANA S 49 51 57 54 54 55 53 373 Pass ADC 1812202 D1771002 ABHAY PRATAP CHHOTE LAL GUPTA CHANDRA K AA AA AA AA AA AA AA Abs Absent ADC 1812203 D1771003 ABHISHEK AWASTHI ANIL KUMAR AWASTHI ANJU AWAS 56 66 60 57 64 59 61 423 Pass ADC 1812204 D1771004 ABHISHEK DWIVEDI SHASHI DHAR DWIVEDI SHUSILA DE 49 30 57 47 52 56 59 350 Elig.for SE ADC 1812205 D1771005 ABHISHEK JAYSAVAL RAJESH KUMAR JAYSAVAL NEELAM JAY45 56 56 54 52 60 56 379 Pass ADC 1812206 10AU/1920 ABHISHEK KUMAR YADAV CHANNI PRASAD YADAV SUMAN YAD 47 49 55 47 61 53 53 365 Pass ADC 1812207 D1771006 ABHISHEK KUMAR YADAV RAM KARAN YADAV RAJ KUMAR 46 54 56 56 56 61 56 385 Pass ADC 1812208 D1771007 ABHISHEK PANDEY HARIKESH PANDEY INDRA PAND44 54 55 61 62 58 58 392 Pass ADC 1812209 D1771008 ABHISHEK PANDEY UMA SHANKAR PANDEY ASHA DEVI P43 42 56 42 50 45 55 333 Pass ADC 1812210 U1322166 ABHISHEK SHANKER TIWARI ANIL KUMAR TIWARI RITA TIWAR 57 66 62 63 59 65 54 426 Pass ADC 1812211 D1771009 ABHISHEK TIWARI JAGADAMBA PRASAD TIWARI KAMLESH TI 56 60 62 50 44 54 55 381 Pass ADC 1812212 D1771010 ABHISHEK YADAV HARIBANSH YADAV LALTI DEVI 52 57 55 51 53 54 54 376 Pass ADC 1812213 D1771011 ABID KHAN ABDUL QAYUUM SHAHIDA KHUF --- --- --- --- --- --- UFM UFM ADC 1812214 16AU/1051 ABRAR ALI LIYAKAT ALI BADRUN NIS47 55 55 35 53 46 56 347 Pass ADC 1812215 S1420006 ADITI BISARYA SAURABH BISARYA SUDHA BISA57 60 58 53 51 53 59 391 Pass ADC 1812216 D1120029 ADITYA NARAYAN TIWARI
    [Show full text]
  • List Officers-M&E Dept for Exam-13.03.16
    KOLKATA PORT TRUST KOLKATA DOCK SYSTEM Notice for Recruitment to the post of Executive Engineer (Mechanical / Electrical / Electronics) (Class-I Post) in Mechanical & Electrical Department Admit Cards have since been issued to the candidates (as per list below ) for appearing at written examination to be held on 13.03.2016 at 10.00 a.m. at the venue printed at the Admit Cards. If any of the listed candidates does not receive Admit Card by 11.03.2016, he/she may collect provisional Admit Card from the Recruitment Cell, to be operated temporarily at the Information & Facilitation Centre in the Ground Floor of Kolkata Port Trust at 15, Strand Road, Kolkata – 700 001 on 12.03.2016 (Saturday) from 11.00 A.M. to 03.00 P.M, personally or through any authorized representative, on submission of a print of the relevant page showing his/her name in the list, identity proof, address proof and proof of date of birth (DOB) of the candidate. Secretary (I/C) List of candidates Sl. No. Roll No. Candidate’s Name Father’s Name DOB 1 622664 A M NALCY PRABHA N ANDROW DANIEL 11071983 2 622635 A VISHALINI T ASHOK 17041991 3 622628 A. SENTHIL KUMAR 29051987 4 623376 AAHANA MEYUR NIRMAL KUMAR MEYUR 28101992 DR. ARDHENDU BIKASH 5 620608 AAHIRI SHARMA 03111993 SARMA AAKASH CHANDRAKUMAR 6 622792 14071993 BHATIA 7 620677 AAKASH DEEP PAUJARI JAISHANKAR PRASAD PUJARI 09071986 8 622009 AAMIR EQBAL ANWER EQBAL 14071991 9 623677 AAMIR NASEEM NASEEM AHMAD 01071993 10 621012 AAMOD KUMAR BHARAT OJHA 29101991 11 623686 AASHIT AGARWAL RAMAN AGARWAL 24021994 12 621907 AASHUTOSH KUMAR C.B.
    [Show full text]
  • Main Voter List 08.01.2018.Pdf
    Sl.NO ADM.NO NAME SO_DO_WO ADD1_R ADD2_R CITY_R STATE TEL_R MOBILE 61-B, Abul Fazal Apartments 22, Vasundhara 1 1150 ACHARJEE,AMITAVA S/o Shri Sudhamay Acharjee Enclave Delhi-110 096 Delhi 22620723 9312282751 22752142,22794 2 0181 ADHYARU,YASHANK S/o Shri Pravin K. Adhyaru 295, Supreme Enclave, Tower No.3, Mayur Vihar Phase-I Delhi-110 091 Delhi 745 9810813583 3 0155 AELTEMESH REIN S/o Late Shri M. Rein 107, Natraj Apartments 67, I.P. Extension Delhi-110 092 Delhi 9810214464 4 1298 AGARWAL,ALOK KRISHNA S/o Late Shri K.C. Agarwal A-56, Gulmohar Park New Delhi-110 049 Delhi 26851313 AGARWAL,DARSHANA 5 1337 (MRS.) (Faizi) W/o Shri O.P. Faizi Flat No. 258, Kailash Hills New Delhi-110 065 Delhi 51621300 6 0317 AGARWAL,MAM CHANDRA S/o Shri Ram Sharan Das Flat No.1133, Sector-29, Noida-201 301 Uttar Pradesh 0120-2453952 7 1427 AGARWAL,MOHAN BABU S/o Dr. C.B. Agarwal H.No. 78, Sukhdev Vihar New Delhi-110 025 Delhi 26919586 8 1021 AGARWAL,NEETA (MRS.) W/o Shri K.C. Agarwal B-608, Anand Lok Society Mayur Vihar Phase-I Delhi-110 091 Delhi 9312059240 9810139122 9 0687 AGARWAL,RAJEEV S/o Shri R.C. Agarwal 244, Bharat Apartment Sector-13, Rohini Delhi-110 085 Delhi 27554674 9810028877 11 1400 AGARWAL,S.K. S/o Shri Kishan Lal 78, Kirpal Apartments 44, I.P. Extension, Patparganj Delhi-110 092 Delhi 22721132 12 0933 AGARWAL,SUNIL KUMAR S/o Murlidhar Agarwal WB-106, Shakarpur, Delhi 9868036752 13 1199 AGARWAL,SURESH KUMAR S/o Shri Narain Dass B-28, Sector-53 Noida, (UP) Uttar Pradesh0120-2583477 9818791243 15 0242 AGGARWAL,ARUN S/o Shri Uma Shankar Agarwal Flat No.26, Trilok Apartments Plot No.85, Patparganj Delhi-110 092 Delhi 22433988 16 0194 AGGARWAL,MRIDUL (MRS.) W/o Shri Rajesh Aggarwal Flat No.214, Supreme Enclave Mayur Vihar Phase-I, Delhi-110 091 Delhi 22795565 17 0484 AGGARWAL,PRADEEP S/o Late R.P.
    [Show full text]
  • List of Officers Who Attended Courses at NCRB
    List of officers who attened courses at NCRB Sr.No State/Organisation Name Rank YEAR 2000 SQL & RDBMS (INGRES) From 03/04/2000 to 20/04/2000 1 Andhra Pradesh Shri P. GOPALAKRISHNAMURTHY SI 2 Andhra Pradesh Shri P. MURALI KRISHNA INSPECTOR 3 Assam Shri AMULYA KUMAR DEKA SI 4 Delhi Shri SANDEEP KUMAR ASI 5 Gujarat Shri KALPESH DHIRAJLAL BHATT PWSI 6 Gujarat Shri SHRIDHAR NATVARRAO THAKARE PWSI 7 Jammu & Kashmir Shri TAHIR AHMED SI 8 Jammu & Kashmir Shri VIJAY KUMAR SI 9 Maharashtra Shri ABHIMAN SARKAR HEAD CONSTABLE 10 Maharashtra Shri MODAK YASHWANT MOHANIRAJ INSPECTOR 11 Mizoram Shri C. LALCHHUANKIMA ASI 12 Mizoram Shri F. RAMNGHAKLIANA ASI 13 Mizoram Shri MS. LALNUNTHARI HMAR ASI 14 Mizoram Shri R. ROTLUANGA ASI 15 Punjab Shri GURDEV SINGH INSPECTOR 16 Punjab Shri SUKHCHAIN SINGH SI 17 Tamil Nadu Shri JERALD ALEXANDER SI 18 Tamil Nadu Shri S. CHARLES SI 19 Tamil Nadu Shri SMT. C. KALAVATHEY INSPECTOR 20 Uttar Pradesh Shri INDU BHUSHAN NAUTIYAL SI 21 Uttar Pradesh Shri OM PRAKASH ARYA INSPECTOR 22 West Bengal Shri PARTHA PRATIM GUHA ASI 23 West Bengal Shri PURNA CHANDRA DUTTA ASI PC OPERATION & OFFICE AUTOMATION From 01/05/2000 to 12/05/2000 1 Andhra Pradesh Shri LALSAHEB BANDANAPUDI DY.SP 2 Andhra Pradesh Shri V. RUDRA KUMAR DY.SP 3 Border Security Force Shri ASHOK ARJUN PATIL DY.COMDT. 4 Border Security Force Shri DANIEL ADHIKARI DY.COMDT. 5 Border Security Force Shri DR. VINAYA BHARATI CMO 6 CISF Shri JISHNU PRASANNA MUKHERJEE ASST.COMDT. 7 CISF Shri K.K. SHARMA ASST.COMDT.
    [Show full text]
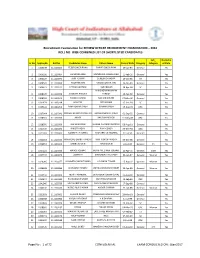
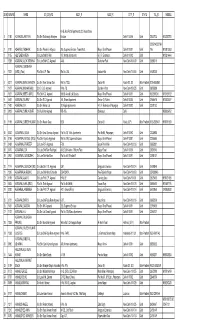
  • RO Stage1 Result 22-2-2017.Pdf
    Recruitment Examination for REVIEW OFFICER RECRUITMENT EXAMINATION – 2016 ROLL NO. WISE COMBINED LIST OF SHORTLISTED CANDIDATES Sub_ Domicille Sr No AppSeqNo Roll No Candidates Name Fathers Name Date of Birth Category Category of State 1 1000239 111110003 TEJBIR SINGH RANA RANVIR SINGH RANA 19-Jun-86 General Yes 2 1000250 111110004 SACHIN KUMAR MUNNA LAL VASHISHTHA 11-Feb-92 General Yes 3 1003107 111110070 AMIT KUMAR SURESH CHANDRA 19-Oct-86 ST Yes 4 1004501 111110092 ANUPAM JAIN VINOD KUMAR JAIN 16-Oct-93 General Yes 5 1006421 111110122 NEERAJ GAUTAM HAR PRASAD 18-Apr-94 SC Yes MAHENDRA NARAYAN 6 1008126 111110154 JITENDRA PANDEY PANDEY 15-Apr-90 General Yes 7 1008503 111110161 RAKESH KUMAR MOHAN SHYAM 07-Mar-90 General Yes 8 1011479 111110214 MUKESH POOJA RAM 15-Dec-93 SC Yes 9 1015402 111110294 RAM KUMAR SINGH ISHWAR SINGH 15-Aug-91 OBC Yes 10 1017644 111110341 PRANAV KUMAR PARASHAR UMASHANKAR SHARMA 01-Sep-92 General Yes 11 1018313 111110350 AKASH KAUSHAL KISHOR 11-May-88 OBC Yes 12 1018590 111110356 ASHISH KUMAR SURESH CHANDRA SHARMA 08-Aug-91 General Yes 13 1021166 111110402 HARSIT YADAV RAM KISHOR 03-Dec-94 OBC Yes 14 1021383 111110405 DAMNESH SHARMA CHATURBHUJ SHARMA 01-Jul-91 General Yes 15 1022153 111110422 HIMANSHU SHAKTI PANDAY RAM KISHOR PANDAY 05-Dec-86 General Yes 16 1024853 111110466 SAMBHAV JAIN ARVIND JAIN 24-Jul-93 General PH Yes 17 1027222 111120036 MANOJ SOLANKI INDRA PAL SINGH SOLANKI 15-Apr-75 General ESM Yes 18 1027437 111120042 LOKPRIYA MAHENDRA PAL SINGH 22-Jun-87 General Woman Yes 19 1029016 111120077 SUSHMITA
    [Show full text]
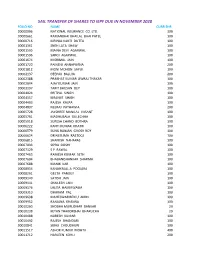
  • Sail Transfer of Shares to Iepf Due in November 2020 Folio No Name Curr Shr 00000006 National Insurance Co
    SAIL TRANSFER OF SHARES TO IEPF DUE IN NOVEMBER 2020 FOLIO NO NAME CURR SHR 00000006 NATIONAL INSURANCE CO. LTD. 300 00000661 RAMANBHAI BHAILAL BHAI PATEL 100 00000716 MRINAL KANTI DUTTA 100 00001361 SNEH LATA SHAW 100 00001595 MAINA DEVI AGARWAL 100 00001596 SAROJ AGARWAL 100 00001674 MISRIMAL JAIN 100 00001720 PAINENI ANNAPURNA 200 00001812 MONI MOHON SAPUI 100 00002137 DEEPAK BALUJA 200 00002388 PRABHAT KUMAR JIWRAJ THAKAR 100 00002894 AJAY KUMAR JAIN 100 00003197 TARIT BHUSAN DEY 100 00004024 PRITPAL SINGH 100 00004157 KIRANJIT SINGH 100 00004403 RAJESH KALRA 100 00004837 NEERAJ PATHAWIA 200 00005728 JAYSHREE MANILAL VASANT 100 00005761 MADHUBALA GULECHHA 100 00005918 SURESH CHAND BOTHRA 100 00006222 KANTI KUMAR KHATRI 100 00006579 SUNIL RANJAN GHOSH ROY 100 00006624 DR NEELIMA RASTOGI 100 00006815 SHAMISH NAHARAS 100 00007033 SIPRA DOSHI 100 00007129 S P RAWAL 100 00007463 RAMESH KUMAR SETH 100 00007604 BHABANISHANKAR SHARMA 100 00007688 MANIK KAR 100 00008054 KANAIYALAL A POOJARA 100 00008261 GEETA PANDEY 100 00009140 SATISH JAIN 100 00009141 SHAILESH JAIN 100 00009176 LALITA HAMIRWASIA 100 00009310 DHARAM PAL 100 00009698 MAHESWARIBEN U AMIN 100 00009952 RANJANA KHANNA 100 00010200 SHOBHA MURLIDHAR BANKAR 29 00010238 KETAN THAKORBHAI BHARUCHA 29 00010488 NARESH KUMAR 100 00010492 RAJESH BHANDARI 100 00010841 SIBAJI CHOUDHURI 100 00011517 ASHOK KUMAR MOHTA 400 00011712 HARLEEN KOHLI 200 00012304 SHYAM KISHORE RAWAT 100 00013496 TARIT BHUSHAN DEY 200 00013687 MANSUKH LAL AGARWAL 100 00013691 MAHENDRA KUMAR JAIN 100 00014620 MANORMA
    [Show full text]
  • Registration No. Name Father's Name DOB Bat Ch KMY000188213 ABHIMANYU MOHANTY SHYAMSUNDAR MOHANTY 01-11-1957 1 KMY000411213 AJAY
    Registration No.
    [Show full text]
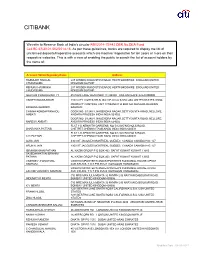
  • Details of Unclaimed Deposits / Inoperative Accounts
    CITIBANK We refer to Reserve Bank of India’s circular RBI/2014-15/442 DBR.No.DEA Fund Cell.BC.67/30.01.002/2014-15. As per these guidelines, banks are required to display the list of unclaimed deposits/inoperative accounts which are inactive/ inoperative for ten years or more on their respective websites. This is with a view of enabling the public to search the list of account holders by the name of: Account Holder/Signatory Name Address HASMUKH HARILAL 207 WISDEN ROAD STEVENAGE HERTFORDSHIRE ENGLAND UNITED CHUDASAMA KINGDOM SG15NP RENUKA HASMUKH 207 WISDEN ROAD STEVENAGE HERTFORDSHIRE ENGLAND UNITED CHUDASAMA KINGDOM SG15NP GAUTAM CHAKRAVARTTY 45 PARK LANE WESTPORT CT.06880 USA UNITED STATES 000000 VAIDEHI MAJMUNDAR 1109 CITY LIGHTS DR ALISO VIEJO CA 92656 USA UNITED STATES 92656 PRODUCT CONTROL UNIT CITIBANK P O BOX 548 MANAMA BAHRAIN KRISHNA GUDDETI BAHRAIN CHINNA KONDAPPANAIDU DOOR NO: 3/1240/1, NAGENDRA NAGAR,SETTYGUNTA ROAD, NELLORE, AMBATI ANDHRA PRADESH INDIA INDIA 524002 DOOR NO: 3/1240/1, NAGENDRA NAGAR,SETTYGUNTA ROAD, NELLORE, NARESH AMBATI ANDHRA PRADESH INDIA INDIA 524002 FLAT 1-D,KENWITH GARDENS, NO 5/12,MC'NICHOLS ROAD, SHARANYA PATTABI CHETPET,CHENNAI TAMILNADU INDIA INDIA 600031 FLAT 1-D,KENWITH GARDENS, NO 5/12,MC'NICHOLS ROAD, C D PATTABI . CHETPET,CHENNAI TAMILNADU INDIA INDIA 600031 ALKA JAIN 4303 ST.JACQUES MONTREAL QUEBEC CANADA CANADA H4C 1J7 ARUN K JAIN 4303 ST.JACQUES MONTREAL QUEBEC CANADA CANADA H4C 1J7 IBRAHIM KHAN PATHAN AL KAZMI GROUP P O BOX 403 SAFAT KUWAIT KUWAIT 13005 SAJEDAKHATUN IBRAHIM PATHAN AL KAZMI
    [Show full text]
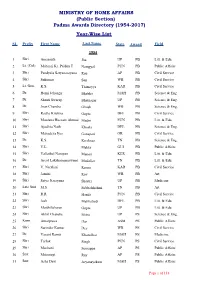
  • (Public Section) Padma Awards Directory (1954-2017) Year-Wise List
    MINISTRY OF HOME AFFAIRS (Public Section) Padma Awards Directory (1954-2017) Year-Wise List SL Prefix First Name Last Name State Award Field 1954 1 Shri Amarnath Jha UP PB Litt. & Edu. 2 Lt. (Col) Maharaj Kr. Palden T Namgyal PUN PB Public Affairs 3 Shri Pandyala Satyanarayana Rau AP PB Civil Service 4 Shri Sukumar Sen WB PB Civil Service 5 Lt. Gen. K.S. Thimayya KAR PB Civil Service 6 Dr. Homi Jehangir Bhabha MAH PB Science & Eng. 7 Dr. Shanti Swarup Bhatnagar UP PB Science & Eng. 8 Dr. Jnan Chandra Ghosh WB PB Science & Eng. 9 Shri Radha Krishna Gupta DEL PB Civil Service 10 Shri Moulana Hussain Ahmad Madni PUN PB Litt. & Edu. 11 Shri Ajudhia Nath Khosla DEL PB Science & Eng. 12 Shri Mahadeva Iyer Ganapati OR PB Civil Service 13 Dr. K.S. Krishnan TN PB Science & Eng. 14 Shri V.L. Mehta GUJ PB Public Affairs 15 Shri Vallathol Narayan Menon KER PB Litt. & Edu. 16 Dr. Arcot Lakshamanaswami Mudaliar TN PB Litt. & Edu. 17 Shri V. Narahari Raooo KAR PB Civil Service 18 Shri Jamini Roy WB PB Art 19 Shri Satya Narayana Shastri UP PB Medicine 20 Late Smt. M.S. Subbalakshmi TN PB Art 21 Shri R.R. Handa PUN PB Civil Service 22 Shri Josh Malihabadi DEL PB Litt. & Edu. 23 Shri Maithilisharan Gupta UP PB Litt. & Edu. 24 Shri Akhil Chandra Mitra UP PS Science & Eng. 25 Kum. Amalprava Das ASM PS Public Affairs 26 Shri Surinder Kumar Dey WB PS Civil Service 27 Dr. Vasant Ramji Khanolkar MAH PS Medicine 28 Shri Tarlok Singh PUN PS Civil Service 29 Shri Machani Somappa AP PS Public Affairs 30 Smt.
    [Show full text]
  • Ajit Ram Verma
    AJIT RAM VERMA 21 September 1921 ' 4 March 2009 Biog. Mem. Fell. INSA, New Delhi 39 (2011) 29-55 AJIT RAM VERMA 1921-2009 Elected Fellow 1963 FAMILY BACKGROUND AND EARLY EDUCATION JIT RAM VERMA was born on 21 September 1921 at Dalmau in Pratapgarh A Division of Uttar Pradesh. He often quoted his father that he was born on equinox day i.e. 23 September. His family originally belonged to Naushehra in Punjab and his grandfather Shri Daulat Ram Verma had left that place due to a family issue and started working in Indian Railways. He had passed middle class and could easily get a job in the Railways. Later, his father, Shri Hans Raj Verma had also served the Indian Railways all his life and rose to be a Station Master. He had many exceptional qualities. He was well versed with herbs and would treat people who approached him for the same. He was reputed for his astrological predictions. Verma had a strong influence of his mother Smt. Rani Devi all his life. A.R. Verma had his primary education at Pratapgarh in a school, which was not recogruzed. Therefore, his father sent him to Allahabad with one of his assistants who arranged his admission in a recognized school there and also arranged his stay with a family of a railway employee. It is remarkable that this family at that time did not have a child but after his short stay with them they were blessed with a child. Verma did his high school from CAB Higher Secondary School at Meerut Cantt.
    [Show full text]
  • Inside... Platinum Jubilee 1934-2009
    No. 50 September 2009 Newsletter of the Indian Academy of Sciences Platinum Jubilee 1934-2009 2009 Platinum Jubilee Meeting – I The annual meetings of the Academy are Inside... generally held at various cities other than Bangalore. Two exceptions are the Golden Jubilee meeting (which was to have been held 1. Platinum Jubilee Meeting – I, at Bangalore in November 1984, but was Hyderabad .......................................1 postponed to early 1985 on account of the tragic passing of Smt. Indira Gandhi) and the Diamond 2. Platinum Jubilee Meeting Jubilee Meeting in 1994. Similarly the series of Programmes, Bangalore ...............4 mid-year meetings initiated in 1990 have been 3. Associates – 2009 ..........................6 held at Bangalore each year, except for one occasion when it took place in Mysore. This D Balasubramanian 4. Special issues of Journals.............7 year 2009, being the Platinum Jubilee Year of the Academy, three meetings by way of 5. Refresher Courses..........................9 celebration have been organized: The usual Mid- Year Meeting was at Hyderabad, July 2–4; the 6. Lecture Workshops.......................12 Annual Meeting at Bangalore, November 12– 14; and one more at Mumbai during December 7. Women in Science........................19 3–5, as part of the Homi Bhabha centenary celebrations. These three meetings are 8. Post-School Science Teaching designated as Platinum Jubilee Meetings I, II, Programmes ..................................20 and III. 9. Building – Additional Space.......21 The first meeting
    [Show full text]
  • CIMFR Designs First Highwall Mining in India
    ISSN 0409-7467 CIMFR designs First Highwall Mining in India India's domestic energy requirement is met by coal combustion to the extent of about 60%. Currently the country produces about 500 MT of coal per year, 80% of which comes from opencast mines. There has been a great need to substantially increase the coal production in the coming decade to meet our growing economy. Unfortunately, many of Indian opencast mines are reaching their pit limits. Existence of surface dwellings in many places limits the expansion of currently running opencast mines. Also, in many cases the overburden becomes so high that coal extraction becomes uneconomical. But with the use of highwall machines, a cutter is placed on the top of a continuous miner kind of material, and taken through a conveyor inside the seam, which is almost 500-600 m deep inside. That was not possible till now, and large amounts remained untapped owing to limited means and high cost of mining of that seam. Highwall mining is a new technology which can extend the life of opencast mines without disturbing the surface dwellings, and maintaining economy and productivity. This technology is in use in United States and Australia but yet to be introduced in Indian coalfields. It is a remotely operated coal mining technology closely related to underground mining machinery. The method comprises extraction of coal from a series of parallel entries driven in the coal seam from the face of the highwall. These entries are unmanned, unsupported and unventilated. The Central Institute of Mining and Fuel Research (CIMFR), Dhanbad, is instrumental in adapting this new technology for Indian geomining conditions by providing scientific extraction design for the first two Highwall Mining sites at Ramagundem Opencast Project-II of M/s Singareni Collieries Company Ltd (SCCL) and Quarry SEB and AB, West Bokaro of M/s Tata Steel Ltd (TSL).
    [Show full text]