SLAC-210 UC-32 June 1978 (1) the EGS CODE SYSTEM
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dxpedition Report from Rose Spit, Haida Gwaii
Rose Spit mini-DXpedition 11 July, 2011. Rose Spit loggings for 11 July, 2011: Medium Wave and Long Wave Here is a compilation of what I heard on an overnight DC only DXpedition to Rose Spit, about 25 km from the closest power lines, on the north east corner of Haida Gwaii. This spit is sandy, and covered in short grasses and strawberry plants, so ideal for remote DXpeditions, as it is accessible by 4x4 wheel drive vehicles. Conditions were not very good with the A index around 13, and K indices between 2 and 4, and solar flux at 90.6. The loggings below on MW are almost all from using a 750’ BOG aimed at New Zealand, unterminated. Here’s an aerial photo of the Spit. I was located just a few hundred meters past the tree line, in about the center of the spit, which faces N/NE. The larger photo below shows Rose Spit looking back to the West/South West to the treeline. Lot’s of room for BOGs! The figure below shows a view in the opposite direction down the spit to the N/NW where the 750’ BOGs were located. The NZ wire could have easily been double the distance. A more likely scenario for next time might be a phased BOG array towards NZ or dual Wellbrook delta loops. My wonderful DXpedition vehicle: A Nissan Frontier, 4 door, 4x4. Very comfortable, with a folding down front passenger seat, making a perfect platform for the radios and computer. Also a comfortable rear seat to sleep. -
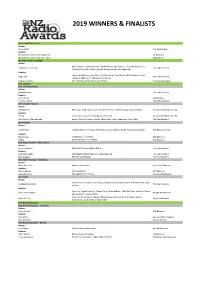
2019 Winners & Finalists
2019 WINNERS & FINALISTS Associated Craft Award Winner Alison Watt The Radio Bureau Finalists MediaWorks Trade Marketing Team MediaWorks MediaWorks Radio Integration Team MediaWorks Best Community Campaign Winner Dena Roberts, Dominic Harvey, Tom McKenzie, Bex Dewhurst, Ryan Rathbone, Lucy 5 Marathons in 5 Days The Edge Network Carthew, Lucy Hills, Clinton Randell, Megan Annear, Ricky Bannister Finalists Leanne Hutchinson, Jason Gunn, Jay-Jay Feeney, Todd Fisher, Matt Anderson, Shae Jingle Bail More FM Network Osborne, Abby Quinn, Mel Low, Talia Purser Petition for Pride Mel Toomey, Casey Sullivan, Daniel Mac The Edge Wellington Best Content Best Content Director Winner Ryan Rathbone The Edge Network Finalists Ross Flahive ZM Network Christian Boston More FM Network Best Creative Feature Winner Whostalk ZB Phil Guyan, Josh Couch, Grace Bucknell, Phil Yule, Mike Hosking, Daryl Habraken Newstalk ZB Network / CBA Finalists Tarore John Cowan, Josh Couch, Rangi Kipa, Phil Yule Newstalk ZB Network / CBA Poo Towns of New Zealand Jeremy Pickford, Duncan Heyde, Thane Kirby, Jack Honeybone, Roisin Kelly The Rock Network Best Podcast Winner Gone Fishing Adam Dudding, Amy Maas, Tim Watkin, Justin Gregory, Rangi Powick, Jason Dorday RNZ National / Stuff Finalists Black Sheep William Ray, Tim Watkin RNZ National BANG! Melody Thomas, Tim Watkin RNZ National Best Show Producer - Music Show Winner Jeremy Pickford The Rock Drive with Thane & Dunc The Rock Network Finalists Alexandra Mullin The Edge Breakfast with Dom, Meg & Randell The Edge Network Ryan -

New Zealand DX Times Monthly Journal of the D X New Zealand Radio DX League (Est 1948) D X April 2008 Volume 60 Number 6 LEAGUE LEAGUE
N.Z. RADIO N.Z. RADIO New Zealand DX Times Monthly Journal of the D X New Zealand Radio DX League (est 1948) D X April 2008 Volume 60 Number 6 LEAGUE http://www.radiodx.com LEAGUE Deadline for next issue is Wed 7th May 2008 . P.O. Box 39-596, Howick, Manukau 2145 CONTENTS FRONT COVER REGULAR COLUMNS Cover and partial page from 1948 Radio Bandwatch Under 9 3 Listeners Guide from League member with Ken Baird supplied by Dallas McKenzie Bandwatch Over 9 12 with Phil van de Paverd English in Time Order 16 with Yuri Muzyka Fcst SW Reception 19 Compiled by Mike Butler League 60th Anniversary Shortwave Report 20 with Ian Cattermole Thank you to Dallas McKenzie for the FM News and DX 24 with Adam Claydon front cover of the 1948 Radio Listeners TV and Satellite News 28 Guide used on this months DX Times with Adam Claydon Cover. Utilities 32 with Evan Murray If you have any similar material that you Combined Shortwave 34 think other members may be interested and Broadcast Mailbag in and may be suitable for publishing in with David Ricquish and Bryan Clark the DX Times please feel free to contact ADCOM News 45 me [email protected] with Bryan Clark Marketsquare 47 Branch News 48 Mark Nicholls with Chief Editor Chief Editor Ladders 51 with Stuart Forsyth OTHER CLOSING DATES FOR THE NEXT Tiwai Report 40 with Frank Glen 3 MONTHS (2008) Everglades Bandscan 42 You can send your contributions to the with Bruce Portzer NZ Radio DX League at AM Radio Lima 43 PO Box 39-596 On the Shortwaves 49 Howick compiled by Jerry Berg Manukau 2145 or use the email or postal addresses given by the section sub-editors. -

ML012320245.Pdf
APPENDIX D ASME REPAIRS AND REPLACEMENTS NIS-2 Forms APPENDIX D.1 MECHANICAL MAINTENANCE NIS-2 Forms ) PAGE 1 OF 7 UNIT 2 TENTH REFUELING AND INSPECTION OUTAGE MAINTENANCE CODE REPAIR AND REPLACEMENT 1.0 INTRODUCTION This summary identifies the work performed on ASME Section XI, classes 1, 2, 3 and MC of ASME Section VIII items for which Maintenance has NIS-2 responsibility reported in Section 3.1. Nation Board Inspection Code Repair items for which Maintenance has R-I responsibility is also included in Section 4.0. The majority of this work was performed during the Unit 2 Tenth Refueling and Inspection Outage. 2.0 CODE COMPLIANCE SUMMARY All work on ASME Section XI, classes 1, 2, 3 and MC, meets the requirements of IWA-4000 (Repair Procedures) and IWA-7000 (Replacements) of ASME Section XI, 1989 Edition, No Addenda. All work on containment meets the requirements of IWA-4000 and IWA 7000 of ASME Section XI, 1992 Edition through 1992 Addenda of IWE and IWL. 3.0 REPAIR AND REPLACEMENT SUMMARY Work in this category is comprised of Work Authorization of Seciton XI Repairs and Replacements. 3.1 SECTION XI REPAIRS AND REPLACEMENTS W.O. NO. 522 FORM NO. DISCRIPTION OF WORK SYSTEM NO. 211A, ASME CLASS III 102415 99-211-001 209091, Replaced Valve Disc SYSTEM NO. 216A, ASME CLASS III 229132 01-216-001 PSV-21213A, Replaced Valve Disc 312089 01-216-002 HV21210B, Replaced Valve and Leak Off Plug 324011 01-216-003 212016, Replaced Stem/Disc & Backseat Bushing SYSTEM NO. 225A. ASME CLASS H 266728 00-225-001 226018 & 226029, Replaced Valve SYSTEM NO.234D, -
BSA Annual Report 1992
BROADCASTING STANDARDS AUTHORITY TE MANA WHANONGA KAIPAHO ANNUAL REPORT FOR THE YEAR ENDED 30 JUNE 1992 MISSION STATEMENT To establish and maintain acceptable standards of broadcasting on all New Zealand radio and television, within the context of current social values, research and the principle of self-regulation, in a changing and deregulated industry Submitted to the Minister of Broadcasting for presentation to the House of Representatives pursuant to clause 14 of the First Schedule of the Broadcasting Act 1989- Iain Gallaway Chairperson The annual financial reports have been published separately and can be obtained, as can the other material mentioned in this document by writing to: or by visiting the: Broadcasting Standards Authority 2nd Floor PO Box 9213 NZ Lotteries Commission Building Wellington 54 - 56 Cambridge Tee New Zealand Wellington Phone: (04) 382 9508 Fax: (04) 382 9543 CONTENTS CHAIRPERSON'S FOREWORD 4 MEMBERS 5 A YEAR OF REVIEWS 6 COMPLAINTS 8 Overview Analysis of Decisions Procedures Parallel jurisdiction Privacy REVIEW OF THE CODES 12 Alcohol advertising Portrayal of violence on television Children's television programme standards Other codes RESEARCH PROGRAMME 17 Commissioned research In-house research Consultations PUBLICATIONS, EDUCATION AND PROMOTION 19 Complaints procedures General advertising and promotion Reference library Publications POLITICAL PARTY ADVERTISING 20 STAFF 21 STATEMENTS OF SERVICE PERFORMANCE 22 APPENDICES 27 Complaints determined by the Authority Advisory opinion on privacy List of Publications -

RNZ Concert and RNZ's Music Strategy
Documents in Scope of OIA Requests for Official Advice Relating to RNZ Concert and RNZ’s Music Strategy Published 16 June 2020 Author: Ministry for Culture and Heritage These documents have been proactively released. Some parts of these documents have been withheld under the Official Information Act 1982 (the OIA). Where this is the case, the relevant sections of the OIA that would apply have been identified. Where information has been withheld, no public interest has been identified that would outweigh the reasons for withholding it. Information has been withheld under the following grounds of the OIA: • section 9(2)(a) – to protect the privacy of natural persons; • section 9(2)(f)(iv) – to maintain the current constitutional conventions protecting the confidentiality of advice tendered by Ministers and officials; • section 9(2)(h) – to maintain legal privilege; and • section 9(2)(g)(i) – to maintain the effective conduct of public affairs through the free and frank expression of opinions. Hon Kris Faafoi Minister of Broadcasting, Communications and Digital Media cc Minister for Arts, Culture and Heritage AIDE MEMOIRE: MEETING WITH RNZ CHAIR AND CE – MUSIC STRATEGY Date: 27 January 2020 Priority: High Security In Confidence Reference: AM 2020/008 classification: Contact Ruth Palmer, Director, Policy S9(2)(a) Purpose 1 This aide memoire provides background for your meeting with Dr Jim Mather, Chair, Paul Thompson, Chief Executive, and Peter Parussini, board member, of RNZ, on Wednesday 29 January, from 5:00 to 5:30 p.m. The meeting is to discuss proposed changes in RNZ’s music strategy. 2 The Treasury has been consulted in the preparation of this briefing. -

Monday, August 16, 2021 Home-Delivered $1.90, Retail $2.20 Getcha Motor Running for Meth Awareness Page 3
TE NUPEPA O TE TAIRAWHITI MONDAY, AUGUST 16, 2021 HOME-DELIVERED $1.90, RETAIL $2.20 GETCHA MOTOR RUNNING FOR METH AWARENESS PAGE 3 KABU FALLS TALIBAN SEIZES POWER PAGE 12 BLASTS FROM THE PAST: All Black star power of the past came to the Coast on Saturday when the Classic All Blacks took HAITI QUAKE on Ngati Porou East Coast in Tokomaru Bay. Corey Flynn, who played 15 tests for the ABs between 2003 and 2011, autographs a ball for Harry Searle with another 15-test international, Jason DEATH TOLL Eaton, next to them. Left, Eroni Clark, who played 10 tests from 1992 to 1998 and is New Zealand Rugby’s Pasifika engagement manager, tests the Coast defence with 31-test player Luke OVER 720 McAlister in support. The Classic ABs contingent was led here by rugby great Sir Wayne “Buck” Shelford as part of the reality TV show Match Fit, which is in the production stage. Match Fit follows the experiences of a group of former ABs trying to get back in shape. Among others to take part in Saturday’s game were ex-All Blacks and brothers Rico and Hosea Gear — Hosea is the NPEC coach for this year’s Heartland Championship — and some “local legends”. The Classic ABs won the match 37-20. MORE PICTURES ON PAGE 5 Pictures by Paul Rickard PAGE 14 Cleared for takeoff Trust let off with warning after unconsented work on wetlands by Alice Angeloni But instead the trust applied for a resource consent to cover the works AN airstrip built in a protected TE ARAROA already done and those still needed to wetland area was granted consent AIRSTRIP: Te finish the 900-metre grassed runway, retrospectively despite objections from Rimu Trust built including upgrades to an existing farm Gisborne District Council’s own ecologist an airstrip on its track and building a carpark. -

Weekender, May 9, 2020
SATURDAY, MAY 9, 2020 Gisborne’s former Cook Hospital, where Marshall Hyland and other polio patients spent several weeks of their lives being Polio epidemic treated for the disease in a dedicated hospital ward, like those typical of others throughout the country. remembered Gisborne Herald fi le photo At 72, Marshall Hyland still remembers the exact date and what he was doing when, as an eight-year-old growing up in Gisborne, he suddenly fell ill with polio. e memory of it is etched on his mind, he says. Marshall had bulbar paralytic poliomyelitis — the most severe of three types of polio. He revisits the experience, for our readers, from his Whakatane home during the Covid-19 lockdown. It was Friday night, the fourth of etched in my mind. e polio ward was in window and, lo and behold, it was my father because they were like little Gods then. All November, 1955 — I was playing the south east corner of Cook Hospital. You bringing me books from home. Other than the nurses would be scurrying around about “cricket in our backyard with a went in there and you stayed there, with no that, there weren’t any visitors while I was in 9am and everyone would be made ready with neighbour and I felt feverish, like I visitors, until you came out ‘one way or the there — I don’t think visitors were allowed. the blankets pulled down on the beds. e was getting the ‘fl u so mum put me to bed other’. “One of the touching things I got in doctors didn’t talk to us. -

Annual Report 2008-2009 PDF 5.9 MB
NZ On Air Annual Report For the year ended 30 June 2009 Proudly supporting local content for 20 years 1989-2009 Annual Report For the year ended 30 June 2009 Table of contents Table of contents Part 1 Our year 1 Highlights 1 Who we are 2 Mission statement and values 2 Chair’s introduction 3 Key achievements 4 Television funding 4 Maori broadcasting 10 Radio funding 11 Digital funding 13 NZ Music funding 14 Archiving funding 16 Research 17 Consultation 18 Operations 18 Main performance measures 20 Part 2 Accountability statements 21 Statement of responsibility 21 Audit report 22 Statement of financial performance 23 Statement of financial position 24 Statement of changes in equity 25 Statement of cash flows 26 Notes to the financial statements 27 Statement of service performance 42 Appendices 1. Television funding 51 2. Radio funding 55 3. NZ Music funding 56 4. Music promotion 58 5. Digital and Archiving funding 58 6. Maori broadcasting 59 Directory 60 Download the companion PDF document to see: 20 years of NZ On Air NZ On Air Annual Report to 30 June 2009 1 Part 1: Our Year Highlights • The website NZ On Screen was launched, showcasing historic New Our investments helped create some Zealand television and film online and outstanding success stories this year: winning a Qantas Media Award in its first year • The Top 10 funded television • Our Ethnic Diversity Forum brought programmes had some of our highest all relevant broadcasters together viewing numbers ever around a subject of increasing importance • New Zealand drama successfully -

Annual Report 2019-2020
Kei te paemua hoki Te Reo Irirangi o Aotearoa i te wānanga nui mō te āpōpō o te ao pāpāho tūmatanui i Aotearoa. Ka mahi tahi tonu mātou me te Kāwanatanga ki ngā kōwhiringa mō te taha ki tana kaupapa Pou Pāpāho Tūmatanui Pakari, ka mutu, ka whakapakarihia anō tā mātou tuku kaupapa ki ētahi kāhui apataki whānui ake, kanorau anō. RNZ has been at the forefront of the debate on the future of public media in Aotearoa. We will continue to work with the Government on its Strong Public Media opportunities and further strengthen our content delivery to wider and diverse audiences. Dr Jim Mather / Tākuta Jim Mather Chair / Heamana, RNZ RNZ IS PERCEIVED AS THE MOST TRUSTED MEDIA ORGANISATION IN NEW ZEALAND COLMAR BRUNTON VALUE INDICES RESEARCH 2020 05 THE YEAR IN REVIEW 12 OUR CHARTER 14 RNZ LEADERSHIP TEAM 15 RNZ BOARD OF GOVERNORS 16 CHAIR’S REPORT 18 CEO’S REPORT 21 FINANCIAL PERFORMANCE 46 SERVICE PERFORMANCE 57 RNZ MĀORI STRATEGY 58 GOOD EMPLOYER REPORT HOE RNZ REPRESENTATION for ACCOUNTABILITY / KAKAU ANNUAL REPORT 2019/20 The kakau/handle must be sturdy without cracks that can weaken it. It Four key areas of strategy and governance represents the accountability of the are represented by the parts of the hoe/ Board in meeting Charter obligations paddle used to guide and steer the waka. to provide a multimedia public broadcasting service that is important to, and valued by, New Zealanders. LEADERSHIP / TINANA The tinana/body can take many shapes and lengths and is used to drive the hoe through the water. -
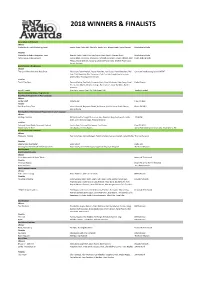
2018 Winners & Finalists
2018 WINNERS & FINALISTS Associated Craft Award Winner MediaWorks Trade Marketing Team Jessica Knox, Cathy Fali, Alex Jolly, Isaiah Tour, Megan Leach, Emily Hargest MediaWorks Radio Finalists MediaWorks Radio Integration Team Danielle Tolich, Nikki Flint, Rob Dickey, Nicki Covich, Morgan Penn MediaWorks Radio NZME Group Creative Team Justine Black, Jon Coles, Tracey Fox, Ashleigh van Graan, Fraser Tebbutt, John NZME Radio Brands Pelasio, Nicola Milliner, Kayoung Lee,Abbie-Rose Foley, Michael Pati Fuiava, Lincoln Putnam Best Children's Programme Winner The Crazy Kiwi Christmas Kids Show Phil Guyan, Bjorn Brickell, Dayna Vawdrey, Levi Guyan, Daryl Habraken, Phil Christian Broadcasting Assoc & NZME Yule, Chris Newbold, Erin Carpenter, Colin Cassidy, Steph Couch, Jacinda Ardern, Mike Hosking, Kerre McIvor Finalists That's The Story Ronnie Mackie, Zoe Nash, Cameron Nash, Chris Hitchcock, Kate Carey, Carol Radio Rhema Green, John Martin, Hebron College, Racheal Joel, Linda Tomikino, Rachel Hamilton Suzy & Friends Suzy Cato, Trevor Plant, Phil Yule, Brent Holt Treehut Limited Best Community Access Programmes Best Music Programme in Any Language Winner Lekker Stuff Karisma Nel Free FM 89.0 Finalist Desi Boys Party Time Vinesh Prakash, Rajneeta Chand, Avi Kumar, Krish Krishna, Shahil Sharan, Plains FM 96.9 Akshay Reddy Best Spoken/ Informational Programme in any Language Winner Heritage Matters Bill Southworth, Dougal Stevenson, Jane Edwards, Judy Southworth, Keith 105.4 FM Scott, Anne Barrowclough, Richard Stedman Finalists Safe and Sound Radio -

The Early Local Pop Recording Industry Was Dominated by Three American Genres
1950–1959 The early local pop recording industry was dominated by three American genres. Female singers and male vocal groups performed mainstream pop, a wave of recording in a faux-Hawaiian style occurred, and a posse of country and western artists arrived. On the live scene, big bands still featured in cabarets and ballrooms, while in Auckland the Maori Community Centre was a Mecca for aspiring talent. Hawaiian music’s long popularity in New Zealand had begun in 1911, and a key part of the attraction of ‘Blue Smoke’ in 1949 was its use of the steel guitar. In Auckland, the style was led by two Tongan steel-guitar players who became stalwarts of the live and recording scenes: Bill Sevesi and Bill Wolfgramm. Daphne Walker, a Maori from Great Barrier Island, was the most prominent singer, and it was Sam Freedman – a Russian Jewish songwriter based in Wellington – who wrote the biggest local hits. Country and western has a history in New Zealand that is almost as long, and evolved from recordings and film. Country recordings by US acts were available in New Zealand in the late 1920s, and western films also inspired those wanting to emulate the cowboy sound (and look). New Zealand’s earliest prominent country artist, Tex Morton, remains the most influential. Radio also spread the popularity of country music, through request shows, live broadcasts from regional stations, and specialist shows hosted by Happi Hill and Cotton-Eye Joe (Arthur Pearce). Also important was a square-dancing fad in the early 1950s. The new independent labels jumped onto the country bandwagon immediately, with Tanza finding wide acceptance for the Tumbleweeds, who toured nationally.