Predictability of Financial Market Indexes by Deep Neural Network
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
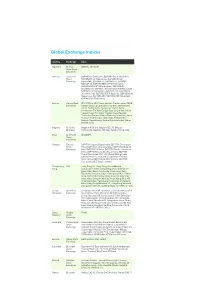
Global Exchange Indices
Global Exchange Indices Country Exchange Index Argentina Buenos MERVAL, BURCAP Aires Stock Exchange Australia Australian S&P/ASX All Ordinaries, S&P/ASX Small Ordinaries, Stock S&P/ASX Small Resources, S&P/ASX Small Exchange Industriials, S&P/ASX 20, S&P/ASX 50, S&P/ASX MIDCAP 50, S&P/ASX MIDCAP 50 Resources, S&P/ASX MIDCAP 50 Industrials, S&P/ASX All Australian 50, S&P/ASX 100, S&P/ASX 100 Resources, S&P/ASX 100 Industrials, S&P/ASX 200, S&P/ASX All Australian 200, S&P/ASX 200 Industrials, S&P/ASX 200 Resources, S&P/ASX 300, S&P/ASX 300 Industrials, S&P/ASX 300 Resources Austria Vienna Stock ATX, ATX Five, ATX Prime, Austrian Traded Index, CECE Exchange Overall Index, CECExt Index, Chinese Traded Index, Czech Traded Index, Hungarian Traded Index, Immobilien ATX, New Europe Blue Chip Index, Polish Traded Index, Romanian Traded Index, Russian Depository Extended Index, Russian Depository Index, Russian Traded Index, SE Europe Traded Index, Serbian Traded Index, Vienna Dynamic Index, Weiner Boerse Index Belgium Euronext Belgium All Share, Belgium BEL20, Belgium Brussels Continuous, Belgium Mid Cap, Belgium Small Cap Brazil Sao Paulo IBOVESPA Stock Exchange Canada Toronto S&P/TSX Capped Equity Index, S&P/TSX Completion Stock Index, S&P/TSX Composite Index, S&P/TSX Equity 60 Exchange Index S&P/TSX 60 Index, S&P/TSX Equity Completion Index, S&P/TSX Equity SmallCap Index, S&P/TSX Global Gold Index, S&P/TSX Global Mining Index, S&P/TSX Income Trust Index, S&P/TSX Preferred Share Index, S&P/TSX SmallCap Index, S&P/TSX Composite GICS Sector Indexes -

Animal Spirits
Pan Asia Strategy 23 November 2017 Animal Spirits Reconciling Nifty-style and Asian small cap equities Continuing the Nifty-style theme, we suggest having some exposure to Asian small caps to hedge concentration risk as growth returns Asian small caps are outgrowing the broader indices, and while size alone favours the mega caps, JASDAQ and KOSDAQ surprise Based on factor and thematic selection, we add Canvest Environment Paul M. Kitney, PhD Protection and Lee & Man Paper to our top picks (852) 2848 4947 [email protected] Asian small caps and diversifying market concentration risk. While large cap and especially mega cap equities have made an outsized contribution to equity returns, our analysis demonstrates evidence that growth stocks are now generating alpha. Small cap names, particularly those with sustainable growth, provide diversification from Nifty-style market concentration. Small cap growth is superior and the price for growth is reasonable. MSCI Asia ex-Japan small cap earnings growth is markedly outpacing the broader MSCI Asia ex-Japan index, and the PEG is meaningfully lower for 2018 and 2019. Animal Spirits top picks Company Ticker JASDAQ and KOSDAQ outperform with concrete earnings drivers. New China Life Insurance 1336 HK While the JASDAQ has outperformed the TOPIX since January 2017, the PICC 1339 HK KOSDAQ has only started to outperform the KOSPI since October 2017 Hana Financial 086790 KS Yes Bank YES IN but is making up for lost time. Earnings growth for both over-the-counter SK Hynix 000660 KS (OTC) markets is more rapid than the broader indices, but we find the NCsoft 036570 KS JASDAQ is more attractively priced, relatively. -

France Fund A-Euro for Investment Professionals Only FIDELITY FUNDS MONTHLY PROFESSIONAL FACTSHEET FRANCE FUND A-EURO 31 AUGUST 2021
pro.en.xx.20210831.LU0048579410.pdf France Fund A-Euro For Investment Professionals Only FIDELITY FUNDS MONTHLY PROFESSIONAL FACTSHEET FRANCE FUND A-EURO 31 AUGUST 2021 Strategy Fund Facts Bertrand Puiffe uses an unconstrained approach to portfolio construction, investing in Launch date: 01.10.90 companies based on their merits and not taking into account their prominence in the Portfolio manager: Bertrand Puiffe index. He takes a long-term view that allows him to benefit from market inefficiencies Appointed to fund: 01.09.17 created by the shorter-term time horizon of other investors. Bertrand has a very Years at Fidelity: 15 disciplined investment process based on systematic scoring of companies on Fund size: €64m qualitative and quantitative factors. He typically invests in three types of companies: Number of positions in fund*: 35 turnaround stories, special situations and where the market underestimates how strong, Fund reference currency: Euro (EUR) and for how long, growth can be sustained. Bertrand has a disciplined approach to risk Fund domicile: Luxembourg management at the stock level and during the portfolio construction process. Fund legal structure: SICAV Management company: FIL Investment Management (Luxembourg) S.A. Capital guarantee: No Portfolio Turnover Cost (PTC): 0.02% Portfolio Turnover Rate (PTR): 21.73% *A definition of positions can be found on page 3 of this factsheet in the section titled “How data is calculated and presented.” Objectives & Investment Policy Share Class Facts • The fund aims to provide long-term capital growth with the level of income expected Other share classes may be available. Please refer to the prospectus for more details. -

(Ex Controversies and CW) Index Equity Fund
Report and Financial Statements For the year ended 31st December 2020 State Street AUT Japan Screened (ex Controversies and CW) Index Equity Fund (formerly State Street Japan Equity Tracker Fund) State Street AUT Japan Screened (ex Controversies and CW) Index Equity Fund Contents Page Manager's Report* 1 Portfolio Statement* 5 Director's Report to Unitholders* 25 Manager's Statement of Responsibilities 26 Statement of the Depositary’s Responsibilities 27 Report of the Depositary to the Unitholders 27 Independent Auditors’ Report 28 Comparative Table* 31 Financial statements: 32 Statement of Total Return 32 Statement of Change in Net Assets Attributable to Unitholders 32 Balance Sheet 33 Notes to the Financial Statements 34 Distribution Tables 45 Directory* 46 Appendix I – Remuneration Policy (Unaudited) 47 Appendix II – Assessment of Value (Unaudited) 49 * These collectively comprise the Manager’s Report. State Street AUT Japan Screened (ex Controversies and CW) Index Equity Fund Manager’s Report For the year ended 31st December 2020 Authorised Status The State Street AUT Japan Screened (ex Controversies and CW) Index Equity Fund (the “Fund”) is an Authorised Unit Trust Scheme as defined in section 243 of the Financial Services and Markets Act 2000 and it is a UCITS Retail Scheme within the meaning of the FCA Collective Investment Schemes sourcebook. The unitholders are not liable for the debts of the Fund. The Fund's name was changed to State Street AUT Japan Screened (ex Controversies and CW) Index Equity Fund on 18th December 2020 (formerly State Street Japan Equity Tracker Fund). Investment Objective and Policy The objective of the Fund is to replicate, as closely as possible, and on a “gross of fees” basis, the return of the Japan equity market as represented by the FTSE Japan ex Controversies ex CW Index (the “Index”) net of unavoidable withholding taxes. -

ETF/ETN Monthly Report Feb-2014
issue month ETF/ETN Monthly Report Feb-2014 ◆Market Summary Average daily trading value surges past last month's record high! ■ In January, the ETF/ETN market reached a new record high in ADV of about JPY 146 billion. Monthly trading value was at about JPY 2.77 trillion, staying close to last month's high. ■ NEXT FUNDS Nikkei 225 Leveraged Index Exchange Traded Fund (1570) accounted for the majority of the trading value. TOPIX Bull 2x ETF (1568) also saw growing activity. ■ The market welcomed two new ETFs tracking the JPX-Nikkei Index 400 on January 28 (Tue.). NEXT FUNDS JPX-Nikkei Index 400 Exchange Traded Fund (1591) and Listed Index Fund JPX-Nikkei 400 (1592) both got off to a smooth start. The former ranked 18th in monthly trading value despite being traded for only four days while the latter came in at 25th in the rankings (the table in the attachment only includes the top 20 issues). ◆Trading Value - Monthly(Auction) (Jan-2014) Total(JPY) Daily Average (JPY) ◆Trading days:19 Month on Month 2,768,245,883,073 145,697,151,741 +4.05% ◆Rankings ETF 149 ● Monthly trading value (Jan-2014) ETN 22 Monthly Trading Value, Value Fund # Code Name Underlying index/commodity Category Monthly Change (%) (unit: JPY 1,000) Administrator 1 1570 NEXT FUNDS Nikkei 225 Leveraged Index Exchange Traded Fund Nikkei 225 Leveraged Index Domestic Stock Indices 1,533,713,500 +3.69% Nomura AM 2 1321 Nikkei 225 Exchange Traded Fund Nikkei 225 Domestic Stock Indices 285,213,285 -4.21% Nomura AM 3 1568 TOPIX Bull 2x ETF TOPIX Leveraged (2x) Index Leveraged / Inverse -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

Execution Version
Execution Version GUARANTEED SENIOR SECURED NOTES PROGRAMME issued by GOLDMAN SACHS INTERNATIONAL in respect of which the payment and delivery obligations are guaranteed by THE GOLDMAN SACHS GROUP, INC. (the “PROGRAMME”) PRICING SUPPLEMENT DATED 23rd SEPTEMBER 2020 SERIES 2020-12 SENIOR SECURED EXTENDIBLE FIXED RATE NOTES (the “SERIES”) ISIN: XS2233188510 Common Code: 223318851 This document constitutes the Pricing Supplement of the above Series of Secured Notes (the “Secured Notes”) and must be read in conjunction with the Base Listing Particulars dated 25 September 2019, as supplemented from time to time (the “Base Prospectus”), and in particular, the Base Terms and Conditions of the Secured Notes, as set out therein. Full information on the Issuer, The Goldman Sachs Group. Inc. (the “Guarantor”), and the terms and conditions of the Secured Notes, is only available on the basis of the combination of this Pricing Supplement and the Base Listing Particulars as so supplemented. The Base Listing Particulars has been published at www.ise.ie and is available for viewing during normal business hours at the registered office of the Issuer, and copies may be obtained from the specified office of the listing agent in Ireland. The Issuer accepts responsibility for the information contained in this Pricing Supplement. To the best of the knowledge and belief of the Issuer and the Guarantor the information contained in the Base Listing Particulars, as completed by this Pricing Supplement in relation to the Series of Secured Notes referred to above, is true and accurate in all material respects and, in the context of the issue of this Series, there are no other material facts the omission of which would make any statement in such information misleading. -

Tokyo Stock Price Index
s Tokyo Stock Price Index Tokyo Stock Price Index (TOPIX) is a measure of the overall trend in the stock market, and is used as a benchmark for investment in Japanese stocks. Outline Number of Constituents 2187 - Tokyo Stock Price Index (TOPIX) is calculated by Tokyo Stock Exchange. ( As of 2021.3.31 ) Base Date 1968/1/4 - TOPIX is a market benchmark with functionality as an investable index, Base Point 100 covering a wide range of Japanese stock market. TOPIX is a free-float adjusted market capitalization-weighted index. Information vendor codes - TOPIX is calculated based on all the domestic common stocks listed on (1st line:price return,2nd line:total return, the TSE First Section until April 1, 2022(the business day before the 3rd line:net total return) market restructure). - The price return index is calculated and disseminated in real-time (1 sec). Quick 151 - The total return index is calculated on a daily basis. S151/TSX S151#NR/TSE Index Performance (1968.1.4 = 100point) Bloomberg TPX <INDEX> 3500 TPXDDVD <INDEX> TPXNTR<INDEX> 3000 2500 Refinitiv .TOPX .TOPXDV 2000 .TOPXDVNET 1500 1000 ETFs 500 TOPIX Please refer to the following 0 URL for ETFs. URL: 1977 1979 1969 1971 1973 1975 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001 2003 2005 2007 2009 2011 2013 2015 2017 2019 1968 https://www.jpx.co.jp/english/e Total Return Index (ROI) ( As of 2021.3.31 ) quities/products/etfs/issues/0 1.html 1month 3month 6month 12month (【JPX Website Top Page】→ TOPIX 5.71% 9.25% 21.48% 42.13% 【Equities】→【Products】→ 【ETFs】→【Listed Issues】) Component Stocks (top 10 by free-float market capitalization) ( As of 2021.3.31 ) local codeName Sector Weight 1 7203 TOYOTA MOTOR CORPORATION Transportation Equipment 3.26% 2 9984 SoftBank Group Corp. -

Information Circular: NETS Trust Background Information on the Funds
Information Circular: NETS Trust To: Head Traders, Technical Contacts, Compliance Officers, Heads of ETF Trading, Structured Products Traders From: BX Listing Qualifications Department DATE: January 15, 2009 Exchange-Traded Fund Symbol CUSIP # NETS CAC40 Index Fund FRC 64118K209 NETS TOPIX Index Fund TYI 64118K407 NETS Hang Seng Index Fund HKG 64118K308 Background Information on the Funds The NETS Trust (the “Trust”) is a management investment company registered under the Investment Company Act of 1940, as amended (the “1940 Act”). The Trust consists of several exchange-traded funds (each, a “Fund” and collectively, the “Funds”). This circular refers only to the three Funds listed above. The shares of each of the Funds listed above are referred to herein as “Shares.” Northern Trust Investments, N.A. (the “Adviser”) serves as the investment adviser for the Funds. Each Fund is an “index fund” that seeks investment results that correspond generally to the price and yield performance, before fees and expenses, of a particular index (its “Underlying Index”). Each Underlying Index is a group of securities that the sponsor of an index (an “Index Provider”) selects as representative of a specific market, market segment or industry sector. Each Index Provider determines the relative weightings of the securities in the index and publishes information regarding the market value of the index. Additional information regarding each Index Provider is provided in the prospectus for the Funds. FRC seeks to provide investment results that correspond generally to the price and yield performance, before fees and expenses, of publicly-traded securities in the aggregate in the French market, as represented by the CAC40 (the “CAC Index”). -

Thomson One Quick Reference Guide
THOMSON ONE QUICK REFERENCE GUIDE Thomson ONE (www.thomsonone.com) provides integrated access to comprehensive market and company information. All of the intelligence you need to power your knowledge gathering and drive smarter decision-making. This Quick Reference Card offers some quick tips on customizing your workspace, setting up alerts, searching and more. LOOKING UP A COMPANY To add a service to your Favorites, open the page, click , and then select Add to Favorites. PUBLIC COMPANIES: To organize your favorites 1. If the company symbol is not known, click the 1. Click , and select Organize Favorites. Search icon. 2. If you want to create and name folders, click 2. Select either Contains or Begins With, then type all or Create Folder, and type in a name. part of the company name. 3. Drag a favorite into any folder, or click up or down 3. (Optional) Click the Home Listing Only check box to arrows to move it to a different place in the list. limit results to a company’s primary (Home) exchange. 4. Click OK. 4. Click Search. 5. Select the company symbol to display content related To set any page as your Home Page to that company. Click , and select Set as Home. PRIVATE COMPANIES: To return to your home page at any time, click . 1. Click the Symbol drop-down, and select Private Co. FLEX MONITOR: MONITORING A 2. Type the private company name (use , if needed), and click Go. COVERAGE LIST 3. Select the private company name to display content Flex Monitor allows you to create and save an unlimited related to that company. -

ANALYSIS of the JAPANESE INDICES Analýza Japonských Indexů Bachelor Thesis
Masaryk University Faculty of Economics and Administration Field of study: Finance ANALYSIS OF THE JAPANESE INDICES Analýza japonských indexů Bachelor thesis Thesis supervisor: Author: doc. Ing. Martin SVOBODA, Ph.D. Sabina BINZARU Brno, 2014 Author’s name and surname: Sabina Binzaru Name of bachelor thesis: Analysis of the Japanese indices Department: Finance Bachelor thesis supervisor: doc. Ing. Martin SVOBODA, Ph.D. Year of defense: 2014 Annotation This bachelor thesis focuses on the Japanese stock indices, particularly on Nikkei 225 and TOPIX. The main goal of the thesis is to analyze the main characteristics of the previously mentioned indices, evaluate and compare their way of construction, regard the possibility of index investing and formulate recommendations on this issue. The thesis consists of four chapters; the first chapter makes an introduction to indices mentioning their history, fundamental uses and factors of relevance. The second chapter focuses on index construction taking into account weighting, calculation and adjustment methods. The third chapter briefly introduces Japanese stock indices and then analyzes and compares the chosen Japanese indices from different perspectives. The last chapter is aiming at describing index investment opportunities and risks and discovering and comparing index investing products that have Nikkei 225 and TOPIX as underlying. Anotace Tato bakalářská práce se zaměřuje na japonských akciových indexů, zejména na Nikkei 225 a TOPIX. Hlavním cílem práce je analyzovat základní charakteristiky výše uvedených indexů, hodnotit a porovnávat jejich způsob konstrukce, možnost investování do indexů a formulovat doporučení týkající se této problematiky. Práce se skládá ze čtyř kapitol; první kapitola je úvodem do indexů zmiňující jejich historii, základní použití a faktory které ovlivňují vypovídací schopnost indexu. -

A Quantitative Study of Stock Market Correlation
Diversifying in the Integrated Markets of ASEAN+3 - A Quantitative Study of Stock Market Correlation Authors: Emelie Nordell Caroline Stark Supervisor: Anders Isaksson Student Umeå School of Business Spring semester 2010 Bachelor thesis, 15 hp Acknowledgement Anders Isaksson, thank you for your support! Linus Jansson, we dedicate our thesis to you. I Abstract There is evidence that globalization, economic assimilation and integration among countries and their financial markets have increased correlation among stock markets and the correlation may in turn impact investors’ allocation of their assets and economic policies. We have conducted a quantitative study with daily stock index quotes for the period January 2000 and December 2009 in order to measure the eventual correlation between the markets of ASEAN+3. This economic integration consists of; Indonesia, Malaysia, Philippines, Singapore, Thailand, China, Japan and South Korea. Our problem formulation is: Are the stock markets of ASEAN+3 correlated? Does the eventual correlation change under turbulent market conditions? In terms of the eventual correlation, discuss: is it possible to diversify an investment portfolio within this area? The purpose of the study is to conduct a research that will provide investors with information about stock market correlation within the chosen market. We have conducted the study with a positivistic view and a deductive approach with some theories as our starting point. The main theories discussed are; market efficiency, risk and return, Modern Portfolio Theory, correlation and international investments. By using the financial datatbase, DataStream, we have been able to collect the necessary data for our study. The data has been processed in the statistical program SPSS by using Pearson correlation.