DOCSLIB.ORG

Mathematical Study of Free-Surface Fluids in Incompressible Dynamics Dena Kazerani

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mathematical Study of Free-Surface Fluids in Incompressible Dynamics Dena Kazerani Mathematical study of free-surface fluids in incompressible dynamics Dena Kazerani To cite this version: Dena Kazerani. Mathematical study of free-surface fluids in incompressible dynamics. Mathematics [math]. Université Pierre & Marie Curie - Paris 6, 2016. English. tel-01422881v2 HAL Id: tel-01422881 https://tel.archives-ouvertes.fr/tel-01422881v2 Submitted on 6 Feb 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Université Pierre et Marie Curie Laboratoire Jacques-Louis Lions Paris 6 UMR 7598 THÈSE DE DOCTORAT DE L’UNIVERSITÉ PIERRE ET MARIE CURIE Présentée et soutenue publiquement le 29 Novembre 2016 pour l’obtention du grade de DOCTEUR DE L’UNIVERSITÉ PIERRE ET MARIE CURIE Spécialité : Mathématiques Appliquées par Dena KAZERANI Études mathématiques de fluides à frontières libres en dynamique incompressible après avis des rapporteurs Roberto Natalini Consiglio Nazionale delle Ricerche (CNR) Fabio Nobile École Polytechnique Fédérale de Lausanne devant un jury composé de Vincent Duchêne Centre National de la Recherche Scientifique (CNRS) Examinateur Pascal Frey Université Pierre et Marie Curie-Paris 6 Directeur de thèse Edwige Godlewski Université Pierre et Marie Curie-Paris 6 Examinatrice Frédéric Legoll École des Ponts ParisTech Examinateur Fabio Nobile École Polytechnique Fédérale de Lausanne Rapporteur Jacques Sainte-Marie Centre d’études et d’expertise sur les risques, l’environnement, Examinateur la mobilité et l’aménagement (CEREMA) Nicolas Seguin Université de Rennes 1 Directeur de thèse École Doctorale de Sciences Mathématiques Faculté de Mathématiques de Paris Centre ED 386 UFR 929 Dena KAZERANI : Sorbonne Universités, UPMC Univ Paris 06, UMR 7598, Laboratoire Jacques-Louis Lions, F- 75005, Paris, France. CNRS, UMR 7598, Laboratoire Jacques-Louis Lions, F-75005, Paris, France. Adresse électronique: [email protected] 3 4 The test of a good teacher is not how many questions he can ask his pupils that they will answer readily, but how many questions he inspires them to ask him which he finds it hard to answer. Alice Wellington Rollins We are what we repeatedly do. Excellence then, is not an act, but a habit. Aristotle Remerciements Mes premiers remerciements s’adressent à mes directeurs de thèse, Pascal Frey et Nicolas Seguin. Je remercie Pascal pour m’avoir confié son code et m’avoir bénéficié de son expertise. Je lui suis particulièrement reconnaissante pour son soutien, sa compréhension et ses conseils. Je remercie de même, Nicolas Seguin pour m’avoir accordé sa confiance. J’ai été réellement impressionnée par son intuition, sa vision globale et sa vision stratège. Le contact simultané avec ces deux spécialistes m’a permis de bénéficier d’une formation pluridisciplinaire et enrichissante. Je suis très honorée que des personnalités scientifiques comme Roberto Natalini et Fabio No- bile acceptent de reporter cette thèse. Je remercie vivement Vincent Duchêne, Edwige Godlewski, Frédéric Legoll et Jacques Sainte-Marie pour avoir accepté de participer au jury. Le laboratoire Jacques-Louis Lions est un grand centre de recherche. Il est aussi riche sur le plan humain que sur le plan scientifique. Je remercie particulièrement Edwige Godlewski et Benoît Perthame de nous avoir donné l’occasion d’établir le concept du thé du LJLL. J’ai beaucoup appris pendant la période que j’ai passé dans ce laboratoire et ça c’est en grande partie, dû aux rencontres exceptionnelles que j’ai pu y faire. Je remercie Alain Haraux et Jean-Paul Penot pour les partages qu’ils m’ont accordés. J’estime avoir eu beaucoup de chance pour avoir été encadrée par Bruno Després pendant le stage de pré-M2. Il m’a généreusement montré la beauté et la richesse de la recherche en analyse numérique. La liste des gens qui ont indirectement contribué à la réalisation de cette thèse est exhaustive. Je remercie la gestion administrative et informatique du laboratoire. J’ai une pensée particulière envers les doctorants et anciens doctotrants du bureau 15-16-301 avec qui j’ai partagé des restaurants, des expositions et des cours de zumba. Je remercie aussi tous les doctorants/post-doctorants qui m’ont accompagné pour les déjeuners à la cantine, pour des pauses café et pour la gestion des bureaux des doctorants. De même, je remercie les doctorants que j’ai rencontrés pendant les conférences, pour les échanges, les balades et les courses à pied. Enfin, j’arrive à ceux dont la présence dépasse grandement le contexte de la thèse, ceux dont la présence chauffe mon coeur. Je pense à la personne à avoir cru le plus en mon intelligence: ma soeur Parna. Je pense aussi à mon père pour m’avoir fait comprendre entre autres que mes capacités étaient bien plus que ce que j’imaginais. Ma mère de son coté, n’a jamais cessé de me soutenir. C’est aussi grâce à eux que j’ai compris que le savoir n’est pas donné mais ça s’acquiert lentement, bout par bout. Mes derniers remerciements sont pour Alex, Archibald, Chiara, Dalila, Donya, Dounia, Flavien, François, Gazal, Géraldine, Jasmine, Hoel, Lara, Luiz, Maxime, Pato et Yiting. 5 6 Table of contents Introduction 9 1 Some results on a shallow water model called the Green-Naghdi equations . 10 2 Numerical simulation of the free surface incompressible Navier–Stokes equations . 29 I Some results on a shallow water model called the Green-Naghdi equations 35 1 The symmetric structure of Green–Naghdi type equations 37 1.1 Introduction . 37 1.2 Weak symmetric structure . 42 1.3 Application to Green–Naghdi type equations . 49 1.4 Conclusion . 56 1.A Computation of the second variation . 57 2 Global existence for small data of the viscous Green–Naghdi type equations 59 2.1 Introduction . 59 2.2 Main results . 64 2.3 A priori estimates . 68 2.4 Conclusion and Perspectives . 84 2.A Special Symmetric Structure . 85 2.B Local well-posedness . 87 2.C Linear stability of equilibriums of the Green-Naghdi equation . 88 II Numerical simulation of the free surface incompressible Navier–Stokes equa- 7 8 Table of contents tions 91 3 Numerical tools and global algorithm 93 3.1 Introduction . 93 3.2 Mathematical model . 95 3.3 Numerical tools . 97 3.4 Global numerical scheme . 112 3.5 Numerical results . 114 3.6 Conclusion and perspectives . 121 Bibliography 130 Introduction This thesis is about the mathematical study of free surface incompressible fluids. An incompressible flow is a fluid with a constant density. This implies a free divergence velocity. Obviously, water like most liquids is incompressible. In practice, if the density change of a fluid is small, it can be considered incompressible. This happens when the Mach number associated to the flow is low i.e. when the ratio of flow velocity to the speed of sound is small. Particularly, in our framework, air fits this regime and is considered incompressible. Incompressible fluids satisfy the incompressible Navier–Stokes equations: 8 ρ @u + (u · r)u − µ∆u + rp = ρf <> @t div u = 0 (0.1) > :u(0; x) = u0(x): Here ρ is the density whereas µ is the viscosity of the fluid. The unknowns of the problem are u the velocity flow and p the pressure. On the other hand, f is the density of force exerted on the fluid while u0 is the initial velocity flow. This equation is endowed with boundary conditions on the boundary of fluid domain. An incompressible fluid satisfying the Navier–Stokes equation (0.1) with a viscosity µ > 0, is called a Newtonian fluid. Nevertheless, if the Reynolds number associated to the flow i.e. the ratio of inertial forces to viscous forces is large, we can suppose that the fluid is perfect. In this case, it 9 10 1. Some results on a shallow water model called the Green-Naghdi equations satisfies the incompressible Euler equation (Navier–Stokes equation without the Laplace operator): 8 ρ @u + (u · r)u + rp = ρf <> @t div u = 0 (0.2) > :u(0; x) = u0(x): As an example, let us consider water. The viscosity of water is 0:001 P a:s while its density is 1000 kg=m3. Therefore, it is modeled by incompressible Euler equations in most applications specially in oceanography. For this reason, system (0.2) is the equation used in this latter domain, for the derivation of approximative models. These models are called shallow water and concern the regime where the fluid height is small compared to the characteristic wavelength. This regime coincides with the frame of some geophysical phenomena like tsunamis and earthquakes. Let us mention that in this work, our concern is the fluid’s free surface. Indeed, free surface flows satisfy the fluid equation on the fluid domain which moves following the velocity flow. For this reason, the treatment of the free surface raises some challenges which have led to the derivation of shallow water models and to creation of some specific numerical tools. The first part of the thesis is on the theoretical study of one of these approximative models called the Green–Naghdi equation whereas the second part is on the numerical study of System (0.1). 1 Some results on a shallow water model called the Green-Naghdi equations Shallow water models are essentially considered in Oceanography where the water height is small compared to the characteristic wavelength and the rotational effects are negligible.
Load more

Recommended publications
  • Fluid Mechanics
    FLUID MECHANICS PROF. DR. METİN GÜNER COMPILER ANKARA UNIVERSITY FACULTY OF AGRICULTURE DEPARTMENT OF AGRICULTURAL MACHINERY AND TECHNOLOGIES ENGINEERING 1 1. INTRODUCTION Mechanics is the oldest physical science that deals with both stationary and moving bodies under the influence of forces. Mechanics is divided into three groups: a) Mechanics of rigid bodies, b) Mechanics of deformable bodies, c) Fluid mechanics Fluid mechanics deals with the behavior of fluids at rest (fluid statics) or in motion (fluid dynamics), and the interaction of fluids with solids or other fluids at the boundaries (Fig.1.1.). Fluid mechanics is the branch of physics which involves the study of fluids (liquids, gases, and plasmas) and the forces on them. Fluid mechanics can be divided into two. a)Fluid Statics b)Fluid Dynamics Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at rest. It embraces the study of the conditions under which fluids are at rest in stable equilibrium Hydrostatics is fundamental to hydraulics, the engineering of equipment for storing, transporting and using fluids. Hydrostatics offers physical explanations for many phenomena of everyday life, such as why atmospheric pressure changes with altitude, why wood and oil float on water, and why the surface of water is always flat and horizontal whatever the shape of its container. Fluid dynamics is a subdiscipline of fluid mechanics that deals with fluid flow— the natural science of fluids (liquids and gases) in motion. It has several subdisciplines itself, including aerodynamics (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion).
    [Show full text]
  • Fluid Viscosity and the Attenuation of Surface Waves: a Derivation Based on Conservation of Energy
    INSTITUTE OF PHYSICS PUBLISHING EUROPEAN JOURNAL OF PHYSICS Eur. J. Phys. 25 (2004) 115–122 PII: S0143-0807(04)64480-1 Fluid viscosity and the attenuation of surface waves: a derivation based on conservation of energy FBehroozi Department of Physics, University of Northern Iowa, Cedar Falls, IA 50614, USA Received 9 June 2003 Published 25 November 2003 Online at stacks.iop.org/EJP/25/115 (DOI: 10.1088/0143-0807/25/1/014) Abstract More than a century ago, Stokes (1819–1903)pointed out that the attenuation of surface waves could be exploited to measure viscosity. This paper provides the link between fluid viscosity and the attenuation of surface waves by invoking the conservation of energy. First we calculate the power loss per unit area due to viscous dissipation. Next we calculate the power loss per unit area as manifested in the decay of the wave amplitude. By equating these two quantities, we derive the relationship between the fluid viscosity and the decay coefficient of the surface waves in a transparent way. 1. Introduction Surface tension and gravity govern the propagation of surface waves on fluids while viscosity determines the wave attenuation. In this paper we focus on the relation between viscosity and attenuation of surface waves. More than a century ago, Stokes (1819–1903) pointed out that the attenuation of surface waves could be exploited to measure viscosity [1]. Since then, the determination of viscosity from the damping of surface waves has receivedmuch attention [2–10], particularly because the method presents the possibility of measuring viscosity noninvasively. In his attempt to obtain the functionalrelationship between viscosity and wave attenuation, Stokes observed that the harmonic solutions obtained by solving the Laplace equation for the velocity potential in the absence of viscosity also satisfy the linearized Navier–Stokes equation [11].
    [Show full text]
  • Lecture 18 Ocean General Circulation Modeling
    Lecture 18 Ocean General Circulation Modeling 9.1 The equations of motion: Navier-Stokes The governing equations for a real fluid are the Navier-Stokes equations (con­ servation of linear momentum and mass mass) along with conservation of salt, conservation of heat (the first law of thermodynamics) and an equation of state. However, these equations support fast acoustic modes and involve nonlinearities in many terms that makes solving them both difficult and ex­ pensive and particularly ill suited for long time scale calculations. Instead we make a series of approximations to simplify the Navier-Stokes equations to yield the “primitive equations” which are the basis of most general circu­ lations models. In a rotating frame of reference and in the absence of sources and sinks of mass or salt the Navier-Stokes equations are @ �~v + �~v~v + 2�~ �~v + g�kˆ + p = ~ρ (9.1) t r · ^ r r · @ � + �~v = 0 (9.2) t r · @ �S + �S~v = 0 (9.3) t r · 1 @t �ζ + �ζ~v = ω (9.4) r · cpS r · F � = �(ζ; S; p) (9.5) Where � is the fluid density, ~v is the velocity, p is the pressure, S is the salinity and ζ is the potential temperature which add up to seven dependent variables. 115 12.950 Atmospheric and Oceanic Modeling, Spring '04 116 The constants are �~ the rotation vector of the sphere, g the gravitational acceleration and cp the specific heat capacity at constant pressure. ~ρ is the stress tensor and ω are non-advective heat fluxes (such as heat exchange across the sea-surface).F 9.2 Acoustic modes Notice that there is no prognostic equation for pressure, p, but there are two equations for density, �; one prognostic and one diagnostic.
    [Show full text]
  • Modelling Viscous Free Surface Flow
    Chapter 8 Modelling Viscous Free Surface Flow Free surface flows, where a boundary of a fluid body is free to move constrained only by forces across the surface, are possibly the most commonly observed flow phenomenon, with the motion of the free surface readily allowing the observation of flow of the fluid. Flows that are commonly encountered by the layperson include the motion of the surface of a river, the waves on the surface of the ocean, and the more personal flow of that in a cup of tea. From an engineering perspective, flows of interest include the open channel flow of rivers and canals, the erosive forces of waves on the shoreline, and the wakes generated by ships when under way. When modelling these flows, the problems associated with the solution of the Navier–Stokes equations are compounded by the free motion of the surface of the fluid, with the boundaries of the flow domain being a function of the flow structure, and thus an unknown which must be calculated along with the flow field. The movement of the free surface therefore both aids the observation of the flow, and hinders it’s modelling. In this chapter an attempt is made to model the steady flow around a ships hull. The modelling of such a flow is of great interest to Naval Architects, with the ability to predict the resistance of ships allowing the design of more efficient hull forms, whilst the accurate modelling of the ships wake allows the design of hulls that create a smaller disturbance in confined waterways.
    [Show full text]
  • A Simple and Unified Linear Solver for Free-Surface and Pressurized
    water Technical Note A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems Dechao Hu 1 , Songping Li 1, Shiming Yao 2 and Zhongwu Jin 2,* 1 School of Hydropower and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; [email protected] (D.H.); [email protected] (S.L.) 2 Yangtze River Scientific Research Institute, Wuhan 430010, China; [email protected] * Correspondence: [email protected]; Tel.: +86-027-8282-9873 Received: 19 August 2019; Accepted: 19 September 2019; Published: 23 September 2019 Abstract: A semi–implicit numerical model with a linear solver is proposed for the free-surface and pressurized mixed flows in hydraulic systems. It solves the two flow regimes within a unified formulation, and is much simpler than existing similar models for mixed flows. Using a local linearization and an Eulerian–Lagrangian method, the new model only needs to solve a tridiagonal linear system (arising from velocity-pressure coupling) and is free of iterations. The model is tested using various types of mixed flows, where the simulation results agree with analytical solutions, experiment data and the results reported by former researchers. Sensitivity studies of grid scales and time steps are both performed, where a common grid scale provides grid-independent results and a common time step provides time-step-independent results. Moreover, the model is revealed to achieve stable and accurate simulations at large time steps for which the CFL is greater than 1. In simulations of a challenging case (mixed flows characterized by frequent flow-regime conversions and a closed pipe with wide-top cross-sections), an artificial slot (A-slot) technique is proposed to cope with possible instabilities related to the discontinuous main-diagonal coefficients of the linear system.
    [Show full text]
  • 2.016 Hydrodynamics Free Surface Water Waves
    2.016 Hydrodynamics Reading #7 2.016 Hydrodynamics Prof. A.H. Techet Fall 2005 Free Surface Water Waves I. Problem setup 1. Free surface water wave problem. In order to determine an exact equation for the problem of free surface gravity waves we will assume potential theory (ideal flow) and ignore the effects of viscosity. Waves in the ocean are not typically uni-directional, but often approach structures from many directions. This complicates the problem of free surface wave analysis, but can be overcome through a series of assumptions. To setup the exact solution to the free surface gravity wave problem we first specify our unknowns: • Velocity Field: V (x, y, z,t ) = ∇φ(x, y, z,t ) • Free surface elevation: η(x, yt, ) • Pressure field: p(xy,,z , t ) version 3.0 updated 8/30/2005 -1- ©2005 A. Techet 2.016 Hydrodynamics Reading #7 Next we need to set up the equations and conditions that govern the problem: • Continuity (Conservation of Mass): ∇=2φ 0 for z <η (Laplace’s Equation) (7.1) • Bernoulli’s Equation (given some φ ): 2 ∂φ 1 pp− a ∂t +∇2 φ + ρ + gz = 0 for z <η (7.2) • No disturbance far away: ∂φ ∂t , ∇→φ 0 and p = pa − ρ gz (7.3) Finally we need to dictate the boundary conditions at the free surface, seafloor and on any body in the water: (1) Pressure is constant across the free surface interface: p = patm on z =η . ⎧∂φ 1 2 ⎫ p =−ρ ⎨ − V − gz⎬ + c ()t= patm . (7.4) ⎩ ∂t 2 ⎭ Choosing a suitable integration constant, ct( ) = patm , the boundary condition on z =η becomes ∂φ 1 ρ{ + V 2 + gη} = 0.
    [Show full text]
  • PRESSURE 68 Kg 136 Kg Pressure: a Normal Force Exerted by a Fluid Per Unit Area
    CLASS Second Unit PRESSURE 68 kg 136 kg Pressure: A normal force exerted by a fluid per unit area 2 Afeet=300cm 0.23 kgf/cm2 0.46 kgf/cm2 P=68/300=0.23 kgf/cm2 The normal stress (or “pressure”) on the feet of a chubby person is much greater than on the feet of a slim person. Some basic pressure 2 gages. • Absolute pressure: The actual pressure at a given position. It is measured relative to absolute vacuum (i.e., absolute zero pressure). • Gage pressure: The difference between the absolute pressure and the local atmospheric pressure. Most pressure-measuring devices are calibrated to read zero in the atmosphere, and so they indicate gage pressure. • Vacuum pressures: Pressures below atmospheric pressure. Throughout this text, the pressure P will denote absolute pressure unless specified otherwise. 3 Other Pressure Measurement Devices • Bourdon tube: Consists of a hollow metal tube bent like a hook whose end is closed and connected to a dial indicator needle. • Pressure transducers: Use various techniques to convert the pressure effect to an electrical effect such as a change in voltage, resistance, or capacitance. • Pressure transducers are smaller and faster, and they can be more sensitive, reliable, and precise than their mechanical counterparts. • Strain-gage pressure transducers: Work by having a diaphragm deflect between two chambers open to the pressure inputs. • Piezoelectric transducers: Also called solid- state pressure transducers, work on the principle that an electric potential is generated in a crystalline substance when it is subjected to mechanical pressure. Various types of Bourdon tubes used to measure pressure.
    [Show full text]
  • On the Generation of Vorticity at a Free-Surface
    Center for TurbulenceResearch Annual Research Briefs On the generation of vorticity at a freesurface By T Lundgren AND P Koumoutsakos Motivations and ob jectives In free surface ows there are many situations where vorticityenters a owin the form of a shear layer This o ccurs at regions of high surface curvature and sup ercially resembles separation of a b oundary layer at a solid b oundary corner but in the free surface ow there is very little b oundary layer vorticity upstream of the corner and the vorticity whichenters the owisentirely created at the corner Ro o d has asso ciated the ux of vorticityinto the ow with the deceleration ofalayer of uid near the surface These eects are quite clearly seen in spilling breaker ows studied by Duncan Philomin Lin Ro ckwell and Dabiri Gharib In this pap er we prop ose a description of free surface viscous ows in a vortex dynamics formulation In the vortex dynamics approach to uid dynamics the emphasis is on the vorticityvector which is treated as the primary variable the velo city is expressed as a functional of the vorticity through the BiotSavart integral In free surface viscous ows the surface app ears as a source or sink of vorticityand a suitable pro cedure is required to handle this as a vorticity b oundary condition As a conceptually attractivebypro duct of this study we nd that vorticityis conserved if one considers the vortex sheet at the free surface to contain surface vorticity Vorticity which uxes out of the uid and app ears to b e lost is really gained by the vortex sheet
    [Show full text]
  • Pressure and Fluid Statics
    cen72367_ch03.qxd 10/29/04 2:21 PM Page 65 CHAPTER PRESSURE AND 3 FLUID STATICS his chapter deals with forces applied by fluids at rest or in rigid-body motion. The fluid property responsible for those forces is pressure, OBJECTIVES Twhich is a normal force exerted by a fluid per unit area. We start this When you finish reading this chapter, you chapter with a detailed discussion of pressure, including absolute and gage should be able to pressures, the pressure at a point, the variation of pressure with depth in a I Determine the variation of gravitational field, the manometer, the barometer, and pressure measure- pressure in a fluid at rest ment devices. This is followed by a discussion of the hydrostatic forces I Calculate the forces exerted by a applied on submerged bodies with plane or curved surfaces. We then con- fluid at rest on plane or curved submerged surfaces sider the buoyant force applied by fluids on submerged or floating bodies, and discuss the stability of such bodies. Finally, we apply Newton’s second I Analyze the rigid-body motion of fluids in containers during linear law of motion to a body of fluid in motion that acts as a rigid body and ana- acceleration or rotation lyze the variation of pressure in fluids that undergo linear acceleration and in rotating containers. This chapter makes extensive use of force balances for bodies in static equilibrium, and it will be helpful if the relevant topics from statics are first reviewed. 65 cen72367_ch03.qxd 10/29/04 2:21 PM Page 66 66 FLUID MECHANICS 3–1 I PRESSURE Pressure is defined as a normal force exerted by a fluid per unit area.
    [Show full text]
  • Boundary Conditions in Fluid Mechanics
    Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University, Potsdam, New York 13699 The governing equations for the velocity and pressure fields are partial differential equations that are applicable at every point in a fluid that is being modeled as a continuum. When they are integrated in any given situation, we can expect to see arbitrary functions or constants appear in the solution. To evaluate these, we need additional statements about the velocity field and possibly its gradient at the natural boundaries of the flow domain. Such statements are known as boundary conditions. Usually, the specification of the pressure at one point in the system suffices to establish the pressure fields so that we shall only discuss boundary conditions on the velocity field here. For a more detailed discussion of various aspects, the reader is encouraged to consult either Leal (1) or Batchelor (2). Conditions at a rigid boundary It is convenient for the purpose of discussion to identify two types of boundaries. One is that at the interface between a fluid and a rigid surface. At such a surface, we shall require that the tangential component of the velocity of the fluid be the same as the tangential component of the velocity of the surface, and similarly the normal component of the velocity of the fluid be the same as the normal component of the velocity of the surface. The former is known as the “no slip” boundary condition, and has been found to be successful in describing most practical situations. It was a subject of controversy in the eighteenth and nineteenth centuries, and was finally accepted because predictions based on assuming it were found to be consistent with observations of macroscopic quantities such as the flow rate through a circular capillary under a given pressure drop.
    [Show full text]
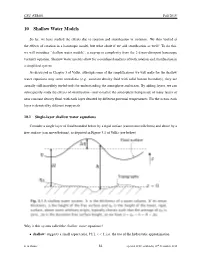
  • 10 Shallow Water Models
    CSU ATS601 Fall 2015 10 Shallow Water Models So far, we have studied the effects due to rotation and stratification in isolation. We then looked at the effects of rotation in a barotropic model, but what about if we add stratification as well? To do this, we will introduce “shallow water models”, a step-up in complexity from the 2-d non-divergent barotropic vorticity equation. Shallow water models allow for a combined analysis of both rotation and stratification in a simplified system. As discussed in Chapter 3 of Vallis, although some of the simplifications we will make for the shallow water equations may seem unrealistic (e.g. constant density fluid with solid bottom boundary), they are 5 Shallowactually still incredibly Water useful tools Models for understanding the atmosphere and ocean. By adding layers, we can So far wesubsequently have studied study the the effects eff ofects stratification due to - rotation and visualize (chapter the atmosphere 3) and being stratification made of many layers (chapter of 4) in isolation.near constant Shallow density water fluid,with models each layer allow denoted for a by combined different potential analysis temperatures. of both For eff theects ocean, in eacha highly simplifiedlayer system. is denoted They by different are very isopycnals. powerful in providing fundamental dynamical insight. 5.1 Introduction,10.1 Single-layer shallow Single water Layer equations[Vallis 3.1] Consider a single layer of fluid bounded below by a rigid surface and above by a free surface, Consider a single layer of fluid bounded below by a rigid surface (cannot move/deform) and above by a as depicted below (taken from Vallis, see figure caption for description of variables).
    [Show full text]
  • Chapter 11 Flow with Free Surface
    Chapter 11 Flow with Free Surface We have already encountered free surfaces in systems such as the drainage of a liquid along a wall. In this case the free surface was a material surface and the boundary condition was that of continuity of pressure and shear stress. The same boundary conditions would be used for wind-driven waves on water and the shape of the vortex formed when water drains from a bathtub. The dimensionless numbers of importance are the Reynolds number NULRe = ρ / μ , 2 2 ρ gL NRe Froude number NUgFr = / L, and gravity number NG ==. These μUNFr mentioned systems are of a macroscopic scale compared to surface forces and rheology and thus surface tension, surface elasticity, and surface viscosity were not significant. However, when the system dimensions become about 1 cm or less surface forces are no longer negligible and play an important role in the shape of the interface and in transport processes. The capillary number 2 NUCa = μ /σ and Bond number NgLBo = ρ /σ introduced in Chapter 6 become important dimensionless groups that quantify the ratio of viscous/capillary and gravity/capillary forces. As the dimensions decrease to about 1 mm we are in the range of capillary phenomena where surface tension and contact angles become important (e.g., the rise of a wetting liquid in a small capillary). As the dimensions decrease to 1 μm we are in the colloidal regime and not only is capillarity a dominant effect but also particles have spontaneous motion due to Brownian motion and thin films display optical interference as in the color of soap films.
    [Show full text]