DOCSLIB.ORG

Phase Jump Due to Partial Reflection of Irregular Water Waves at Steep Slopes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Phase Jump Due to Partial Reflection of Irregular Water Waves at Steep Slopes Phase Jump due to Partial Reflection of Irregular Water Waves at Steep Slopes Supplement to: „Wave Resonances Detected in a Wave Tank and in the Field“, 5th Int. Symposium WAVES 2005, Madrid, Spain, Paper 134 Prof. Dr.-Ing. Fritz Büsching Bielefeld University of Applied Sciences Fluid Dynamics Laboratory Minden, Germany urn:nbn:de:0066-201011165 http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 1/25 Scope of Presentation • Statement: The process of wavewave breakingbreaking at slopes ≤ n ≤ 2:1:13:1 is inextricably linked with the simultaneoussimultaneous formationformation of a reflectedreflected wavewave andand aa wavewave ofof transmissiontransmission. Superimposition of incident and reflected waves results in the formation of a partialpartial clapotisclapotis comprising of a phase jump. • Analogue: Fresnel´s Equations describing reflectionreflection andand transmissiontransmission of light at uniform planar interfaces. • http://www.digibib.tu-bs.de/?docid=00047044Reflection coefficientsCoastlab 2010, BarcelonaCr = f(Hr/Hi, Δφ0/IV19/08/2014)< 2/250. Partial standing waves breaking on a slope with reference to the point IP of the still water level intersecting the slope Main topic: Influence of a phase shift Δϕ on breakers interacting with sloping structures Slopes Damping ≤ n ≤ 2:1:13:1 Structure SWL IP d = 0.626m Wave Maker With and without re-Reflection 0.79m 1.79m Measurements of water level deflections quasi synchronously at 91 wave probe stations equally spaced 10 cm. http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 3/25 Tests on the stability of Hollow Cubes Δx Model scale: 1:5 Slopes: 1 : 3≤ 1n :≤ 1 : 2 Wave heights up to H = 0.35m Punging breaker on Collapsing breaker on xΔ 0≈ . 15 m quasi Smooth Slope Hollow Cubes Cr = -0.32 Cr = -0.16 http://www.digibib.tu-bs.de/?docid=00047044 abCoastl ona2010, Barcel 19/08/2014 4/25 Maximum run up Differences: Δy • extent • phase yΔ 0≈ . 40 m Run down of collapsing Run down of plunging breaker on Hollow Cubes breaker on Smooth Slope http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 5/25 Energy Density Spectra of Water Level Deflections (Composite Power Spectra) ~IA ~IA 256 Components Δf = 0.00543 Hz cut off cut off cut off cut off Permeable revetment Plane revetment (measured synchronously) http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 6/25 Energy lines resulting from 256 frequency components total frequency range 0.0326 – 1.3997 Hz IA(p x Hz) (resultant clapotis length) Emin 256 Components Δf = 0.00543 Hz Slope 1:3 http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 7/25 General properties of partial standing waves at a slope Breakers Partial Clapotis Envelopes Envelopes Partial Clapotis Energy Potential energy EE− E = maximum energy at loop i Reflection max,i min,i max,i Cr, i = where and coefficient EEmax,i + min,i Emin,i = minimum energy at node i http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 8/25 Energy lines of 12 definable partial clapotis waves frequency range 0.4015 – 0.8030 Hz (74 components) Subfrequency ranges of 0.014 ≤ n.Δf ≤ 0.085 Hz Slope 1:3 http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 9/25 12 partial standing waves at slope 1:m = 1:3 Minimum partial clapotis node distances from IP IP http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 10/25 Modified data procession and presentation for slopes 1:2 Hollow Cubes piled up to form a stepped face hollow seawall structure (2-layer-system). Slope: 1:2 Model scale: 1:10 Hollow Cubes with the stem C = +0.2 placed at one r bottom edge http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 11/25 Modified data procession and presentation for slopes 1:2 Comments: cut off noise frequencies • At steeper slope 1:2 measurements closer to IP. • Set of partial clapotis IP waves identifiable, although re-reflection effect prevented. • Energy contents of partial clapotis waves cut off noise piled up with reference frequencies to gauge station numbers Close to IP • nodes at smooth slope and IP • loops at hollow slope. http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 12/25 Monochromatic waves at smooth slopes: NODE DISTANCE FROM STRUCTURE Relative node distances a/LSMOOTH with SLOPESreference to slope angle a/L 0,25-0,3 0.25 0,2-0,25 0,15-0,2 0.20 0,1-0,15 0,05-0,1 0.15 0-0,05 0.10 -0,05-0 -0,1--0,05 0.05 a/L 0.00 IP -0.05 0,30 .450 0,25 .529 0,20 0,15 .625 FREQUENCY [Hz] 0,10 0,05 .766 ≤ ≤ 22.217.1 sT IP 0,00 .800 -0,05 -0,10 .853 90,00 84,29 63,43 45,00 26,56 18,43 Joint trends: o SLOPE ANGLE [ ] Nodes closer to IP with tanα = 1:m 1:0.1 1:0.5 1:1 1:2 1:3 • slope angle decreasing • frequency increasing http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 13/25 Two kinds of standing transversal waves (without transmission) Free end reflection without phase jump (shift) (wave crest reflectet by wave crest) Known examples: • Rope waves • Electromagnetic waves • Water waves (Clapotis) Fixed end reflection with phase jump Δϕ = 180o (wave crest reflectet by wave trough & vice versa) Known examples: • Rope waves • Electromagnetic waves • Water waves (at a slope?) incident wave: red reflected wave: blue resultant wave: black Click on the figure to start animation Animations after Walter Fendt (2003) http://www.walter-fendt.de/ph14d/stwellerefl.htm http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 14/25 Wave breaking combined with partial reflection and transmission (wave moving to the left) Partial Clapotis Runup Node Loop Node 1 4 2 3 6 Runup = transmitted IP 5 wave pulse (phase 4) Breaking wave • The existence of a node close to the slope provides evidence of partial reflection with a phase jump . • Note opposite transmitted and reflected deflections around IP. • Conservation of momentum: Smaller & slower transmitted wave pulse ct < ci combined with negative reflection (wave crest reflected by wave trough & vv) http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 15/25 Wave breaking combined with partial reflection and transmission (wave moving to the left) Runup = transmitted wave pulse (phase 4) Breaking wave Click on the figure to start animation • The existence of a node close to the slope provides evidence of partial reflection with a phase jump . • Note opposite transmitted and reflected deflections around IP. • Conservation of momentum: Smaller & slower transmitted wave pulse ct < ci combined with negative reflection (wave crest reflectet by wave trough & vv) http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 16/25 AnalogueAnalogue fromfrom ropelight waves: waves: Fresnel´s Equations describing reflection and transmission of light at uniform planar interfaces Interface of two refractive index media Partial reflection and lower higher transmission of a pulse travelling to the right from low to high refractive index medium. Superimposition of positive incident and negative reflected pulses not shown ! Animation after Oleg Alexandrow (2007) ci cr ct < ci http://de.wikipedia.org/wiki/Datei/:Partial_transmittance.gif breaking Click on the figure to start animation wave Incident and transmitted Analogue behaviour of water reflected pulse pulse = runup waves breaking on a slope respectively (except rundown). negative partial reflection http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 17/25 Analogue from rope waves: Partial reflection and transmission of a puls travelling to the right from thinner to thicker rope diameter. Boundary of two ropes thinner thicker incident pulse: white reflected pulse: red transmitted pulse: blue Superimposition of positive incident and negative reflected pulse not shown ! Animations after B. Surendranath Reddy (2004) http://www.surendranath.org/Apps.html cr = ci ct < ci Click on the figure to start animation breaking incident and wave transmitted Analogue behaviour of water reflected pulse pulse = runup waves breaking on a slope respectively (except rundown). negative partial reflection http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 18/25 Further considerations on the positioning of partial standing waves with reference to a sloping structure http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 19/25 Consequences of phase shifts on reflection coefficients Wave height ratio: Hr / Hi = 1.0 < 4.00 > 0 http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 20/25 Consequences of phase shifts on reflection coefficients Wave height ratio: Hr / Hi = 0.7 < 3.4 > 0.6 http://www.digibib.tu-bs.de/?docid=00047044 Coastlab 2010, Barcelona 19/08/2014 21/25 Consequences of a phase shift on reflection coefficients Partial Clapotis Envelopes Loop Loop Node Node Node envelopeWave crest Wave trough envelope Hmin L/4 L/4 Hmax ? L (by HReflection Coefficient ealy, 1953): H r HHmax − min Wave C = = whereHHHmax = i+ r andHHHmin = i− r r ratioheight H i HHmax + min Phase shift ⎛ H π ⎞ HH− 3 . 14− 1 . 42 C=f ⎜ r =0 . 7 Δϕ , =⎟ = max min = 0= . 377 considered r ⎜ ⎟ ⎝ H i 4 ⎠ HHmax + 3min . 14+ 1 . 42 http://www.digibib.tu-bs.de/?docid=00047044 abCoastl ona2010, Barcel 19/08/2014 22/25 rof parametersin the ange coefficients Reflection 0 .
Load more

Recommended publications
  • Waves and Structures
    WAVES AND STRUCTURES By Dr M C Deo Professor of Civil Engineering Indian Institute of Technology Bombay Powai, Mumbai 400 076 Contact: [email protected]; (+91) 22 2572 2377 (Please refer as follows, if you use any part of this book: Deo M C (2013): Waves and Structures, http://www.civil.iitb.ac.in/~mcdeo/waves.html) (Suggestions to improve/modify contents are welcome) 1 Content Chapter 1: Introduction 4 Chapter 2: Wave Theories 18 Chapter 3: Random Waves 47 Chapter 4: Wave Propagation 80 Chapter 5: Numerical Modeling of Waves 110 Chapter 6: Design Water Depth 115 Chapter 7: Wave Forces on Shore-Based Structures 132 Chapter 8: Wave Force On Small Diameter Members 150 Chapter 9: Maximum Wave Force on the Entire Structure 173 Chapter 10: Wave Forces on Large Diameter Members 187 Chapter 11: Spectral and Statistical Analysis of Wave Forces 209 Chapter 12: Wave Run Up 221 Chapter 13: Pipeline Hydrodynamics 234 Chapter 14: Statics of Floating Bodies 241 Chapter 15: Vibrations 268 Chapter 16: Motions of Freely Floating Bodies 283 Chapter 17: Motion Response of Compliant Structures 315 2 Notations 338 References 342 3 CHAPTER 1 INTRODUCTION 1.1 Introduction The knowledge of magnitude and behavior of ocean waves at site is an essential prerequisite for almost all activities in the ocean including planning, design, construction and operation related to harbor, coastal and structures. The waves of major concern to a harbor engineer are generated by the action of wind. The wind creates a disturbance in the sea which is restored to its calm equilibrium position by the action of gravity and hence resulting waves are called wind generated gravity waves.
    [Show full text]
  • Nearshore Current Pattern and Rip Current Occurrence at Jungmun Beach, Jeju by Numerical Computation 1. Introduction
    한국항해항만학회지 제41권 제2호 J. Navig. Port Res. Vol. 41, No. 2 : 55-62, April 2017 (ISSN:1598-5725(Print)/ISSN:2093-8470(Online)) DOI : http://dx.doi.org/10.5394/KINPR.2017.41.2.55 Nearshore Current Pattern and Rip Current Occurrence at Jungmun Beach, Jeju by Numerical Computation Seung-Hyun An*․†Nam-Hyeong Kim *Coastal, Harbor and Disaster Prevention Research Institute, Sekwang Engineering Consultants Co., LTD. †Department of Civil Engineering, J eju National University, Jeju 63243, Korea Abstract : A nearshore current or a wave-induced current is an important phenomenon in a nearshore zone, which is composed of longshore, cross-shore, and rip currents. The nearshore current is closely related to the occurrence of coastal accidents by beachgoers. A considerable number of coastal accidents by beachgoers involving the rip current have been reported at Jungmun Beach. However, in studies and observations of the nearshore current of Jungmun Beach, understanding of the rip current pattern remains unclear. In this study, a scientific approach is taken to understand the nearshore current and the rip current patterns at Jungmun Beach by numerical computation for year of 2015. From results of numerical computation, the occurrence and spatial characteristics of the rip current, and the similarities between the rip current and incident wave conditions are analyzed. The primary results of this study reveal that the rip currents are frequently generated at Jungmun Beach, especially in the western parts of the beach, and that the rip currents often occur with a wave breaking height of around 0.5 ~ 0.7 m, a wave period of around 6 ~ 8 seconds, and a breaking angle of around 0 ~ 15 degrees.
    [Show full text]
  • Beach Accretion with Erosive Waves : "Beachbuilding" Accrétion Sur Les Plages Avec Vagues Érosives : "La Technique De Construction De Plage "
    Beach accretion with erosive waves : "Beachbuilding" Accrétion sur les plages avec vagues érosives : "la technique de construction de plage " Melville W. BEARDSLEY US Army Corps of Engineers, Beachbuilder Company Roger H. CHARLIER HAECON Inc., Free University of BRUSSELS - Belgique Abstract : A new method of beach preservation, theBeachbuilder Technique , proposes to harness the energy of normally erosive waves to produce beach accretion. A "flow control sheet" located in the surf zone directs the flow of swash and backwash causing net transport of sediment onto the beach. Beach and surf zone profiles created by the wave-tank tests show that the technique leads to accretion on this beach, during every test run with erosive waves. The successful wave tank results should reproduce on actual beaches ; rapid accretion on real beaches can be expected from the scaled wave-tank results. It is anticipated that by use of this new technique, costs of beach preservation would be cut by as much as 66%. Furthermore, rapid beach accretion, quick reaction, high mobility, good durability, «nd provision of employment for making the installations are major benefits to be derived. K e y w o rd s . Erosion - Waves - Accretion - Nourishment - Beach Résum é : Une nouvelle méthode de protection de plages, Techniquela de Construction de Plage, est proposée. Un "drap de contrôle d’écoulement" placé dans la zone des brisants dirige le clapotis et le remous et provoque un transport de sédiment vers la plage. Les profils de plage et de brisants créés par des tests conduits en bassins montrent que la technique produit une accumulation sur la plage pendant chaque test avec vagues érosives.
    [Show full text]
  • Air-Sea Interactions - Jacques C.J
    OCEANOGRAPHY – Vol.I - Air-Sea Interactions - Jacques C.J. Nihoul and François C. Ronday AIR-SEA INTERACTIONS Jacques C.J. Nihoul and François C. Ronday University of Liège, Belgium Keywords: Wind waves, fully developed sea, tsunamis, swell, clapotis, seiches, littoral current, rip current, air-sea interactions, sea slicks, drag coefficient. Contents 1. Introduction 2. Wind waves 3. Air-Sea Interactions Glossary Bibliography Biographical Sketches Summary The marine system is part of the general geophysical system. Physical and chemical boundary interactions at the air-sea interface are essential factors in the marine system's dynamics Wind blowing over the sea generates surface waves and energy is transferred from the wind to the ocean's upper layer. The fluxes of the momentum, heat, chemicals... at the air-sea interface are usually parameterized by bulk formula which assumed that the fluxes are proportional to the magnitude of the wind velocity at some reference height (10m, say). Although these bulk formulas have abundantly been used in several generations of models, they can only give a rough representation of the mechanisms of air-sea interactions where wave’s field’s characteristics, bubbles and spray, surface slicks, heavy rainfalls...can play a significant role. 1. Introduction Incoming short wave solar radiation and outgoing long wave radiation emitted by the earth surface, mediated by back and forth long wave emissions by clouds and aerosols - with its spatial variability due, in particular, to the earth’s sphericity - constitute
    [Show full text]
  • Two-Dimensional Wave-Making Problem C.R. Chou, R.S. Shih, J.Z. Yim Department of Harbor and River Engineering, National Taiwan O
    Transactions on Modelling and Simulation vol 12, © 1996 WIT Press, www.witpress.com, ISSN 1743-355X Two-dimensional wave-making problem C.R. Chou, R.S. Shih, J.Z. Yim Department of Harbor and River Engineering, National Taiwan Ocean University, Bee-Ning Road 2, Keelung 202, Taiwan Abstract In this study, generation of two dimensional nonlinear waves is simulated numerically using boundary clement method. The present scheme is based on a Lagrangian description together with finite differencing of the time step. An algorithm to generate waves with any prescribed form is also implantec in the scheme. The numerical model was first verified by studying the case of finite amplitude waves impinging against a vertical wall. Time histories of evolution of a soliton running up on a sloping beach, as well as over a submerged obstacle are then presented. 1 Introduction Problems associated with generation, propagation and deformatio.i have been studied numerically by many researchers. Based on a mixed Eulerian- Lagrangian method, solitary wave interacting with a gentle slope, and wave breaking on water of gradually varying depth are simulated numerically in two- dimensional fluid region by Sujjino and Tosaka[l], Ouyama[2] explored soli- tary wave set up on a slope by boundary element method. Pedersen & Gjevik[3 ] developed a numerical model to study run-up of long waves governed by a set of Boussinesq equations. Lagrangian coordinate description was used to sim- plify the numerical treatment of a moving shoreline. Based on the Green';* formular, Nakayama[4] applied a new boundary element technique to analyze nonlinear water wave problems.
    [Show full text]
  • Title on the Effect of Wind on Wave Overtopping on Vertical Seawalls Author(S)
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Kyoto University Research Information Repository On the Effect of Wind on Wave Overtopping on Vertical Title Seawalls Author(s) IWAGAKI, Yuichi; TSUCHIYA, Yoshito; INOUE, Masao Bulletin of the Disaster Prevention Research Institute (1966), Citation 16(1): 11-30 Issue Date 1966-09 URL http://hdl.handle.net/2433/124717 Right Type Departmental Bulletin Paper Textversion publisher Kyoto University Bull. Disas. Prey. Res. Inst. Kyoto Univ., Vol. 16, Part 1, No. 105, Sept., 1965 On the Effect of Wind on Wave Overtopping on Vertical Seawalls By Yuichi IWAGAKI, Yoshito TSUCHIYA and Masao INOUE (Manuscript received June 30. 1966) Synopsis In designing seawalls and seadikes, it is very important to estimate the quantity of wave overtopping on them as exactly as possible. The estimation, however, is difficult because of complicated phenomenaof wave overtopping, and in particular the effect of wind on wave overtopping is entirely unknown. With this in view, the authors have begun the study to disclose the effect of wind on wave overtopping quantitatively. As a first step of the study. the present paper describes some experimental results of wave overtoppingon vertical seawalls for the wave steepnesses of 0.01 and 0.02, accompanied with wind created by a high-speed wind-wave tunnel, which is 0.8 m wide. 2.3m to 4.0 m high and 40 m long, having a blower of 100HP and a wave generator of submerged piston type with a motor of 10 HP. The main results obtained from the experiments are summarized as follows.
    [Show full text]
  • Chapter 31 WAVE FORCES AGAINST SEA WALL Masashi Hom-Ma and Kiyoshi Horikawa Department of Civil Engineering, University of Tokyo
    Chapter 31 WAVE FORCES AGAINST SEA WALL Masashi Hom-ma and Kiyoshi Horikawa Department of Civil Engineering, University of Tokyo Tokyo, Japan INTRODUCTION The study concerning the wave forces acting on breakwater has been conducted by numerous scientists and engineers both in field and in laboratory,, While few studies have been car- ried out on the wave forces acting on sea wall which is located inside the surf zone. In this paper are summarized the main results of the experimental studies conducted at the University of Tokyo, Japan, in relation to the subject on the wave forces against a vertical or inclined surface wall located shorewards from the breaking point, and also is proposed an empirical formula of wave pressure distribution on a sea wall on the basis of the experimental data. The computed results obtained by using the above formula are compared with the field data of wave pressure on a vertical wall measured at the Niigata West Coast, Niigata Prefecture, Japan, and also with the experimen- tal data of total wave forces on a vertical wall; the project of the latter is now in progress at the University of Tokyo, PRESENTATION OP EXPERIMENTAL RESULTS LABORATORY PROCEDURES The wave channel which is used for the present studies is 18 m long, 0.6 m high and 0.7 m wide, and a model of sea wall is installed on a gentle uniform slope of l/l5. The face angle of the model is adjustable in a wide range, and six pres- sure gauges are attached on the surface of model sea wall at different levels to measure simultaneously the time history of pressure workxng on a sea wall.
    [Show full text]
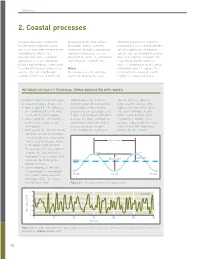
  • 2. Coastal Processes
    CHAPTER 2 2. Coastal processes Coastal landscapes result from by weakening the rock surface and driving nearshore sediment the interaction between coastal to facilitate further sediment transport processes. Wind and tides processes and sediment movement. movement. Biological, biophysical are also significant contributors, Hydrodynamic (waves, tides and biochemical processes are and are indeed dominant in coastal and currents) and aerodynamic important in coral reef, salt marsh dune and estuarine environments, (wind) processes are important. and mangrove environments. respectively, but the action of Weathering contributes significantly waves is dominant in most settings. to sediment transport along rocky Waves Information Box 2.1 explains the coasts, either directly through Ocean waves are the principal technical terms associated with solution of minerals, or indirectly agents for shaping the coast regular (or sinusoidal) waves. INFORMATION BOX 2.1 TECHNICAL TERMS ASSOCIATED WITH WAVES Important characteristics of regular, Natural waves are, however, wave height (Hs), which is or sinusoidal, waves (Figure 2.1). highly irregular (not sinusoidal), defined as the average of the • wave height (H) – the difference and a range of wave heights highest one-third of the waves. in elevation between the wave and periods are usually present The significant wave height crest and the wave trough (Figure 2.2), making it difficult to off the coast of south-west • wave length (L) – the distance describe the wave conditions in England, for example, is, on between successive crests quantitative terms. One way of average, 1.5m, despite the area (or troughs) measuring variable height experiencing 10m-high waves • wave period (T) – the time from is to calculate the significant during extreme storms.
    [Show full text]
  • Second-Order Time-Dependent Mild-Slope Equation for Wave Transformation
    Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 2014, Article ID 341385, 15 pages http://dx.doi.org/10.1155/2014/341385 Research Article Second-Order Time-Dependent Mild-Slope Equation for Wave Transformation Ching-Piao Tsai,1 Hong-Bin Chen,2 and John R. C. Hsu3,4 1 Department of Civil Engineering, National Chung Hsing University, Taichung 402, Taiwan 2 Department of Leisure and Recreation Management, Chihlee Institute of Technology, New Taipei 220, Taiwan 3 Department of Marine Environment & Engineering, National Sun Yat-Sen University, Kaohsiung 804, Taiwan 4 School of Civil & Resources Engineering, University of Western Australia, Crawley, WA 6009, Australia Correspondence should be addressed to Ching-Piao Tsai; [email protected] Received 16 October 2013; Accepted 1 May 2014; Published 4 May 2014 Academic Editor: Efstratios Tzirtzilakis Copyright © 2014 Ching-Piao Tsai et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. This study is to propose a wave model with both wave dispersivity and nonlinearity for the wave field without water depth restriction. A narrow-banded sea state centred around a certain dominant wave frequency is considered for applications in coastal engineering. A system of fully nonlinear governing equations is first derived by depth integration of the incompressible Navier-Stokes equation in conservative form. A set of second-order nonlinear time-dependent mild-slope equations is then developed by a perturbation scheme. The present nonlinear equations can be simplified to the linear time-dependent mild-slope equation, nonlinear longwave equation, and traditional Boussinesq wave equation, respectively.
    [Show full text]
  • The Water Waves Problem Mathematical Analysis and Asymptotics
    Mathematical Surveys and Monographs Volume 188 The Water Waves Problem Mathematical Analysis and Asymptotics David Lannes American Mathematical Society http://dx.doi.org/10.1090/surv/188 The Water Waves Problem Mathematical Analysis and Asymptotics Mathematical Surveys and Monographs Volume 188 The Water Waves Problem Mathematical Analysis and Asymptotics David Lannes American Mathematical Society Providence, Rhode Island EDITORIAL COMMITTEE Ralph L. Cohen, Chair Benjamin Sudakov MichaelA.Singer MichaelI.Weinstein 2010 Mathematics Subject Classification. Primary 76B15, 35Q53, 35Q55, 35J05, 35J25. For additional information and updates on this book, visit www.ams.org/bookpages/surv-188 Library of Congress Cataloging-in-Publication Data Lannes, David, 1973– The water waves problem : mathematical analysis and asymptotics / David Lannes. pages cm. – (Mathematical surveys and monographs ; volume 188) Includes bibliographical references and index. ISBN 978-0-8218-9470-5 (alk. paper) 1.Water waves–Mathematical models. 2. Hydrodynamics–Mathematical models. I. Title. TC172.L36 2013 551.46301515–dc23 2012046540 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Requests for such permission should be addressed to the Acquisitions Department, American Mathematical Society, 201 Charles Street, Providence, Rhode Island 02904-2294 USA. Requests can also be made by e-mail to [email protected].
    [Show full text]
  • Final Report and Determination
    MARINE STEWARDSHIP COUNCIL FISHERY ASSESSMENT Final Report and Determination For The Association des Pêcheurs Propriétaires des Îles-de-la-Madeleine (APPIM) Îles-de-la-Madeleine lobster (Homarus americanus) Trap Fishery Assessors: Clare Murray, R.J. (Bob) Allain, Jean-Claude Brêthes, Géraldine Criquet, Dave Garforth Report Code: MSC 010 Date: 20th June 2013 Global Trust Certification Ltd. Head Office, 3rd Floor, Block 3, Quayside Business Park, Mill Street, Dundalk, Co. Louth. T: +353 42 9320912 F: +353 42 9386864 web: www.GTCert.com Global Trust Certification Ltd, 3rd Floor, Block 3, Quayside Business Park, Mill Street, Dundalk, Co. Louth, Ireland T: +353 42 932 0912 F: +353 42 938 6864E: [email protected]: w w w .GTcert.com Table of contents Glossary ....................................................................................................................................... 4 1.0 MSC FISHERY ASSESSMENT REPORT ..................................................................................... 5 1.1 Executive Summary ...................................................................................................... 6 1.2 Authorship and Peer Reviewers ............................................................................... 9 2.0 Description of the Fishery .................................................................................................. 11 2.1 Unit(s) of Certification and scope of certification sought ......................................... 11 2.1.1 Scope of Assessment in Relation to Enhanced Fisheries
    [Show full text]
  • Toe Structures Management Manual
    Toe structures management manual Project: SC070056/R The Environment Agency is the leading public body protecting and improving the environment in England and Wales. It’s our job to make sure that air, land and water are looked after by everyone in today’s society, so that tomorrow’s generations inherit a cleaner, healthier world. Our work includes tackling flooding and pollution incidents, reducing industry’s impacts on the environment, cleaning up rivers, coastal waters and contaminated land, and improving wildlife habitats. This report is the result of research commissioned and funded by the Environment Agency’s Evidence Directorate. Published by: Author(s): Environment Agency, Horison House, Deanery Road, Andy Bradbury Bristol, BS1 9AH Jonathan Rogers www.environment-agency.gov.uk Dick Thomas ISBN: 978-1-84911-290-1 Dissemination Status: Publicly available © Environment Agency – December 2012 Keywords: All rights reserved. This document may be reproduced Coastal structures, structure toe, asset management, with prior permission of the Environment Agency. condition assessment, beach, scour The views and statements expressed in this report are Research Contractor: those of the author alone. The views or statements Halcrow Group Ltd expressed in this publication do not necessarily Ash House, Falcon Road, Sowton, Exeter, Devon represent the views of the Environment Agency and the EX2 7LB Environment Agency cannot accept any responsibility for Tel: 01392 444252 such views or statements. Environment Agency’s Project Manager: Further copies of this report are available from our Dave Hart, Manley House, Exeter publications catalogue: http://publications.environment- agency.gov.uk or our National Customer Contact Collaborator(s): Centre: T: 08708 506506 None E: [email protected].
    [Show full text]