Lecture 3: Algebra and Languages 1. Overview 2. Syntactic Congruences
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Automata, Semigroups and Duality
Automata, semigroups and duality Mai Gehrke1 Serge Grigorieff2 Jean-Eric´ Pin2 1Radboud Universiteit 2LIAFA, CNRS and University Paris Diderot TANCL’07, August 2007, Oxford LIAFA, CNRS and University Paris Diderot Outline (1) Four ways of defining languages (2) The profinite world (3) Duality (4) Back to the future LIAFA, CNRS and University Paris Diderot Part I Four ways of defining languages LIAFA, CNRS and University Paris Diderot Words and languages Words over the alphabet A = {a, b, c}: a, babb, cac, the empty word 1, etc. The set of all words A∗ is the free monoid on A. A language is a set of words. Recognizable (or regular) languages can be defined in various ways: ⊲ by (extended) regular expressions ⊲ by finite automata ⊲ in terms of logic ⊲ by finite monoids LIAFA, CNRS and University Paris Diderot Basic operations on languages • Boolean operations: union, intersection, complement. • Product: L1L2 = {u1u2 | u1 ∈ L1,u2 ∈ L2} Example: {ab, a}{a, ba} = {aa, aba, abba}. • Star: L∗ is the submonoid generated by L ∗ L = {u1u2 · · · un | n > 0 and u1,...,un ∈ L} {a, ba}∗ = {1, a, aa, ba, aaa, aba, . .}. LIAFA, CNRS and University Paris Diderot Various types of expressions • Regular expressions: union, product, star: (ab)∗ ∪ (ab)∗a • Extended regular expressions (union, intersection, complement, product and star): A∗ \ (bA∗ ∪ A∗aaA∗ ∪ A∗bbA∗) • Star-free expressions (union, intersection, complement, product but no star): ∅c \ (b∅c ∪∅caa∅c ∪∅cbb∅c) LIAFA, CNRS and University Paris Diderot Finite automata a 1 2 The set of states is {1, 2, 3}. b The initial state is 1. b a 3 The final states are 1 and 2. -

Midterm Study Sheet for CS3719 Regular Languages and Finite
Midterm study sheet for CS3719 Regular languages and finite automata: • An alphabet is a finite set of symbols. Set of all finite strings over an alphabet Σ is denoted Σ∗.A language is a subset of Σ∗. Empty string is called (epsilon). • Regular expressions are built recursively starting from ∅, and symbols from Σ and closing under ∗ Union (R1 ∪ R2), Concatenation (R1 ◦ R2) and Kleene Star (R denoting 0 or more repetitions of R) operations. These three operations are called regular operations. • A Deterministic Finite Automaton (DFA) D is a 5-tuple (Q, Σ, δ, q0,F ), where Q is a finite set of states, Σ is the alphabet, δ : Q × Σ → Q is the transition function, q0 is the start state, and F is the set of accept states. A DFA accepts a string if there exists a sequence of states starting with r0 = q0 and ending with rn ∈ F such that ∀i, 0 ≤ i < n, δ(ri, wi) = ri+1. The language of a DFA, denoted L(D) is the set of all and only strings that D accepts. • Deterministic finite automata are used in string matching algorithms such as Knuth-Morris-Pratt algorithm. • A language is called regular if it is recognized by some DFA. • ‘Theorem: The class of regular languages is closed under union, concatenation and Kleene star operations. • A non-deterministic finite automaton (NFA) is a 5-tuple (Q, Σ, δ, q0,F ), where Q, Σ, q0 and F are as in the case of DFA, but the transition function δ is δ : Q × (Σ ∪ {}) → P(Q). -

Chapter 6 Formal Language Theory
Chapter 6 Formal Language Theory In this chapter, we introduce formal language theory, the computational theories of languages and grammars. The models are actually inspired by formal logic, enriched with insights from the theory of computation. We begin with the definition of a language and then proceed to a rough characterization of the basic Chomsky hierarchy. We then turn to a more de- tailed consideration of the types of languages in the hierarchy and automata theory. 6.1 Languages What is a language? Formally, a language L is defined as as set (possibly infinite) of strings over some finite alphabet. Definition 7 (Language) A language L is a possibly infinite set of strings over a finite alphabet Σ. We define Σ∗ as the set of all possible strings over some alphabet Σ. Thus L ⊆ Σ∗. The set of all possible languages over some alphabet Σ is the set of ∗ all possible subsets of Σ∗, i.e. 2Σ or ℘(Σ∗). This may seem rather simple, but is actually perfectly adequate for our purposes. 6.2 Grammars A grammar is a way to characterize a language L, a way to list out which strings of Σ∗ are in L and which are not. If L is finite, we could simply list 94 CHAPTER 6. FORMAL LANGUAGE THEORY 95 the strings, but languages by definition need not be finite. In fact, all of the languages we are interested in are infinite. This is, as we showed in chapter 2, also true of human language. Relating the material of this chapter to that of the preceding two, we can view a grammar as a logical system by which we can prove things. -
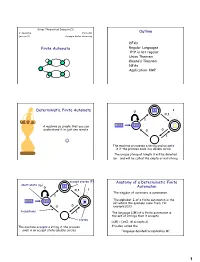
Deterministic Finite Automata 0 0,1 1
Great Theoretical Ideas in CS V. Adamchik CS 15-251 Outline Lecture 21 Carnegie Mellon University DFAs Finite Automata Regular Languages 0n1n is not regular Union Theorem Kleene’s Theorem NFAs Application: KMP 11 1 Deterministic Finite Automata 0 0,1 1 A machine so simple that you can 0111 111 1 ϵ understand it in just one minute 0 0 1 The machine processes a string and accepts it if the process ends in a double circle The unique string of length 0 will be denoted by ε and will be called the empty or null string accept states (F) Anatomy of a Deterministic Finite start state (q0) 11 0 Automaton 0,1 1 The singular of automata is automaton. 1 The alphabet Σ of a finite automaton is the 0111 111 1 ϵ set where the symbols come from, for 0 0 example {0,1} transitions 1 The language L(M) of a finite automaton is the set of strings that it accepts states L(M) = {x∈Σ: M accepts x} The machine accepts a string if the process It’s also called the ends in an accept state (double circle) “language decided/accepted by M”. 1 The Language L(M) of Machine M The Language L(M) of Machine M 0 0 0 0,1 1 q 0 q1 q0 1 1 What language does this DFA decide/accept? L(M) = All strings of 0s and 1s The language of a finite automaton is the set of strings that it accepts L(M) = { w | w has an even number of 1s} M = (Q, Σ, , q0, F) Q = {q0, q1, q2, q3} Formal definition of DFAs where Σ = {0,1} A finite automaton is a 5-tuple M = (Q, Σ, , q0, F) q0 Q is start state Q is the finite set of states F = {q1, q2} Q accept states : Q Σ → Q transition function Σ is the alphabet : Q Σ → Q is the transition function q 1 0 1 0 1 0,1 q0 Q is the start state q0 q0 q1 1 q q1 q2 q2 F Q is the set of accept states 0 M q2 0 0 q2 q3 q2 q q q 1 3 0 2 L(M) = the language of machine M q3 = set of all strings machine M accepts EXAMPLE Determine the language An automaton that accepts all recognized by and only those strings that contain 001 1 0,1 0,1 0 1 0 0 0 1 {0} {00} {001} 1 L(M)={1,11,111, …} 2 Membership problem Determine the language decided by Determine whether some word belongs to the language. -
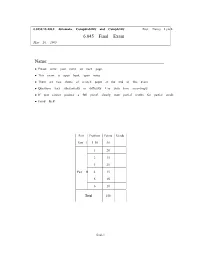
6.045 Final Exam Name
6.045J/18.400J: Automata, Computability and Complexity Prof. Nancy Lynch 6.045 Final Exam May 20, 2005 Name: • Please write your name on each page. • This exam is open book, open notes. • There are two sheets of scratch paper at the end of this exam. • Questions vary substantially in difficulty. Use your time accordingly. • If you cannot produce a full proof, clearly state partial results for partial credit. • Good luck! Part Problem Points Grade Part I 1–10 50 1 20 2 15 3 25 Part II 4 15 5 15 6 10 Total 150 final-1 Name: Part I Multiple Choice Questions. (50 points, 5 points for each question) For each question, any number of the listed answersClearly may place be correct. an “X” in the box next to each of the answers that you are selecting. Problem 1: Which of the following are true statements about regular and nonregular languages? (All lan guages are over the alphabet{0, 1}) IfL1 ⊆ L2 andL2 is regular, thenL1 must be regular. IfL1 andL2 are nonregular, thenL1 ∪ L2 must be nonregular. IfL1 is nonregular, then the complementL 1 must of also be nonregular. IfL1 is regular,L2 is nonregular, andL1 ∩ L2 is nonregular, thenL1 ∪ L2 must be nonregular. IfL1 is regular,L2 is nonregular, andL1 ∩ L2 is regular, thenL1 ∪ L2 must be nonregular. Problem 2: Which of the following are guaranteed to be regular languages ? ∗ L2 = {ww : w ∈{0, 1}}. L2 = {ww : w ∈ L1}, whereL1 is a regular language. L2 = {w : ww ∈ L1}, whereL1 is a regular language. L2 = {w : for somex,| w| = |x| andwx ∈ L1}, whereL1 is a regular language. -

(A) for Any Regular Expression R, the Set L(R) of Strings
Kleene’s Theorem Definition. Alanguageisregular iff it is equal to L(M), the set of strings accepted by some deterministic finite automaton M. Theorem. (a) For any regular expression r,thesetL(r) of strings matching r is a regular language. (b) Conversely, every regular language is the form L(r) for some regular expression r. L6 79 Example of a regular language Recall the example DFA we used earlier: b a a a a M ! q0 q1 q2 q3 b b b In this case it’s not hard to see that L(M)=L(r) for r =(a|b)∗ aaa(a|b)∗ L6 80 Example M ! a 1 b 0 b a a 2 L(M)=L(r) for which regular expression r? Guess: r = a∗|a∗b(ab)∗ aaa∗ L6 81 Example M ! a 1 b 0 b a a 2 L(M)=L(r) for which regular expression r? Guess: r = a∗|a∗b(ab)∗ aaa∗ since baabaa ∈ L(M) WRONG! but baabaa ̸∈ L(a∗|a∗b(ab)∗ aaa∗ ) We need an algorithm for constructing a suitable r for each M (plus a proof that it is correct). L6 81 Lemma. Given an NFA M =(Q, Σ, δ, s, F),foreach subset S ⊆ Q and each pair of states q, q′ ∈ Q,thereisa S regular expression rq,q′ satisfying S Σ∗ u ∗ ′ L(rq,q′ )={u ∈ | q −→ q in M with all inter- mediate states of the sequence of transitions in S}. Hence if the subset F of accepting states has k distinct elements, q1,...,qk say, then L(M)=L(r) with r ! r1|···|rk where Q ri = rs,qi (i = 1, . -

A Quantum Query Complexity Trichotomy for Regular Languages
A Quantum Query Complexity Trichotomy for Regular Languages Scott Aaronson∗ Daniel Grier† Luke Schaeffer UT Austin MIT MIT [email protected] [email protected] [email protected] Abstract We present a trichotomy theorem for the quantum query complexity of regular languages. Every regular language has quantum query complexity Θ(1), Θ˜ (√n), or Θ(n). The extreme uniformity of regular languages prevents them from taking any other asymptotic complexity. This is in contrast to even the context-free languages, which we show can have query complex- ity Θ(nc) for all computable c [1/2,1]. Our result implies an equivalent trichotomy for the approximate degree of regular∈ languages, and a dichotomy—either Θ(1) or Θ(n)—for sensi- tivity, block sensitivity, certificate complexity, deterministic query complexity, and randomized query complexity. The heart of the classification theorem is an explicit quantum algorithm which decides membership in any star-free language in O˜ (√n) time. This well-studied family of the regu- lar languages admits many interesting characterizations, for instance, as those languages ex- pressible as sentences in first-order logic over the natural numbers with the less-than relation. Therefore, not only do the star-free languages capture functions such as OR, they can also ex- press functions such as “there exist a pair of 2’s such that everything between them is a 0.” Thus, we view the algorithm for star-free languages as a nontrivial generalization of Grover’s algorithm which extends the quantum quadratic speedup to a much wider range of string- processing algorithms than was previously known. -

Formal Languages We’Ll Use the English Language As a Running Example
Formal Languages We’ll use the English language as a running example. Definitions. Examples. A string is a finite set of symbols, where • each symbol belongs to an alphabet de- noted by Σ. The set of all strings that can be constructed • from an alphabet Σ is Σ ∗. If x, y are two strings of lengths x and y , • then: | | | | – xy or x y is the concatenation of x and y, so the◦ length, xy = x + y | | | | | | – (x)R is the reversal of x – the kth-power of x is k ! if k =0 x = k 1 x − x, if k>0 ! ◦ – equal, substring, prefix, suffix are de- fined in the expected ways. – Note that the language is not the same language as !. ∅ 73 Operations on Languages Suppose that LE is the English language and that LF is the French language over an alphabet Σ. Complementation: L = Σ L • ∗ − LE is the set of all words that do NOT belong in the english dictionary . Union: L1 L2 = x : x L1 or x L2 • ∪ { ∈ ∈ } L L is the set of all english and french words. E ∪ F Intersection: L1 L2 = x : x L1 and x L2 • ∩ { ∈ ∈ } LE LF is the set of all words that belong to both english and∩ french...eg., journal Concatenation: L1 L2 is the set of all strings xy such • ◦ that x L1 and y L2 ∈ ∈ Q: What is an example of a string in L L ? E ◦ F goodnuit Q: What if L or L is ? What is L L ? E F ∅ E ◦ F ∅ 74 Kleene star: L∗. -

A Categorical Approach to Syntactic Monoids 11
Logical Methods in Computer Science Vol. 14(2:9)2018, pp. 1–34 Submitted Jan. 15, 2016 https://lmcs.episciences.org/ Published May 15, 2018 A CATEGORICAL APPROACH TO SYNTACTIC MONOIDS JIRˇ´I ADAMEK´ a, STEFAN MILIUS b, AND HENNING URBAT c a Institut f¨urTheoretische Informatik, Technische Universit¨atBraunschweig, Germany e-mail address: [email protected] b;c Lehrstuhl f¨urTheoretische Informatik, Friedrich-Alexander-Universit¨atErlangen-N¨urnberg, Ger- many e-mail address: [email protected], [email protected] Abstract. The syntactic monoid of a language is generalized to the level of a symmetric monoidal closed category D. This allows for a uniform treatment of several notions of syntactic algebras known in the literature, including the syntactic monoids of Rabin and Scott (D “ sets), the syntactic ordered monoids of Pin (D “ posets), the syntactic semirings of Pol´ak(D “ semilattices), and the syntactic associative algebras of Reutenauer (D = vector spaces). Assuming that D is a commutative variety of algebras or ordered algebras, we prove that the syntactic D-monoid of a language L can be constructed as a quotient of a free D-monoid modulo the syntactic congruence of L, and that it is isomorphic to the transition D-monoid of the minimal automaton for L in D. Furthermore, in the case where the variety D is locally finite, we characterize the regular languages as precisely the languages with finite syntactic D-monoids. 1. Introduction One of the successes of the theory of coalgebras is that ideas from automata theory can be developed at a level of abstraction where they apply uniformly to many different types of systems. -

Syntactic Semigroups
Syntactic semigroups Jean-Eric Pin LITP/IBP, CNRS, Universit´e Paris VI, 4 Place Jussieu, 75252 Paris Cedex 05, FRANCE 1 Introduction This chapter gives an overview on what is often called the algebraic theory of finite automata. It deals with languages, automata and semigroups, and has connections with model theory in logic, boolean circuits, symbolic dynamics and topology. Kleene's theorem [70] is usually considered as the foundation of this theory. It shows that the class of recognizable languages (i.e. recognized by finite automata), coincides with the class of rational languages, which are given by rational expressions. The definition of the syntactic mono- id, a monoid canonically attached to each language, was first given in an early paper of Rabin and Scott [128], where the notion is credited to Myhill. It was shown in particular that a language is recognizable if and only if its syntactic monoid is finite. However, the first classification results were rather related to automata [89]. A break-through was realized by Schutzen-¨ berger in the mid sixties [144]. Schutzenb¨ erger made a non trivial use of the syntactic monoid to characterize an important subclass of the rational languages, the star-free languages. Schutzenb¨ erger's theorem states that a language is star-free if and only if its syntactic monoid is finite and aperiodic. This theorem had a considerable influence on the theory. Two other im- portant \syntactic" characterizations were obtained in the early seventies: Simon [152] proved that a language is piecewise testable if and only if its syntactic monoid is finite and J -trivial and Brzozowski-Simon [41] and in- dependently, McNaughton [86] characterized the locally testable languages. -

Using Jflap in Academics to Understand Automata Theory in a Better Way
International Journal of Advances in Electronics and Computer Science, ISSN: 2393-2835 Volume-5, Issue-5, May.-2018 http://iraj.in USING JFLAP IN ACADEMICS TO UNDERSTAND AUTOMATA THEORY IN A BETTER WAY KAVITA TEWANI Assistant Professor, Institute of Technology, Nirma University E-mail: [email protected] Abstract - As it is been observed that the things get much easier once we visualize it and hence this paper is just a step towards it. Usually many subjects in computer engineering curriculum like algorithms, data structures, and theory of computation are taught theoretically however it lacks the visualization that may help students to understand the concepts in a better way. The paper shows some of the practices on tool called JFLAP (Java Formal Languages and Automata Package) and the statistics on how it affected the students to learn the concepts easily. The diagrammatic representation is used to help the theory mentioned. Keywords - Automata, JFLAP, Grammar, Chomsky Heirarchy , Turing Machine, DFA, NFA I. INTRODUCTION visualization and interaction in the course is enhanced through the popular software tools[6,7]. The proper The theory of computation is a basic course in use of JFLAP and instructions are provided in the computer engineering discipline. It is the subject manual “JFLAP activities for Formal Languages and which is been taught theoretically and hands-on Automata” by Peter Linz and Susan Rodger. It problems are given to the students to enhance the includes the theoretical approach and their understanding but it lacks the programming implementation in JFLAP. [10] assignment. However the subject is the base for creation of compilers and therefore should be given III. -

Typed Monoids – an Eilenberg-Like Theorem for Non Regular Languages
Electronic Colloquium on Computational Complexity, Report No. 35 (2011) Typed Monoids – An Eilenberg-like Theorem for non regular Languages Christoph Behle Andreas Krebs Stephanie Reifferscheid∗ Wilhelm-Schickard-Institut, Universität Tübingen, fbehlec,krebs,reiff[email protected] Abstract Based on different concepts to obtain a finer notion of language recognition via finite monoids we develop an algebraic structure called typed monoid. This leads to an algebraic description of regular and non regular languages. We obtain for each language a unique minimal recognizing typed monoid, the typed syntactic monoid. We prove an Eilenberg-like theorem for varieties of typed monoids as well as a similar correspondence for classes of languages with weaker closure properties. 1 Introduction We present an algebraic viewpoint on the study of formal languages and introduce a new algebraic structure to describe formal languages. We extend the known approach to use language recognition via monoids and morphisms by equipping the monoids with additional information to obtain a finer notion of recognition. In the concept of language recognition by monoids, a language L ⊆ Σ∗ is recognized by a monoid M if there exists a morphism h : Σ∗ ! M and a subset A of M such that L = h−1(A). The syntactic monoid, which is the smallest monoid recognizing L, has emerged as an important tool to study classes of regular languages. Besides problems applying this tool to non regular languages, even for regular languages this instrument lacks precision. One problem is, that not only the syntactic monoid but also the syntactic mor- phism, i.e. the morphism recognizing L via the syntactic monoid, plays an important role: Consider the two languages Lparity, Leven over the alphabet Σ = fa; bg where the first one consists of all words with an even number of a’s while the latter consists of all words of even length.