DOCSLIB.ORG

Classical Mechanics - Wikipedia, the Free Encyclopedia Page 1 of 13

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Classical Mechanics - Wikipedia, the Free Encyclopedia Page 1 of 13 Classical mechanics - Wikipedia, the free encyclopedia Page 1 of 13 Classical mechanics From Wikipedia, the free encyclopedia (Redirected from Newtonian mechanics) In physics, classical mechanics is one of the two major Classical mechanics sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the Newton's Second Law action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of History of classical mechanics · the oldest and largest subjects in science, engineering and Timeline of classical mechanics technology. Branches Classical mechanics describes the motion of macroscopic Statics · Dynamics / Kinetics · Kinematics · objects, from projectiles to parts of machinery, as well as Applied mechanics · Celestial mechanics · astronomical objects, such as spacecraft, planets, stars, and Continuum mechanics · galaxies. Besides this, many specializations within the Statistical mechanics subject deal with gases, liquids, solids, and other specific sub-topics. Classical mechanics provides extremely Formulations accurate results as long as the domain of study is restricted Newtonian mechanics (Vectorial to large objects and the speeds involved do not approach mechanics) the speed of light. When the objects being dealt with become sufficiently small, it becomes necessary to Analytical mechanics: introduce the other major sub-field of mechanics, quantum Lagrangian mechanics mechanics, which reconciles the macroscopic laws of Hamiltonian mechanics physics with the atomic nature of matter and handles the Fundamental concepts wave-particle duality of atoms and molecules. In the case of high velocity objects approaching the speed of light, Space · Time · Velocity · Speed · Mass · classical mechanics is enhanced by special relativity. Acceleration · Gravity · Force · Impulse · General relativity unifies special relativity with Newton's Torque / Moment / Couple · Momentum · law of universal gravitation, allowing physicists to handle Angular momentum · Inertia · gravitation at a deeper level. Moment of inertia · Reference frame · The term classical mechanics was coined in the early 20th Energy · Kinetic energy · Potential energy · century to describe the system of physics begun by Isaac Mechanical work · Virtual work · Newton and many contemporary 17th century natural D'Alembert's principle philosophers, building upon the earlier astronomical theories of Johannes Kepler, which in turn were based on Core topics the precise observations of Tycho Brahe and the studies of Rigid body · Rigid body dynamics · terrestrial projectile motion of Galileo. Because these Euler's equations (rigid body dynamics) · aspects of physics were developed long before the emergence of quantum physics and relativity, some sources Motion · Newton's laws of motion · exclude Einstein's theory of relativity from this category. Newton's law of universal gravitation · However, a number of modern sources do include Equations of motion · relativistic mechanics, which in their view represents Inertial frame of reference · classical mechanics in its most developed and most Non-inertial reference frame · [note 1] accurate form. Rotating reference frame · Fictitious force · The initial stage in the development of classical mechanics Linear motion · is often referred to as Newtonian mechanics, and is Mechanics of planar particle motion · associated with the physical concepts employed by and the Displacement (vector) · Relative velocity · http://en.wikipedia.org/wiki/Newtonian_mechanics 5/23/2011 Classical mechanics - Wikipedia, the free encyclopedia Page 2 of 13 mathematical methods invented by Newton himself, in parallel with Leibniz, and others. This is further described Friction · Simple harmonic motion · in the following sections. Later, more abstract and general Harmonic oscillator · Vibration · Damping · methods were developed, leading to reformulations of Damping ratio · Rotational motion · classical mechanics known as Lagrangian mechanics and Circular motion · Uniform circular motion · Hamiltonian mechanics. These advances were largely made in the 18th and 19th centuries, and they extend Non-uniform circular motion · substantially beyond Newton's work, particularly through Centripetal force · Centrifugal force · their use of analytical mechanics. Ultimately, the Centrifugal force (rotating reference frame) · mathematics developed for these were central to the Reactive centrifugal force · Coriolis force · creation of quantum mechanics. Pendulum · Rotational speed · Angular acceleration · Angular velocity · Contents Angular frequency · Angular displacement Scientists 1 Description of the theory 1.1 Position and its derivatives Galileo Galilei · Isaac Newton · 1.1.1 Velocity and speed Jeremiah Horrocks · Leonhard Euler · 1.1.2 Acceleration Jean le Rond d'Alembert · Alexis Clairaut · 1.1.3 Frames of reference Joseph Louis Lagrange · 1.2 Forces; Newton's second law Pierre-Simon Laplace · 1.3 Work and energy William Rowan Hamilton · 1.4 Beyond Newton's Laws Siméon-Denis Poisson 2 History 3 Limits of validity 3.1 The Newtonian approximation to special relativity 3.2 The classical approximation to quantum mechanics 4 Branches 5 See also 6 Notes 7 References 8 Further reading 9 External links Description of the theory The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it. Each of these parameters is discussed in turn. In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as http://en.wikipedia.org/wiki/Newtonian_mechanics 5/23/2011 Classical mechanics - Wikipedia, the free encyclopedia Page 3 of 13 composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle. The analysis of projectile motion is a part of classical mechanics. Position and its derivatives Main article: Kinematics The position of a point particle is defined with respect The SI derived "mechanical" to an arbitrary fixed reference point, O, in space, (that is, not electromagnetic or thermal) usually accompanied by a coordinate system, with the units with kg, m and s reference point located at the origin of the coordinate Position m system. It is defined as the vector r from O to the particle. In general, the point particle need not be Angular position/Angle unitless (radian) stationary relative to O, so r is a function of t, the time velocity m s −1 elapsed since an arbitrary initial time. In pre-Einstein −1 relativity (known as Galilean relativity), time is Angular velocity s considered an absolute, i.e., the time interval between acceleration m s −2 any given pair of events is the same for all observers. In addition to relying on absolute time, classical Angular acceleration s−2 mechanics assumes Euclidean geometry for the jerk m s −3 structure of space. [1] "Angular jerk" s−3 Velocity and speed specific energy m2 s −2 Main articles: Velocity and speed absorbed dose rate m2 s −3 2 The velocity , or the rate of change of position with moment of inertia kg m time, is defined as the derivative of the position with momentum kg m s −1 respect to time or 2 −1 angular momentum kg m s −2 . force kg m s torque kg m 2 s −2 In classical mechanics, velocities are directly additive energy kg m 2 s −2 and subtractive. For example, if one car traveling East http://en.wikipedia.org/wiki/Newtonian_mechanics 5/23/2011 Classical mechanics - Wikipedia, the free encyclopedia Page 4 of 13 at 60 km/h passes another car traveling East at 50 km/h, power kg m 2 s −3 then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, pressure and energy density kg m −1 s −2 from the perspective of the faster car, the slower car is −2 moving 10 km/h to the West. Velocities are directly surface tension kg s additive as vector quantities ; they must be dealt with Spring constant kg s −2 using vector analysis. irradiance and energy flux kg s −3 Mathematically, if the velocity of the first object in the kinematic viscosity 2 −1 previous discussion is denoted by the vector u = ud and m s the velocity of the second object by the vector v = ve, dynamic viscosity kg m −1 s −1 where u is the speed of the first object, v is the speed of −3 the second object, and d and e are unit vectors in the Density(mass density) kg m directions of motion of each particle respectively, then Density(weight density) kg m −2 s −2 the velocity of the first object as seen by the second object is Number density m−3 Action 2 −1 kg m s Similarly, When both objects are moving in the same direction, this equation can be simplified to Or, by ignoring direction, the difference can be given in terms of speed only: Acceleration Main article: Acceleration The acceleration , or rate of change of velocity, is the derivative of the velocity with respect
Load more

Recommended publications
  • WUN2K for LECTURE 19 These Are Notes Summarizing the Main Concepts You Need to Understand and Be Able to Apply
    Duke University Department of Physics Physics 361 Spring Term 2020 WUN2K FOR LECTURE 19 These are notes summarizing the main concepts you need to understand and be able to apply. • Newton's Laws are valid only in inertial reference frames. However, it is often possible to treat motion in noninertial reference frames, i.e., accelerating ones. • For a frame with rectilinear acceleration A~ with respect to an inertial one, we can write the equation of motion as m~r¨ = F~ − mA~, where F~ is the force in the inertial frame, and −mA~ is the inertial force. The inertial force is a “fictitious” force: it's a quantity that one adds to the equation of motion to make it look as if Newton's second law is valid in a noninertial reference frame. • For a rotating frame: Euler's theorem says that the most general mo- tion of any body with respect to an origin is rotation about some axis through the origin. We define an axis directionu ^, a rate of rotation dθ about that axis ! = dt , and an instantaneous angular velocity ~! = !u^, with direction given by the right hand rule (fingers curl in the direction of rotation, thumb in the direction of ~!.) We'll generally use ~! to refer to the angular velocity of a body, and Ω~ to refer to the angular velocity of a noninertial, rotating reference frame. • We have for the velocity of a point at ~r on the rotating body, ~v = ~! ×~r. ~ dQ~ dQ~ ~ • Generally, for vectors Q, one can write dt = dt + ~! × Q, for S0 S0 S an inertial reference frame and S a rotating reference frame.
    [Show full text]
  • Rotating Reference Frame Control of Switched Reluctance
    ROTATING REFERENCE FRAME CONTROL OF SWITCHED RELUCTANCE MACHINES A Thesis Presented to The Graduate Faculty of The University of Akron In Partial Fulfillment of the Requirements for the Degree Master of Science Tausif Husain August, 2013 ROTATING REFERENCE FRAME CONTROL OF SWITCHED RELUCTANCE MACHINES Tausif Husain Thesis Approved: Accepted: _____________________________ _____________________________ Advisor Department Chair Dr. Yilmaz Sozer Dr. J. Alexis De Abreu Garcia _____________________________ _____________________________ Committee Member Dean of the College Dr. Malik E. Elbuluk Dr. George K. Haritos _____________________________ _____________________________ Committee Member Dean of the Graduate School Dr. Tom T. Hartley Dr. George R. Newkome _____________________________ Date ii ABSTRACT A method to control switched reluctance motors (SRM) in the dq rotating frame is proposed in this thesis. The torque per phase is represented as the product of a sinusoidal inductance related term and a sinusoidal current term in the SRM controller. The SRM controller works with variables similar to those of a synchronous machine (SM) controller in dq reference frame, which allows the torque to be shared smoothly among different phases. The proposed controller provides efficient operation over the entire speed range and eliminates the need for computationally intensive sequencing algorithms. The controller achieves low torque ripple at low speeds and can apply phase advancing using a mechanism similar to the flux weakening of SM to operate at high speeds. A method of adaptive flux weakening for ensured operation over a wide speed range is also proposed. This method is developed for use with dq control of SRM but can also work in other controllers where phase advancing is required.
    [Show full text]
  • Principle of Relativity and Inertial Dragging
    ThePrincipleofRelativityandInertialDragging By ØyvindG.Grøn OsloUniversityCollege,Departmentofengineering,St.OlavsPl.4,0130Oslo, Norway Email: [email protected] Mach’s principle and the principle of relativity have been discussed by H. I. HartmanandC.Nissim-Sabatinthisjournal.Severalphenomenaweresaidtoviolate the principle of relativity as applied to rotating motion. These claims have recently been contested. However, in neither of these articles have the general relativistic phenomenonofinertialdraggingbeeninvoked,andnocalculationhavebeenoffered byeithersidetosubstantiatetheirclaims.HereIdiscussthepossiblevalidityofthe principleofrelativityforrotatingmotionwithinthecontextofthegeneraltheoryof relativity, and point out the significance of inertial dragging in this connection. Although my main points are of a qualitative nature, I also provide the necessary calculationstodemonstratehowthesepointscomeoutasconsequencesofthegeneral theoryofrelativity. 1 1.Introduction H. I. Hartman and C. Nissim-Sabat 1 have argued that “one cannot ascribe all pertinentobservationssolelytorelativemotionbetweenasystemandtheuniverse”. They consider an UR-scenario in which a bucket with water is atrest in a rotating universe,andaBR-scenariowherethebucketrotatesinanon-rotatinguniverseand givefiveexamplestoshowthatthesesituationsarenotphysicallyequivalent,i.e.that theprincipleofrelativityisnotvalidforrotationalmotion. When Einstein 2 presented the general theory of relativity he emphasized the importanceofthegeneralprincipleofrelativity.Inasectiontitled“TheNeedforan
    [Show full text]
  • Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
    Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time.
    [Show full text]
  • Static Limit and Penrose Effect in Rotating Reference Frames
    1 Static limit and Penrose effect in rotating reference frames A. A. Grib∗ and Yu. V. Pavlov† We show that effects similar to those for a rotating black hole arise for an observer using a uniformly rotating reference frame in a flat space-time: a surface appears such that no body can be stationary beyond this surface, while the particle energy can be either zero or negative. Beyond this surface, which is similar to the static limit for a rotating black hole, an effect similar to the Penrose effect is possible. We consider the example where one of the fragments of a particle that has decayed into two particles beyond the static limit flies into the rotating reference frame inside the static limit and has an energy greater than the original particle energy. We obtain constraints on the relative velocity of the decay products during the Penrose process in the rotating reference frame. We consider the problem of defining energy in a noninertial reference frame. For a uniformly rotating reference frame, we consider the states of particles with minimum energy and show the relation of this quantity to the radiation frequency shift of the rotating body due to the transverse Doppler effect. Keywords: rotating reference frame, negative-energy particle, Penrose effect 1. Introduction The study of relativistic effects related to rotation began immediately after the theory of relativity appeared [1], and such effects are still actively discussed in the literature [2]. The importance of studying such effects is obvious in relation to the Earth’s rotation. In [3], we compared the properties of particles in rotating reference frames in a flat space with the properties of particles in the metric of a rotating black hole.
    [Show full text]
  • Jeremiah Horrocks's Lancashire
    Transits of Venus: New Views of the Solar System and Galaxy Proceedings IAU Colloquium No. 196, 2004 c 2004 International Astronomical Union D.W. Kurtz, ed. doi:10.1017/S1743921305001237 Jeremiah Horrocks’s Lancashire John K. Walton Department of History, University of Central Lancashire, Preston PR1 2HE, UK (email: [email protected]) Abstract. This paper sets Jeremiah Horrocks and Much Hoole in the context of Lancashire society on the eve of the English Civil War. It focuses on the complexities of what it was to be a “Puritan” in an environment where religious labels and conflicts mattered a great deal; it examines the economic circumstances of county and locality at the time, pointing out the extent to which (despite widespread and deep poverty) the county’s merchants were looking outwards to London, northern Europe and beyond; and it emphasizes that even in the apparently remote and rustic location of Much Hoole it was possible for Horrocks to sustain a scientific correspondence and to keep in touch with, and make his contribution to, developments on a much wider stage. This contribution is intended to complement Allan Chapman’s plenary lecture by devel- oping the local and Lancashire dimension to Jeremiah Horrocks’s astronomical activities at Much Hoole, less than three years before the outbreak of the great Civil War in 1642, which culminated in the execution of Charles I in 1649 and ushered in Britain’s only pe- riod of republican government, which lasted until the Restoration in 1660 (see Chapman 1994, to which this paper runs
    [Show full text]
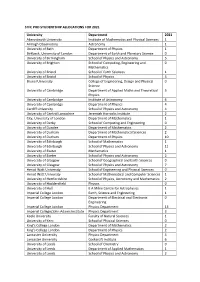
  • STFC Phd Studentship Allocation for 2021
    STFC PHD STUDENTSHIP ALLOCATIONS FOR 2021 University Department 2021 Aberystwyth University Institute of Mathematics and Physical Sciences 1 Armagh Observatory Astronomy 1 University of Bath Department of Physics 1 Birkbeck, University of London Department of Earth and Planetary Science 0 University of Birmingham School of Physics and Astronomy 5 University of Brighton School of Computing, Engineering and 0 Mathematics University of Bristol School of Earth Sciences 1 University of Bristol School of Physics 3 Brunel University College of Engineering, Design and Physical 0 Science University of Cambridge Department of Applied Maths and Theoretical 5 Physics University of Cambridge Institute of Astronomy 6 University of Cambridge Department of Physics 4 Cardiff University School of Physics and Astronomy 4 University of Central Lancashire Jeremiah Horrocks Institute 2 City, University of London Department of Mathematics 1 University of Derby School of Computing and Engineering 0 University of Dundee Department of Mathematics 2 University of Durham Department of Mathematical Sciences 2 University of Durham Department of Physics 10 University of Edinburgh School of Mathematics 1 University of Edinburgh School of Physics and Astronomy 11 University of Exeter Mathematics 1 University of Exeter School of Physics and Astronomy 2 University of Glasgow School of Geographical and Earth Sciences 0 University of Glasgow School of Physics and Astronomy 7 Heriot Watt University School of Engineering and Physical Sciences 0 Heriot Watt University School
    [Show full text]
  • Chapter 6 the Equations of Fluid Motion
    Chapter 6 The equations of fluid motion In order to proceed further with our discussion of the circulation of the at- mosphere, and later the ocean, we must develop some of the underlying theory governing the motion of a fluid on the spinning Earth. A differen- tially heated, stratified fluid on a rotating planet cannot move in arbitrary paths. Indeed, there are strong constraints on its motion imparted by the angular momentum of the spinning Earth. These constraints are profoundly important in shaping the pattern of atmosphere and ocean circulation and their ability to transport properties around the globe. The laws governing the evolution of both fluids are the same and so our theoretical discussion willnotbespecifictoeitheratmosphereorocean,butcanandwillbeapplied to both. Because the properties of rotating fluids are often counter-intuitive and sometimes difficult to grasp, alongside our theoretical development we will describe and carry out laboratory experiments with a tank of water on a rotating table (Fig.6.1). Many of the laboratory experiments we make use of are simplified versions of ‘classics’ that have become cornerstones of geo- physical fluid dynamics. They are listed in Appendix 13.4. Furthermore we have chosen relatively simple experiments that, in the main, do nor require sophisticated apparatus. We encourage you to ‘have a go’ or view the atten- dant movie loops that record the experiments carried out in preparation of our text. We now begin a more formal development of the equations that govern the evolution of a fluid. A brief summary of the associated mathematical concepts, definitions and notation we employ can be found in an Appendix 13.2.
    [Show full text]
  • Appendix A: Educational Resources in Astronomy
    Appendix A: Educational Resources in Astronomy A.I Planetariums, Museums, and Exhibits A.I.I Planetariums and Museums in the United Kingdom England - AAC Planetarium, Amateur Astronomy Centre, Bacup Road, Clough Bank, Tod­ morden, Lancs. OLl4 7HW. Tel: 0706816964. - British Museum, Great Russell Street, London WC1B 3DG; Tel: 071-323 8395 ext. 395. Astronomical clocks. - British Museum (Natural History), Cromwell Road, South Kensington, London SW7 5BD; Tel: 071-938 9123. Extensive meteorite collection. - Caird Planetarium, Old Royal Observatory, Greenwich, London SE 10. - William Day Planetarium, Plymouth Polytechnic, School of Maritime Studies, Ply- mouth PL4 8AA. Tel: 0752 264666. - Electrosonic Ltd., 815 Woolwich Road, London SE7 8LT. - Greenwich Planetarium, South Building, Greenwich Park, Greenwich, London SE 10. Tel: 081-858 1167. - William Herschel House and Museum, 19 New King Street, Bath, BA1 2Bl. Con­ tact: Dr. A.V. Sims, 30 Meadow Park, Bathford, Bath; Tel: 0225 859529. Open Mar-Oct daily 2-5 pm, Nov-Feb Sundays only, 2-5 pm. - lodrell Bank Planetarium and Visitor Center, Lower Withington, Nr. Macclesfield, Cheshire SK11 9DL; Tel: 0477 71339. - Kings Observatory, Kew, Old Deer Park, Richmond, Surrey TW9 2AZ. - University of Leicester, The Planetarium, Department of Astronomy, University Road, Leicester LEI 7RH; Tel: 0533 522522. - Liverpool Museum Planetarium, William Brown Street, Liverpool, Merseyside L3 8EN. Tel: 051-2070001 ext. 225. - London Planetarium, Marylebone Road, London NW1 5LR; Tel: 071-486 1121 (9:30--5:30), 071-486 1121 (recording). - City of London Polytechnic, The Planetarium, 100 Minories, Tower Hill, London EC3N BY. 071-283 1030. - London Schools Planetarium, John Archer School Building, Wandsworth Rd., Sutherland Grove, London SW18; Tel: 081-788 4253.
    [Show full text]
  • Classical Mechanics
    Stony Brook University Academic Commons Essential Graduate Physics Department of Physics and Astronomy 2013 Part CM: Classical Mechanics Konstantin Likharev SUNY Stony Brook, [email protected] Follow this and additional works at: https://commons.library.stonybrook.edu/egp Part of the Physics Commons Recommended Citation Likharev, Konstantin, "Part CM: Classical Mechanics" (2013). Essential Graduate Physics. 2. https://commons.library.stonybrook.edu/egp/2 This Book is brought to you for free and open access by the Department of Physics and Astronomy at Academic Commons. It has been accepted for inclusion in Essential Graduate Physics by an authorized administrator of Academic Commons. For more information, please contact [email protected], [email protected]. Konstantin K. Likharev Essential Graduate Physics Lecture Notes and Problems Beta version Open online access at http://commons.library.stonybrook.edu/egp/ and https://sites.google.com/site/likharevegp/ Part CM: Classical Mechanics Last corrections: September 10, 2021 A version of this material was published in 2017 under the title Classical Mechanics: Lecture notes IOPP, Essential Advanced Physics – Volume 1, ISBN 978-0-7503-1398-8, with model solutions of the exercise problems published in 2018 under the title Classical Mechanics: Problems with solutions IOPP, Essential Advanced Physics – Volume 2, ISBN 978-0-7503-1401-5 However, by now this online version of the lecture notes and the problem solutions available from the author, have been better corrected Note also: Konstantin K. Likharev (ed.) Essential Quotes for Scientists and Engineers Springer, 2021, ISBN 978-3-030-63331-8 (see https://essentialquotes.wordpress.com/) © K.
    [Show full text]
  • Kiss of the Goddess | the Economist
    5/9/2016 Kiss of the goddess | The Economist Transits of Venus Kiss of the goddess Venus will soon cross the face of the sun, and astronomers around the world will have a party May 27th 2004 | From the print edition FOR about six hours on Tuesday June 8th, the sun will be fainter than usual. There is no need to panic. It will fade by a mere 0.1%. Only a diligent observer with the correct viewing equipment will notice something odd: there will be a small, dark dot on the disc of the sun, like a solitary pea on a yellow dinner plate. The pea is Venus, passing directly between Earth and the sun for the first time since 1882. Insignificant though it may seem, this rare celestial event, a “transit of Venus”, was once thought a key to understanding the universe. Two and a half centuries ago, countries dispatched astronomers on risky and expensive expeditions to observe transits from far-flung points across the globe. By doing this, they hoped to make a precise measurement of the distance to the sun and thus acquire an accurate yardstick by which the distance to everything else in the solar system could be measured. Though this quest fell short of its goal, it did produce a much better estimate of that distance. It also produced some interesting spin-offs, such as the invention of the movie camera and the discovery of Australia's Great Barrier Reef. In any case, astronomers—both professional and amateur—are eagerly awaiting the forthcoming transit so that they can commune with the shades of their predecessors.
    [Show full text]
  • PDF Click to View Or Download
    Learning Outcomes in Focus Contextual strand: PW3 Students should be able to investigate patterns and relationships between physical observables. INVESTIGATE: Observe, study or make detailed and systematic examination, in order to establish facts and reach new conclusions Nature of science: NoS1 Students should be able to appreciate how scientists work and how scientific ideas are modified over time. APPRECIATE: Have a practical understanding of Learning Intentions As this activity relates to many learning outcomes, including those above, be sure to decide on the specific Learning intentions you have for your class if they are to engage with this activity. Introduction and Teacher Background Students will use a light sensor at the beginning of this activity. A light sensor is an electronic device used to detect light. They usually consist of a photoelectric cell which converts light energy into electrical energy. (You might see links to PW5 and PW6). While the unit LUX is in fact itself a derived unit (Lumen m-2), it is a measure of the light intensity as perceived by the human eye and so students will explore light intensity in lux as a physical observable and investigate its relationship to distance from a source and varied obstacles. In the second half of this activity students will try to apply what they have learned to analyse data from the NASA Kepler mission. While in the initial part of the activity variation in light intensity was achieved by allowing a pendulum to swing over and back in front of a light source, a similar pattern, including regular drops in light intensity, would also be achieved as a planet rotated around a star.
    [Show full text]