DOCSLIB.ORG

With Caps Lock Key on Type Title

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
With Caps Lock Key on Type Title Comparison Between Familiar and Unfamiliar Driver Performance in a Multi-Lane Roundabout: A Case Study in Athens, Ohio A thesis presented to the faculty of the Russ College of Engineering and Technology of Ohio University In partial fulfillment of the requirements for the degree Master of Science Ashley N. Chucray August 2013 © 2013 Ashley N. Chucray. All Rights Reserved. 2 This thesis titled Comparison Between Familiar and Unfamiliar Driver Performance in a Multi-Lane Roundabout: A Case Study in Athens, Ohio by ASHLEY N. CHUCRAY has been approved for the Department of Civil Engineering and the Russ College of Engineering and Technology by Deborah S. McAvoy Associate Professor of Civil Engineering Dennis Irwin Dean, Russ College of Engineering and Technology 3 ABSTRACT CHUCRAY, ASHLEY N., M.S., August 2013, Civil Engineering Comparison Between Familiar and Unfamiliar Driver Performance in a Multi-Lane Roundabout: A Case Study in Athens, Ohio Director of Thesis: Deborah S. McAvoy A study was conducted in order to compare driver performance based on driver level of familiarity. The location for the study was a multilane roundabout in Athens, Ohio, the gateway to Ohio University’s campus, making this a unique location. Located to the east of the roundabout is a highway system that leads to most large surrounding cities. Two legs were focused on for this study, the leg that leads to the campus and the leg that leads to this highway system. Familiarity was defined by the presence of large university events such as graduation. The measures of effectiveness for this research were approaching speeds, circulating speeds, critical gap, entrance behaviors, and delay. The objective of this study was to determine what effect familiarity has on these measures of effectiveness. The results from this study showed that unfamiliar drivers had a tendency to drive slower for both circulating and approaching speeds than familiar drivers. Familiar and unfamiliar drivers performed the same for critical cap and inappropriate driver behavior. Also, no distinctive results were extracted from the delay parameter due to the calculation of delay not incorporating driver performance. 4 DEDICATION To my parents, Jill and Jerry Chucray, and my sister, Amanda Chucray. For believing in me, helping me through the tough times, and supporting my academic decisions. 5 ACKNOWLEDGMENTS I would like to thank my advisor, Dr. Deborah McAvoy, for seeing my potential and helping me through every step of my college career, both graduate and undergraduate. Without all of her support, academically and emotionally, neither of my degrees would be possible. I would also like to thank all of my committee members for their service and helpful suggestions for improving my thesis. Additionally, I would like to thank all of my fellow co-workers in the Safety and Human Factors Facility for assisting me with the collection, extraction, and analysis of my data. 6 TABLE OF CONTENTS Page Abstract ............................................................................................................................... 3 Dedication ........................................................................................................................... 4 Acknowledgments............................................................................................................... 5 List of Tables ...................................................................................................................... 9 List of Figures ................................................................................................................... 10 Chapter 1: Introduction ..................................................................................................... 11 1.1 Types of Roundabouts ............................................................................................ 12 1.2 When Roundabouts are Ideal .................................................................................. 13 1.3 Advantages of Roundabouts ................................................................................... 15 1.3.1 Cost .................................................................................................................. 15 1.3.2 Pollution ........................................................................................................... 16 1.3.3 Delay ................................................................................................................ 16 1.3.4 Safety ............................................................................................................... 17 1.4 Rationale for This Study ......................................................................................... 19 Chapter 2: Background ..................................................................................................... 21 2.1 Familiarity of Drivers ............................................................................................. 21 2.1.1 How Familiarity is Defined ............................................................................. 21 2.1.2 Public Opinion of Roundabouts ....................................................................... 22 2.1.3 Operational Knowledge ................................................................................... 25 2.2 Capacity and Saturation Levels .............................................................................. 28 2.2.1 Traffic Volume ................................................................................................. 28 2.2.2 Capacity ........................................................................................................... 29 2.2.3 Saturation Level ............................................................................................... 32 2.3 Pedestrian Consideration ........................................................................................ 34 2.3.1 Pedestrians Impacts .......................................................................................... 34 2.3.2 Reduction of Pedestrian Impacts ..................................................................... 35 2.3.3 Omission of Pedestrian Effects ........................................................................ 37 2.4 Delay ....................................................................................................................... 38 7 2.4.1 Control Delay Measurement ............................................................................ 39 2.4.2 Roundabout Effects on Delay .......................................................................... 41 2.5 Approach and Circulating Speed ............................................................................ 42 2.5.1 Speed Measurement ......................................................................................... 42 2.5.2 Roundabout Speeds .......................................................................................... 43 2.6 Vehicle Classification ............................................................................................. 44 2.6.1 Vehicle Classification Determination .............................................................. 44 2.6.2 Behavior Changes Based on Vehicle Types .................................................... 45 2.7 Gap .......................................................................................................................... 45 2.7.1 Gap Acceptance ............................................................................................... 46 2.7.2 Gap Measurement ............................................................................................ 46 2.7.3 Typical Gap Lengths ........................................................................................ 48 2.7.4 Gap Impacts ..................................................................................................... 49 2.8 Sample Size ............................................................................................................. 50 Chapter 3: Site Description ............................................................................................... 52 Chapter 4: Methodology ................................................................................................... 61 4.1 Data Collection and Equipment .............................................................................. 63 4.1.1 Manual Methods .............................................................................................. 63 4.1.2 Pneumatic Tubes .............................................................................................. 63 4.1.3Radar Detector .................................................................................................. 68 4.1.4 Video Camera .................................................................................................. 69 4.2 Sample Size Determination .................................................................................... 74 Chapter 5: Statistical Methodology .................................................................................. 79 5.1 Tests of Normality and Homogeneous Variance .................................................... 81 5.2 Solutions to Problems with Assumptions ............................................................... 83 5.3 One-way ANOVA .................................................................................................. 85 5.4 Post Hoc Tests .......................................................................................................
Load more

Recommended publications
  • Board of Trustees Ohio University
    Board of Trustees Ohio University Minutes June 26, 2009 MINUTES OF THE MEETING OF THE BOARD OF TRUSTEES OF OHIO UNIVERSITY June 26, 2009 Margaret M. Walter Hall, Governance Room Ohio University, Athens Campus THE OHIO UNIVERSITY BOARD OF TRUSTEES MINUTES OF June 26, 2009 MEETING TABLE OF CONTENTS Communications, Petitions and Memorials .............................................................................. 79 Reports • Report from the Chair ............................................................................................... 79 • Report of the President ............................................................................................. 80 • Report of the Executive Vice President and Provost .................................................. 80 University Resources Committee • Fiscal Year 2009-2010 Operating Budget, Resolution 2009 - 3120 .......................... 81 University Academics Committee • Ohio University/University System of Ohio Centers of Excellence, Resolution 2009 - 3121 ............................................................................................................... 82 • Department of Industrial and Systems Engineering Master of Engineering Management, Resolution 2009 - 3122 ...................................................................... 83 • Acceptance of Major and Degree Program Review, Department of Chemical and Biomolecular Engineering, Resolution 2009 – 3123 .......................................... 84 • Appointment to Regional Coordinating Council, Lancaster Campus,
    [Show full text]
  • Download This PDF File
    The Ohio Journal of Volume 116 No. 1 April Program ANSCIENCE INTERNATIONAL MULTIDISCIPLINARY JOURNAL Abstracts The Ohio Journal of SCIENCE Listing Services ISSN 0030-0950 The Ohio Journal of Sciencearticles are listed or abstracted in several sources including: EDITORIAL POLICY AcadSci Abstracts Bibliography of Agriculture General Biological Abstracts The Ohio Journal of Scienceconsiders original contributions from members and non-members of the Academy in all fields of science, Chemical Abstracts technology, engineering, mathematics and education. Submission Current Advances in Ecological Sciences of a manuscript is understood to mean that the work is original and Current Contents (Agriculture, Biology & unpublished, and is not being considered for publication elsewhere. Environmental Sciences) All manuscripts considered for publication will be peer-reviewed. Deep Sea Research and Oceanography Abstracts Any opinions expressed by reviewers are their own, and do not Environment Abstracts represent the views of The Ohio Academy of Science or The Ohio Journal of Science. Environmental Information Center Forest Products Abstracts Forestry Abstracts Page Charges Geo Abstracts Publication in The Ohio Journal of Science requires authors to assist GEOBASE in meeting publication expenses. These costs will be assessed at $50 per page for nonmembers. Members of the Academy do not Geology Abstracts pay page charges to publish in The Ohio Journal of Science. In GeoRef multi-authored papers, the first author must be a member of the Google Scholar Academy at the time of publication to be eligible for the reduced Helminthological Abstracts member rate. Papers that exceed 12 printed pages may be charged Horticulture Abstracts full production costs. Knowledge Bank (The Ohio State University Libraries) Nuclear Science Abstracts Submission Review of Plant Pathology Electronic submission only.
    [Show full text]
  • Board of Trustees Ohio University Athens Campus
    Board of Trustees Ohio University Athens Campus Agenda April 20, 2012 BOARD ACTIVITIES FOR April 19 & 20, 2012 Ohio University – Athens Campus Activity & Committee Meeting Schedule Thursday, April 19, 2012 8:30 a.m. Convene at Margaret M. Walter Hall, Governance Room 9:00 a.m. RCM Overview - “Responsibility Centered Management: A Panel of Experts Discusses RCM Opportunities Offered and Lessons Learned” 11:30 a.m. Lunch, President’s Dining Room, 4th Floor Baker University Center 12:30 p.m. University Academics and Resources Joint Committee Meeting, Margaret M. Walter Hall, Governance Room 104 2:00 p.m. University Resources Committee, Margaret M. Walter Hall, Room 125 2:00 p.m. University Academics Committee, Margaret M. Walter Hall, Governance Room 104 4:30 p.m. Governance Committee, Margaret M. Walter Hall, Room 125 4:30 p.m. Audit Committee, Margaret M. Walter Hall, Room 127 6:30 p.m. Reception – Trustees, President, First Lady, Executive Staff, Board Secretary – 29 Park Place, President’s Residence 7:00 p.m. Dinner – Trustees, President, First Lady, Executive Staff, Board Secretary – 29 Park Place, President’s Residence Friday, April 20, 2012 7:30 a.m. Trustee Breakfast, Executive Committee, Wilson Room, Ohio University Inn 10:00 a.m. Board Meeting, Margaret M. Walter Hall, Governance Room 104 Noon Media Availability, Margaret M. Walter Hall, Room 125 Noon Trustee Luncheon, Margaret M. Walter Hall, Room 127 AGENDA Board of Trustees’ Meeting Friday, April 20, 2012 – 10:00 a.m. Governance Room, Margaret M. Walter Hall, Athens Campus OPEN SESSION Roll Call Approval of Agenda 1.
    [Show full text]
  • 2015 Ohiodance Fall Festival and Conference
    2015 OhioDance Fall Festival and Conference Dance Matters: Moving Forward #ohiodancefest October 23-25, 2015 Special Guest Artist Kyle Abraham Co-sponsored by Ohio University, School of Dance, Film, and Theater, Division of Dance in Athens, Ohio Kyle Abraham Photo by Celeste Sloman Photo Courtesy of Kyle Abraham/AbrahamIn.Motion Photo Courtesy of Ohio University Division of Dance www.ohiodance.org BFA in Choreography and Performance BA in Dance Dance Minors in Choreography DANCE and Performance, Dance History and Theory, and Somatic Studies For more info contact us at: Ohio University Dance Division 137 Putnam Hall • Athens, OH 45701 Office: (740) 593-1826 Fax: (740) 593-0749 Email: [email protected] www.ohio.edu/finearts/dance Photo Credit: Larry Coleman 2 www.ohiodance.org Dance Matters: Moving Forward OhioDance, the leading state-wide organization supporting diverse dance practices, will hold its fall festival October 23-25, 2015. This event is co-hosted by Ohio University, School of Dance, Film, and Theater, Division of Dance in Athens, Ohio. The theme and title of the conference, Dance Matters: Moving Forward, encompasses the idea that no matter what future changes may occur, dance and the arts will always forge ahead creatively, kinesthetically, and intellectually. Special events include Guest Artist Kyle Abraham will offer a master class and lecture. Abraham.In.Motion company members will provide a lecture demonstration. Over the three day weekend there will be a dance performance, a variety of master classes, dance film showings, a regional roundtable centered around the OhioDance Virtual Dance Collection, discussion on social media law and Ohio University dance division faculty will provide information Kyle Abraham about the dance program at OU for PreProfessional dancers as well as an audition by OU faculty for high school seniors.
    [Show full text]
  • Ohio University Undergraduate Catalog 2005-2006
    Ohio University The fees, programs, and requirements contained in this catalog are effective with Undergraduate the 2005 fall quarter. They are necessarily subject to change at the discretion Catalog 2005-2006 of Ohio University. It is the student’s responsibility to know and follow current requirements and procedures at the departmental, College, and University levels. Ohio University is an af fir ma tive Produced by the Office Ohio University (USPS 405-380), Volume action institution. of University Publications CII, Number 2, July 2005. Published Editor: Brian W. Stemen, M.A., ‘98 by Ohio University, University Terrace, Editorial Assistant: Erin L. Stookey, B.S.J., ‘05 Athens, Ohio 45701-2979 in March, Cover Design: Katie E. Ingersoll, B.F.A., ’06 July, August, September, and October. Periodicals Postage Paid at Athens, Copyright 2005 Ohio. Ohio University Communications and Marketing 0136–46M 2 Extended Community Ohio University Mission State ment Ohio University serves an extended community. The public service mission Ohio University is a public uni ver si ty providing a broad range of ed u- of the University, expressed in such ca tion al programs and services. As an academic community, Ohio activities as public broadcasting and University holds the intellectual and personal growth of the in di vid u al to continuing education programs, reflects be a central purpose. Its programs are designed to broaden perspectives, the re spon si bil i ty of the University to enrich awareness, deepen un der stand ing, establish disciplined habits serve the ongoing ed uca tion al needs of thought, prepare for mean ing ful careers and, thus, to help develop of the region.
    [Show full text]
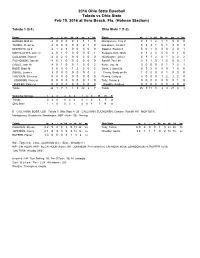
  • 2016 Box Scores
    2016 Ohio State Baseball Toledo vs Ohio State Feb 19, 2016 at Vero Beach, Fla. (Holman Stadium) Toledo 1 (0-1) Ohio State 7 (1-0) Player ab r h rbi bb so po a lob Player ab r h rbi bb so po a lob HANSEN,Matt 2b 4 0 0 0 0 2 1 1 0 Montgomery, Troy cf 4 1 1 2 1 1 5 0 0 TANSEL, Deion ss 4 0 0 0 0 0 2 1 0 Bosiokovic, Jacob rf 5 2 3 1 0 1 3 0 3 MONTOYA, AJ lf 4 1 2 1 0 0 3 0 0 Dawson, Ronnie lf 5 0 1 0 0 0 2 0 1 MARTILLOTTA, John cf 4 0 1 0 0 0 0 0 1 Sergakis, Nick 3b/2b 4 1 2 0 0 0 0 1 0 CALLAHAN, Ryan rf 4 0 2 0 0 0 2 0 0 Washington, Jalen c 4 1 1 2 0 1 5 2 2 ZUCHOWSKI, Dan dh 4 0 1 0 0 0 0 0 0 Ratcliff, Zach dh 3 1 1 0 1 2 0 0 1 CALES, Josh 1b 4 0 1 0 0 1 5 0 2 Kuhn, Troy 1b 3 0 0 0 0 1 7 2 1 BOSS, Brad 3b 3 0 0 0 1 2 2 0 2 Davis, L Grant 2b 3 1 2 0 0 0 1 0 0 SOKOL, Lucas c 3 0 0 0 0 0 9 0 2 Cherry, Brady ph/3b 1 0 0 0 0 1 0 0 0 CALHOUN, Steven p 0 0 0 0 0 0 0 0 0 Nennig, Craig ss 3 0 0 0 1 2 2 2 0 JOHNSON, Casey p 0 0 0 0 0 0 0 1 0 Tully, Tanner p 0 0 0 0 0 0 0 1 0 RUFFER, Parker p 0 0 0 0 0 0 0 0 0 Woodby, Austin p 0 0 0 0 0 0 2 0 0 Totals 34 1 7 1 1 5 24 3 7 Totals 35 7 11 5 3 9 27 8 8 Score by Innings 1 2 3 4 5 6 7 8 9 R H E Toledo 0 0 0 0 0 0 0 1 0 1 7 2 Ohio State 1 1 0 0 3 2 0 0 X 7 11 0 E - CALLAHAN; BOSS.
    [Show full text]
  • Board of Trustees Ohio University Chillicothe, Ohio
    Board of Trustees Ohio University Chillicothe, Ohio Agenda June 21, 22, 2018 BOARD ACTIVITIES Ohio University, Chillicothe, Ohio Activity & Committee Meeting Schedule June 21, 22, 2018 Thursday, June 21, 2018 8:00 am Executive Committee, Bennett Hall Room 110 Executive Session ~10:00 am Academics and Student Success Committee (upon completion of prior meeting – Bennett Hall Room 110 12:30 pm Lunch with Dean of OU-C – Art Gallery 1:45 pm Resources, Finance, and Affordability Committee – Bennett Hall Room 110 ~4:45 pm Audit and Risk Management Committee (upon completion of prior meeting) – Bennett Hall Room 110 7:00 pm Dinner – Trustees, President, President’s Council, Board Secretary, Faculty Representatives, Dean invitees Friday, June 22, 2018 8:15 am Morning tour – Bennett Hall Room 110 9:00 am Executive Committee– Bennett Hall Room 110 Executive Session 10:00 am Governance and Compensation Committee – Bennett Hall Room 110 10:45 am Main Board Meeting 12:45 pm Trustee Luncheon – Bennett Hall Room 105 12:45 pm Media Availability – Bennett Hall Room 102 Committee Agendas AGENDA Board of Trustees Meeting Chillicothe Campus, Bennett Hall 110 Friday, June 22, 2018, 10:45am Roll Call Approval of Agenda Tab 1 Approval of Minutes: Board of Trustees’ Meetings of March 23, 2018 and May 14, 2018 Comments from the Chair of the Board of Trustees Tab 2 - Report from the President Shared Governance Discussion Committee Information Items and Resolutions • University Resources, Facilities, and Affordability Committee • University Academics and Student Success Committee • Governance and Compensation Committee • Audit and Risk Management Committee • Executive Committee Consent Agenda Any trustee may request, in advance of action on the consent agenda, that any matter set out in this consent agenda be removed and placed on the regular agenda for discussion and action.
    [Show full text]
  • South Green College Green East Green Hdl Center West
    HDL CENTER MC 150 33 MC 148 150 149 147 M Apartment Parking Only 50 M 145 TRANSPORTATION AND PARKING 153 SERVICES 109 MC MC 40 Apartment Parking Only 39 143 20 18 41 109 M 38 36 37 19 M 110 MC 116 43 MC 43 111 115 125 WEST GREEN 119 44 Golf Course ...................................73 H-7 M COLLEGE GREEN Gordy.............................................84 G-5 M 50 Graduate Services Office ................3 G-4 EAST GREEN Grosvenor......................................96 D-4 112 Grosvenor, West Wing................119 D-4 Grounds Maintenance..................88 G-6 P2P GRG Grover............................................89 E-5 O.U. COM M Guest Housing (Scott)...................76 H-5 PATIENT 114 M 104 Guest/Visitor Parking....................56 H-4 PARKING 122 Haning...........................................20 F-3 M RIVER HDL Center...................................142 E-1 11 PARK Health and Human Services, MC M College Office .............................96 D-4 M TOWERS Heating Plant ..............................108 C-3 Heating Substation.......................23 F-3 Honors Tutorial, College Office ...83 G-5 112 Hoover.........................................136 I-7 M Howard Park ...............................143 I-3 M 120 128 128 Hudson ..........................................35 H-3 M Human Resources CAMPUS POLICE and Training Center...................150 E-1 51 Innovation Center.......................154 C-1 2 6 Intramural Field ..........................116 L-3 52 54 Irvine............................................102 E-4 55 55 James 97 E-5 129 53 Jefferson........................................46 I-4 MC M MC MC Jennings ........................................37 H-3 128 Johnson .........................................47 I-4 MC M Kantner .........................................30 H-2 203 3 M 90 Kennedy Museum.......................201 C-7 4 Konneker Alumni Center .............60 H-5 128 Konneker Research Labs ............225 B-5 MC Alphabetical Index Bldg.
    [Show full text]
  • A Bulleted/Pictorial History of Ohio University
    A Bulleted/Pictorial History of Ohio University Dr. Robert L. Williams II (BSME OU 1984), Professor Mechanical Engineering, Ohio University © 2020 Dr. Bob Productions [email protected] www.ohio.edu/mechanical-faculty/williams Ohio University’s Cutler Hall, 1818, National Historical Landmark ohio.edu/athens/bldgs/cutler Ohio University’s College Edifice flanked by East and West Wings circa 1840 (current Cutler Hall flanked by Wilson and McGuffey Halls) ohiohistorycentral.org 2 Ohio University History, Dr. Bob Table of Contents 1. GENERAL OHIO UNIVERSITY HISTORY .................................................................................. 3 1.1 1700S ................................................................................................................................................. 3 1.2 1800S ................................................................................................................................................. 4 1.3 1900S ............................................................................................................................................... 13 1.4 2000S ............................................................................................................................................... 42 1.5 OHIO UNIVERSITY PRESIDENTS ........................................................................................................ 44 2. OHIO UNIVERSITY ENGINEERING COLLEGE HISTORY .................................................. 50 2.1 OHIO UNIVERSITY ENGINEERING HISTORY,
    [Show full text]
  • Request for Proposal
    THE INTER-UNIVERSITY COUNCIL PURCHASING GROUP REQUEST FOR PROPOSAL Date Issued: 2/23/2010 Due Date/Time: 3/19/2010 @ 3:00 P.M., Local Time RFP: UN10-081 IUC-PG Bleacher Inspection Services Proposals must be received, by the due date/time specified above at the location below. Proposals received after the due date/time will not be opened and will be returned to the vendor, if requested. For proposals delivered via the U.S. Mail, please use the U. S. Mail Address shown below: U. S. Mail Address: Contact: INQUIRY #UN10-081 Kent State University Larry McWilliams, C.P.M. Procurement Department Interim Director, Procurement Attn: Larry McWilliams 229 Schwartz Center Email: [email protected] 800 Summit Street PO Box 5190 Kent, Ohio 44242 Phone: 330-672-9196 FAX: 330-673-7904 By signing this document I am agreeing, on behalf of my firm, to the specifications of this RFP and accepting, without exception or amendment, the IUC-PG’s Standard RFP Agreement Terms (Section III). All purchase orders resulting from this RFP shall be subject to these instructions, terms and requirements that shall be incorporated therein.1 Submitted by: Company H&H Enterprises, Inc. Authorized Signature ____________________________Date_____________________ ____________________________ _______________________ 1 Should a bidder take exception to the IUC-PG’s Standard RFP Agreement Terms (Section III cited above) the bidder must submit such exceptions and/or amendments in writing to the contact above within five (5) business days prior to the Proposal Closing Date. The IUC-PG reserves the right to reject some, all or none of the proposed exceptions and/or amendments and asserts its Standard RFP Agreement Terms as described in Sections III.
    [Show full text]
  • Board of Trustees Ohio University Athens, Ohio
    Board of Trustees Ohio University Athens, Ohio Agenda November 1, 2013 BOARD ACTIVITIES FOR October 31st & November 1st, 2013 Ohio University Main Campus – Athens, Ohio Activity & Committee Meeting Schedule Thursday, October 31, 2013 8:20 a.m. Bus pick-up to President’s Residence, Margaret M. Walter Hall Parking Lot 8:30 a.m. Breakfast & Group/Individual Photos, 29 Park Place; Photographer Ben Siegel 9:30 a.m. Tour of the President’s Residence, 29 Park Place 10:45 a.m. Joint Committee Meetings: Academics and Resources, Margaret M. Walter Hall, Governance Room 12:30 p.m. Trustee Luncheon & Joint Committee Meeting, Margaret M. Walter Hall Rotunda, 1:30 p.m. Resources Committee, Margaret M. Walter Hall, Governance Room 104 1:30 p.m. Academics Committee, Margaret M. Walter Hall, Room 125/127 3:30 p.m. Governance Committee, Margaret M. Walter Hall, Room 125 3:30 p.m. Audit Committee, Margaret M. Walter Hall, Room 127 6:30 p.m. Reception – Trustees, President, Board Secretary, Executive Staff and Guests; OU Inn, Lindley Room 7 p.m. Dinner – Trustees, President, Board Secretary, Executive Staff and Guests; OU Inn, Lindley Room Friday, November 1, 2013 7:30 a.m. Trustee Breakfast - Executive Committee; OU Inn, Lindley Room 10 a.m. Board Meeting; Margaret M. Walter Hall, Governance Room 104 Noon Trustee Luncheon, Margaret M. Walter Hall 125 Noon Media Availability, Margaret M. Walter Hall 127 AGENDA Board of Trustees Meeting Friday, November 1, 2013 – 10:00 a.m. Margaret M. Walter Hall, Governance Room 104-Athens Campus OPEN SESSION Roll Call Approval of Agenda 1.
    [Show full text]
  • Board of Trustees Ohio University Athens, Ohio
    Board of Trustees Ohio University Athens, Ohio Agenda August 22-23, 2017 BOARD ACTIVITIES for August 22, 2017 Dublin Campus - Dublin Integrated Education Center Activity & Committee Meeting Schedule *Times are approximate Tuesday, August 22, 2017 7:45 a.m. Meet at the Dublin Campus, Dublin Integrated Education Center, 6805 Bobcat Way, Dublin, Ohio Ongoing Trustee Hospitality/Break Room, Room 249 8:00 a.m. Executive Committee – Room 249 9:00 a.m. Governance Committee, Room 246/247 9:00 a.m. Audit Committee, Room 245 10:00 a.m. Joint Committee Meeting, Room 246/247 12:00 p.m. Trustee Luncheon & Updates Trustees, President, Board Secretary, President’s Council, Faculty Reps, Faculty Senate Chair Room 249 1:00 p.m. University Resources Committee, Room 246/247 1:00 p.m. University Academics Committee, Room 245 3:00 p.m. Board Meeting, Room 246/247 5:00 p.m. Media Availability, Room 251 6:15 p.m. Bus will leave for dinner from Hotel to dinner 6:30 p.m. Reception – Trustees, President, President’s Council and Board Secretary 7:00 p.m. Dinner – Trustees, President, President’s Council and Board Secretary BOARD ACTIVITIES FOR August 23, 2017 Dublin Campus - Dublin Integrated Education Center Activity & Committee Meeting Schedule *Times are approximate Retreat Schedule Wednesday, August 23, 2017 7:45 a.m. Meet at the Dublin Campus, Dublin Integrated Education Center, 6805 Bobcat Way, Dublin, Ohio Ongoing Hospitality/Break, Room 249 8:00 a.m. Executive Committee, Room 249 9:30am Break 9:45 a.m. Welcome – Chair King, President Nellis Room 246/247 10:00 am Trustee Workshop: Trustees, President Nellis, President’s Council, Room 246/247 12:00 p.m.
    [Show full text]