DOCSLIB.ORG

NOTES on COMPLEX VARIABLES 1. the Complex Exponential

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
NOTES on COMPLEX VARIABLES 1. the Complex Exponential NOTES ON COMPLEX VARIABLES 1. The complex Exponential Function ez, where z = x + iy The complex exponential function is defined by extending the Taylor series of ex from real values of x to complex values: ez =1+ z + z2/2+ z3/3! + ... (1) The partial sums are well defined since products and sums of complex numbers are well defined. With this definition, ez agrees with ex when z is real. Furthermore, one can show that ez satisfies z1 z1+z2 z1 z2 z1−z2 e z n nz d z z the properties of exponentials: e = e e , e = ez2 , (e ) = e , dz [e ]= e . We showed in class that the definition (1) implies Euler’s formula: if θ is a real number, then eiθ = cos θ + i sin θ (2) which is a point on the unit circle that subtends an angle θ with the real axis. Every complex number z in the complex plane is obtained by taking a point on the unit circle times its magnitude r. Thus, Euler’s formula enables us to write any complex number z = x + iy in the form z = reiθ = r cos(θ)+ ir sin(θ) (3) where r is the modulus and θ is the argument. We’ll refer to this form as the polar representation of z in terms of the coordinates r, θ. The relation between the polar representation z = reiθ and the Cartesian representation z = x + iy can be seen from (3) to be given by x = r cos θ, y = r sin θ and r = x2 + y2,θ = atan(y/x) . p By writing complex numbers in polar form it is easy to take powers and roots of complex numbers, as shown in the following examples. Example 1: Plot the complex number 1+ i in the complex plane and find its polar representation. Solution: By plotting the point we see that θ = π/4 and r = √2. Thus 1 + i = √2eiπ/4. Example 2: Find the real and imaginary parts of z = (1+ i)10. Solution: We use the polar representation 1 + i = √2eiπ/4 and the properties of the exponential function to find that 10 π 10 5 5π 5 π 5 z = (1+ i) =(√2ei 4 ) = 2 ei 2 = 2 ei 2 = 2 i so Re(z)=0, Im(x) = 25. That is, z = (1+ i)10 = 32i. Notice that taking a complex number z = reiθ to a power zn = rneinθ 1 simply takes the power of the modulus and multiplies the argument by n. For example squaring a number squares the modulus and doubles the argument. Exercise: Plot all integer powers of the complex number on the unit circle (1+ i)/√2. Euler’s formula also enables us to identify the real and imaginary parts of ez, where z = x + iy, as follows ez = ex+iy = exeiy = ex(cos y + i sin y)= ex cos y + iex sin y . (4) so Re(z)= ex cos y and Im(z)= ex sin y. Example 3: Find the real and imaginary parts of z = e1+i . Solution: z = e1+i = e1ei = e(cos1 + i sin1), so Re(z)= e cos1 and Im(z)= e sin1. Note that the argument of a complex number is not uniquely defined since you can add any multiple 2nπ of 2π, where n is any positive or negative integer, to θ and get the same points. That is, if z = reiθ then also z = rei(θ+2nπ) For example, the number 1 = e0i = e(0+2nπ)i = e2nπi. We’ll use this to find all complex roots of equations. In particular, all roots of unity. Example 4: Find all complex roots of z3 = 1. Note: The fundamental theorem of algebra states that a polynomial of degree n has precisely n complex roots, possibly repeated. This implies that z3 1 = 0 has precisely 3 complex roots. − Solution: By taking the modulus on both sides we find that z3 = z 3 =1 so z =1 so z must be a point on the unit circle, | | | | | | z = eiθ By plugging this into the equation and writing 1 = e2nπi we get that ei3θ = e2nπi Now we can equate powers to get for n =0: θ = 0 for n =1: θ = 2π/3 for n =2: θ = 4π/3 Any other values of n only give values of θ that agree with one of the above to within a multiple of 2π. So the 3 distinct cubic roots of unity are 2π 4π z = 1,e 3 i,e 3 i . Alternatively, one can think of this problem as follows: we want to find a number z such that the 3 i2π/3 argument of z is 2π. Since cubing it triples the argument of z we deduce that z0 = e is a 3 2 3 j solution. Since z0 = 1 it follows that any power z0 , z0 , ... , z0, ... , also solve the equation, since j 3 3 j j they satisfy (z0) = (z0 ) = 1 = 1. You can check that only 3 of those powers are distinct. z0 is called the principal root of unity. 2 2. Deriving Trig identities using Euler’s Formula Euler’s formula and the properties of exponentials make it is easy to derive several of the trigono- metric identities we have been using. Example 10: Use exponentials to derive formulas for sin2x and cos 2x. Solution: Start with the identity e2ix =(eix)2. Using Euler’s formula we rewrite this identity as cos 2x + i sin2x = (cos x + i sin x)2 = cos2 x sin2 x + 2i sin x cos x − By equating real and imaginary parts on the left and right hand side of this equation we get cos 2x = cos2 x sin2 x , sin2x = 2sin x cos x − 3. Integration using Complex Variables Complex variables can also be used to determine integrals that are tedious to evaluate using conven- tional methods. For example, consider integrals of the form eat cos bt dt. Recall how to integrate using integration by parts. Here it is shown that the use of coRmplex variables can sometimes reduce the complecity of the integration of such functions. You will need to use Euler’s equation and the definition of equality for complex numbers – namely that if z1 = z2 then Re(z1) = Re(z2) and Im(z1)= Im(z2). We first define what the integral of a complex function means. Consider a complex valued function w(t)= u(t)+ iv(t), where u and v are real-valued function and t is a real variable. (That is, u and v are the real and imaginary parts of w.) Then the integral of w is defined by b b b w(t)dt = u(t)dt + i v(t)dt (10) Za Za Za 1 2 Example 11: Evaluate the integral 0 1 + 2it dt Solution: 1 2 1 R 1 2 1 3 1 0 1 + 2it dt = 0 1 dt + 2i 0 t dt =[t]0 + 2i t /3 0 =1+2i/3 R R R It follows that the standard rules of integration can be used by treating i as a constant. π/3 2it Example 12: Evaluate the integral 0 e dt π/3 Solution: π/3 e2itdt = 1 e2it =R 1 e2iπ/3 e0 = −i 3/2+ i√3/2 = √3/4 + 3i/4 0 2i 0 2i − 2 − We nowR illustrate that some of the integrals we computed earlier this semester are evaluated quite easily if we use complex variables instead. Example 13: Evaluate the integral e(a+ib)tdt. What do you learn by equating real and imaginary parts on the left and rightR hand sides of the resulting equation? 1 Solution: e(a+ib)tdt = e(a+ib)t + C . Equating real and imaginary parts gives Z a + ib at at e e cos bt dt = (a cos bt + b sin bt)+ C1 , Z a2 + b2 at at e e sin bt dt = (a sin bt b cos bt)+ C2 , Z a2 + b2 − 3 Notice that to compute these two integrals without complex variables, we would have to use integration by parts twice. These integrals occur frequently in mechanical systems. The functions eat cos bt, eat sin bt represent oscillating functions whose magnitude grows or decays exponentially. Problems: Part I Powers of complex numbers: 1. Write the following numbers in the form reiθ and in the form a+ib: (a) (1+i)20, (b) (1 √3i)5, (c) (2√3 + 2i)5, (d) (1 i)8. − − 2. Find all solutions to the given equation. Sketch the roots in the complex plane. (a) z8 = 1 (the eigth roots of unity) (b) z5 = 1 (the fifth roots of unity) (c) z5 = 32 (the fifth roots of 32) Problems: Part II Exponentials and Logarithms: πi 2±3πi 2 2+ e z+πi z 1. Show that: (a) e = e (b) e 4 = (1 + i) (c) e = e − 2 − p 2. Find the real and imaginary parts of e(2−3i)t (t is real) Trigonometric Identities: 3. Derive the formulas for sin(a + b) and cos(a + b) using complex variables. (Hint: look at the real and imaginary parts of the equation ei(a+b) = eiaeib.) Integration: 4. Evaluate the following integrals 1 2 π/4 it (a) 0 (1 + it ) dt (b) 0 e dt 5. FindR the indefinite integralR e−st cos(at) dt, where s,a are positive constants (a) using integration by partsR twice (b) by integrating e−steiat dt, and then equating real and imaginary parts. 6. The Laplace transformR of a function f(t) is defined to be ∞ F (s)= [f](t)= e−stf(t) dt L Z0 (a) Find the Laplace transform of f(t) = cos(at).
Load more

Recommended publications
  • Integration in the Complex Plane (Zill & Wright Chapter
    Integration in the Complex Plane (Zill & Wright Chapter 18) 1016-420-02: Complex Variables∗ Winter 2012-2013 Contents 1 Contour Integrals 2 1.1 Definition and Properties . 2 1.2 Evaluation . 3 1.2.1 Example: R z¯ dz ............................. 3 C1 1.2.2 Example: R z¯ dz ............................. 4 C2 R 2 1.2.3 Example: C z dz ............................. 4 1.3 The ML Limit . 5 1.4 Circulation and Flux . 5 2 The Cauchy-Goursat Theorem 7 2.1 Integral Around a Closed Loop . 7 2.2 Independence of Path for Analytic Functions . 8 2.3 Deformation of Closed Contours . 9 2.4 The Antiderivative . 10 3 Cauchy's Integral Formulas 12 3.1 Cauchy's Integral Formula . 12 3.1.1 Example #1 . 13 3.1.2 Example #2 . 13 3.2 Cauchy's Integral Formula for Derivatives . 14 3.3 Consequences of Cauchy's Integral Formulas . 16 3.3.1 Cauchy's Inequality . 16 3.3.2 Liouville's Theorem . 16 ∗Copyright 2013, John T. Whelan, and all that 1 Tuesday 18 December 2012 1 Contour Integrals 1.1 Definition and Properties Recall the definition of the definite integral Z xF X f(x) dx = lim f(xk) ∆xk (1.1) ∆xk!0 xI k We'd like to define a similar concept, integrating a function f(z) from some point zI to another point zF . The problem is that, since zI and zF are points in the complex plane, there are different ways to get between them, and adding up the value of the function along one path will not give the same result as doing it along another path, even if they have the same endpoints.
    [Show full text]
  • Niobrara County School District #1 Curriculum Guide
    NIOBRARA COUNTY SCHOOL DISTRICT #1 CURRICULUM GUIDE th SUBJECT: Math Algebra II TIMELINE: 4 quarter Domain: Student Friendly Level of Resource Academic Standard: Learning Objective Thinking Correlation/Exemplar Vocabulary [Assessment] [Mathematical Practices] Domain: Perform operations on matrices and use matrices in applications. Standards: N-VM.6.Use matrices to I can represent and Application Pearson Alg. II Textbook: Matrix represent and manipulated data, e.g., manipulate data to represent --Lesson 12-2 p. 772 (Matrices) to represent payoffs or incidence data. M --Concept Byte 12-2 p. relationships in a network. 780 Data --Lesson 12-5 p. 801 [Assessment]: --Concept Byte 12-2 p. 780 [Mathematical Practices]: Niobrara County School District #1, Fall 2012 Page 1 NIOBRARA COUNTY SCHOOL DISTRICT #1 CURRICULUM GUIDE th SUBJECT: Math Algebra II TIMELINE: 4 quarter Domain: Student Friendly Level of Resource Academic Standard: Learning Objective Thinking Correlation/Exemplar Vocabulary [Assessment] [Mathematical Practices] Domain: Perform operations on matrices and use matrices in applications. Standards: N-VM.7. Multiply matrices I can multiply matrices by Application Pearson Alg. II Textbook: Scalars by scalars to produce new matrices, scalars to produce new --Lesson 12-2 p. 772 e.g., as when all of the payoffs in a matrices. M --Lesson 12-5 p. 801 game are doubled. [Assessment]: [Mathematical Practices]: Domain: Perform operations on matrices and use matrices in applications. Standards:N-VM.8.Add, subtract and I can perform operations on Knowledge Pearson Alg. II Common Matrix multiply matrices of appropriate matrices and reiterate the Core Textbook: Dimensions dimensions. limitations on matrix --Lesson 12-1p. 764 [Assessment]: dimensions.
    [Show full text]
  • 1 the Complex Plane
    Math 135A, Winter 2012 Complex numbers 1 The complex numbers C are important in just about every branch of mathematics. These notes present some basic facts about them. 1 The Complex Plane A complex number z is given by a pair of real numbers x and y and is written in the form z = x+iy, where i satisfies i2 = −1. The complex numbers may be represented as points in the plane, with the real number 1 represented by the point (1; 0), and the complex number i represented by the point (0; 1). The x-axis is called the \real axis," and the y-axis is called the \imaginary axis." For example, the complex numbers 1, i, 3 + 4i and 3 − 4i are illustrated in Fig 1a. 3 + 4i 6 + 4i 2 + 3i imag i 4 + i 1 real 3 − 4i Fig 1a Fig 1b Complex numbers are added in a natural way: If z1 = x1 + iy1 and z2 = x2 + iy2, then z1 + z2 = (x1 + x2) + i(y1 + y2) (1) It's just vector addition. Fig 1b illustrates the addition (4 + i) + (2 + 3i) = (6 + 4i). Multiplication is given by z1z2 = (x1x2 − y1y2) + i(x1y2 + x2y1) Note that the product behaves exactly like the product of any two algebraic expressions, keeping in mind that i2 = −1. Thus, (2 + i)(−2 + 4i) = 2(−2) + 8i − 2i + 4i2 = −8 + 6i We call x the real part of z and y the imaginary part, and we write x = Re z, y = Im z.(Remember: Im z is a real number.) The term \imaginary" is a historical holdover; it took mathematicians some time to accept the fact that i (for \imaginary," naturally) was a perfectly good mathematical object.
    [Show full text]
  • Complex Eigenvalues
    Quantitative Understanding in Biology Module III: Linear Difference Equations Lecture II: Complex Eigenvalues Introduction In the previous section, we considered the generalized two- variable system of linear difference equations, and showed that the eigenvalues of these systems are given by the equation… ± 2 4 = 1,2 2 √ − …where b = (a11 + a22), c=(a22 ∙ a11 – a12 ∙ a21), and ai,j are the elements of the 2 x 2 matrix that define the linear system. Inspecting this relation shows that it is possible for the eigenvalues of such a system to be complex numbers. Because our plants and seeds model was our first look at these systems, it was carefully constructed to avoid this complication [exercise: can you show that http://www.xkcd.org/179 this model cannot produce complex eigenvalues]. However, many systems of biological interest do have complex eigenvalues, so it is important that we understand how to deal with and interpret them. We’ll begin with a review of the basic algebra of complex numbers, and then consider their meaning as eigenvalues of dynamical systems. A Review of Complex Numbers You may recall that complex numbers can be represented with the notation a+bi, where a is the real part of the complex number, and b is the imaginary part. The symbol i denotes 1 (recall i2 = -1, i3 = -i and i4 = +1). Hence, complex numbers can be thought of as points on a complex plane, which has real √− and imaginary axes. In some disciplines, such as electrical engineering, you may see 1 represented by the symbol j. √− This geometric model of a complex number suggests an alternate, but equivalent, representation.
    [Show full text]
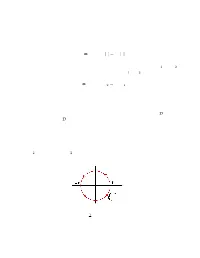
  • The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs in first Year Calculus You Learned About the Formula: Z B 1 Dx = Ln |B| − Ln |A| a X
    The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs In first year calculus you learned about the formula: Z b 1 dx = ln jbj ¡ ln jaj a x It is natural to want to apply this formula to contour integrals. If z1 and z2 are complex numbers and C is a path connecting z1 to z2, we would expect that: Z 1 dz = log z2 ¡ log z1 C z However, you are about to see that there is an interesting complication when we take the formula for the integral resulting in logarithm and try to extend it to the complex case. First of all, recall that if f(z) is an analytic function on a domain D and C is a closed loop in D then : I f(z) dz = 0 This is referred to as the Cauchy-Integral Theorem. So, for example, if C His a circle of radius r around the origin we may conclude immediately that 2 2 C z dz = 0 because z is an analytic function for all values of z. H If f(z) is not analytic then C f(z) dz is not necessarily zero. Let’s do an 1 explicit calculation for f(z) = z . If we are integrating around a circle C centered at the origin, then any point z on this path may be written as: z = reiθ H 1 iθ Let’s use this to integrate C z dz. If z = re then dz = ireiθ dθ H 1 Now, substitute this into the integral C z dz.
    [Show full text]
  • Complex Sinusoids Copyright C Barry Van Veen 2014
    Complex Sinusoids Copyright c Barry Van Veen 2014 Feel free to pass this ebook around the web... but please do not modify any of its contents. Thanks! AllSignalProcessing.com Key Concepts 1) The real part of a complex sinusoid is a cosine wave and the imag- inary part is a sine wave. 2) A complex sinusoid x(t) = AejΩt+φ can be visualized in the complex plane as a vector of length A that is rotating at a rate of Ω radians per second and has angle φ relative to the real axis at time t = 0. a) The projection of the complex sinusoid onto the real axis is the cosine A cos(Ωt + φ). b) The projection of the complex sinusoid onto the imaginary axis is the cosine A sin(Ωt + φ). AllSignalProcessing.com 3) The output of a linear time invariant system in response to a com- plex sinusoid input is a complex sinusoid of the of the same fre- quency. The system only changes the amplitude and phase of the input complex sinusoid. a) Arbitrary input signals are represented as weighted sums of complex sinusoids of different frequencies. b) Then, the output is a weighted sum of complex sinusoids where the weights have been multiplied by the complex gain of the system. 4) Complex sinusoids also simplify algebraic manipulations. AllSignalProcessing.com 5) Real sinusoids can be expressed as a sum of a positive and negative frequency complex sinusoid. 6) The concept of negative frequency is not physically meaningful for real data and is an artifact of using complex sinusoids.
    [Show full text]
  • COMPLEX EIGENVALUES Math 21B, O. Knill
    COMPLEX EIGENVALUES Math 21b, O. Knill NOTATION. Complex numbers are written as z = x + iy = r exp(iφ) = r cos(φ) + ir sin(φ). The real number r = z is called the absolute value of z, the value φ isjthej argument and denoted by arg(z). Complex numbers contain the real numbers z = x+i0 as a subset. One writes Re(z) = x and Im(z) = y if z = x + iy. ARITHMETIC. Complex numbers are added like vectors: x + iy + u + iv = (x + u) + i(y + v) and multiplied as z w = (x + iy)(u + iv) = xu yv + i(yu xv). If z = 0, one can divide 1=z = 1=(x + iy) = (x iy)=(x2 + y2). ∗ − − 6 − ABSOLUTE VALUE AND ARGUMENT. The absolute value z = x2 + y2 satisfies zw = z w . The argument satisfies arg(zw) = arg(z) + arg(w). These are direct jconsequencesj of the polarj represenj j jtationj j z = p r exp(iφ); w = s exp(i ); zw = rs exp(i(φ + )). x GEOMETRIC INTERPRETATION. If z = x + iy is written as a vector , then multiplication with an y other complex number w is a dilation-rotation: a scaling by w and a rotation by arg(w). j j THE DE MOIVRE FORMULA. zn = exp(inφ) = cos(nφ) + i sin(nφ) = (cos(φ) + i sin(φ))n follows directly from z = exp(iφ) but it is magic: it leads for example to formulas like cos(3φ) = cos(φ)3 3 cos(φ) sin2(φ) which would be more difficult to come by using geometrical or power series arguments.
    [Show full text]
  • Complex Analysis
    Complex Analysis Andrew Kobin Fall 2010 Contents Contents Contents 0 Introduction 1 1 The Complex Plane 2 1.1 A Formal View of Complex Numbers . .2 1.2 Properties of Complex Numbers . .4 1.3 Subsets of the Complex Plane . .5 2 Complex-Valued Functions 7 2.1 Functions and Limits . .7 2.2 Infinite Series . 10 2.3 Exponential and Logarithmic Functions . 11 2.4 Trigonometric Functions . 14 3 Calculus in the Complex Plane 16 3.1 Line Integrals . 16 3.2 Differentiability . 19 3.3 Power Series . 23 3.4 Cauchy's Theorem . 25 3.5 Cauchy's Integral Formula . 27 3.6 Analytic Functions . 30 3.7 Harmonic Functions . 33 3.8 The Maximum Principle . 36 4 Meromorphic Functions and Singularities 37 4.1 Laurent Series . 37 4.2 Isolated Singularities . 40 4.3 The Residue Theorem . 42 4.4 Some Fourier Analysis . 45 4.5 The Argument Principle . 46 5 Complex Mappings 47 5.1 M¨obiusTransformations . 47 5.2 Conformal Mappings . 47 5.3 The Riemann Mapping Theorem . 47 6 Riemann Surfaces 48 6.1 Holomorphic and Meromorphic Maps . 48 6.2 Covering Spaces . 52 7 Elliptic Functions 55 7.1 Elliptic Functions . 55 7.2 Elliptic Curves . 61 7.3 The Classical Jacobian . 67 7.4 Jacobians of Higher Genus Curves . 72 i 0 Introduction 0 Introduction These notes come from a semester course on complex analysis taught by Dr. Richard Carmichael at Wake Forest University during the fall of 2010. The main topics covered include Complex numbers and their properties Complex-valued functions Line integrals Derivatives and power series Cauchy's Integral Formula Singularities and the Residue Theorem The primary reference for the course and throughout these notes is Fisher's Complex Vari- ables, 2nd edition.
    [Show full text]
  • Complex Numbers Sigma-Complex3-2009-1 in This Unit We Describe Formally What Is Meant by a Complex Number
    Complex numbers sigma-complex3-2009-1 In this unit we describe formally what is meant by a complex number. First let us revisit the solution of a quadratic equation. Example Use the formula for solving a quadratic equation to solve x2 10x +29=0. − Solution Using the formula b √b2 4ac x = − ± − 2a with a =1, b = 10 and c = 29, we find − 10 p( 10)2 4(1)(29) x = ± − − 2 10 √100 116 x = ± − 2 10 √ 16 x = ± − 2 Now using i we can find the square root of 16 as 4i, and then write down the two solutions of the equation. − 10 4 i x = ± =5 2 i 2 ± The solutions are x = 5+2i and x =5-2i. Real and imaginary parts We have found that the solutions of the equation x2 10x +29=0 are x =5 2i. The solutions are known as complex numbers. A complex number− such as 5+2i is made up± of two parts, a real part 5, and an imaginary part 2. The imaginary part is the multiple of i. It is common practice to use the letter z to stand for a complex number and write z = a + b i where a is the real part and b is the imaginary part. Key Point If z is a complex number then we write z = a + b i where i = √ 1 − where a is the real part and b is the imaginary part. www.mathcentre.ac.uk 1 c mathcentre 2009 Example State the real and imaginary parts of 3+4i.
    [Show full text]
  • On Bounds of the Sine and Cosine Along Straight Lines on the Complex Plane
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 19 September 2018 doi:10.20944/preprints201809.0365.v1 Peer-reviewed version available at Acta Universitatis Sapientiae, Mathematica 2019, 11, 371-379; doi:10.2478/ausm-2019-0027 ON BOUNDS OF THE SINE AND COSINE ALONG STRAIGHT LINES ON THE COMPLEX PLANE FENG QI Institute of Mathematics, Henan Polytechnic University, Jiaozuo, Henan, 454010, China College of Mathematics, Inner Mongolia University for Nationalities, Tongliao, Inner Mongolia, 028043, China Department of Mathematics, College of Science, Tianjin Polytechnic University, Tianjin, 300387, China E-mail: [email protected], [email protected] URL: https: // qifeng618. wordpress. com Abstract. In the paper, the author discusses and computes bounds of the sine and cosine along straight lines on the complex plane. 1. Motivations In the theory of complex functions, the sine and cosine on the complex plane C are denoted and defined by eiz − e−iz e−iz + e−iz sin z = and cos z = ; 2i 2 where z = x + iy and x; y 2 R. When z = x 2 R, these two functions become sin x and cos x which satisfy the periodicity and boundedness sin(x + 2kπ) = sin x; cos(x + 2kπ) = cos x; j sin xj ≤ 1; j cos xj ≤ 1 for k 2 Z. On the other hand, when z = iy for y 2 R, e−y − ey e−y + ey sin(iy) = ! ±i1 and cos(iy) = ! +1 2i 2 as y ! ±∞. These imply that the sine and cosine are bounded on the real x-axis, but unbounded on the imaginary y-axis. Motivated by the above boundedness, we naturally guess that the complex func- tions sin z and cos z for z 2 C are (1) bounded on all straight lines parallel to the real x-axis, (2) unbounded on all straight lines whose slopes are not horizontal.
    [Show full text]
  • 1 Last Time: Complex Eigenvalues
    MATH 2121 | Linear algebra (Fall 2017) Lecture 19 1 Last time: complex eigenvalues Write C for the set of complex numbers fa + bi : a; b 2 Rg. Each complex number is a formal linear combination of two real numbers a + bi. The symbol i is defined as the square root of −1, so i2 = −1. We add complex numbers like this: (a + bi) + (c + di) = (a + c) + (b + d)i: We multiply complex numbers just like polynomials, but substituting −1 for i2: (a + bi)(c + di) = ac + (ad + bc)i + bd(i2) = (ac − bd) + (ad + bc)i: The order of multiplication doesn't matter since (a + bi)(c + di) = (c + di)(a + bi). a Draw a + bi 2 as the vector 2 2. C b R Theorem (Fundamental theorem of algebra). Suppose n n−1 p(x) = anx + an−1x + : : : a1x + a0 is a polynomial of degree n (meaning an 6= 0) with coefficients a0; a1; : : : ; an 2 C. Then there are n (not necessarily distinct) numbers r1; r2; : : : ; rn 2 C such that n p(x) = (−1) an(r1 − x)(r2 − x) ··· (rn − x): One calls the numbers r1; r2; : : : ; rn the roots of p(x). A root r has multiplicity m if exactly m of the numbers r1; r2; : : : ; rn are equal to r. Define Cn as the set of vectors with n-rows and entries in C, that is: 82 3 9 v1 > > <>6 v2 7 => n = 6 7 : v ; v ; : : : ; v 2 : C 6 : 7 1 2 n C >4 : 5 > > > : vn ; We have Rn ⊂ Cn.
    [Show full text]
  • Chapter 2 Complex Analysis
    Chapter 2 Complex Analysis In this part of the course we will study some basic complex analysis. This is an extremely useful and beautiful part of mathematics and forms the basis of many techniques employed in many branches of mathematics and physics. We will extend the notions of derivatives and integrals, familiar from calculus, to the case of complex functions of a complex variable. In so doing we will come across analytic functions, which form the centerpiece of this part of the course. In fact, to a large extent complex analysis is the study of analytic functions. After a brief review of complex numbers as points in the complex plane, we will ¯rst discuss analyticity and give plenty of examples of analytic functions. We will then discuss complex integration, culminating with the generalised Cauchy Integral Formula, and some of its applications. We then go on to discuss the power series representations of analytic functions and the residue calculus, which will allow us to compute many real integrals and in¯nite sums very easily via complex integration. 2.1 Analytic functions In this section we will study complex functions of a complex variable. We will see that di®erentiability of such a function is a non-trivial property, giving rise to the concept of an analytic function. We will then study many examples of analytic functions. In fact, the construction of analytic functions will form a basic leitmotif for this part of the course. 2.1.1 The complex plane We already discussed complex numbers briefly in Section 1.3.5.
    [Show full text]