Quantum Computation and Hidden Variables.*
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Moscow State University of Technology “STANKIN” PROGRAM
Moscow State University of Technology “STANKIN” PROGRAM V International Conference MODELING OF NON-LINEAR PROCESSES AND SYSTEMS Moscow 2020 SCHEDULE 16.11.20 Opening, Plenary session - 14.00-18.00 17.11.20 Plenary session - 12.00-15.00 18.11.20 Plenary session - 14.00- 14.40 18.11.20 Section 2. PROBLEMS OF ARTIFICIAL INTELLIGENCE – 13.00-18.00 Section 1. MATHEMATICAL MODELING METHODS AND APPLICATIONS – 10.00-13.45, 15.00-20.00 Section 6. WORKSHOP ON ADVANCED MATERIALS PROCESSING AND SMART MANUFACTURING – 10.00- 13.45, 15.00-18.00 19.11.20 Section 5. MODELING IN TECHNICAL SYSTEMS (INCLUDING MANAGEMENT) – 12.00-15.00 Section 3. MODELS OF KINETICS AND BIOPHYSICS- 10.00- 11.50, 14.30- 19.00 20.11.20 Section 4. ECONOMIC AND SOCIAL PROBLEMS – 13.00 – 16.30 - Invitations to participate in the ZOOM conference will be sent by the organizing Committee and the section chairs - Manuscripts can be submitted until December 1, 2020 - Please send your proposals for inclusion in the conference Decision to the organizing Committee by December 1, 2020 Note. There may be minor changes to the conference program Address: 1 and 3a, Vadkovskii lane, MSUT “STANKIN”, “Mendeleevskaya” Metro Station, two stops by any bus to “Vadkovskii pereulok” (towards Savelovskaya Metro Station) Contact: Organizing Committee +7(499) 972-95-20, +7(499)972-94-59 Room 404 or 357a, Department of Applied Mathematics, Vadkovskii lane, 3a +7-916-178-32-11 +7-926-387-91-80 2 PLENARY INTERNET-SESSION Monday, 16.11.2020 Lecture Hall 0311 14. -

As of September 30, 2014
LIST OF AFFILIATES of Sberbank of Russia Open Joint-Stock Company (specify full corporate name of joint-stock company) Issuer code: 0 1 4 8 1 – В as of 0 9 / 3 0 / 2 0 1 4 (specify the date as of which the list of affiliated persons of the joint-stock company is compiled) Location of the issuer: 19 Vavilova St., Moscow, 117997 Russia. (specify the address (address of the permanent executive body of the joint- stock company (or other person authorized to act on behalf of joint-stock company with no power of attorney))) Information contained in this list of affiliates is subject to disclosure pursuant to the laws of the Russian Federation on securities Web page: http://www.sberbank.ru (specify the Web site used by the issuer to disclose information) Deputy Chairman of the Executive Board Sberbank of Russia Bella I. Zlatkis (name, patronymic, (signature) surname) Date 2 October 201 4 . L.S. Issuer’s codes: INN (Taxpayer Identification Number) 7707083893 OGRN (Primary State Registration Number) 1027700132195 I. Composition of affiliated persons as of 0 9 / 3 0 / 2 0 1 4 No. Full corporate name (or name, for Address of legal entity or place of Ground (grounds) for recognizing Date of ground Affiliated person’s Percentage of nonprofit organization) or surname, name residence of individual (to be the person as affiliated (grounds) participatory interest ordinary shares of and patronymic of affiliated person indicated upon authorization of in the share capital of the joint-stock individual only) the joint-stock company owned by company, % the affiliated person, % 1 2 3 4 5 6 7 The entity is entitled to dispose of more than 20 % of the total 12 Neglinnaya St., Moscow, 1 Central Bank of the Russian Federation number of votes attached to 3/21/1991 50.000000004 52.316214 107016 voting shares of Sberbank of Russia OJSC 1. -

Biotechnology in Russia: Why Is It Not a Success Story?
Biotechnology in Russia: Why is it not a success story? Biotechnology inRussia:Whyisitnotasuccessstory? ROGER ROFFEY Biotechnology in Russia: Why is it not a success story? According to President Medvedev 2009 ‘By and large, our industry continues to make the same outdated products and, as a rule, imported generics from substances bought abroad. There is practically no work to create original medicines and technologies.’…‘We must begin the modernisation and technological upgrading of our entire industrial sector. I see this as a question of our country’s survival in the modern world’… ‘These are the key tasks for placing Russia on a new technological level and making it a global leader’. Many states including Russia see biotechnology and its commercialization as a key driver for their future growth. The biotechnology area is characterized by being a very knowledge-intensive activity where there is increasing global competition for know-how. Russia had a very good historical base of R&D and know- how in biotechnology from the previous Soviet military programme. There have been many attempts since 2000 to revive the Russian biotechnology industry not least in 2005 but without much success. In 2009 there were again very ambitious programmes and strategies developed as well as techno-parks for the ROGERROFFEY development of the biotechnology and pharmaceuticals industry up to 2020. It has also been announced by President Medvedev the creation of a Russian equivalent to ‘Silicon Valley’ to include R&D also in biotechnology outside Moscow. There have been many such grand plans but so far they have not been very successful and the question for this study was if it would be different this time? Why are scientists still leaving Russia and foreign investors still hesitating to invest in Russian biotechnology or pharmaceuticals? Why is Russia still not able to compete on the global biotechnology market and is ranked only as number 70 in the world? The current problems and prospects for the biotechnology and pharmaceuticals industries are analysed. -

Code of the Issuer: 0 1 4
LIST OF AFFILIATES of Sberbank of Russia Open Joint-Stock Company (Indicate full company name of the joint-stock company) Code of the 0 1 4 8 1 - В issuer: as of 0 1 0 4 2 0 1 2 (Indicate the date of the list of affiliates of the joint-stock company) Location of the issuer: 19 Vavilova St., Moscow, 117997, Russian Federation (Indicate location (address of the permanent executive body of the joint-stock company (other party entitled to act on behalf of the joint-stock company without the Power of Attorney))) The information contained in this list of affiliates is subject to disclosure in accordance with the laws of the Russian Federation on securities Web page: http://www.sberbank.ru (Indicate the address of the web page used by the issuer to disclose information) Deputy Chairman of the Management Board, OJSC Sberbank of Russia Bella I. Zlatkis (Signature) (Full name) Date: April 03 201 2 Affix Seal Here Codes of the issuer INN (Taxpayer Identification Number): 7707083893 OGRN (Primary State Registration Number): 1027700132195 I. Composition of affiliates as of 0 1 0 4 2 0 1 2 No. Full company name (name of nonprofit Location of the legal entity or place of Grounds for recognizing a person as Date of the Interest of the affiliate Percentage of entity) or full name of the affiliate residence for an individual (Indicate an affiliate grounds in the Charter Capital ordinary shares of the only upon consent of the individual) of the joint-stock joint-stock company company, % owned by the affiliate, % 1 2 3 4 5 6 7 Entity may dispose of more than 12 Neglinnaya St., 107016 Moscow, 20% of the total number of votes 1 Central Bank of Russian Federation March 21, 1991 57.584004 60.251542 Russian Federation attached to the voting shares of Sberbank of Russia 1. -

Refractory High-Entropy Hftatinbzr-Based Alloys by Combined Use of Ball Milling and Spark Plasma Sintering: Effect of Milling Intensity
metals Article Refractory High-Entropy HfTaTiNbZr-Based Alloys by Combined Use of Ball Milling and Spark Plasma Sintering: Effect of Milling Intensity Natalia Shkodich 1,2,*, Alexey Sedegov 1, Kirill Kuskov 1 , Sergey Busurin 3, Yury Scheck 2, Sergey Vadchenko 2 and Dmitry Moskovskikh 1 1 Center of Functional Nanoceramics, National University of Science and Technology MISIS, Moscow 119049, Russia; [email protected] (A.S.); [email protected] (K.K.); [email protected] (D.M.) 2 Merzhanov Institute of Structural Macrokinetics and Materials Science, Russian Academy of Sciences, Chernogolovka, Moscow 142432, Russia; [email protected] (Y.S.); [email protected] (S.V.) 3 NTO IRE-POLUS, LCC, Fryazino, Moscow 141190, Russia; [email protected] * Correspondence: [email protected]; Tel.: +7-49652-46-299 Received: 1 September 2020; Accepted: 18 September 2020; Published: 20 September 2020 Abstract: For the first time, a powder of refractory body-centered cubic (bcc) HfTaTiNbZr-based high-entropy alloy (RHEA) was prepared by short-term (90 min) high-energy ball milling (HEBM) followed by spark plasma sintering (SPS) at 1300 ◦C for 10 min and the resultant bulk material was characterized by XRD and SEM/EDX. The material showed ultra-high Vickers hardness (10.7 GPa) and a density of 9.87 0.18 g/cm3 (98.7%). Our alloy was found to consist of HfZrTiTaNb-based ± solid solution with bcc structure as a main phase, a hexagonal closest packed (hcp) Hf/Zr-based solid solution, and Me2Fe phases (Me = Hf, Zr) as minor admixtures. Principal elements of the HEA phase were uniformly distributed over the bulk of HfTaTiNbZr-based alloy. -
Promarm's Reference-List
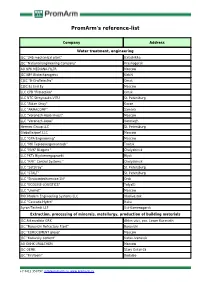
PromArm's reference-list Company Address Water treatment, engineering JSC "345 mechanical plant" Balashikha JSC "National Engineering Company" Krasnogorsk AO NPK MEDIANA-FILTR Moscow JSC NPP Biotechprogress Kirishi CJSC "B-Graffelectro" Omsk CJSC Es End Ey Moscow LLC CPB "Protection" Omsk LLC NTC Stroynauka-VITU St. Petersburg LLC "Aidan Stroy" Kazan LLC "ARMACOMP" Samara LLC "Voronezh-Aqua Invest" Moscow LLC "Voronezh-Aqua" Voronezh Hermes Group LLC St. Petersburg Globaltexport LLC Moscow LLC "GPA Engineering" Moscow LLC "MK Teploenergomontazh" Troitsk LLC "NVK" Niagara " Chelyabinsk LLC PKTs Biyskenergoproekt Biysk LLC "RPK" Control Systems " Chelyabinsk LLC "SetStroy" St. Petersburg LLC "STALT" St. Petersburg LLC "Stroisantechservice-1N" Orsk LLC "ECOLINE-LOGISTICS" Tolyatti LLC "Unimet" Moscow PKK Modern Engineering Systems LLC Vladivostok LLC "Cascade-Hydro" Baku Ayron-Technik LLP Ust-Kamenogorsk Extraction, processing of minerals, metallurgy, production of building materials JSC Aldanzoloto GRK Aldan ulus, pos. Lower Kuranakh JSC "Borovichi Refractory Plant" Borovichi JSC "EUROCEMENT group" Moscow JSC "Katavsky cement" Katav-Ivanovsk AO OKHK URALCHEM Moscow JSC OEMK Stary Oskol-15 JSC "Firstborn" Bodaibo +7 8412 350797, [email protected], www.promarm.ru JSC "Aleksandrovsky Mine" Mogochinsky district of Davenda JSC RUSAL Ural Kamensk-Uralsky JSC "SUAL" Kamensk-Uralsky JSC "Khiagda" Bounty district, with. Bagdarin JSC "RUSAL Sayanogorsk" Sayanogorsk CJSC "Karabashmed" Karabash CJSC "Liskinsky gas silicate" Voronezh CJSC "Mansurovsky career management" Istra district, Alekseevka village Mineralintech CJSC Norilsk JSC "Oskolcement" Stary Oskol CJSC RCI Podolsk Refractories Shcherbinka Bonolit OJSC - Construction Solutions Old Kupavna LLC "AGMK" Amursk LLC "Borgazobeton" Boron Volga Cement LLC Nizhny Novgorod LLC "VOLMA-Absalyamovo" Yutazinsky district, with. Absalyamovo LLC "VOLMA-Orenburg" Belyaevsky district, pos. -

Transport Factor and Types of Settlement Development in the Suburban Area of the Moscow Capital Region
E3S Web of Conferences 210, 09008 (2020) https://doi.org/10.1051/e3sconf/202021009008 ITSE-2020 Transport factor and types of settlement development in the suburban area of the Moscow capital region Petr Krylov1,* 1Moscow Region State University, 105005, Radio str, 10A, Moscow, Russia Abstract. The paper considers the ratio of the transport factor and the types of development of settlements in the suburban area of the Moscow capital region. The purpose of this research is to study the specific features of the development of settlements in various radial directions from the node (core) of Moscow capital region – the Moscow city. Data from publicly available electronic maps were used, including data from the public cadastral map. Historical and socio-economic prerequisites for the formation of various types of development along radial transport axes (public roads of regional and federal significance connecting Moscow with the territory of the Moscow region and other regions of Russia) are considered. Conclusions about the general and specific features of development along different directions at different distances from Moscow are drawn. The research confirms the hypothesis that the ratio of certain types of residential development along various highways differs from place to place depending on the time of the origin of the transport routes themselves, on the economically determined choice of investors, and in recent years – on the environmentally determined choice of the population. 1 Introduction The transport factor is one of the most important for the formation of the settlement system both through the level of transport development of the territory, and taking into account the variety of forms of transport accessibility and connectivity of spatial elements of the territory. -

As of October 1, 2012
LIST OF AFFILIATES of Sberbank of Russia Open Joint-Stock Company (Indicate full company name of the joint-stock company) Issuer code: 0 1 4 8 1 – В as of 1 0 / 0 1 / 2 0 1 2 (Indicate the date of the list of affiliates of the joint- stock company) Location of the issuer: 19 Vavilova St., Moscow 117997, Russia. (Indicate location (address of the permanent executive body of the joint-stock company (other party entitled to act on behalf of the joint-stock company without the Power of Attorney))) The information contained in this list of affiliates is subject to disclosure in accordance with the laws of the Russian Federation on securities Website address: http://www.sberbank.ru (Indicate the address of the web page used by the issuer to disclose information) Deputy Chairman of the Management Board, Sberbank of Russia OJSC No. B. I. Zlatkis (signature) (Full Name) Date: October 3 201 2 L.S. Codes of the issuer TIN 7707083893 PSRN : 1027700132195 I. Composition of affiliates as of 1 0 / 0 1 / 2 0 1 2 No. Full company name (name of nonprofit Location of the legal entity or place Grounds for recognizing the Date of the Interest of the affiliate Percentage of entity) or full name of the affiliate of residence for individual (Indicate person as an affiliate grounds in the Share Capital ordinary shares of only upon consent of the individual) of the joint-stock the joint-stock company, % company owned by the affiliate, % 1 2 3 4 5 6 7 Entity may dispose of more than 12 Neglinnaya St., 107016 20 % of the total number of votes 1 Central Bank of the Russian Federation 3/21/1991 50.000000004 52.316214 Moscow, Russian Federation attached to the voting shares of Sberbank of Russia OJSC 1. -

Preliminary List of Participants (Pdf)
Preliminary list of participants 1 Abgaryan Vahagn JINR, Dubna 2 Alekseev Georgy Steklov Mathematical Institute, Moscow 3 Aminov Gleb ITEP, Moscow 4 Artamonov Semen Moscow Institute of Physics and Technology 5 Belavin Alexander Landau Institute, Chernogolovka 6 Berntson Bjorn Imperial College London, UK 7 Bershtein Mikhail Landau Institute / Independent University of Moscow 8 Bilenky Samoil JINR, Dubna 9 Bogoliubov Nikolai Steklov Mathematical Institute, St. Petersburg 10 Bogolubsky Igor JINR, Dubna 11 Boos Germann University of Wuppertal, Germany 12 Burdik Cestmir CVUT in Prague / JINR, Dubna 13 Bytsko Andrey Steklov Math. Institute, St. Petersburg / Geneva University 14 Chekhov Leonid Steklov Mathematical Institute, Moscow 15 Chicherin Dmitry Steklov Mathematical Institute, St. Petersburg 16 Derkachov Sergey PDMI, St. Petersburg 17 Dimofte Tudor Institute for Advanced Study, Princeton 18 Dobryanskaya Polina JINR, Dubna 19 Donskova Tatyana JINR, Dubna 20 Faddeev Ludwig Steklov Mathematical Institute, St. Petersburg 21 Fedoruk Sergey JINR, Dubna 22 Feigin Evgeny HSE, Moscow 23 Filippov Alexandr JINR, BLTP 24 Fursaev Dmitry DIU / JINR, Dubna 25 Gamayun Alexander Bogolyubov Institute for Theoretical Physics, Kiev 26 Gavrylenko Pavlo Kyiv National University, Ukraine 27 Gladyshev Alexey JINR, Dubna 28 Goehmann Frank Bergische Universitaet Wuppertal, Germany 29 Gorsky Alexander ITEP, Moscow 30 Grishina Olga HSE, Moscow 31 Helminck Gerardus KdV Institute, Amsterdam 32 Hosomichi Kazuo Yukawa Institute for Theoretical Physics, Kyoto 33 Iorgov Nikolai Bogolyubov Institute for Theoretical Physics, Kiev 34 Isaev Alexei JINR, Dubna 35 Ivanov Evgeny JINR, Dubna 36 Kadyshevsky Vladimir JINR, Dubna 37 Kazakov Dmitri JINR, Dubna 38 Kazakov Vladimir de l'Ecole Normale Supérieure et l'Université Paris-VI 39 Khoroshkin Sergey ITEP, Moscow 40 Kim Seok Seoul National University, South Korea 41 Kolganova Elena JINR, Dubna 42 Krivonos Sergey JINR, Dubna 43 Kulish Petr Steklov Mathematical Institute, St. -

As of December 31, 2014
LIST OF AFFILIATES Sberbank of Russia Open Joint-Stock Company (Indicate full corporate name of the joint-stock company) Issuer code: 0 1 4 8 1 – В as of 1 2 / 3 1 / 2 0 1 4 (Indicate the date of the list of affiliates of the joint- stock company) Location of the issuer: 19 Vavilova St., Moscow, 117997 Russia. (Indicate location (address of the permanent executive body of the joint-stock company (other entity entitled to act on behalf of the joint-stock company without the Power of Attorney))) The information contained in this list of affiliates is subject to disclosure in accordance with the laws of the Russian Federation on securities Internet page address: http://www.sberbank.ru; http://www.e-disclosure.ru/portal/company.aspx?id=3043 (Indicate the address of web page used by the issuer to disclose information) Deputy Chairman of the Executive Board, Sberbank of Russia Bella I. Zlatkis (Signature) (Full Name) Date: 13 . January 201 5 . L. S. Issuer codes: INN (Taxpayer Identification Number) 7707083893 OGRN (Primary State Registration Number) 1027700132195 I. Affiliates as of 1 2 / 3 1 / 2 0 1 4 No. Full corporate name (or name, for non- Address of legal entity or place of Ground (grounds) for recognizing Date of ground Interest of the affiliate Percentage of profit entity) or full name of affiliate residence of individual (to be the person as an affiliate (grounds) in the authorized ordinary shares of indicated only upon consent of capital of joint-stock the joint-stock individual) company, % company owned by the affiliate, % 1 2 3 4 5 6 7 Entity may dispose of more than The Central Bank of the Russian 12 Neglinnaya St., Moscow, 20 % of the total number of votes 1 3/21/1991 50.000000004 52.316214 Federation 107016 Russian Federation attached to the voting shares of Sberbank of Russia 1. -

An Evaluation of the Results of the Duma Elections
RUSSIAN ANALYTICAL DIGEST No. 108, 6 February 2012 2 Analysis An evaluation of the Results of the Duma elections By Arkady Lyubarev, Moscow Abstract The Duma elections were first and foremost a contest between the state executive, which made use of all administrative resources, and various societal groups forming the opposition. Ultimately, United Russia was able to win a majority, but the number of protest votes nevertheless increased significantly. Considerable variation in the results could be observed from region to region and even within individual regions. This can partly be attributed to the varying level of falsification in different areas. Overall, by falsifying the result of the vote, it is probable that United Russia was given 15 million extra votes, so that the true result for the party can be seen to stand at around 34% and not 49%. executive Government as an election ted by election day; following election day the number Campaigner of reports rose to 7,800. The main peculiarity of the 2011 election to the State Duma was to be found in the fact that the central contest The election Result did not take place between the seven registered parties. The following table shows the official results of the -par Instead, one of the competing sides was the authorities ties and a comparison with the 2007 Duma elections. at all levels, who threw all their resources into support- According to official figures, United Russia received ing United Russia. just under 50% of the vote and was able to command The candidate list of United Russia was headed by an outright majority of the mandates. -

Scientific Researches
MOSCOW POWER ENGINEERING INSTITUTE (TECHNICAL UNIVERSITY) SCIENTIFIC RESEARCHES 2007—2008 Moscow MPEI Publishing House 2009 INSTITUTE OF POWER MACHINERY AND MECHANICS (IPMM) Institute Ph. D. (Techn.), Professor Sergey A. Serkov Director Ph.: (495) 362-7261 Fax: (495) 362-7428 E-mail: [email protected] Institute Steam Generator Design (SGD) Department ....1.2 Departments Steam and Gas Turbines (SGT) Department ....1.5 Hydrodynamics and Hydraulic Machines (HHM) and Divisions Department 1.8 Bases of Power Engineering Machines Design (BPEMD) Department 1.10 Dynamics and Strength of the Machines Named after V.V. Bolotin (DSM) Department 1.13 Dynamics and Strength of Machinery (DSM) Department 1.16 Metals Technology (MT) Department .......... 1.18 Engineering Drawing (ED) Department ....... 1.21 Research & Development Academic Center of Geothermal Energetic (CGE) 1.22 1.1 IPMM STEAM GENERATOR DESIGN (SGD) DEPARTMENT Ph.: (495) 362-7600, ph/fax: (495) 362-7901, E-mail: [email protected]; [email protected] At SGD Department: 9 teachers, 4 researchers, 3 Ph.D. students. Head of Department Dr. Sci. (Techn.), Professor Pavel V. Roslyakov Main lines of research Research Supervisor Development and implementation of the highly efficient environmentally friendly technologies for organic fuels firing Professor Roslyakov P.V., Head of R&D Lab Molchanov V.A. Reliability and operation effectiveness increase for the steam boilers of TPP Professors Dvoinishnikov V.A., Iziumov M.A., Roslyakov P.V., Head of R&D Lab Molchanov V.A. Development of computer-aided-design technologies for the power ma- chinery equipment Professor Iziumov M.A., Associated-Professor Kniazkov V.P. Mathematical modeling of the nitrogen and sulfur oxides, the polycyclic benzene polycarbons process formation at fuel firing in the power engi- neering equipment Professor Roslyakov P.V.