DOCSLIB.ORG

Exploring the Ii-Vi Chord Progression

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Exploring the Ii-Vi Chord Progression CHAPTER 9: EXPLORING THE II-V-I CHORD PROGRESSION The purpose of this chapter is to explore an important source of tonality in Western music, a musically related sequence of chords called a chord progression. The chapter begins by discussing chord progressions in the context of establishing tonality. It then describes an important chord progression in jazz called the ii-V-I progression. The goal of this chapter is to train a number of different networks on this progression; when provided one chord, the network is trained to respond with the next chord in the progression that should be played. While all of the networks in the chapter are trained on the same jazz progression problem, different networks use different codes to represent input and output chords. The question of interest is whether the choice of encoding has any effect on the ease of discovering a solution to the progression problem. We present results that show that this is definitely true: when an abstract encoding is employed, a multilayer perceptron with many hidden units is required to learn the chord progression. In contrast, when different encodings are used the same problem can be learned by a perceptron that has no hidden units at all. We demonstrate a practical implication of this by demonstrating that a simple network can be easily interpreted. We end the chapter by pointing out that other factors might influence encoding selection; depending on the goals of a simulation, one may not always be seeking the encoding that leads to the simplest network solution. 9.1 Tonality and Chord Progressions ............................... 2 9.2 The ii-V-I Progression .................................................. 5 9.3 The Importance of Encodings ..................................... 8 9.4 Four Encodings of the ii-V-I Problem ....................... 10 9.5 Simulations With Pitch-Class Encoding .................. 15 9.6 Simulations Using Pitch Encodings of Root Forms 17 9.7 Simulations Using Pitch Encodings of Inverted Forms ............................................................................... 18 9.8 Simulations Using Lead Sheet Encodings ............... 19 9.9 Interpreting A Lead Sheet Perceptron ...................... 20 9.10 A Progression of Progressions .............................. 26 9.11 Summary and Implications ..................................... 31 9.12 References ............................................................... 34 © Michael R. W. Dawson 2014 Chapter 9 Exploring the ii-V-I Progression 2 9.1 Tonality and Chord Progressions Tonality is a central characteristic of of balanced support of the tonic, like two Western music (Piston, 1962; Schoenberg, equidistant weights on either side of a 1969). Tonality is the sense that a fulcrum” (Piston, 1962, p. 31). Alternatively, composition belongs to a particular musical some tones are intrinsically unstable in a key, and has been a topic central to many of particular musical key; their presence the earlier parts of this book, including produces a musical tension that demands Chapter 3 on identifying scale tonics, resolution in the form of hearing a more Chapter 4 on identifying scale modes, and stable musical entity. Chapter 5 on key finding. Establishing tonality, then, also requires In what is known as the era of ‘common communicating and exploiting the various practice’ in Western classical music, which relationships amongst tones in a musical spans the 18th and 19th centuries, key. “It is more a process of setting forth the establishing a musical key almost always organized relationship of these tones to one meant establishing a major or minor key of among them which is to be the tonal center” the type that we have already encountered (Piston, 1962, p. 31). In common practice in previous chapters. Although other modes the process of establishing tonality and its can and have been used in Western structure is accomplished by using harmony. compositions, they are essentially ignored by common practice’s focus on the ‘major- The basic element of harmony is the minor system’ of music. “We are so imbued musical interval, the simultaneous presence with this tradition that we tend to interpret of two tones a specific musical distance music based on other modes as being in apart. Chords involve the presentation of either major or minor, usually with somewhat more than two simultaneous tones, and unsatisfactory results” (Piston, 1962, p. 30). therefore the presence of more than one musical interval. Earlier in Chapter 7 we In our earlier chapters on the modality saw how one could construct particular and tonics of musical scales we noted that chords (triads and tetrachords) on each of one could define a musical key by the degrees of a musical scale (Figure 7- constraining pitch-class choice: specifically, 15). Accounts of harmony often begin by by only using tones that belonged to a considering the use of, and the relationship particular scale. For instance, to set a between, triads (Piston, 1962; Schoenberg, composition in the key of C major a 1969). composer would only select its tones from the C major scale, and not employ tones Just as the presence of a single tone that do not belong to this scale. cannot by itself establish a musical key, the occurrence of a triad in isolation cannot However, establishing tonality is more establish tonality. “A triad standing alone is complex than merely restricting the use of entirely indefinite in its harmonic meaning; it particular tones. The tones that define a may be the tonic of one tonality or one musical scale have an organized degree of several others” (Schoenberg, relationship to one another, relationships 1969, p. 1). In order for tonality to be that even listeners with no musical training established, a succession of triads must be are aware of (Krumhansl, 1990). Because presented. The succession must be of these relationships, different tones in a structured so that there is the relationship scale – typically identified by their scale from one triad to the next takes the listener degree (i.e. the Roman numerals used to an intended goal. Such a structured earlier in Figures 4-11 and 7-15), such as I succession of chords is called a chord for the tonic, IV for the subdominant, and V progression. In jazz a chord progression is for the dominant – have specific tonal often called ‘the changes’. functions. There are two strongly related aspects to For example, “dominant and creating a chord progression: establishing a subdominant seem to given an impression sequence of chord roots, and defining the © Michael R. W. Dawson 2014 Chapter 9 Exploring the ii-V-I Progression 3 structure of each chord to establish an imperfect cadence or a half cadence appropriate voice leading. Let us briefly ends on a V chord, and can be preceded by consider these two aspects in turn. any of a number of different chords (e.g. IV or I). The tension produced by ending on Defining a particular succession of the V chord provides a clear signal that chords requires considering the succession further music is coming. It is “like a comma, of chord roots independently of the form (the indicating a partial stop in an unfinished inversion) of each chord. “Chord succession statement” (Piston, 1962, p. 60). can be reduced to root succession (or root progression), which in turn can be translated Root progressions can also be used to into Roman numerals representing a perform other functions, such as modulating succession of scale degrees” (Piston, 1962, from one musical key to another p. 18). Piston notes that common practice (Schoenberg, 1969). We saw earlier in reveals a set of typical root progressions Chapter 4 that different musical scales are which are summarized in Table 9-1. Each similar to one another because they share row of this table provides the root of the many tones. As a result the same chord can current chord in a progression, and notes be found in more than one musical key; the root of the next chord that typically these are called common chords. follows, that sometimes follows, and that less often follows. For instance its first row For instance, A minor is a common chord can be interpreted as “If the current chord found in both the key of C major (where it is has I as its root, it is typically followed by a the built on the VI scale degree) and in the IV or by a V chord, it is sometimes followed key of G major (where it is built on the II by a VI chord, and it is less often followed by scale degree). One can therefore use A a II or III chord.” minor as a pivot chord in a cadence that modulates the key of a composition from C Less Root Of Typically Sometimes major to G major. Often Current Followed Followed Followed Chord By By By Root successions are only aspect of a I IV or V VI II or III chord progression. A second strongly II V VI I, III, or IV related aspect is voice leading (see the III VI IV II or V earlier discussion of this term in Section IV V I or II III or VI 4.5.3). In choral music different voices V I VI or IV III or II perform the component notes of each chord VI II or V III or IV I VII III in a progression. In addition to defining the Table 9-1. The usual progression of chord roots in succession of chord roots in this common practice. See text for details. progression, a composer of choral music must also decide which voice is to move Why do the root progressions from one tone in the first chord to another summarized in Table 9-1 emerge from tone in the second. common practice? The reason is that the relations amongst chords with these roots in Common practice adopts principles that terms of a particular tonal center are such lead to efficient voice leading, which that they instill a particular musical direction attempts to minimize the musical distance to a listener.
Load more

Recommended publications
  • The Care and Feeding of the WHOLE MUSICAL YOU! Created by the Students and Instructors of the New Trier Jazz Ensembles Program
    The Care and Feeding of the WHOLE MUSICAL YOU! Created by the students and instructors of the New Trier Jazz Ensembles Program The many domains of the whole musical you… TECHNICIAN LITERATE JAZZ MUSICIAN COMPOSER/ARRANGER IMPROVISER LISTENER CRITIC HISTORIAN PERFORMER Tools/resources needed to develop the whole musical you… desire goals time space guidance enjoyment DEVELOPING AS A TECHNICIAN Practice with a metronome Track your progress – make your assessment quantitative (numbers) Take small, measured steps Record yourself, and be critical (also be positive) Use SmartMusic as a scale-practicing companion Go bonkers with scales Be creative with scales (play scales in intervals, play scales through the entire range of your instrument, play scales starting on notes other than the tonic, remember that every scale also represents a chord for each note in that scale, find new patterns in your scales Challenge yourself – push your boundaries Use etudes and solo transcriptions to push yourself Use a metronome!!! DEVELOPING AS A LITERATE JAZZ MUSICIAN Practice sight-reading during every session Learn tunes (from the definitive recorded version when possible) Learn vocabulary Learn chords on the piano DEVELOPING AS A COMPOSER/ARRANGER Compose a melody Compose a chord progression Compose a melody on an established chord progression (called a contrafact) Re-harmonize an established melody Write an arrangement of an established melody DEVELOPING AS AN IMPROVISER Transcribe a solo Compose a solo for a tune you’re
    [Show full text]
  • Harmony Crib Sheets
    Jazz Harmony Primer General stuff There are two main types of harmony found in modern Western music: 1) Modal 2) Functional Modal harmony generally involves a static drone, riff or chord over which you have melodies with notes chosen from various scales. It’s common in rock, modern jazz and electronic dance music. It predates functional harmony, too. In some types of modal music – for example in jazz - you get different modes/chord scale sounds over the course of a piece. Chords and melodies can be drawn from these scales. This kind of harmony is suited to the guitar due to its open strings and retuning possibilities. We see the guitar take over as a songwriting instrument at about the same time as the modes become popular in pop music. Loop based music also encourages this kind of harmony. It has become very common in all areas of music since the late 20th century under the influence of rock and folk music, composers like Steve Reich, modal jazz pioneered by Miles Davis and John Coltrane, and influences from India, the Middle East and pre-classical Western music. Functional harmony is a development of the kind of harmony used by Bach and Mozart. Jazz up to around 1960 was primarily based on this kind of harmony, and jazz improvisation was concerned with the improvising over songs written by the classically trained songwriters and film composers of the era. These composers all played the piano, so in a sense functional harmony is piano harmony. It’s not really guitar shaped. When I talk about functional harmony I’ll mostly be talking about ways we can improvise and compose on pre-existing jazz standards rather than making up new progressions.
    [Show full text]
  • Chapter 12 Answer Key.Indd
    Chapter 12 Answer Key Applications Exercises 1. Spell and resolve dominant seventh chords in root position. Chord voic- ings should be either complete (C) or incomplete (IN), as indicated below the Roman numerals. © 2019 Taylor & Francis 2 Chapter 12 Answer Key 2. Spell and resolve inverted dominant seventh chords. All chords should be complete. Add any necessary inversion symbol to the tonic chord. 3. Spell and resolve leading-tone seventh chords in root position and inversion. Add any necessary inversion symbol to the tonic chord. © 2019 Taylor & Francis Chapter 12 Answer Key 3 4. Complete the following chord progression in four voices. Provide a syntactic analysis below the Roman numerals. The syntactic analysis is shown below the Roman numerals. The voicing of chords and voice leading between chords is variable. Brain Teaser What triad is shared by V7 and viiØ7? How do these two seventh chords differ in terms of their scale-degree contents? Answer: V7 and viiØ7 share the leading-tone triad (viiO). The two chords differ by 5ˆ (the root of V7) and 6ˆ (the seventh of viiØ7). 5ˆ and 6ˆ are a whole step apart (a half step in minor, where 6ˆ is the seventh of viiO7). Thinking Critically An incomplete triad or seventh chord is missing its fifth. Compared with other chord members (root, third, and seventh), why is it possible to omit the fifth (i.e., why is this particular chord member nonessential)? Discussion The root of a chord is necessary to identify the chord and its function, the third determines the quality of the chord (major or minor), and the seventh must be present for a chord to be an actual seventh chord (rather than a triad).
    [Show full text]
  • Many of Us Are Familiar with Popular Major Chord Progressions Like I–IV–V–I
    Many of us are familiar with popular major chord progressions like I–IV–V–I. Now it’s time to delve into the exciting world of minor chords. Minor scales give flavor and emotion to a song, adding a level of musical depth that can make a mediocre song moving and distinct from others. Because so many of our favorite songs are in major keys, those that are in minor keys1 can stand out, and some musical styles like rock or ​ ​ jazz thrive on complex minor scales and harmonic wizardry. Minor chord progressions generally contain richer harmonic possibilities than the typical major progressions. Minor key songs frequently modulate to major and back to minor. Sometimes the same chord can appear as major and minor in the very same song! But this heady harmonic mix is nothing to be afraid of. By the end of this article, you’ll not only understand how minor chords are made, but you’ll know some common minor chord progressions, how to write them, and how to use them in your own music. With enough listening practice, you’ll be able to recognize minor chord progressions in songs almost instantly! Table of Contents: 1. A Tale of Two Tonalities 2. Major or Minor? 3. Chords in Minor Scales 4. The Top 3 Chords in Minor Progressions 5. Exercises in Minor 6. Writing Your Own Minor Chord Progressions 7. Your Minor Journey 1 https://www.musical-u.com/learn/the-ultimate-guide-to-minor-keys A Tale of Two Tonalities Western music is dominated by two tonalities: major and minor.
    [Show full text]
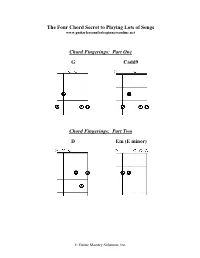
  • Part One G Cadd9 Chord Fingerings
    The Four Chord Secret to Playing Lots of Songs www.guitarlessonsforbeginnersonline.net Chord Fingerings: Part One G Cadd9 Chord Fingerings: Part Two D Em (E minor) © Guitar Mastery Solutions, Inc. Playing Chord Progressions A chord progression is a series of chords played one after the other. Most songs consist of several different chord progressions. Learning to play the chord progressions in this lesson will help you learn to play many different songs. Mastering the chord fingerings and chord progressions in this lesson will help you quickly learn to play many different songs in different styles of music. These fundamental chords are crucial to your development and improvement as a guitar player—learn them well and learn to change between them. You will use them for the rest of your guitar playing career! Chord Progression One Chords Used: D Cadd9 G Play four strums on each chord and change to the next: |D / / / |Cadd9 / / / |G / / / | (repeat) This chord progression is similar to the one used in the song “Can’t You See?” by the Marshall Tucker Band. Chord Progression Two Chords Used: D Cadd9 G This progression uses the same chords as the first one. The difference is that we will pick some of the notes in the first two chords and end with a strum on the final G chord. Key point to remember: Even though the pick hand is playing some single notes, your fret hand only needs to play the chord shapes, just like in Progression One. D Cadd9 G This chord progression and picking pattern is similar to the one used in the song “Sweet Home Alabama” by Lynyrd Skynyrd.
    [Show full text]
  • Seventh Chord Progressions in Major Keys
    Seventh Chord Progressions In Major Keys In this lesson I am going to focus on all of the 7th chord types that are found in Major Keys. I am assuming that you have already gone through the previous lessons on creating chord progressions with basic triads in Major and Minor keys so I won't be going into all of the theory behind it like I did in those lessons. If you haven't read through those lessons AND you don't already have that knowledge under your belt, I suggest you download the FREE lesson PDF on Creating and Writing Major Key Chord Progressions at www.GuitarLessons365.com. So What Makes A Seventh Chord Different From A Triad? A Seventh Chord IS basically a triad with one more note added. If you remember how we can get the notes of a Major Triad by just figuring out the 1st, 3rd and 5th tones of a major scale then understanding that a Major Seventh Chord is a four note chord shouldn't be to hard to grasp. All we need to do is continue the process of skipping thirds to get our chord tones. So a Seventh Chord would be spelled 1st, 3rd, 5th and 7th. The added 7th scale degree is what gives it it's name. That is all it is. :) So what I have done for this theory lesson is just continue what we did with the basic triads, but this time made everything a Seventh Chord. This should just be a simple process of just memorizing each chord type to it's respective scale degree.
    [Show full text]
  • Computational Invention of Cadences and Chord Progressions by Conceptual Chord-Blending
    Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI 2015) Computational Invention of Cadences and Chord Progressions by Conceptual Chord-Blending Manfred Eppe16, Roberto Confalonieri1, Ewen Maclean2, Maximos Kaliakatsos3, Emilios Cambouropoulos3, Marco Schorlemmer1, Mihai Codescu4, Kai-Uwe Kuhnberger¨ 5 1IIIA-CSIC, Barcelona, Spain 2University of Edinburgh, UK 3University of Thessaloniki, Greece fmeppe,confalonieri,[email protected] [email protected] femilios,[email protected] 4University of Magdeburg, Germany 5 University of Osnabruck,¨ Germany 6 ICSI, Berkeley, USA [email protected] [email protected] [email protected] Abstract chord and moves to the tonic, and the seventh resolves down- wards by stepwise motion, whereas the fifth may be omitted. We present a computational framework for chord inven- In the Phrygian cadence, the bass note (third of the chord) is tion based on a cognitive-theoretic perspective on con- ceptual blending. The framework builds on algebraic the most important note as it plays the role of a downward specifications, and solves two musicological problems. leading note, and the second most important note is the root. It automatically finds transitions between chord progres- In such a setup, we propose two applications of chord blend- sions of different keys or idioms, and it substitutes chords ing, to give rise to new cadences and chord progressions. in a chord progression by other chords of a similar func- The first application is to generate a novel cadence as a ‘fu- tion, as a means to create novel variations. The approach sion’ of existing cadences by blending chords with a similar is demonstrated with several examples where jazz ca- function.
    [Show full text]
  • Transfer Theory Placement Exam Guide (Pdf)
    2016-17 GRADUATE/ transfer THEORY PLACEMENT EXAM guide! Texas woman’s university ! ! 1 2016-17 GRADUATE/transferTHEORY PLACEMENTEXAMguide This! guide is meant to help graduate and transfer students prepare for the Graduate/ Transfer Theory Placement Exam. This evaluation is meant to ensure that students have competence in basic tonal harmony. There are two parts to the exam: written and aural. Part One: Written Part Two: Aural ‣ Four voice part-writing to a ‣ Melodic dictation of a given figured bass diatonic melody ‣ Harmonic analysis using ‣ Harmonic Dictation of a Roman numerals diatonic progression, ‣ Transpose a notated notating the soprano, bass, passage to a new key and Roman numerals ‣ Harmonization of a simple ‣ Sightsinging of a melody diatonic melody that contains some functional chromaticism ! Students must achieve a 75% on both the aural and written components of the exam. If a passing score is not received on one or both sections of the exam, the student may be !required to take remedial coursework. Recommended review materials include most of the commonly used undergraduate music theory texts such as: Tonal Harmony by Koska, Payne, and Almén, The Musician’s Guide to Theory and Analysis by Clendinning and Marvin, and Harmony in Context by Francoli. The exam is given prior to the beginning of both the Fall and Spring Semesters. Please check the TWU MUSIc website (www.twu.edu/music) ! for the exact date and time. ! For further information, contact: Dr. Paul Thomas Assistant Professor of Music Theory and Composition [email protected] 2 2016-17 ! ! ! ! table of Contents ! ! ! ! ! 04 Part-Writing ! ! ! ! ! 08 melody harmonization ! ! ! ! ! 13 transposition ! ! ! ! ! 17 Analysis ! ! ! ! ! 21 melodic dictation ! ! ! ! ! harmonic dictation ! 24 ! ! ! ! Sightsinging examples ! 28 ! ! ! 31 terms ! ! ! ! ! 32 online resources ! 3 PART-Writing Part-writing !Realize the following figured bass in four voices.
    [Show full text]
  • Ii-V-I Lesson
    What's Up With II-V-I's 1 An Introduction to the Jazz Language Randy Hunter THE JAZZ VOCABULARY Learning to improvise is often compared with learning to speak a language. As jazz musicians, our objective is to learn to speak through our instruments with the fluency of a great story-teller, using an unresticted vocabulary to enhance our musical narrative with emotion, energy, and creativity. When learning a language, we begin with basic words and word combinations that allow us to express simple ideas. As our vocabulary and understanding of sentence structure grows, we learn to communicate more complex ideas. A similar process can be applied when learning the jazz language. FIRST THINGS FIRST: Developing an understanding of the most basic chords/scales used in jazz and the way these chords work together is critical in learning to speak the jazz language. Minor seventh (m7), dominant seventh (7), . and major seventh (maj7) chords are fundamental to this approach because, in their unaltered forms, they are constructed from modes of major scales. These chords are often grouped together in a common progression known as a II-V-I. In this type of progression, the II and V chords and scales are constructed based on the corresponding second and fifth steps of the major (I) scale. The example below shows a II-V-I progression in the key of C major. Notice in the example that the Dm7 and G7 scales/chords are generated from tones found in the C major scale. These scales are known as the dorian (second) and mixolydian (fifth) modes.
    [Show full text]
  • Chord Progression 1 Chord Progression
    Chord progression 1 Chord progression A chord progression (or harmonic progression) is a series of musical chords, or chord changes that "aims for a definite goal" of establishing (or contradicting) a tonality founded on a key, root or tonic chord.[1] In other words, the succession of root relationships.[2] Chords and chord theory are generally known as harmony. A chord progression can be thought of as a harmonic IV-V-I progression in C Play simultaneity succession: it offers an ongoing shift of level that is essential to the music of Europe (at least since 1600), Oceania and South/West Africa. A change of chord, or "chord change", generally occurs on an accented beat, so that chord progressions may contribute significantly to the rhythm, meter and musical form of a piece, delineating bars, phrases and sections.[3] Basics A chord may be built upon any note of a musical scale, therefore a seven-note scale allows seven basic chords, each degree of the scale becoming the "root" of its own chord.[4] A chord built upon the note A is an A chord of some type, major/minor/diminished/etc. The harmonic function of any particular The key note or tonic of a piece of music is called note number one, the first step of the chord depends on the context of the ascending scale. Chords built on each scale degree are numbered in the same way so that, for example, in the key of C, the progression E minor - F - G can be generally described particular chord progression in which it as a three - four - five progression.
    [Show full text]
  • Arxiv:2001.02360V3 [Cs.SD] 27 Apr 2021
    Automatic Melody Harmonization with Triad Chords: A Comparative Study Yin-Cheng Yeh, Wen-Yi Hsiao, Satoru Fukayama, Tetsuro Kitahara, Benjamin Genchel, Hao-Min Liu, Hao-Wen Dong, Yian Chen, Terence Leong, and Yi-Hsuan Yang ARTICLE HISTORY Compiled April 28, 2021 ABSTRACT Several prior works have proposed various methods for the task of automatic melody harmonization, in which a model aims to generate a sequence of chords to serve as the harmonic accompaniment of a given multiple-bar melody sequence. In this paper, we present a comparative study evaluating and comparing the performance of a set of canonical approaches to this task, including a template matching based model, a hidden Markov based model, a genetic algorithm based model, and two deep learning based models. The evaluation is conducted on a dataset of 9,226 melody/chord pairs we newly collect for this study, considering up to 48 triad chords, using a standardized training/test split. We report the result of an objective evaluation using six different metrics and a subjective study with 202 participants. KEYWORDS Symbolic music generation; automatic melody harmonization; functional harmony 1. Introduction Automatic melody harmonization, a sub-task of automatic music generation (Fern´andez& Vico, 2013), refers to the task of creating computational models that can generate a harmonic accompaniment for a given melody (Chuan & Chew, 2007; Simon, Morris, & Basu, 2008). Here, the term harmony, or harmonization, is used to refer to chordal accompaniment, where an accompaniment is defined relative to the melody as the supporting section of the music. Figure 1 illustrates the inputs and outputs for a melody harmonization model.
    [Show full text]
  • Reharmonizing Chord Progressions
    Reharmonizing Chord Progressions We’re going to spend a little bit of time talking about just a few of the techniques which you’ve already learned about, and how you can use these tools to add interest and movement into your own chord progressions. CHORD INVERSIONS If a song that you’re playing stays on the same chord for several beats, it can begin to sound stagnant if you play the same chord voicing over and over. One of the things you can do to add movement into the chord progression is to stay on the same chord but choose a different inversion of that chord. For instance, if you have 2 consecutive measures where the 1(Major) chord forms the harmony, try playing the first measure using 1 in root position and start the next measure by changing to a 1 over 3 (in other words, use a first inversion 1 chord). In modern chord notation, we’d write this as C/E. Or, if you don’t want to change the bass note– you can at least try using a different ‘voicing’ of the chord: instead of (from bottom to top note) C, G, E, C you might try C, C, G, E or C, G, E, G. For a guitarist, this may mean just playing the chord in a different position. For a keyboardist, you may have to consider which note names are doubled and whether the spacing between notes is closer or farther apart. SUBSTITUTE CHORDS OF SIMILAR QUALITY One of the things we’ve talked about previously is that certain chords in any given key sound ‘at rest’ and certain chords sound with a great deal of tension and feel like they ‘need to resolve’ to a place of rest.
    [Show full text]