1988Apj. . .331. .5833 the Astrophysical Journal, 331:583-604
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dark Matter Thermonuclear Supernova Ignition
MNRAS 000,1{21 (2019) Preprint 1 January 2020 Compiled using MNRAS LATEX style file v3.0 Dark Matter Thermonuclear Supernova Ignition Heinrich Steigerwald,1? Stefano Profumo,2 Davi Rodrigues,1 Valerio Marra1 1Center for Astrophysics and Cosmology (Cosmo-ufes) & Department of Physics, Federal University of Esp´ırito Santo, Vit´oria, ES, Brazil 2Department of Physics and Santa Cruz Institute for Particle Physics, 1156 High St, University of California, Santa Cruz, CA 95064, USA Accepted XXX. Received YYY; in original form ZZZ ABSTRACT We investigate local environmental effects from dark matter (DM) on thermonuclear supernovae (SNe Ia) using publicly available archival data of 224 low-redshift events, in an attempt to shed light on the SN Ia progenitor systems. SNe Ia are explosions of carbon-oxygen (CO) white dwarfs (WDs) that have recently been shown to explode at sub-Chandrasekhar masses; the ignition mechanism remains, however, unknown. Recently, it has been shown that both weakly interacting massive particles (WIMPs) and macroscopic DM candidates such as primordial black holes (PBHs) are capable of triggering the ignition. Here, we present a method to estimate the DM density and velocity dispersion in the vicinity of SN Ia events and nearby WDs; we argue that (i) WIMP ignition is highly unlikely, and that (ii) DM in the form of PBHs distributed according to a (quasi-) log-normal mass distribution with peak log10¹m0/1gº = 24:9±0:9 and width σ = 3:3 ± 1:0 is consistent with SN Ia data, the nearby population of WDs and roughly consistent with other constraints from the literature. -

Abstract Neutral Gas Outflows and Inflows in Local AGN & High-Z Lyman-Α Emitters in COSMOS Hannah Bowen Krug, Doctor Of
Abstract Title of dissertation: Neutral Gas Outflows and Inflows in Local AGN & High-z Lyman-α Emitters in COSMOS Hannah Bowen Krug, Doctor of Philosophy, 2013 Dissertation directed by: Professor Sylvain Veilleux Department of Astronomy This thesis is composed of two parts: (1) a search for neutral gas outflows and inflows in local active galactic nuclei (AGN) and ultraluminous infrared galax- ies (ULIRGs), and (2) a deep and wide imaging search for high-redshift Lyman-α emitters (LAEs). In the first part, we utilize the R-C spectrograph on the Mayall 4m telescope at Kitt Peak National Observatory (KPNO) to look for Na I D ab- sorption. Galactic outflows are thought to play a major role in galactic feedback and evolution, and previous studies of neutral gas have shown that galactic winds occur in most galaxies with high infrared (IR) luminosities. However, in composite systems where a starburst coexists with an active galactic nucleus (AGN), it is un- clear whether the starburst or the AGN is driving the outflows. This thesis attempts to answer that question by looking at samples of Seyfert galaxies, Palomar-Green quasistellar objects (PG QSOs), and ULIRGs. We first describe the results from a search for Na I D outflows in 35 IR- faint Seyferts. We find that the outflow detection rates for IR-faint Seyferts are substantially lower than those of IR-luminous Seyferts. The outflow kinematics of Seyfert 2s resemble those of starburst galaxies, while the outflow velocities in Seyfert 1s are significantly larger. Taken together, these results suggest that the AGN does not play a significant role in driving the outflows in most Seyferts, except the high- velocity outflows seen in Seyfert 1s. -

An Atlas of Calcium Triplet Spectra of Active Galaxies 3
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 1 December 2018 (MN LATEX style file v2.2) An atlas of Calcium triplet spectra of active galaxies A. Garcia-Rissmann1⋆, L. R. Vega1,2†, N. V. Asari1‡, R. Cid Fernandes1§, H. Schmitt3,4¶, R. M. Gonz´alez Delgado5k, T. Storchi-Bergmann6⋆⋆ 1 Depto. de F´ısica - CFM - Universidade Federal de Santa Catarina, C.P. 476, 88040-900, Florian´opolis, SC, Brazil 2 Observatorio Astron´omico de C´ordoba, Laprida 854, 5000, C´ordoba, Argentina 3 Remote Sensing Division, Code 7210, Naval Research Laboratory, 4555 Overlook Avenue, SW, Washington, DC 20375 4 Interferometric Inc., 14120 Parke Long Court, 103, Chantilly, VA20151 5 Instituto de Astrof´ısica de Andaluc´ıa (CSIC), P.O. Box 3004, 18080 Granada, Spain 6 Instituto de F´ısica, Universidade Federal do Rio Grande do Sul, C.P. 15001, 91501-970, Porto Alegre, RS, Brazil 1 December 2018 ABSTRACT We present a spectroscopic atlas of active galactic nuclei covering the region around the λλ8498, 8542, 8662 Calcium triplet (CaT). The sample comprises 78 ob- jects, divided into 43 Seyfert 2s, 26 Seyfert 1s, 3 Starburst and 6 normal galaxies. The spectra pertain to the inner ∼ 300 pc in radius, and thus sample the central kine- matics and stellar populations of active galaxies. The data are used to measure stellar velocity dispersions (σ⋆) both with cross-correlation and direct fitting methods. These measurements are found to be in good agreement with each-other and with those in previous studies for objects in common. The CaT equivalent width is also measured. -

Cfa4: Light Curves for 94 Type Ia Supernovae
CfA4: Light Curves for 94 Type Ia Supernovae Malcolm Hicken1, Peter Challis1, Robert P. Kirshner1, Armin Rest2, Claire E. Cramer3, W. Michael Wood-Vasey4, Gaspar Bakos1,5, Perry Berlind1, Warren R. Brown1, Nelson Caldwell1, Mike Calkins1, Thayne Currie6, Kathy de Kleer7, Gil Esquerdo8, Mark Everett8, Emilio Falco1, Jose Fernandez1, Andrew S. Friedman1, Ted Groner1, Joel Hartman1,5, Matthew J. Holman1, Robert Hutchins1, Sonia Keys1, David Kipping1, Dave Latham1, George H. Marion1, Gautham Narayan1, Michael Pahre1, Andras Pal1, Wayne Peters1, Gopakumar Perumpilly9, Ben Ripman1, Brigitta Sipocz1, Andrew Szentgyorgyi1, Sumin Tang1, Manuel A. P. Torres1, Amali Vaz10, Scott Wolk1, Andreas Zezas1 ABSTRACT We present multi-band optical photometry of 94 spectroscopically-confirmed Type Ia supernovae (SN Ia) in the redshift range 0.0055 to 0.073, obtained be- tween 2006 and 2011. There are a total of 5522 light curve points. We show that our natural system SN photometry has a precision of . 0.03 mag in BVr’i’, . 0.06 mag in u′, and . 0.07 mag in U for points brighter than 17.5 mag and estimate that it has a systematic uncertainty of 0.014, 0.010, 0.012, 0.014, 0.046, and 0.073 mag in BVr’i’u’U, respectively. Comparisons of our standard system photometry with published SN Ia light curves and comparison stars reveal mean agreement across samples in the range of ∼0.00-0.03 mag. We discuss the recent mea- surements of our telescope-plus-detector throughput by direct monochromatic illumination by Cramer et al. (in prep.). This technique measures the -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Repositorio Universidad Nacional
UNIVERSIDAD NACIONAL DE COLOMBIA FACULTAD DE CIENCIAS DEPARTAMENTO DE F´ISICA LA REGION´ DE L´INEAS CORONALES EN GALAXIAS SEYFERT 1 Y SEYFERT 2 Jos´eGregorio Portilla B. Tesis realizada bajo la orientaci´on y direcci´on de los investigadores Dr. Juan Manuel Tejeiro S. (Universidad Nacional de Colombia) y el Dr. Alberto Rodr´ıguez Ardila (Director Asociado) del Laborat´orio Nacional de Astrofisica, M. G., Brasil, y presentada como requisito parcial para la obtenci´on del t´ıtulo de Doctor en f´ısica te´orica. Bogot´a, 2011 . A mis padres Mar´ıa Teresa y Jos´e Gregorio y mi hermano Luis Rodrigo Agradecimientos Reservo este espacio para agradecer a todas aquellas personas que de una u otra forma, con su amistad, apoyo, aliento y conocimientos permitieron que esta tesis llegara a su feliz t´ermino. Mi agradecimiento puntual va para: Alberto Rodr´ıguez-Ardila, a quien le debo mi conocimiento en galaxias activas, por su muy valiosa amistad, su paciencia sin l´ımites, aliento y consejos en los momentos dif´ıciles y por su comprensi´on. Si esta tesis sali´ofinalmente adelante se debe a ´el. Juan Manuel Tejeiro, quien me alent´oa proseguir mis estudios en f´ısica y obtener el doctorado, por su amistad, apoyo incondicional y confianza. Los colegas del Observatorio Astron´omico, por su invaluable amistad, apoyo, comprensi´on y sobre todo aliento. Debo agradecer, muy espec´ıficamente, a Armando Higuera, quien me anim´oa realizar el doctorado conjuntamente con ´el. Su apoyo irrestricto en todo momento permiti´oadentrarme conjuntamente con ´el en el estudio de las galaxias activas. -

THE LOCAL HOSTS of TYPE Ia SUPERNOVAE
The Astrophysical Journal, 707:1449–1465, 2009 December 20 doi:10.1088/0004-637X/707/2/1449 C 2009. The American Astronomical Society. All rights reserved. Printed in the U.S.A. THE LOCAL HOSTS OF TYPE Ia SUPERNOVAE James D. Neill1, Mark Sullivan2, D. Andrew Howell3,4, Alex Conley5,6, Mark Seibert7, D. Christopher Martin1, Tom A. Barlow1, Karl Foster1, Peter G. Friedman1, Patrick Morrissey1, Susan G. Neff8, David Schiminovich9, Ted K. Wyder1, Luciana Bianchi10,Jose´ Donas11, Timothy M. Heckman12, Young-Wook Lee13, Barry F. Madore7, Bruno Milliard11, R. Michael Rich14, and Alex S. Szalay12 1 California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA 2 University of Oxford, Denys Wilkinson Building, Keble Road, Oxford, OX1 3RH, UK 3 Las Cumbres Observatory Global Telescope Network, 6740 Cortona Dr., Suite 102, Goleta, CA 93117, USA 4 Department of Physics, University of California, Santa Barbara, Broida Hall, Mail Code 9530, Santa Barbara, CA 93106-9530, USA 5 Department of Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, ONM5S3H8, Canada 6 Center for Astrophysics and Space Astronomy, University of Colorado, Boulder, CO 80309-0389, USA 7 The Observatories of the Carnegie Institute of Washington, 813 Santa Barbara Street, Pasadena, CA, 91101, USA 8 Laboratory for Astronomy and Solar Physics, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA 9 Department of Astronomy, Columbia University, New York, NY 10027, USA 10 Center for Astrophysical Sciences, Johns Hopkins University, -

19 90Apjs. . .72. .231M the Astrophysical Journal Supplement Series, 72:231-244,1990 February © 1990. the American Astronomical
The Astrophysical Journal Supplement Series, 72:231-244,1990 February .231M © 1990. The American Astronomical Society. All rights reserved. Printed in U.S.A. .72. 90ApJS. SEYFERT GALAXIES. I. MORPHOLOGIES, MAGNITUDES, AND DISKS 19 John W. MacKenty Institute for Astronomy, University of Hawaii, and Space Telescope Science Institute Received 1987 March 18; accepted 1989 July 31 ABSTRACT CCD images of a volume- and luminosity-limited sample of 51 Markarian and NGC Seyfert galaxies show that Seyfert galaxies nearly always possess mechanisms for transporting material into their nuclei (e.g., peculiar, tidally interacting, or barred galaxies). A subset of Seyfert galaxies with amorphous morphologies, some of which may be remnants of past interactions, constitutes approximately one-fifth of the sample. The colors and exponential disk parameters of Seyfert galaxies are generally similar to those of spiral galaxies without active nuclei. Images of the galaxies are presented along with aperture magnitudes. Subject headings: galaxies: nuclei — galaxies: photometry — galaxies: Seyfert — galaxies: structure I. INTRODUCTION one-third of a sample of 58 Seyfert and “Seyfert-like” galaxies have “strong anomahes” in their H I spectra. A larger survey This paper examines the morphologies and colors of Seyfert of 91 Seyferts by Mirabel and Wilson (1984) shows 40% with galaxies. The primary motivation is to extend the efforts of pecuharities attributed to either close companions in the earlier authors through the use of the charge-coupled device telescope beam or tidal interactions that have perturbed the (CCD) detector and by compiling an improved sample of neutral gas in the galaxies. Seyfert galaxies. Somewhat surprisingly, much of the progress in recent In a classic study of the morphology of Seyfert galaxies, years toward an understanding of the host galaxies of AGNs Adams (1977) found that nearly all Seyferts have spiral or comes from studies of low-redshift QSOs. -

Activity of the Seyfert Galaxy Neighbours⋆⋆⋆
A&A 552, A135 (2013) Astronomy DOI: 10.1051/0004-6361/201219606 & c ESO 2013 Astrophysics Activity of the Seyfert galaxy neighbours, E. Koulouridis1,M.Plionis2,3, V. Chavushyan3, D. Dultzin4, Y. Krongold4, I. Georgantopoulos1 , and J. León-Tavares5,6 1 Institute of Astronomy & Astrophysics, National Observatory of Athens, Palaia Penteli 152 36, Athens, Greece e-mail: [email protected] 2 Physics Department of Aristotle, University of Thessaloniki, University Campus, 54124 Thessaloniki, Greece 3 Instituto Nacional de Astrofísica Optica y Electrónica, Puebla, C.P. 72840 México, Mexico 4 Instituto de Astronomía, Universidad Nacional Autónoma de México, Apartado Postal 70-264, D. F. 04510 México, Mexico 5 Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland 6 Aalto University, Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland Received 15 May 2012 / Accepted 23 January 2013 ABSTRACT We present a follow-up study of a series of papers concerning the role of close interactions as a possible triggering mechanism of AGN activity. We have already studied the close (≤100 h−1 kpc) and the large-scale (≤1 h−1 Mpc) environment of a local sample of Sy1, Sy2, and bright IRAS galaxies (BIRG) and of their respective control samples. The results led us to the conclusion that a close encounter appears capable of activating a sequence where an absorption line galaxy (ALG) galaxy first becomes a starburst, then a Sy2, and finally a Sy1. Here we investigate the activity of neighbouring galaxies of different types of AGN, since both galaxies of an interacting pair should be affected. -

Local and Large-Scale Environment of Seyfert Galaxies E
The Astrophysical Journal, 639:37–45, 2006 March 1 A # 2006. The American Astronomical Society. All rights reserved. Printed in U.S.A. LOCAL AND LARGE-SCALE ENVIRONMENT OF SEYFERT GALAXIES E. Koulouridis,1,2 M. Plionis,1,3 V. Chavushyan,3,4 D. Dultzin-Hacyan,4 Y. Krongold,4 and C. Goudis1,2 Received 2005 May 11; accepted 2005 September 28 ABSTRACT We present a three-dimensional study of the local (100 hÀ1 kpc) and the large-scale (1 hÀ1 Mpc) environment of the two main types of Seyfert AGN galaxies. For this purpose we use 48 Seyfert 1 galaxies (with redshifts in the range 0:007 z 0:036) and 56 Seyfert 2 galaxies (with 0:004 z 0:020), located at high galactic latitudes, as well as two control samples of nonactive galaxies having the same morphological, redshift, and diameter size distributions as the corresponding Seyfert samples. Using the Center for Astrophysics (CfA2) and Southern Sky Redshift Survey (SSRS) galaxy catalogs (mB 15:5) and our own spectroscopic observations (mB 18:5), we find that within a projected distance of 100 hÀ1 kpc and a radial velocity separation of v P 600 km sÀ1 around each of our AGNs, the fraction of Seyfert 2 galaxies with a close neighbor is significantly higher than that of their control (especially within 75 hÀ1 kpc) and Seyfert 1 galaxy samples, confirming a previous two-dimensional analysis of Dultzin-Hacyan et al. We also find that the large-scale environment around the two types of Seyfert galaxies does not vary with respect to their control sample galaxies. -
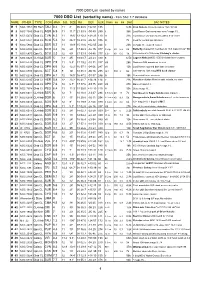
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Ejemplo, Se Detectan En Un Mismo Objeto Líneas De Hierro Una Vez, Y Quince Veces Ionizado
universidad de guanajuato campus guanajuato división de ciencias naturales y exactas DETERMINACIÓNDELAPOBLACIÓNESTELAR ENREGIONESNUCLEARESDEGALAXIASSEYFERT Tesis presentada al posgrado en ciencias (astrofísica) como requisito para la obtención del grado de doctorado en ciencias (astronomía) por juan pablo torres papaqui asesorado por dr. juan pablo torres papaqui Guanajuato, Gto. - Septiembre 2013 RESUMEN Esta tesis reporta el análisis espectroscópico de una muestra de 237 galaxias Seyfert 1, 2, e intermedias, cercanas (z<0.044), cubriendo el rango en longitud de onda de 3500-5200Å. Los espectros fueron obtenidos por mí en el Observatorio Astrofísico Guillermo Haro (OAGH, INAOE, México), y en el NTT del European Southern Ob- servatory (ESO, La Silla, Chile) durante varios períodos de observación. También se cuenta con observaciones tomadas por B.Joguet para su Tesis Doctoral en el telescopio de 1.5 m de La Silla. Casi la mitad de la muestra, 102 galaxias Seyfert de ambos tipos 1 y 2, presentan la serie alta de Balmer en absorción. La primera aportación de este trabajo fue el descubrimiento de las primeras galax- ias Seyfert 1 conteniendo formación estelar reciente importante en su núcleo, co- mo lo evidencia la clara detección en sus espectros de líneas de absorción estelares, pertenecientes a la serie alta de Balmer del Hidrógeno. Este resultado sugiere una reformulación de los actuales modelos ya al detectar formación estelar reciente en los nucleos Seyfert de tipo 1 donde la luz emitida está totalmente dominada por una componente no resuelta espacialmente, podemos inferir que la formacion estelar llega a zonas tan compactas como el mismo núcleo. iii ABSTRACT This thesis reports the spectroscopic analysis of a sample of 237 nearby (z<0.044) galaxies Seyfert types 1, 2 and intermediate.