Lesson 4 MODULE – 3/3 Basic Geometrical Ideas Class: VI Date: 12.6.2020 • Quadrilateral: a Figure Made up of Four Line
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analytic Geometry
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15 -

Models of 2-Dimensional Hyperbolic Space and Relations Among Them; Hyperbolic Length, Lines, and Distances
Models of 2-dimensional hyperbolic space and relations among them; Hyperbolic length, lines, and distances Cheng Ka Long, Hui Kam Tong 1155109623, 1155109049 Course Teacher: Prof. Yi-Jen LEE Department of Mathematics, The Chinese University of Hong Kong MATH4900E Presentation 2, 5th October 2020 Outline Upper half-plane Model (Cheng) A Model for the Hyperbolic Plane The Riemann Sphere C Poincar´eDisc Model D (Hui) Basic properties of Poincar´eDisc Model Relation between D and other models Length and distance in the upper half-plane model (Cheng) Path integrals Distance in hyperbolic geometry Measurements in the Poincar´eDisc Model (Hui) M¨obiustransformations of D Hyperbolic length and distance in D Conclusion Boundary, Length, Orientation-preserving isometries, Geodesics and Angles Reference Upper half-plane model H Introduction to Upper half-plane model - continued Hyperbolic geometry Five Postulates of Hyperbolic geometry: 1. A straight line segment can be drawn joining any two points. 2. Any straight line segment can be extended indefinitely in a straight line. 3. A circle may be described with any given point as its center and any distance as its radius. 4. All right angles are congruent. 5. For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R. Some interesting facts about hyperbolic geometry 1. Rectangles don't exist in hyperbolic geometry. 2. In hyperbolic geometry, all triangles have angle sum < π 3. In hyperbolic geometry if two triangles are similar, they are congruent. -

Angle Chasing
Angle Chasing Ray Li June 12, 2017 1 Facts you should know 1. Let ABC be a triangle and extend BC past C to D: Show that \ACD = \BAC + \ABC: 2. Let ABC be a triangle with \C = 90: Show that the circumcenter is the midpoint of AB: 3. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove that H is the incenter of 4DEF . 4. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove (i) that A; E; F; H lie on a circle diameter AH and (ii) that B; E; F; C lie on a circle with diameter BC. 5. Let ABC be a triangle with circumcenter O and orthocenter H: Show that \BAH = \CAO: 6. Let ABC be a triangle with circumcenter O and orthocenter H and let AH and AO meet the circumcircle at D and E, respectively. Show (i) that H and D are symmetric with respect to BC; and (ii) that H and E are symmetric with respect to the midpoint BC: 7. Let ABC be a triangle with altitudes AD; BE; and CF: Let M be the midpoint of side BC. Show that ME and MF are tangent to the circumcircle of AEF: 8. Let ABC be a triangle with incenter I, A-excenter Ia, and D the midpoint of arc BC not containing A on the circumcircle. Show that DI = DIa = DB = DC: 9. Let ABC be a triangle with incenter I and D the midpoint of arc BC not containing A on the circumcircle. -

Squaring the Circle a Case Study in the History of Mathematics the Problem
Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A. -

10-1 Study Guide and Intervention Circles and Circumference
NAME _____________________________________________ DATE ____________________________ PERIOD _____________ 10-1 Study Guide and Intervention Circles and Circumference Segments in Circles A circle consists of all points in a plane that are a given distance, called the radius, from a given point called the center. A segment or line can intersect a circle in several ways. • A segment with endpoints that are at the center and on the circle is a radius. • A segment with endpoints on the circle is a chord. • A chord that passes through the circle’s center and made up of collinear radii is a diameter. chord: 퐴퐸̅̅̅̅, 퐵퐷̅̅̅̅ radius: 퐹퐵̅̅̅̅, 퐹퐶̅̅̅̅, 퐹퐷̅̅̅̅ For a circle that has radius r and diameter d, the following are true diameter: 퐵퐷̅̅̅̅ 푑 1 r = r = d d = 2r 2 2 Example a. Name the circle. The name of the circle is ⨀O. b. Name radii of the circle. 퐴푂̅̅̅̅, 퐵푂̅̅̅̅, 퐶푂̅̅̅̅, and 퐷푂̅̅̅̅ are radii. c. Name chords of the circle. 퐴퐵̅̅̅̅ and 퐶퐷̅̅̅̅ are chords. Exercises For Exercises 1-7, refer to 1. Name the circle. ⨀R 2. Name radii of the circle. 푹푨̅̅̅̅, 푹푩̅̅̅̅, 푹풀̅̅̅̅, and 푹푿̅̅̅̅ 3. Name chords of the circle. ̅푩풀̅̅̅, 푨푿̅̅̅̅, 푨푩̅̅̅̅, and 푿풀̅̅̅̅ 4. Name diameters of the circle. 푨푩̅̅̅̅, and 푿풀̅̅̅̅ 5. If AB = 18 millimeters, find AR. 9 mm 6. If RY = 10 inches, find AR and AB . AR = 10 in.; AB = 20 in. 7. Is 퐴퐵̅̅̅̅ ≅ 푋푌̅̅̅̅? Explain. Yes; all diameters of the same circle are congruent. Chapter 10 5 Glencoe Geometry NAME _____________________________________________ DATE ____________________________ PERIOD _____________ 10-1 Study Guide and Intervention (continued) Circles and Circumference Circumference The circumference of a circle is the distance around the circle. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

A Historical Introduction to Elementary Geometry
i MATH 119 – Fall 2012: A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning “earth measure” ( ge = earth or land ) + ( metria = measure ) . Euclid wrote the Elements of geometry between 330 and 320 B.C. It was a compilation of the major theorems on plane and solid geometry presented in an axiomatic style. Near the beginning of the first of the thirteen books of the Elements, Euclid enumerated five fundamental assumptions called postulates or axioms which he used to prove many related propositions or theorems on the geometry of two and three dimensions. POSTULATE 1. Any two points can be joined by a straight line. POSTULATE 2. Any straight line segment can be extended indefinitely in a straight line. POSTULATE 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. POSTULATE 4. All right angles are congruent. POSTULATE 5. (Parallel postulate) If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. The circle described in postulate 3 is tacitly unique. Postulates 3 and 5 hold only for plane geometry; in three dimensions, postulate 3 defines a sphere. Postulate 5 leads to the same geometry as the following statement, known as Playfair's axiom, which also holds only in the plane: Through a point not on a given straight line, one and only one line can be drawn that never meets the given line. -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -

Find the Radius Or Diameter of the Circle with the Given Dimensions. 2
8-1 Circumference Find the radius or diameter of the circle with the given dimensions. 2. d = 24 ft SOLUTION: The radius is 12 feet. ANSWER: 12 ft Find the circumference of the circle. Use 3.14 or for π. Round to the nearest tenth if necessary. 4. SOLUTION: The circumference of the circle is about 25.1 feet. ANSWER: 3.14 × 8 = 25.1 ft eSolutions Manual - Powered by Cognero Page 1 8-1 Circumference 6. SOLUTION: The circumference of the circle is about 22 miles. ANSWER: 8. The Belknap shield volcano is located in the Cascade Range in Oregon. The volcano is circular and has a diameter of 5 miles. What is the circumference of this volcano to the nearest tenth? SOLUTION: The circumference of the volcano is about 15.7 miles. ANSWER: 15.7 mi eSolutions Manual - Powered by Cognero Page 2 8-1 Circumference Copy and Solve Show your work on a separate piece of paper. Find the diameter given the circumference of the object. Use 3.14 for π. 10. a satellite dish with a circumference of 957.7 meters SOLUTION: The diameter of the satellite dish is 305 meters. ANSWER: 305 m 12. a nickel with a circumference of about 65.94 millimeters SOLUTION: The diameter of the nickel is 21 millimeters. ANSWER: 21 mm eSolutions Manual - Powered by Cognero Page 3 8-1 Circumference Find the distance around the figure. Use 3.14 for π. 14. SOLUTION: The distance around the figure is 5 + 5 or 10 feet plus of the circumference of a circle with a radius of 5 feet. -

3.1 the Robertson-Walker Metric
M. Pettini: Introduction to Cosmology | Lecture 3 RELATIVISTIC COSMOLOGY 3.1 The Robertson-Walker Metric The appearance of objects at cosmological distances is affected by the curvature of spacetime through which light travels on its way to Earth. The most complete description of the geometrical properties of the Universe is provided by Einstein's general theory of relativity. In GR, the fundamental quantity is the metric which describes the geometry of spacetime. Let's look at the definition of a metric: in 3-D space we measure the distance along a curved path P between two points using the differential distance formula, or metric: (d`)2 = (dx)2 + (dy)2 + (dz)2 (3.1) and integrating along the path P (a line integral) to calculate the total distance: Z 2 q Z 2 q ∆` = (d`)2 = (dx)2 + (dy)2 + (dz)2 (3.2) 1 1 Similarly, to measure the interval along a curved wordline, W, connecting two events in spacetime with no mass present, we use the metric for flat spacetime: (ds)2 = (cdt)2 − (dx)2 − (dy)2 − (dz)2 (3.3) Integrating ds gives the total interval along the worldline W: Z B q Z B q ∆s = (ds)2 = (cdt)2 − (dx)2 − (dy)2 − (dz)2 (3.4) A A By definition, the distance measured between two events, A and B, in a reference frame for which they occur simultaneously (tA = tB) is the proper distance: q ∆L = −(∆s)2 (3.5) Our search for a metric that describes the spacetime of a matter-filled universe, is made easier by the cosmological principle. -
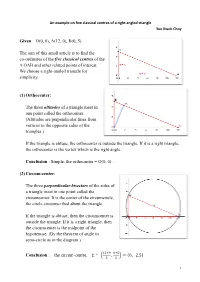
An Example on Five Classical Centres of a Right Angled Triangle
An example on five classical centres of a right angled triangle Yue Kwok Choy Given O(0, 0), A(12, 0), B(0, 5) . The aim of this small article is to find the co-ordinates of the five classical centres of the ∆ OAB and other related points of interest. We choose a right-angled triangle for simplicity. (1) Orthocenter: The three altitudes of a triangle meet in one point called the orthocenter. (Altitudes are perpendicular lines from vertices to the opposite sides of the triangles.) If the triangle is obtuse, the orthocenter is outside the triangle. If it is a right triangle, the orthocenter is the vertex which is the right angle. Conclusion : Simple, the orthocenter = O(0, 0) . (2) Circum-center: The three perpendicular bisectors of the sides of a triangle meet in one point called the circumcenter. It is the center of the circumcircle, the circle circumscribed about the triangle. If the triangle is obtuse, then the circumcenter is outside the triangle. If it is a right triangle, then the circumcenter is the midpoint of the hypotenuse. (By the theorem of angle in semi-circle as in the diagram.) Conclusion : the circum -centre, E = ͥͦͮͤ ͤͮͩ ʠ ͦ , ͦ ʡ Ɣ ʚ6, 2.5ʛ 1 Exercise 1: (a) Check that the circum -circle above is given by: ͦ ͦ ͦ. ʚx Ǝ 6ʛ ƍ ʚy Ǝ 2.5ʛ Ɣ 6.5 (b) Show that t he area of the triangle with sides a, b, c and angles A, B, C is ΏΐΑ ͦ , where R is the radius of the circum -circle . -

Chapter 1. the Medial Triangle 2
Chapter 1. The Medial Triangle 2 The triangle formed by joining the midpoints of the sides of a given triangle is called the me- dial triangle. Let A1B1C1 be the medial trian- gle of the triangle ABC in Figure 1. The sides of A1B1C1 are parallel to the sides of ABC and 1 half the lengths. So A B C is the area of 1 1 1 4 ABC. Figure 1: In fact area(AC1B1) = area(A1B1C1) = area(C1BA1) 1 = area(B A C) = area(ABC): 1 1 4 Figure 2: The quadrilaterals AC1A1B1 and C1BA1B1 are parallelograms. Thus the line segments AA1 and C1B1 bisect one another, and the line segments BB1 and CA1 bisect one another. (Figure 2) Figure 3: Thus the medians of A1B1C1 lie along the medians of ABC, so both tri- angles A1B1C1 and ABC have the same centroid G. 3 Now draw the altitudes of A1B1C1 from vertices A1 and C1. (Figure 3) These altitudes are perpendicular bisectors of the sides BC and AB of the triangle ABC so they intersect at O, the circumcentre of ABC. Thus the orthocentre of A1B1C1 coincides with the circumcentre of ABC. Let H be the orthocentre of the triangle ABC, that is the point of intersection of the altitudes of ABC. Two of these altitudes AA2 and BB2 are shown. (Figure 4) Since O is the orthocen- tre of A1B1C1 and H is the orthocentre of ABC then jAHj = 2jA1Oj Figure 4: . The centroid G of ABC lies on AA1 and jAGj = 2jGA1j . We also have AA2kOA1, since O is the orthocentre of A1B1C1.