Cap Products, Orientations, Künneth Formula
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Surfaces and Fundamental Groups
HOMEWORK 5 — SURFACES AND FUNDAMENTAL GROUPS DANNY CALEGARI This homework is due Wednesday November 22nd at the start of class. Remember that the notation e1; e2; : : : ; en w1; w2; : : : ; wm h j i denotes the group whose generators are equivalence classes of words in the generators ei 1 and ei− , where two words are equivalent if one can be obtained from the other by inserting 1 1 or deleting eiei− or ei− ei or by inserting or deleting a word wj or its inverse. Problem 1. Let Sn be a surface obtained from a regular 4n–gon by identifying opposite sides by a translation. What is the Euler characteristic of Sn? What surface is it? Find a presentation for its fundamental group. Problem 2. Let S be the surface obtained from a hexagon by identifying opposite faces by translation. Then the fundamental group of S should be given by the generators a; b; c 1 1 1 corresponding to the three pairs of edges, with the relation abca− b− c− coming from the boundary of the polygonal region. What is wrong with this argument? Write down an actual presentation for π1(S; p). What surface is S? Problem 3. The four–color theorem of Appel and Haken says that any map in the plane can be colored with at most four distinct colors so that two regions which share a com- mon boundary segment have distinct colors. Find a cell decomposition of the torus into 7 polygons such that each two polygons share at least one side in common. Remark. -

Problem Set 10 ETH Zürich FS 2020
d-math Topology ETH Zürich Prof. A. Carlotto Solutions - Problem set 10 FS 2020 10. Computing the fundamental group - Part I Chef’s table This week we start computing fundamental group, mainly using Van Kampen’s Theorem (but possibly in combination with other tools). The first two problems are sort of basic warm-up exercises to get a feeling for the subject. Problems 10.3 - 10.4 - 10.5 are almost identical, and they all build on the same trick (think in terms of the planar models!); you can write down the solution to just one of them, but make sure you give some thought about all. From there (so building on these results), using Van Kampen you can compute the fundamental group of the torus (which we knew anyway, but through a different method), of the Klein bottle and of higher-genus surfaces. Problem 10.8 is the most important in this series, and learning this trick will trivialise half of the problems on this subject (see Problem 10.9 for a first, striking, application); writing down all homotopies of 10.8 explicitly might be a bit tedious, so just make sure to have a clear picture (and keep in mind this result for the future). 10.1. Topological manifold minus a point L. Let X be a connected topological ∼ manifold, of dimension n ≥ 3. Prove that for every x ∈ X one has π1(X) = π1(X \{x}). 10.2. Plane without the circle L. Show that there is no homeomorphism f : R2 \S1 → R2 \ S1 such that f(0, 0) = (2, 0). -

On the Classification of Heegaard Splittings
Manuscript (Revised) ON THE CLASSIFICATION OF HEEGAARD SPLITTINGS TOBIAS HOLCK COLDING, DAVID GABAI, AND DANIEL KETOVER Abstract. The long standing classification problem in the theory of Heegaard splittings of 3-manifolds is to exhibit for each closed 3-manifold a complete list, without duplication, of all its irreducible Heegaard surfaces, up to isotopy. We solve this problem for non Haken hyperbolic 3-manifolds. 0. Introduction The main result of this paper is Theorem 0.1. Let N be a closed non Haken hyperbolic 3-manifold. There exists an effec- tively constructible set S0;S1; ··· ;Sn such that if S is an irreducible Heegaard splitting, then S is isotopic to exactly one Si. Remarks 0.2. Given g 2 N Tao Li [Li3] shows how to construct a finite list of genus-g Heegaard surfaces such that, up to isotopy, every genus-g Heegaard surface appears in that list. By [CG] there exists an effectively computable C(N) such that one need only consider g ≤ C(N), hence there exists an effectively constructible set of Heegaard surfaces that contains every irreducible Heegaard surface. (The methods of [CG] also effectively constructs these surfaces.) However, this list may contain reducible splittings and duplications. The main goal of this paper is to give an effective algorithm that weeds out the duplications and reducible splittings. Idea of Proof. We first prove the Thick Isotopy Lemma which implies that if Si is isotopic to Sj, then there exists a smooth isotopy by surfaces of area uniformly bounded above and diametric soul uniformly bounded below. (The diametric soul of a surface T ⊂ N is the infimal diameter in N of the essential closed curves in T .) The proof of this lemma uses a 2-parameter sweepout argument that may be of independent interest. -

Lecture 1 Rachel Roberts
Lecture 1 Rachel Roberts Joan Licata May 13, 2008 The following notes are a rush transcript of Rachel’s lecture. Any mistakes or typos are mine, and please point these out so that I can post a corrected copy online. Outline 1. Three-manifolds: Presentations and basic structures 2. Foliations, especially codimension 1 foliations 3. Non-trivial examples of three-manifolds, generalizations of foliations to laminations 1 Three-manifolds Unless otherwise noted, let M denote a closed (compact) and orientable three manifold with empty boundary. (Note that these restrictions are largely for convenience.) We’ll start by collecting some useful facts about three manifolds. Definition 1. For our purposes, a triangulation of M is a decomposition of M into a finite colleciton of tetrahedra which meet only along shared faces. Fact 1. Every M admits a triangulation. This allows us to realize any M as three dimensional simplicial complex. Fact 2. M admits a C ∞ structure which is unique up to diffeomorphism. We’ll work in either the C∞ or PL category, which are equivalent for three manifolds. In partuclar, we’ll rule out wild (i.e. pathological) embeddings. 2 Examples 1. S3 (Of course!) 2. S1 × S2 3. More generally, for F a closed orientable surface, F × S1 1 Figure 1: A Heegaard diagram for the genus four splitting of S3. Figure 2: Left: Genus one Heegaard decomposition of S3. Right: Genus one Heegaard decomposi- tion of S2 × S1. We’ll begin by studying S3 carefully. If we view S3 as compactification of R3, we can take a neighborhood of the origin, which is a solid ball. -

Approximation Algorithms for Euler Genus and Related Problems
Approximation algorithms for Euler genus and related problems Chandra Chekuri Anastasios Sidiropoulos February 3, 2014 Slides based on a presentation of Tasos Sidiropoulos Theorem (Kuratowski, 1930) A graph is planar if and only if it does not contain K5 and K3;3 as a topological minor. Theorem (Wagner, 1937) A graph is planar if and only if it does not contain K5 and K3;3 as a minor. Graphs and topology Theorem (Wagner, 1937) A graph is planar if and only if it does not contain K5 and K3;3 as a minor. Graphs and topology Theorem (Kuratowski, 1930) A graph is planar if and only if it does not contain K5 and K3;3 as a topological minor. Graphs and topology Theorem (Kuratowski, 1930) A graph is planar if and only if it does not contain K5 and K3;3 as a topological minor. Theorem (Wagner, 1937) A graph is planar if and only if it does not contain K5 and K3;3 as a minor. Minors and Topological minors Definition A graph H is a minor of G if H is obtained from G by a sequence of edge/vertex deletions and edge contractions. Definition A graph H is a topological minor of G if a subdivision of H is isomorphic to a subgraph of G. Planarity planar graph non-planar graph Planarity planar graph non-planar graph g = 0 g = 1 g = 2 g = 3 k = 1 k = 2 What about other surfaces? sphere torus double torus triple torus real projective plane Klein bottle What about other surfaces? sphere torus double torus triple torus g = 0 g = 1 g = 2 g = 3 real projective plane Klein bottle k = 1 k = 2 Genus of graphs Definition The orientable (reps. -
![Arxiv:1912.13021V1 [Math.GT] 30 Dec 2019 on Small, Compact 4-Manifolds While Also Constraining Their Handle Structures and Piecewise- Linear Topology](https://docslib.b-cdn.net/cover/0303/arxiv-1912-13021v1-math-gt-30-dec-2019-on-small-compact-4-manifolds-while-also-constraining-their-handle-structures-and-piecewise-linear-topology-1820303.webp)
Arxiv:1912.13021V1 [Math.GT] 30 Dec 2019 on Small, Compact 4-Manifolds While Also Constraining Their Handle Structures and Piecewise- Linear Topology
The trace embedding lemma and spinelessness Kyle Hayden Lisa Piccirillo We demonstrate new applications of the trace embedding lemma to the study of piecewise- linear surfaces and the detection of exotic phenomena in dimension four. We provide infinitely many pairs of homeomorphic 4-manifolds W and W 0 homotopy equivalent to S2 which have smooth structures distinguished by several formal properties: W 0 is diffeomor- phic to a knot trace but W is not, W 0 contains S2 as a smooth spine but W does not even contain S2 as a piecewise-linear spine, W 0 is geometrically simply connected but W is not, and W 0 does not admit a Stein structure but W does. In particular, the simple spineless 4-manifolds W provide an alternative to Levine and Lidman's recent solution to Problem 4.25 in Kirby's list. We also show that all smooth 4-manifolds contain topological locally flat surfaces that cannot be approximated by piecewise-linear surfaces. 1 Introduction In 1957, Fox and Milnor observed that a knot K ⊂ S3 arises as the link of a singularity of a piecewise-linear 2-sphere in S4 with one singular point if and only if K bounds a smooth disk in B4 [17, 18]; such knots are now called slice. Any such 2-sphere has a neighborhood diffeomorphic to the zero-trace of K , where the n-trace is the 4-manifold Xn(K) obtained from B4 by attaching an n-framed 2-handle along K . In this language, Fox and Milnor's 3 4 observation says that a knot K ⊂ S is slice if and only if X0(K) embeds smoothly in S (cf [35, 42]). -
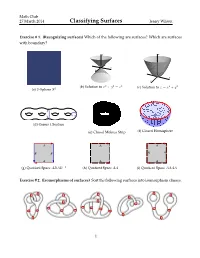
Classifying Surfaces Jenny Wilson
Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Exercise # 1. (Recognizing surfaces) Which of the following are surfaces? Which are surfaces with boundary? z z y x y x (b) Solution to x2 + y2 = z2 (c) Solution to z = x2 + y2 (a) 2–Sphere S2 (d) Genus 4 Surface (e) Closed Mobius Strip (f) Closed Hemisphere A A A BB A A A A A (g) Quotient Space ABAB−1 (h) Quotient Space AA (i) Quotient Space AAAA Exercise # 2. (Isomorphisms of surfaces) Sort the following surfaces into isomorphism classes. 1 Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Exercise # 3. (Quotient surfaces) Identify among the following quotient spaces: a cylinder, a Mobius¨ band, a sphere, a torus, real projective space, and a Klein bottle. A A A A BB A B BB A A B A Exercise # 4. (Gluing Mobius bands) How many boundary components does a Mobius band have? What surface do you get by gluing two Mobius bands along their boundary compo- nents? Exercise # 5. (More quotient surfaces) Identify the following surfaces. A A BB A A h h g g Triangulations Exercise # 6. (Minimal triangulations) What is the minimum number of triangles needed to triangulate a sphere? A cylinder? A torus? 2 Math Club 27 March 2014 Classifying Surfaces Jenny Wilson Orientability Exercise # 7. (Orientability is well-defined) Fix a surface S. Prove that if one triangulation of S is orientable, then all triangulations of S are orientable. Exercise # 8. (Orientability) Prove that the disk, sphere, and torus are orientable. Prove that the Mobius strip and Klein bottle are nonorientiable. -

On Real Projective Connections, VI Smirnov's Approach, and Black Hole
ON REAL PROJECTIVE CONNECTIONS, V.I. SMIRNOV’S APPROACH, AND BLACK HOLE TYPE SOLUTIONS OF THE LIOUVILLE EQUATION LEON A. TAKHTAJAN Dedicated to my teacher Ludwig Dmitrievich Faddeev on the occasion of his 80th birthday Abstract. We consider real projective connections on Riemann sur- faces and their corresponding solutions of the Liouville equation. We show that these solutions have singularities of special type (a black-hole type) on a finite number of simple analytical contours. We analyze the case of the Riemann sphere with four real punctures, considered in V.I. Smirnov’s thesis (Petrograd, 1918), in detail. 1. Introduction One of the central problems of mathematics in the second half of the 19th century and at the beginning of the 20th century was the problem of uniformization of Riemann surfaces. The classics, Klein [1] and Poincar´e [2], associated it with studying second-order ordinary differential equations with regular singular points. Poincar´eproposed another approach to the uniformization problem [3]. It consists in finding a complete conformal met- ric of constant negative curvature, and it reduces to the global solvability of the Liouville equation, a special nonlinear partial differential equations of elliptic type on a Riemann surface. Here, we illustrate the relation between these two approaches and describe solutions of the Liouville equation corresponding to second-order ordinary differential equations with a real monodromy group. In the modern physics arXiv:1407.1815v2 [math.CV] 9 Jan 2015 literature on the Liouville equation it is rather commonly assumed that for the Fuchsian uniformization of a Riemann surface it suffices to have a second-order ordinary differential equation with a real monodromy group. -

Real Compact Surfaces
GENERAL I ARTICLE Real Compact Surfaces A lexandru Oancea Alexandru Oancea studies The classification of real compact surfaces is a main result in ENS, Paris and is which is at the same time easy to understand and non currently pursuing his trivial, simple in formulation and rich in consequences. doctoral work at Univ. The aim of this article is to explain the theorem by means Paris Sud, Orsay, France. He visited the Chennai of many drawings. It is an invitation to a visual approach of Mathematical Institute, mathematics. Chennai in 2000 as part of ENS-CMI exchange First Definitions and Examples programme. We assume that the reader has already encountered the notion of a topology on a set X. Roughly speaking this enables one to recognize points that are 'close' to a given point x E X. Continuous fu'nctions between topological spaces are functions that send 'close' points to 'close' points. We can also see this on their graph: • The graph of a continuous function f: R-7R can be drawn without raising the pencil from the drawing paper. • The graph of a continuous function!: R 2 -7 R can be thought of as a tablecloth which is not tom. • The graph of a continuous map between topological spaces f' X -7 Y is closed in the product space. X x Y. The most familiar topological space is the n-dimensional euclid ean space Rn. It will be the hidden star of the present article, which is devoted to a rich generalization of this kind of space, namely manifolds. -

Geometry of Algebraic Curves
Geometry of Algebraic Curves Lectures delivered by Joe Harris Notes by Akhil Mathew Fall 2011, Harvard Contents Lecture 1 9/2 x1 Introduction 5 x2 Topics 5 x3 Basics 6 x4 Homework 11 Lecture 2 9/7 x1 Riemann surfaces associated to a polynomial 11 x2 IOUs from last time: the degree of KX , the Riemann-Hurwitz relation 13 x3 Maps to projective space 15 x4 Trefoils 16 Lecture 3 9/9 x1 The criterion for very ampleness 17 x2 Hyperelliptic curves 18 x3 Properties of projective varieties 19 x4 The adjunction formula 20 x5 Starting the course proper 21 Lecture 4 9/12 x1 Motivation 23 x2 A really horrible answer 24 x3 Plane curves birational to a given curve 25 x4 Statement of the result 26 Lecture 5 9/16 x1 Homework 27 x2 Abel's theorem 27 x3 Consequences of Abel's theorem 29 x4 Curves of genus one 31 x5 Genus two, beginnings 32 Lecture 6 9/21 x1 Differentials on smooth plane curves 34 x2 The more general problem 36 x3 Differentials on general curves 37 x4 Finding L(D) on a general curve 39 Lecture 7 9/23 x1 More on L(D) 40 x2 Riemann-Roch 41 x3 Sheaf cohomology 43 Lecture 8 9/28 x1 Divisors for g = 3; hyperelliptic curves 46 x2 g = 4 48 x3 g = 5 50 1 Lecture 9 9/30 x1 Low genus examples 51 x2 The Hurwitz bound 52 2.1 Step 1 . 53 2.2 Step 10 ................................. 54 2.3 Step 100 ................................ 54 2.4 Step 2 . -

Heegaard-Floer Homology; a Brief Introduction
Heegaard-Floer homology; a brief introduction Jesse Frohlich April 29, 2019 1 Introduction Heegaard-Floer homology, like most homology theories, takes in a geometric or topological structure and gives a (graded) abelian group. In this case, the geometric object is a closed, oriented 3-manifold Y . A generalization can be applied to a knot K in a 3-manifold; the machinery of Heegaard-Floer homology is able to determine the genus of the knot (being the minimal genus of a surface with boundary K (after gluing a disk over the boundary)), which in particular can distinguish the unknot from all other knots. 2 Construction To build the homology groups, we begin by expressing the 3-manifold in simpler terms: Definition. A genus g handlebody is a 3-manifold M, whose boundary @M is homeomorphic to the genus g surface Σg (which is unique up to homeomorphism). Our goal is to reduce our study to gluings of handlebodies. Given a 3-manifold Y , we want to decompose it as a union of handlebodies. Definition. A Heegaard splitting of Y is a pair of handlebodies U0, U1 ⊆ Y which are embedded submanifolds with boundary which have as a common boundary a genus-g surface Σg ⊆ Y . 1 Given a model genus g handlebody U, we can describe Y as a pair of embeddings 'i : U,! Y . Up to homeomorphism, these embeddings are determined by how 'i restricts to Σ := @U. Further 'ijΣ is determined by a collection of curves in 'i(Σ) which are contractible in 'i(U). From this, we get: Definition. -

Euler Characteristics of Surfaces
Euler characteristics of surfaces Shirley Wang Advisor: Eugene Gorsky Mathematics Department UC Davis May 25, 2021 Contents 1 Introduction 1 2 Euler characteristic on a given surface 1 3 Examples of surfaces 10 3.1 Orientable surfaces . 11 3.2 Unorientable surfaces . 13 3.3 Classification of surfaces . 16 4 Acknowledgements 17 1 Introduction In this note we study Euler characteristics of surfaces and graphs on them. The Euler characteristic of a graph G is defined as χ(G) = V − E + F where V; E and F are respectively the numbers of vertices, edges and faces of a graph G. In section 2, we discuss χ of graphs on a given surface. First, we prove Theorem 2.1 about the Euler characteristic of a planar graph with k connected components. Then, we move to the case where k = 1 (i.e when the graph is connected) but the surface is arbitrary and prove in Theorem 2.5 that χ is independent of the choice of a (connected) graph we have on a given surface, and we will provide two methods for doing so. We define the Euler characteristic χ(S) of a surface S as the Euler characteristic of arbitrary (good) graph on S. In section 3, we study the Euler Characteristics of various surfaces. We will introduce orientability (and non-orientability), connected sum of two surfaces, and classification of surfaces. The exposition mainly follows Chapter 4 in [1]. 2 Euler characteristic on a given surface In this section, we want to show that Euler characteristic is the same for any good graph on a given surface (could be any, e.g torus, sphere,etc).