DOCSLIB.ORG

PGI Fortran Reference Copyright © 2005, Stmicroelectronics, Inc

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PGI Fortran Reference Copyright © 2005, Stmicroelectronics, Inc PGI® Fortran Reference The Portland Group STMicroelectronics 9150 SW Pioneer Court, Suite H Wilsonville, OR 97070 www.pgroup.com While every precaution has been taken in the preparation of this document, The Portland Group™, a wholly-owned subsidiary of STMicroelectronics, makes no warranty for the use of its products and assumes no responsibility for any errors that may appear, or for damages resulting from the use of the information contained herein. STMicroelectronics retains the right to make changes to this information at any time, without notice. The software described in this document is distributed under license from STMicroelectronics and may be used or copied only in accordance with the terms of the license agreement. No part of this document may be reproduced or transmitted in any form or by any means, for any purpose other than the purchaser's personal use without the express written permission of STMicroelectronics. Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this manual, STMicroelectronics was aware of a trademark claim. The designations have been printed in caps or initial caps. Thanks is given to the Parallel Tools Consortium and, in particular, to the High Performance Debugging Forum for their efforts. PGF90, PGF95, PGC++, Cluster Development Kit, CDK and The Portland Group are trademarks and PGI, PGHPF, PGF77, PGCC, PGPROF, and PGDBG are registered trademarks of STMicroelectronics, Inc. Other brands and names are the property of their respective owners. The use of STLport, a C++ Library, is licensed separately and license, distribution and copyright notice can be found in online documentation for a given release of the PGI compilers and tools. PGI Fortran Reference Copyright © 2005, STMicroelectronics, Inc. All rights reserved. Printed in the United States of America First Printing: Release 6.0, March, 2005 Part Number: 2410-990-990-0297 Technical support: [email protected] Sales: [email protected] Web: www.pgroup.com Table of Contents PREFACE......................................................................................................................................15 AUDIENCE DESCRIPTION..............................................................................................................15 COMPATIBILITY AND CONFORMANCE TO STANDARDS.................................................................15 ORGANIZATION............................................................................................................................16 HARDWARE AND SOFTWARE CONSTRAINTS ................................................................................17 CONVENTIONS .............................................................................................................................17 RELATED PUBLICATIONS .............................................................................................................18 1 LANGUAGE OVERVIEW..................................................................................................20 1.1 ELEMENTS OF A FORTRAN PROGRAM UNIT......................................................................20 1.1.1 Statements ...............................................................................................................20 1.1.2 Free and Fixed Source ............................................................................................21 1.1.3 Statement Ordering .................................................................................................21 1.2 THE FORTRAN CHARACTER SET ......................................................................................22 1.3 FREE FORM FORMATTING ................................................................................................23 1.4 FIXED FORMATTING.........................................................................................................24 1.4.1 Column Formatting.................................................................................................24 1.4.2 Fixed Format Label Field .......................................................................................24 1.4.3 Fixed Format Continuation Field ...........................................................................24 1.4.4 Fixed Format Statement Field.................................................................................25 1.4.5 Fixed Format Debug Statements.............................................................................25 1.4.6 Tab Formatting .......................................................................................................25 1.4.7 Fixed Input File Format – Summary.......................................................................25 1.5 INCLUDING FORTRAN SOURCE FILES ...............................................................................26 1.6 THE COMPONENTS OF FORTRAN STATEMENTS ................................................................26 1.6.1 Symbolic Names ......................................................................................................27 1.7 EXPRESSIONS ...................................................................................................................27 1.7.1 Expression Precedence Rules..................................................................................28 1.7.2 Arithmetic Expressions............................................................................................29 1.7.3 Relational Expressions............................................................................................30 1.7.4 Logical Expressions ................................................................................................31 1.7.5 Character Expressions ............................................................................................32 1.7.6 Character Concatenation........................................................................................32 1.8 SYMBOLIC NAME SCOPE..................................................................................................32 1.9 ASSIGNMENT STATEMENTS..............................................................................................32 1.9.1 Arithmetic Assignment ...................................................................................................33 1.9.2 Logical Assignment Statement .......................................................................................33 1.9.3 Character Assignment....................................................................................................34 1.10 LISTING CONTROLS..........................................................................................................35 1.11 OPENMP DIRECTIVES ......................................................................................................35 1.12 HPF DIRECTIVES .............................................................................................................35 i 2 FORTRAN DATA TYPES................................................................................................... 37 2.1 INTRINSIC DATA TYPES ................................................................................................... 37 2.1.1 Kind Parameter....................................................................................................... 37 2.1.2 Number of Bytes Specification ................................................................................ 38 2.2 CONSTANTS ..................................................................................................................... 40 2.2.1 Integer Constants.................................................................................................... 40 2.2.2 Binary, Octal and Hexadecimal Constants............................................................. 41 2.2.3 Real Constants ........................................................................................................ 41 2.2.4 Integer Constants.................................................................................................... 42 2.2.5 Complex Constants ................................................................................................. 42 2.2.6 Logical Constants ................................................................................................... 43 2.2.7 Character Constants ............................................................................................... 43 2.2.8 PARAMETER Constants......................................................................................... 44 2.3 DERIVED TYPES............................................................................................................... 44 2.4 ARRAYS........................................................................................................................... 45 2.4.1 An Array Declaration Element ............................................................................... 45 2.4.2 Deferred Shape Arrays ........................................................................................... 46 2.4.3 Subscripts................................................................................................................ 46 2.4.4 Character Substring................................................................................................ 46 2.5 FORTRAN POINTERS AND TARGETS ................................................................................. 47 2.6 FORTRAN BINARY, OCTAL AND HEXADECIMAL
Load more

Recommended publications
  • Fortran 90 Overview
    1 Fortran 90 Overview J.E. Akin, Copyright 1998 This overview of Fortran 90 (F90) features is presented as a series of tables that illustrate the syntax and abilities of F90. Frequently comparisons are made to similar features in the C++ and F77 languages and to the Matlab environment. These tables show that F90 has significant improvements over F77 and matches or exceeds newer software capabilities found in C++ and Matlab for dynamic memory management, user defined data structures, matrix operations, operator definition and overloading, intrinsics for vector and parallel pro- cessors and the basic requirements for object-oriented programming. They are intended to serve as a condensed quick reference guide for programming in F90 and for understanding programs developed by others. List of Tables 1 Comment syntax . 4 2 Intrinsic data types of variables . 4 3 Arithmetic operators . 4 4 Relational operators (arithmetic and logical) . 5 5 Precedence pecking order . 5 6 Colon Operator Syntax and its Applications . 5 7 Mathematical functions . 6 8 Flow Control Statements . 7 9 Basic loop constructs . 7 10 IF Constructs . 8 11 Nested IF Constructs . 8 12 Logical IF-ELSE Constructs . 8 13 Logical IF-ELSE-IF Constructs . 8 14 Case Selection Constructs . 9 15 F90 Optional Logic Block Names . 9 16 GO TO Break-out of Nested Loops . 9 17 Skip a Single Loop Cycle . 10 18 Abort a Single Loop . 10 19 F90 DOs Named for Control . 10 20 Looping While a Condition is True . 11 21 Function definitions . 11 22 Arguments and return values of subprograms . 12 23 Defining and referring to global variables .
    [Show full text]
  • Quick Overview: Complex Numbers
    Quick Overview: Complex Numbers February 23, 2012 1 Initial Definitions Definition 1 The complex number z is defined as: z = a + bi (1) p where a, b are real numbers and i = −1. Remarks about the definition: • Engineers typically use j instead of i. • Examples of complex numbers: p 5 + 2i; 3 − 2i; 3; −5i • Powers of i: i2 = −1 i3 = −i i4 = 1 i5 = i i6 = −1 i7 = −i . • All real numbers are also complex (by taking b = 0). 2 Visualizing Complex Numbers A complex number is defined by it's two real numbers. If we have z = a + bi, then: Definition 2 The real part of a + bi is a, Re(z) = Re(a + bi) = a The imaginary part of a + bi is b, Im(z) = Im(a + bi) = b 1 Im(z) 4i 3i z = a + bi 2i r b 1i θ Re(z) a −1i Figure 1: Visualizing z = a + bi in the complex plane. Shown are the modulus (or length) r and the argument (or angle) θ. To visualize a complex number, we use the complex plane C, where the horizontal (or x-) axis is for the real part, and the vertical axis is for the imaginary part. That is, a + bi is plotted as the point (a; b). In Figure 1, we can see that it is also possible to represent the point a + bi, or (a; b) in polar form, by computing its modulus (or size), and angle (or argument): p r = jzj = a2 + b2 θ = arg(z) We have to be a bit careful defining φ, since there are many ways to write φ (and we could add multiples of 2π as well).
    [Show full text]
  • Z/OS ISPF Services Guide COMMAND NAME
    z/OS 2.4 ISPF Services Guide IBM SC19-3626-40 Note Before using this information and the product it supports, read the information in “Notices” on page 399. This edition applies to Version 2 Release 4 of z/OS (5650-ZOS) and to all subsequent releases and modifications until otherwise indicated in new editions. Last updated: 2021-06-22 © Copyright International Business Machines Corporation 1980, 2021. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents Figures................................................................................................................ xv Tables................................................................................................................xvii Preface...............................................................................................................xix Who should use this document?............................................................................................................... xix What is in this document?......................................................................................................................... xix How to read the syntax diagrams..............................................................................................................xix z/OS information...............................................................................................xxiii How to send your comments to IBM...................................................................
    [Show full text]
  • Fortran Math Special Functions Library
    IMSL® Fortran Math Special Functions Library Version 2021.0 Copyright 1970-2021 Rogue Wave Software, Inc., a Perforce company. Visual Numerics, IMSL, and PV-WAVE are registered trademarks of Rogue Wave Software, Inc., a Perforce company. IMPORTANT NOTICE: Information contained in this documentation is subject to change without notice. Use of this docu- ment is subject to the terms and conditions of a Rogue Wave Software License Agreement, including, without limitation, the Limited Warranty and Limitation of Liability. ACKNOWLEDGMENTS Use of the Documentation and implementation of any of its processes or techniques are the sole responsibility of the client, and Perforce Soft- ware, Inc., assumes no responsibility and will not be liable for any errors, omissions, damage, or loss that might result from any use or misuse of the Documentation PERFORCE SOFTWARE, INC. MAKES NO REPRESENTATION ABOUT THE SUITABILITY OF THE DOCUMENTATION. THE DOCU- MENTATION IS PROVIDED "AS IS" WITHOUT WARRANTY OF ANY KIND. PERFORCE SOFTWARE, INC. HEREBY DISCLAIMS ALL WARRANTIES AND CONDITIONS WITH REGARD TO THE DOCUMENTATION, WHETHER EXPRESS, IMPLIED, STATUTORY, OR OTHERWISE, INCLUDING WITHOUT LIMITATION ANY IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PAR- TICULAR PURPOSE, OR NONINFRINGEMENT. IN NO EVENT SHALL PERFORCE SOFTWARE, INC. BE LIABLE, WHETHER IN CONTRACT, TORT, OR OTHERWISE, FOR ANY SPECIAL, CONSEQUENTIAL, INDIRECT, PUNITIVE, OR EXEMPLARY DAMAGES IN CONNECTION WITH THE USE OF THE DOCUMENTATION. The Documentation is subject to change at any time without notice. IMSL https://www.imsl.com/ Contents Introduction The IMSL Fortran Numerical Libraries . 1 Getting Started . 2 Finding the Right Routine . 3 Organization of the Documentation . 4 Naming Conventions .
    [Show full text]
  • TSO/E Programming Guide
    z/OS Version 2 Release 3 TSO/E Programming Guide IBM SA32-0981-30 Note Before using this information and the product it supports, read the information in “Notices” on page 137. This edition applies to Version 2 Release 3 of z/OS (5650-ZOS) and to all subsequent releases and modifications until otherwise indicated in new editions. Last updated: 2019-02-16 © Copyright International Business Machines Corporation 1988, 2017. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents List of Figures....................................................................................................... ix List of Tables........................................................................................................ xi About this document...........................................................................................xiii Who should use this document.................................................................................................................xiii How this document is organized............................................................................................................... xiii How to use this document.........................................................................................................................xiii Where to find more information................................................................................................................ xiii How to send your comments to IBM......................................................................xv
    [Show full text]
  • IEEE Standard 754 for Binary Floating-Point Arithmetic
    Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite
    [Show full text]
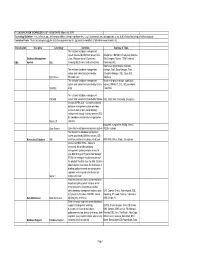
  • TECHNOLOGY LIST - ISSUE DATE: March 18, 2019 Technology Definition: a Set of Knowledge, Skills And/Or Abilities, Taking a Significant Time (E.G
    IT CLASSIFICATION TECHNOLOGY LIST - ISSUE DATE: March 18, 2019 Technology Definition: A set of knowledge, skills and/or abilities, taking a significant time (e.g. 6 months) to learn, and applicable to the defined classification specification assigned. Example of Tools: These are examples only for illustration purposes and are not meant to constitute a full and/or comprehensive list. Classification Discipline Technology Definition Example of Tools The relational database management system provided by IBM that runs on Unix, Omegamon, IBM Admin Tools, Log Analyzer, Database Management Linux, Windows and z/OS platforms DB2 Compare, Nsynch, TSM, Universal DBA System DB2 including DB2 Connect and related tools Command, SQL SQL Server Mgmt Studio, Red Gate, The relational database management Vantage, Tivoli, Snap Manager, Toad, system and related tools provided by Enterprise Manager, SQL, Azure SQL SQL Server Microsoft Corp Database The relational database management Oracle enterprise manager, application system and related tools provided by Oracle express, RMAN, PL SQL, SQL developer, ORACLE Corp Toad, SQL The relational database management SYBASE system and related tools provided by Sybase ASE, OEM, RAC, Partioning, Encryption Cincom SUPRA SQL – Cincom's relational database management system provides access to data in open and proprietary environments through industry-standard SQL for standalone and client/server application Supra 2.X solutions. phpadmin, mysqladmin, MySql, Vertica, Open Source Open Source database management system SQLite, Hadoop The hierarchical database management system provided by IBM that runs on z/OS Hierarchical Database IMS mainframe platform including related tools BMC IMS Utilities, Strobe, Omegamon Cincom SUPRA® PDM – Cincom's networked, hierarchical database management system provides access to your data through a Physical Data Manager (PDM) that manages the data structures of the physical files that store the data.
    [Show full text]
  • A Practical Introduction to Python Programming
    A Practical Introduction to Python Programming Brian Heinold Department of Mathematics and Computer Science Mount St. Mary’s University ii ©2012 Brian Heinold Licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported Li- cense Contents I Basics1 1 Getting Started 3 1.1 Installing Python..............................................3 1.2 IDLE......................................................3 1.3 A first program...............................................4 1.4 Typing things in...............................................5 1.5 Getting input.................................................6 1.6 Printing....................................................6 1.7 Variables...................................................7 1.8 Exercises...................................................9 2 For loops 11 2.1 Examples................................................... 11 2.2 The loop variable.............................................. 13 2.3 The range function............................................ 13 2.4 A Trickier Example............................................. 14 2.5 Exercises................................................... 15 3 Numbers 19 3.1 Integers and Decimal Numbers.................................... 19 3.2 Math Operators............................................... 19 3.3 Order of operations............................................ 21 3.4 Random numbers............................................. 21 3.5 Math functions............................................... 21 3.6 Getting
    [Show full text]
  • A Fast-Start Method for Computing the Inverse Tangent
    A Fast-Start Method for Computing the Inverse Tangent Peter Markstein Hewlett-Packard Laboratories 1501 Page Mill Road Palo Alto, CA 94062, U.S.A. [email protected] Abstract duction method is handled out-of-loop because its use is rarely required.) In a search for an algorithm to compute atan(x) For short latency, it is often desirable to use many in- which has both low latency and few floating point in- structions. Different sequences may be optimal over var- structions, an interesting variant of familiar trigonom- ious subdomains of the function, and in each subdomain, etry formulas was discovered that allow the start of ar- instruction level parallelism, such as Estrin’s method of gument reduction to commence before any references to polynomial evaluation [3] reduces latency at the cost of tables stored in memory are needed. Low latency makes additional intermediate calculations. the method suitable for a closed subroutine, and few In searching for an inverse tangent algorithm, an un- floating point operations make the method advantageous usual method was discovered that permits a floating for a software-pipelined implementation. point argument reduction computation to begin at the first cycle, without first examining a table of values. While a table is used, the table access is overlapped with 1Introduction most of the argument reduction, helping to contain la- tency. The table is designed to allow a low degree odd Short latency and high throughput are two conflict- polynomial to complete the approximation. A new ap- ing goals in transcendental function evaluation algo- proach to the logarithm routine [1] which motivated this rithm design.
    [Show full text]
  • Computer Performance Evaluation Users Group (CPEUG)
    COMPUTER SCIENCE & TECHNOLOGY: National Bureau of Standards Library, E-01 Admin. Bidg. OCT 1 1981 19105^1 QC / 00 COMPUTER PERFORMANCE EVALUATION USERS GROUP CPEUG 13th Meeting NBS Special Publication 500-18 U.S. DEPARTMENT OF COMMERCE National Bureau of Standards 3-18 NATIONAL BUREAU OF STANDARDS The National Bureau of Standards^ was established by an act of Congress March 3, 1901. The Bureau's overall goal is to strengthen and advance the Nation's science and technology and facilitate their effective application for public benefit. To this end, the Bureau conducts research and provides: (1) a basis for the Nation's physical measurement system, (2) scientific and technological services for industry and government, (3) a technical basis for equity in trade, and (4) technical services to pro- mote public safety. The Bureau consists of the Institute for Basic Standards, the Institute for Materials Research, the Institute for Applied Technology, the Institute for Computer Sciences and Technology, the Office for Information Programs, and the Office of Experimental Technology Incentives Program. THE INSTITUTE FOR BASIC STANDARDS provides the central basis within the United States of a complete and consist- ent system of physical measurement; coordinates that system with measurement systems of other nations; and furnishes essen- tial services leading to accurate and uniform physical measurements throughout the Nation's scientific community, industry, and commerce. The Institute consists of the Office of Measurement Services, and the following
    [Show full text]
  • Appendix a Mathematical Fundamentals
    Appendix A Mathematical Fundamentals In this book, it is assumed that the reader has familiarity with the mathematical definitions from the areas of Linear Algebra, Trigonometry, and other related areas. Some of them that are introduced in this Appendix to make the reader quickly understand the derivations and notations used in different chapters of this book. A.1 Function ‘Atan2’ The usual inverse tangent function denoted by Atan(z), where z=y/x, returns an angle in the range (-π/2, π/2). In order to express the full range of angles it is useful to define the so called two- argument arctangent function denoted by Atan2(y,x), which returns angle in the entire range, i.e., (- π, π). This function is defined for all (x,y)≠0, and equals the unique angle θ such that x y cosθ = , and sinθ = …(A.1) x 2 + y 2 x 2 + y 2 The function uses the signs of x and y to select the appropriate quadrant for the angle θ, as explained in Table A.1. Table A.1 Evaluation of ‘Atan2’ function x Atan2(y,x) +ve Atan(z) 0 Sgn(y) π/2 -ve Atan(z)+ Sgn(y) π In Table A.1, z=y/x, and Sgn(.) denotes the usual sign function, i.e., its value is -1, 0, or 1 depending on the positive, zero, and negative values of y, respectively. However, if both x and y are zeros, ‘Atan2’ is undefined. Now, using the table, Atan2(-1,1)= -π/4 and Atan2(1,-1)= 3π/4, whereas the Atan(-1) returns -π/4 in both the cases.
    [Show full text]
  • Hardware Implementations of Fixed-Point Atan2
    Hardware Implementations of Fixed-Point Atan2 Hardware Implementations of Fixed-Point Atan2 Florent de Dinechin Matei I¸stoan Universit´ede Lyon, INRIA, INSA-Lyon, CITI-Lab ARITH22 Florent de Dinechin, Matei I¸stoan Hardware Implementations of Fixed-Point Atan2 Hardware Implementations of Fixed-Point Atan2 Introduction: Methods for computing Atan2 Methods for Computing atan2 in Hardware Yet another arithmetic function . • . that is useful in telecom (to recover the phase of a signal) (12{24 bits of precision) • . and in general for cartesian to polar coordinate transformation • and an interesting function, nonetheless 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 1 0.8 1 0.6 0.8 0.4 x 0.6 0.4 0.2 0.2 y 0 0 Florent de Dinechin, Matei I¸stoan Hardware Implementations of Fixed-Point Atan2 ARITH22 2 / 24 Hardware Implementations of Fixed-Point Atan2 Introduction: Methods for computing Atan2 Common Specification • target function y 1 (x; y) 1 y α = atan2(y; x) f (x; y) = arctan ( ) π x −1 1 x • input: fixed-point format −1 −1 0 1 ky y arctan ( ) = arctan ( ) [ ) kx x • output: fixed-point format and binary angles y (0; 1) π 2 −1 0 1 (−1; 0) π 0 (1; 0) −π x =) [ ) Florent de Dinechin, Matei I¸stoan Hardware Implementations of Fixed-Point Atan2 ARITH22 3 / 24 Hardware Implementations of Fixed-Point Atan2 Introduction: Methods for computing Atan2 Common Specification • target function y 1 (x; y) 1 y α = atan2(y; x) f (x; y) = arctan ( ) π x −1 1 x • input: fixed-point format −1 −1 0 1 ky y arctan ( ) = arctan ( ) [ ) kx x • output: fixed-point format and binary
    [Show full text]