Geospatially-Intelligent Three-Dimensional Multivariate
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
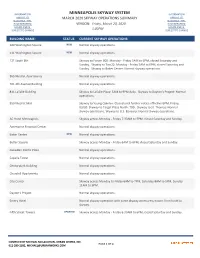
REPORTED VERSION: Friday, March 20, 2020 HAVE REPORTED HOURS and IS HOURS and IS SUBJECT to CHANGE 5:00PM SUBJECT to CHANGE
INFORMATION MINNEAPOLIS SKYWAY SYSTEM INFORMATION LIMITED TO MARCH 2020 SKYWAY OPERATIONS SUMMARY LIMITED TO BUILDINGS THAT BUILDINGS THAT HAVE REPORTED VERSION: Friday, March 20, 2020 HAVE REPORTED HOURS AND IS HOURS AND IS SUBJECT TO CHANGE 5:00PM SUBJECT TO CHANGE BUILDING NAME: STATUS CURRENT SKYWAY OPERATIONS: 100 Washington SquareNEW Normal skyway operations. 111 Washington SquareNEW Normal skyway operations. 121 South 8th Skyway to Forum 900: Monday ‐ Friday 5AM to 6PM, closed Saturday and Sunday. Skyway to Two22: Monday ‐ Friday 5AM to 6PM, closed Saturday and Sunday. Skyway to Baker Center: Normal skyway operations. 365 Nicollet Apartments Normal skyway operations. 701 4th Avenue Building Normal skyway operations. 811 LaSalle Building Skyway to LaSalle Plaza: 5AM to 9PM daily. Skyway to Dayton's Project: Normal operations. 950 Nicollet Mall Skyway to Young Quinlan: Closed until further notice effective 6PM, Friday, 03/20. Skyway to Target Plaza North: TBD. Skyway to St. Thomas: Normal skyway operations. Skyway to U.S. Bancorp: Normal skyway operations. AC Hotel Minneapolis Skyway access Monday ‐ Friday 7:30AM to 5PM, closed Saturday and Sunday. Ameriprise Financial Center Normal skyway operations. Baker CenterNEW Normal skyway operations. Butler Square Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. Canadian Pacific Plaza Normal skyway operations. Capella Tower Normal skyway operations. CenturyLink Building Normal skyway operations. Churchill Apartments Normal skyway operations. City Center Skyway access Monday to Friday 6AM to 7PM, Saturday 8AM to 5PM, Sunday 11AM to 5PM. Dayton's Project Normal skyway operations. Emery Hotel Normal skyway operation with some skyway access restrictions from hotel to skyway. -

Buildings & Parking) (Ft²
Total Floor Weather Weather Total GHG ENERGY Source Water Primary Area Site EUI Normalized Normalized Emissions Property Name Address STAR EUI Use Property Type (Buildings & (kBtu/ft²) Site EUI Source EUI (Metric Tons Score (kBtu/ft²) (kgal) Parking) (ft²) (kBtu/ft²) (kBtu/ft²) CO2e) DeLaSalle High School 1 DeLaSalle Dr 84 K-12 School 217,000 63.6 61 95.1 92.5 2790 808 Riverplace - One Main 1 Main Street SE 96 Office 97,551 23.5 23.4 65.1 65.1 449.8 375.9 Other - Twins Ballpark LLC 1 Twins Way N/A Entertainment/ 1,311,792 82.6 82.2 186.4 185.9 16204.4 12251.5 Public Assembly Riverplace - East 10 NE 2nd Street 16 Office 87,703 145.3 139 270 263.5 3501.5 1340.4 Bridge 3405 10 W Lake Street 91 Retail Store 91,805 42.2 40 89.8 86.2 397 474.6 Butler Square 100 6th St North 86 Office 457,678 52.4 51.1 108.4 106.5 2647 2846.9 Fifth Street Towers 100 South 5th Street 85 Office 1,420,153 58.3 56.7 131.5 129.9 4901.3 8921.7 100 Washington 100 Washington Ave 84 Office 770,894 62.6 61 128.3 126.6 6474.6 4720.6 Square S College/ TMH 1000 LaSalle Avenue N/A 165,516 71.1 69.5 141.2 139.3 2088.4 1352.8 University Target Plaza 1000 Nicollet Mall 87 Office 2,042,785 68.7 67.7 127.9 126.6 11990 14098.6 DCI 1001 Minneapolis 1001 3rd Avenue 69 Office 541,542 87.6 86 175.5 173.8 4243.8 4428.7 Venture LLC South Other - St Joseph's Home for 1001 46th St E N/A Lodging/ 123,821 115.4 112.3 176.5 173.2 1306.8 1199.8 Children Residential Hilton Minneapolis 1001 S Marquette 49 Hotel 781,000 122.1 120.9 210.1 208.9 38618.9 9186.1 (MSPMH) Ave Total Floor Weather Weather -

Minneapolis Skyway System
INFORMATION MINNEAPOLIS SKYWAY SYSTEM INFORMATION LIMITED TO SKYWAY OPERATIONS SUMMARY LIMITED TO BUILDINGS THAT BUILDINGS THAT HAVE REPORTED VERSION: Friday, June 26, 2020 HAVE REPORTED HOURS AND IS HOURS AND IS SUBJECT TO CHANGE 2:30PM SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Normal skyway operations. 111 Washington Square Normal skyway operations. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access to Bolero Flats only. Hall Ramp) 11th Street Underground Ramp Skyway access closed until further notice. 121 South 8th Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. 330 South Second Building Normal skyway operations. 365 Nicollet Apartments Skyway access closed until further notice. 510 Marquette Skyway access closed until further notice. 517 Marquette Ramp Normal skyway operations. 5th Avenue Parking Ramp Skyway access closed until further notice. 701 4th Avenue Building Skyway access closed until further notice. 811 LaSalle Building Skyway to LaSalle Plaza: 6AM to 10PM daily. Skyway to Dayton's Project: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday 950 Nicollet MallUPDATED Skyway to Young Quinlan: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. Skyway to Target Plaza North: Closed until June 29th. Skyway to St. Thomas: Closed until further notice. Skyway to U.S. Bancorp: Monday ‐ Friday, 6AM to 6PM, closed Saturday and Sunday. AC Hotel Minneapolis Skyway access Monday ‐ Friday 7:30AM to 5PM, closed Saturday and Sunday. Ameriprise Financial Center Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. Baker Center Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. -

REPORTED VERSION: Tuesday, March 24, 2020 HAVE REPORTED HOURS and IS HOURS and IS SUBJECT to CHANGE 3PM SUBJECT to CHANGE
INFORMATION MINNEAPOLIS SKYWAY SYSTEM INFORMATION LIMITED TO MARCH 2020 SKYWAY OPERATIONS SUMMARY LIMITED TO BUILDINGS THAT BUILDINGS THAT HAVE REPORTED VERSION: Tuesday, March 24, 2020 HAVE REPORTED HOURS AND IS HOURS AND IS SUBJECT TO CHANGE 3PM SUBJECT TO CHANGE BUILDING NAME: STATUS CURRENT SKYWAY OPERATIONS: 100 Washington Square Normal skyway operations. 111 Washington Square Normal skyway operations. 121 South 8th Skyway to Forum 900: Monday ‐ Friday 5AM to 6PM, closed Saturday and Sunday. Skyway to Two22: Monday ‐ Friday 5AM to 6PM, closed Saturday and Sunday. Skyway to Baker Center: Normal skyway operations. 365 Nicollet ApartmentsUPDATED Skyway access closed until further notice. 701 4th Avenue Building Normal skyway operations. 811 LaSalle Building Skyway to LaSalle Plaza: 5AM to 9PM daily. Skyway to Dayton's Project: Normal operations. 950 Nicollet Mall Skyway to Young Quinlan: Closed until further notice effective 6PM, Friday, 03/20. Skyway to Target Plaza North: TBD. Skyway to St. Thomas: Normal skyway operations. Skyway to U.S. Bancorp: Normal skyway operations. AC Hotel Minneapolis Skyway access Monday ‐ Friday 7:30AM to 5PM, closed Saturday and Sunday. Ameriprise Financial Center Normal skyway operations. Baker Center Normal skyway operations. Butler Square Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. Canadian Pacific Plaza Normal skyway operations. Capella Tower Normal skyway operations. CenturyLink Building Normal skyway operations. Churchill Apartments Normal skyway operations. City Center Skyway access Monday to Friday 6AM to 6PM, Saturday 8AM to 5PM, closed Sunday. Dayton's Project Normal skyway operations. Edition Apartments Normal skyway operations. Emery Hotel Skyway access Monday ‐ Friday 7AM ‐ 2:30PM, closed Saturday and Sunday. -
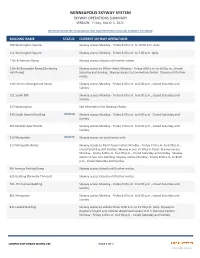
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Friday, March 5, 2021
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Friday, March 5, 2021 INFORMATION LIMITED TO BUILDINGS THAT HAVE REPORTED HOURS AND IS SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 10:00 p.m. daily. 111 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 7:00 p.m. daily. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access to Hilton Hotel: Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Hall Ramp) Saturday and Sunday. Skyway access to Convention Center: Closed until further notice. 11th Street Underground Ramp Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 121 South 8th Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 323 Washington See information for Gateway Ramp. 330 South Second BuildingUPDATED Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m. Closed Saturday and Sunday. 365 Nicollet Apartments Skyway access Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 510 MarquetteUPDATED Skyway access via card access only. 517 Marquette Ramp Skyway access to Rand Tower Hotel: Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. Skyway access to Westin Hotel: Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. Skyway access to Soo Line Building: Skyway access Monday ‐ Friday 6:00 a.m. -

MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Thursday, February 18, 2021
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Thursday, February 18, 2021 INFORMATION LIMITED TO BUILDINGS THAT HAVE REPORTED HOURS AND IS SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 10:00 p.m. daily. 111 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 7:00 p.m. daily. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access to Hilton Hotel: Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Hall Ramp) Saturday and Sunday. Skyway access to Convention Center: Closed until further notice. 11th Street Underground Ramp Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 121 South 8th Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 323 WashingtonUPDATED See information for Gateway Ramp. 330 South Second Building Skyway access Monday ‐ Friday 6:00 a.m. to 10:00 p.m., Saturday 9:30 a.m. to 8:00 p.m., Sunday 12:00 p.m. to 6:00 p.m. 365 Nicollet Apartments Skyway access Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 510 Marquette Skyway access closed until further notice. 517 Marquette Ramp Skyway access to Rand Tower Hotel: Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. Skyway access to Westin Hotel: Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. -

Eligible Multifamily Residential Building List for Reporting Year 2020
Eligible Multifamily Residential Building List for Reporting Year 2020 This data is sorted by "Building Address" *Please note: If there is an empty value under the "Property Name" field, it means that we didn't receive 2019 energy use data Property Name Building Address Total Building Area Winslow House 100 2ND St SE Minneapolis, MN 55414 102924 Village Lofts at St. Anthony 100 2ND St NE Minneapolis, MN 55414 The Carlyle 100 3RD Ave S Minneapolis, MN 55401 382989 100 3rd Ave SE Minneapolis, MN 55414 53898 Diamond Lake Properties 100 Diamond Lake Rd W Minneapolis, MN 55419 70375 Maverick Greystar 120 Hennepin Ave Minneapolis, MN 55401 204825 Belmont Apartments 1000 Franklin Ave W Minneapolis, MN 55404 68800 FloCo Fusion 1000 University Ave SE Minneapolis, MN 55414 100673 St Joseph's Home for Children 1001 46TH St E Minneapolis, MN 55407 123821 Buzza Lofts (510) 1006 Lake St W Minneapolis, MN 55408 113883 308 - University Commons 101 27th Ave SE Minneapolis, MN 55414 189776 Soo Line Building City Apartments 101 5TH St S Minneapolis, MN 55402 250000 1015 8th St SE Minneapolis, MN 55414 72810 Wahu 1016 Washington Ave SE Minneapolis, MN 55414 681251 Augustana Apartments 1020 17TH St E Minneapolis, MN 55404 156797 Churchill Apartments - ch53 111 Marquette Ave Minneapolis, MN 55401 522282 Abbott Apartments 110 18TH St E Minneapolis, MN 55403 130949 La Rive 110 Bank St Minneapolis, MN 55414 192356 OneTen Grant Apartments 110 Grant St W Minneapolis, MN 55403 413280 East Village North: East Village North 1105 8th St S Minneapolis, MN 55404 79210 -
REPORTED VERSION: Thursday, March 26, 2020 HAVE REPORTED HOURS and IS HOURS and IS SUBJECT to CHANGE 4PM SUBJECT to CHANGE
INFORMATION MINNEAPOLIS SKYWAY SYSTEM INFORMATION LIMITED TO MARCH 2020 SKYWAY OPERATIONS SUMMARY LIMITED TO BUILDINGS THAT BUILDINGS THAT HAVE REPORTED VERSION: Thursday, March 26, 2020 HAVE REPORTED HOURS AND IS HOURS AND IS SUBJECT TO CHANGE 4PM SUBJECT TO CHANGE BUILDING NAME: STATUS CURRENT SKYWAY OPERATIONS: 100 Washington SquareUPDATED Skyway access to be closed until further notice effective 5PM, Friday, March 27. 111 Washington SquareUPDATED Skyway access to be closed until further notice effective 5PM, Friday, March 27. 11th & Harmon RampNEW Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra NEW Skyway access 6AM to 6PM daily. Hall Ramp) 121 South 8th Skyway access to be closed until further notice effective 6PM, Friday, March 27. 330 South Second BuildingNEW Skyway access to be closed for two weeks effective the evening of Friday, March 27. 365 Nicollet Apartments Skyway access closed until further notice. 510 MarquetteUPDATED Skyway access closed until further notice. 701 4th Avenue Building Normal skyway operations. 811 LaSalle BuildingUPDATED Skyway to LaSalle Plaza: 6AM to 6PM daily. Skyway to Dayton's Project: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday 950 Nicollet MallUPDATED Skyway to Young Quinlan: Closed until further notice effective 6PM, Friday, 03/20. Skyway to Target Plaza North: TBD. Skyway to St. Thomas: Normal skyway operations. Skyway to U.S. Bancorp: Monday ‐ Friday, 6AM to 8PM, Saturday 10AM to 8PM, Sunday 12PM to 8PM. AC Hotel Minneapolis Skyway access Monday ‐ Friday 7:30AM to 5PM, closed Saturday and Sunday. Ameriprise Financial Center Normal skyway operations. Baker Center Normal skyway operations. Butler SquareUPDATED Skyway access will be closed through April 12th effective Friday, March 27. -
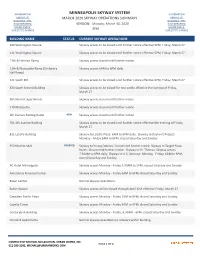
REPORTED VERSION: Monday, March 30, 2020 HAVE REPORTED HOURS and IS HOURS and IS SUBJECT to CHANGE 3PM SUBJECT to CHANGE
INFORMATION MINNEAPOLIS SKYWAY SYSTEM INFORMATION LIMITED TO MARCH 2020 SKYWAY OPERATIONS SUMMARY LIMITED TO BUILDINGS THAT BUILDINGS THAT HAVE REPORTED VERSION: Monday, March 30, 2020 HAVE REPORTED HOURS AND IS HOURS AND IS SUBJECT TO CHANGE 3PM SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Skyway access to be closed until further notice effective 5PM, Friday, March 27. 111 Washington Square Skyway access to be closed until further notice effective 5PM, Friday, March 27. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access 6AM to 6PM daily. Hall Ramp) 121 South 8th Skyway access to be closed until further notice effective 6PM, Friday, March 27. 330 South Second Building Skyway access to be closed for two weeks effective the evening of Friday, March 27. 365 Nicollet Apartments Skyway access closed until further notice. 510 Marquette Skyway access closed until further notice. 5th Avenue Parking RampNEW Skyway access closed until further notice. 701 4th Avenue Building Skyway access to be closed until further notice effective the evening of Friday, March 27. 811 LaSalle Building Skyway to LaSalle Plaza: 6AM to 6PM daily. Skyway to Dayton's Project: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday 950 Nicollet MallUPDATED Skyway to Young Quinlan: Closed until further notice. Skyway to Target Plaza North: Closed until further notice. Skyway to St. Thomas: Skyway access 7:30AM to 6PM daily. Skyway to U.S. Bancorp: Monday ‐ Friday, 6AM to 6PM, closed Saturday and Sunday. AC Hotel Minneapolis Skyway access Monday ‐ Friday 7:30AM to 5PM, closed Saturday and Sunday. -
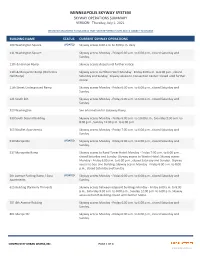
SKYWAY OPERATIONS SUMMARY VERSION: Thursday, July 1, 2021
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Thursday, July 1, 2021 INFORMATION LIMITED TO BUILDINGS THAT HAVE REPORTED HOURS AND IS SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington SquareUPDATED Skyway access 6:00 a.m. to 6:00 p.m. daily 111 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access to Hilton Hotel: Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Hall Ramp) Saturday and Sunday. Skyway access to Convention Center: Closed until further notice. 11th Street Underground Ramp Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 121 South 8th Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 323 Washington See information for Gateway Ramp. 330 South Second Building Skyway access Monday ‐ Friday 6:00 a.m. to 10:00 p.m., Saturday 9:30 a.m. to 8:00 p.m., Sunday 12:00 p.m. to 6:00 p.m. 365 Nicollet Apartments Skyway access Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 510 MarquetteUPDATED Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 517 Marquette Ramp Skyway access to Rand Tower Hotel: Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. Skyway access to Westin Hotel: Skyway access Monday ‐ Friday 6:00 a.m. -
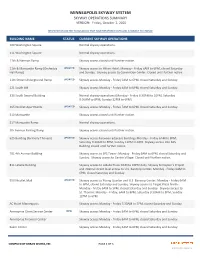
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Friday, October 2, 2020
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Friday, October 2, 2020 INFORMATION LIMITED TO BUILDINGS THAT HAVE REPORTED HOURS AND IS SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Normal skyway operations. 111 Washington Square Normal skyway operations. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra UPDATED Skyway access to Hilton Hotel: Monday ‐ Friday 6AM to 6PM, closed Saturday Hall Ramp) and Sunday. Skyway access to Convention Center: Closed until further notice. 11th Street Underground RampUPDATED Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. 121 South 8th Skyway access Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. 330 South Second Building Normal skyway operations (Monday ‐ Friday 6:30AM to 10PM, Saturday 9:30AM to 8PM, Sunday 12PM to 6PM). 365 Nicollet ApartmentsUPDATED Skyway access Monday ‐ Friday 7AM to 6PM, closed Saturday and Sunday. 510 Marquette Skyway access closed until further notice. 517 Marquette Ramp Normal skyway operations. 5th Avenue Parking Ramp Skyway access closed until further notice. 625 Building (formerly Thrivent)UPDATED Skyway access between adjacent buildings Monday ‐ Friday 6AM to 8PM, Saturday 9:30AM to 8PM, Sunday 12PM to 6PM. Skyway access into 625 Building closed until further notice. 701 4th Avenue Building Skyway access to SPS Tower: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. Skyway access to Centre Village: Closed until further notice. 811 LaSalle Building Skyway access to LaSalle Plaza: 6AM to 10PM daily. Skyway to Dayton's Project and internal street level access to U.S. Bancorp Center: Monday ‐ Friday 6AM to 6PM, closed Saturday and Sunday. -
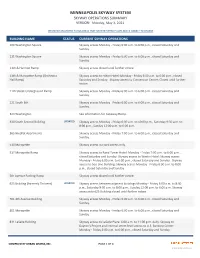
SKYWAY OPERATIONS SUMMARY VERSION: Monday, May 3, 2021
MINNEAPOLIS SKYWAY SYSTEM SKYWAY OPERATIONS SUMMARY VERSION: Monday, May 3, 2021 INFORMATION LIMITED TO BUILDINGS THAT HAVE REPORTED HOURS AND IS SUBJECT TO CHANGE BUILDING NAME STATUS CURRENT SKYWAY OPERATIONS 100 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 111 Washington Square Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 11th & Harmon Ramp Skyway access closed until further notice. 11th & Marquette Ramp (Orchestra Skyway access to Hilton Hotel: Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Hall Ramp) Saturday and Sunday. Skyway access to Convention Center: Closed until further notice. 11th Street Underground Ramp Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 121 South 8th Skyway access Monday ‐ Friday 6:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 323 Washington See information for Gateway Ramp. 330 South Second BuildingUPDATED Skyway access Monday ‐ Friday 6:00 a.m. to 10:00 p.m., Saturday 9:30 a.m. to 8:00 p.m., Sunday 12:00 p.m. to 6:00 p.m. 365 Nicollet Apartments Skyway access Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. 510 Marquette Skyway access via card access only. 517 Marquette Ramp Skyway access to Rand Tower Hotel: Monday ‐ Friday 7:00 a.m. to 6:00 p.m., closed Saturday and Sunday. Skyway access to Westin Hotel: Skyway access Monday ‐ Friday 6:00 a.m.